专题9圆—9.2圆心圆周角度-2021年鲁教版(五四制)九年级数学专题复习训练(word版含答案)
文档属性
| 名称 | 专题9圆—9.2圆心圆周角度-2021年鲁教版(五四制)九年级数学专题复习训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 07:17:43 | ||
图片预览



文档简介
圆周角
【知识点梳理】
①圆心角与圆周角的关系: 同圆或等圆中,同弧或等弧所对的圆周角等于它所对的国心角的一半.
②圆内接四边形:顶点都在国上的四边形,叫圆内接四边形.圆内接四边形对角互补(巧用).
③圆周角定理:直径所对的圆周角是直角,反过来,90°的圆周角所对的弦是直径;如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
④圆既是轴对称图形又是中心对称图形
圆周角与圆心角关系
【经典例题1】如图,AB是☉O的直径,点C是半径OA的中点,过点C作AB的垂线,交☉O于点D,E两点,过点D作直径DF,连接AF,则∠DFA=____.?
【解析】∵点C是半径OA的中点,∴OC=OD,
∵DE⊥AB,∴∠CDO=30°,
∴∠DOA=60°,∴∠DFA=30°,
【经典例题2】如图,AB为☉O的直径,点P为其半圆上任意一点(不含A,B两点),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,求y与x的函数关系式.
【解析】解答
∵∠BOP=2∠BQP=2y°,
∵AB为⊙O的直径,
∴∠AOP+∠BOP=180°,
∴x+2y=180,
∴y=90?x,且0【经典例题3】如图,一块含45°角的直角三角板,它的一个锐角顶点A在☉O上,边AB,AC分别与☉O交于点D,E,则∠DOE的度数为___.?
【解析】∵∠A=45°,
∴∠DOE=2∠A=90°.
故答案为:90°.
练习2-1如图,四边形ABCD内接于☉O,若四边形OABC是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
练习2-2如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 ?,那么∠B= ?.
练习2-3(毕节中考)如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
A.30° B.50° C.60° D.70°
练习2-4(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
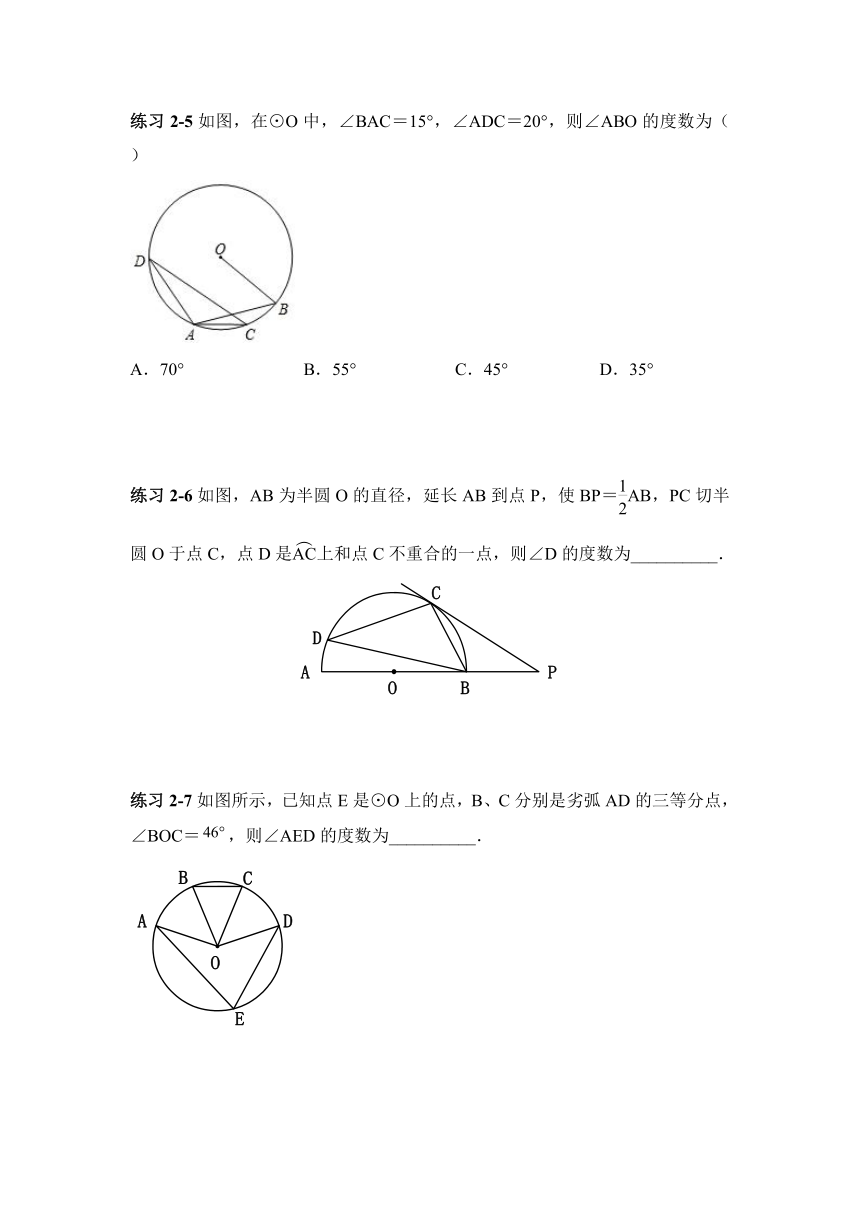
练习2-5如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为()
A.70° B.55° C.45° D.35°
练习2-6如图,AB为半圆O的直径,延长AB到点P,使BP=AB,PC切半圆O于点C,点D是上和点C不重合的一点,则∠D的度数为__________.
练习2-7如图所示,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=,则∠AED的度数为__________.
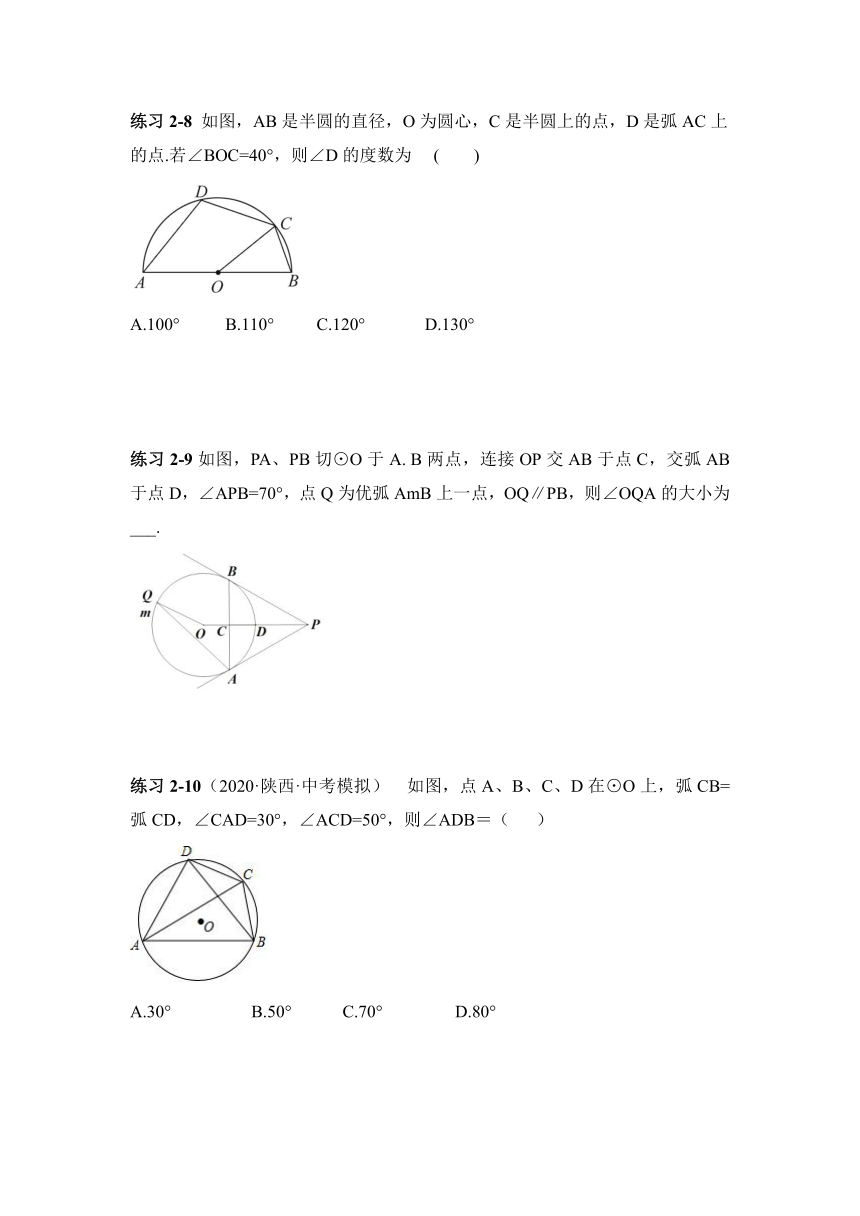
练习2-8 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点.若∠BOC=40°,则∠D的度数为 ( )
A.100° B.110° C.120° D.130°
练习2-9如图,PA、PB切⊙O于A. B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为___.
练习2-10(2020·陕西·中考模拟) 如图,点A、B、C、D在⊙O上,弧CB=弧CD,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
练习2-11如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与 AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
练习2-12如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止。设∠POF=x°,则x的取值范围是( )
A. 30?x?60 B. 30?x?90 C. 30?x?120 D. 60?x?120
练习2-13如图,四边形 ABCD 是菱形,⊙O 经过点 A、C、D,与 BC 相交于点 E,连接 AC、AE.若∠D=80°,则∠EAC 的度数为( )
A.20° B.35° C.40° D.55°
练习2-14如图,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是 ( )
A.15° B.30° C.45° D.60°
练习2-15如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为 .
练习2-16如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC= .
练习2-17如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为 .
练习2-18如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD= .
练习2-19如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
练习2-20如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
【经典例题3】如图,点A是量角器直径的一个端点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ.若点P对应135°(45°),则∠PQB的度数为( )
A.65° B.67.5° C.60° D.80°
【解析】连接OP,如图,则∠AOP=135°,
∴∠ABP=12∠AOP=67.5°.
∵PB=PQ,
∴∠PQB=∠ABP=67.5°.
故选:B.
练习3-1如图所示,量角器外缘边上有A、P、Q三点,它们所表示的读数分别是180°,,30°,则∠PAQ的大小为( )
A.10° B.20° C.30° D.40°
练习3-2如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C旋转,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是 .
练习3-3将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
练习3-4如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 .
题型四:与圆结合,利用圆的基本性质进行转化求解
【经典例题4】(攀枝花中考)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
练习4-1如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A. B. C.2 D.
练习4-2如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为_____.
练习4-3如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B. C. D.
练习4-4【转化思想】如图,求∠1的正切值.
练习4-5某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
A. B. C. D.
练习4-6(20年烟台一模)某数学研究性学习小组制作了如下的三角函数计算图尺来测量0°—90°的三角函数值:在一个圆心角为90°的扇形OAB中,以OB为直径在扇形内部画半圆M,将一根笔直的、长度等于OB的细木条分成10等份,并标上0到10刻度,将木条0刻度端点与点O重合,另一端点C落在圆弧AB上,木条OC与半圆M交点D.设∠AOC的度数是α,则通过读取点D处木条上的刻度可以( )
A.读取sinα的值,结果最小保留到百分位
B.读取sinα的值,结果最小保留到十分位
C.读取cosα的值,结果最小保留到百分位
D.读取cosα的值,结果最小保留到十分位
参考答案:
练习2-1如图,四边形ABCD内接于☉O,若四边形OABC是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
【解析】设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
练习2-2如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 ?,那么∠B= ?.
【解析】连接DE、CE,则∠2=θ,∠5=∠6=2θ,
∵∠6是△BDE的外角,
∴∠6=∠2+∠ABC=2θ,
∵∠5+∠6+∠1=180°,
∴4θ+∠1=180°①,
在△ACE中,
∵AE=CE,
∴∠3=∠CAE=63°,
∴∠4=180°?∠3?∠CAE=180°?63°?63°=54°,
∵∠4+∠1+∠2=180°,即54°+∠1+θ=180°②,
①②联立得,θ=18°.
故答案为:18°.
练习2-3(毕节中考)如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
A.30° B.50° C.60° D.70°
【解析】∵∠ACD=30°,
∴∠ABD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD=90°-∠ABD=60°.
故选C.
练习2-4(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
【解析】∵连接OC,
∵△ABC内接于⊙O,∠A=α,
∴∠BOC=2∠A=2α,
∵OB=OC,
∴∠OBC=∠OCB==90°.
故选D.
练习2-5如图,在⊙O 中,∠BAC=15°,∠ADC=20°,则∠ABO 的度数为( )
A.70° B.55° C.45° D.35°
【解析】连接OA、OC,
∵∠BAC=15°,∠ADC=20°,
∴∠AOB=2(∠ADC+∠BAC)=70°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°?∠AOB)=55°.
故选:B.
练习2-6如图,AB为半圆O的直径,延长AB到点P,使BP=AB,PC切半圆O于点C,点D是上和点C不重合的一点,则∠D的度数为__________.
【解析】
连接OC,
∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB=∠COP=30°.
练习2-7如图所示,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=,则∠AED的度数为__________.
【解析】∵B、C分别是劣弧AD的三等分点,∠BOC=46°,
∴∠AOD=138°,
∴∠AED=138°÷2=69°.
练习2-8 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点.若∠BOC=40°,则∠D的度数为 ( )
A.100° B.110° C.120° D.130°
【解析】∴∠AOC=180°?40°=140°,
∴∠D=12×(360°?140°)=110°,
故选:B.
练习2-9如图,PA、PB切⊙O于A. B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为___.
【解析】如图,连接OA.
∵PA,PB是⊙O的切线,
∴∠OPB=∠OPA=12∠APB=35°,PA⊥OA,
∴∠OAP=90°,
∴∠POA=90°?35°=55°,
∵OQ∥PB,
∴∠POQ=180°?∠OPB=145°,
∴∠AOQ=360°?145°?55°=160°,
∵OQ=OA,
∴∠OQA=∠OAQ=12(180°?∠AOQ)=10°,
故答案为10°.
练习2-10(2020·陕西·中考模拟) 如图,点A、B、C、D在⊙O上,弧CB=弧CD,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
【解析】弧CB=弧CD,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°?∠CAB?∠ABC=180°?50°?30°?30°=70°.
故选:C.
练习2-11如图,AB 是⊙O 的直径,EF,EB 是⊙O 的弦,且 EF=EB,EF 与 AB 交于点 C, 连接 OF,若∠AOF=40°,则∠F 的度数是( )
【解析】连接FB.
∵∠AOF=40°,
∴∠FOB=180°?40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∴∠EFO=∠EFB?∠OFB=35°,
故答案为:35°.
练习2-12如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止。设∠POF=x°,则x的取值范围是( )
A. 30?x?60 B. 30?x?90 C. 30?x?120 D. 60?x?120
【解析】开始移动时,x=30°,
移动开始后,∠POF逐渐增大,
最后当B与E重合时,∠POF取得最大值,
则根据同弧所对的圆心角等于它所对圆周角的2倍得:
∠POF=2∠ABC=2×30°=60°,
故x的取值范围是30?x?60.
故选A.
练习2-13如图,四边形 ABCD 是菱形,⊙O 经过点 A、C、D,与 BC 相交于点 E,连接 AC、AE.若∠D=80°,则∠EAC 的度数为( )
A.20° B.35° C.40° D.55°
【解析】四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°?∠D)=50°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB?∠ACE=30°,
故选:C.
练习2-14如图,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是 ( B )
A.15° B.30° C.45° D.60°
【解析】由题意得∠COD=90°,
∵D(0,1),C(,0),
∴OD=1,OC=,
∴CD=,
勾股定理
∴∠OCD=30°,
含30度角的直角三角形的判定
∴∠OBD=∠OCD=30°.
同弧或等弧所对的圆周角相等
故选B.
练习2-15如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为 .
【解析】连接OA,
∵OA=OB,∠ABO=40°,
∴∠OAB=∠ABO=40°,
∵∠BCD=112°,
∴∠BAD=180°﹣∠BCD=68°,
∴∠OAE=∠BAD﹣∠OAB=28°,
∵OA=OD,
∴∠ODA=∠OAD=28°
∵E是AD中点,
∴OE⊥AD,
∴∠DOE=90°﹣∠ODA=62°.
故答案为:62°.
练习2-16如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC= .
【解析】连接BD,
∵弦DC⊥BC,
∴∠BCD=90°,
∴BD是直径,
∵⊙O的半径为5cm,弦BC长为6cm,
∴BD=10cm,
∴CD==8cm,
∴tan∠BAC=tan∠BDC===.
故答案为:.
练习2-17如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为 .
【解析】∵∠ACB为△ACE的外角,
∴∠ACE=∠A+∠AEC
∵,∠AEC=37°,∠CAE=31°,
∴∠ACE=68°.
由圆周角定理,得∠ADB=∠ACB,
∴∠ADB=68°,
∴∠APB=∠A+∠ADB=31°+68°=99°,
故答案为99°.
练习2-18如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD= .
【解析】∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=90°﹣∠ABD=90°﹣54°=36°,
∴∠BCD=∠A=36°,
故答案为36°.
练习2-19如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
【解析】连接OC,OD,
∵∠BAO=∠CBO=∠DCO=∠EDO=α,
∵OA=OB=OC,
∴∠ABO=∠BCO=α,
∴∠AOB=∠BOC=∠COD=∠DOE=180°﹣2α,
∴4∠AOB+∠AOE=360°,
∴∠AOB=76°,
∴在等腰三角形AOB中,
∠α=∠BAO==52°.
故选:A.
练习2-20如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
【解析】∵的度数是40°,
∴∠ACM=40°
∵∠CBP=∠CAP=10°,
∴A、C、P、B四点共圆,
∴∠ACM=∠ABP=40°,
∵∠CPB=10°,
∴∠ABC=40°﹣10°=30°,
∵AC=BC,
∴∠CAB=∠ABC=30°,
∴∠ACB=120°,
∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,
∴的度数是20°.
故选:C.
【经典例题3】如图,点A是量角器直径的一个端点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ.若点P对应135°(45°),则∠PQB的度数为( )
A.65° B.67.5° C.60° D.80°
【解析】连接OP,如图,则∠AOP=135°,
∴∠ABP=12∠AOP=67.5°.
∵PB=PQ,
∴∠PQB=∠ABP=67.5°.
故选:B.
练习3-1如图所示,量角器外缘边上有A、P、Q三点,它们所表示的读数分别是180°,,30°,则∠PAQ的大小为( )
A.10° B.20° C.30° D.40°
【解析】设量角器的圆心角为O,连接PO,QO,
知∠POQ=70°-30°=40°,
而∠PAQ为所对的圆周角,
为∠POQ的一半,
所以∠PAQ=∠POQ=×40°=20°.
练习3-2如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C旋转,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是 .
【解析】①设CD′交AB于E,设AB的中点为O,连接OD′当EB=EC,此时∠EBC=∠ECB=40°,易知∠BOD′=2∠BCD′=80°,
∴点D′在量角器上对应的度数是80°;
②设CD″交AB于F,连接OD″,当BF=BC时,∠BCD″=70°,
易知∠BOD″=2∠BCD″=140°,
∴点D″在量角器上对应的度数是140°;
故答案为80°或140°
练习3-3将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
【解析】设半圆圆心为O,连OA,OB,如图,
∵∠ACB=∠AOB,
而∠AOB=86°﹣30°=56°,
∴∠ACB=×56°=28°.
故答案为:28°.
练习3-4如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 .
【解析】∵一块直角三角板ABC的斜边AB与量角器的直径重合,
∴点A、B、C、D都在以AB为直径的圆上,
∵点D对应54°,即∠AOD=54°,
∴∠ACD=∠AOD=27°,
∴∠BCD=90°﹣∠ACD=63°.
故答案为:63°.
题型四:与圆结合,利用圆的基本性质进行转化求解
【经典例题4】(攀枝花中考)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
练习4-1如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A. B. C.2 D.
练习4-2如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为_____.
练习4-3如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B. C. D.
练习4-4【转化思想】如图,求∠1的正切值.
练习4-5某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
A. B. C. D.
练习4-6(20年烟台一模)某数学研究性学习小组制作了如下的三角函数计算图尺来测量0°—90°的三角函数值:在一个圆心角为90°的扇形OAB中,以OB为直径在扇形内部画半圆M,将一根笔直的、长度等于OB的细木条分成10等份,并标上0到10刻度,将木条0刻度端点与点O重合,另一端点C落在圆弧AB上,木条OC与半圆M交点D.设∠AOC的度数是α,则通过读取点D处木条上的刻度可以( )
A.读取sinα的值,结果最小保留到百分位
B.读取sinα的值,结果最小保留到十分位
C.读取cosα的值,结果最小保留到百分位
D.读取cosα的值,结果最小保留到十分位
练习4-7如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧上的一点,则tan∠APB的值是( ).
A.1 B. C. D.
练习4-8(20年济宁中考)如图,是正方形ABCD的内切圆,切点分别为E、F、G、H,ED与相交于点M,则sin∠MFG的值为 .
【经典例题4】D
练习4-1 、、C、、D、A、A
练习4-8 【提示】连接EG。
【知识点梳理】
①圆心角与圆周角的关系: 同圆或等圆中,同弧或等弧所对的圆周角等于它所对的国心角的一半.
②圆内接四边形:顶点都在国上的四边形,叫圆内接四边形.圆内接四边形对角互补(巧用).
③圆周角定理:直径所对的圆周角是直角,反过来,90°的圆周角所对的弦是直径;如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
④圆既是轴对称图形又是中心对称图形
圆周角与圆心角关系
【经典例题1】如图,AB是☉O的直径,点C是半径OA的中点,过点C作AB的垂线,交☉O于点D,E两点,过点D作直径DF,连接AF,则∠DFA=____.?
【解析】∵点C是半径OA的中点,∴OC=OD,
∵DE⊥AB,∴∠CDO=30°,
∴∠DOA=60°,∴∠DFA=30°,
【经典例题2】如图,AB为☉O的直径,点P为其半圆上任意一点(不含A,B两点),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,求y与x的函数关系式.
【解析】解答
∵∠BOP=2∠BQP=2y°,
∵AB为⊙O的直径,
∴∠AOP+∠BOP=180°,
∴x+2y=180,
∴y=90?x,且0
【解析】∵∠A=45°,
∴∠DOE=2∠A=90°.
故答案为:90°.
练习2-1如图,四边形ABCD内接于☉O,若四边形OABC是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
练习2-2如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 ?,那么∠B= ?.
练习2-3(毕节中考)如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
A.30° B.50° C.60° D.70°
练习2-4(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
练习2-5如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为()
A.70° B.55° C.45° D.35°
练习2-6如图,AB为半圆O的直径,延长AB到点P,使BP=AB,PC切半圆O于点C,点D是上和点C不重合的一点,则∠D的度数为__________.
练习2-7如图所示,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=,则∠AED的度数为__________.
练习2-8 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点.若∠BOC=40°,则∠D的度数为 ( )
A.100° B.110° C.120° D.130°
练习2-9如图,PA、PB切⊙O于A. B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为___.
练习2-10(2020·陕西·中考模拟) 如图,点A、B、C、D在⊙O上,弧CB=弧CD,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
练习2-11如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与 AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
练习2-12如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止。设∠POF=x°,则x的取值范围是( )
A. 30?x?60 B. 30?x?90 C. 30?x?120 D. 60?x?120
练习2-13如图,四边形 ABCD 是菱形,⊙O 经过点 A、C、D,与 BC 相交于点 E,连接 AC、AE.若∠D=80°,则∠EAC 的度数为( )
A.20° B.35° C.40° D.55°
练习2-14如图,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是 ( )
A.15° B.30° C.45° D.60°
练习2-15如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为 .
练习2-16如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC= .
练习2-17如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为 .
练习2-18如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD= .
练习2-19如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
练习2-20如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
【经典例题3】如图,点A是量角器直径的一个端点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ.若点P对应135°(45°),则∠PQB的度数为( )
A.65° B.67.5° C.60° D.80°
【解析】连接OP,如图,则∠AOP=135°,
∴∠ABP=12∠AOP=67.5°.
∵PB=PQ,
∴∠PQB=∠ABP=67.5°.
故选:B.
练习3-1如图所示,量角器外缘边上有A、P、Q三点,它们所表示的读数分别是180°,,30°,则∠PAQ的大小为( )
A.10° B.20° C.30° D.40°
练习3-2如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C旋转,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是 .
练习3-3将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
练习3-4如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 .
题型四:与圆结合,利用圆的基本性质进行转化求解
【经典例题4】(攀枝花中考)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
练习4-1如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A. B. C.2 D.
练习4-2如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为_____.
练习4-3如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B. C. D.
练习4-4【转化思想】如图,求∠1的正切值.
练习4-5某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
A. B. C. D.
练习4-6(20年烟台一模)某数学研究性学习小组制作了如下的三角函数计算图尺来测量0°—90°的三角函数值:在一个圆心角为90°的扇形OAB中,以OB为直径在扇形内部画半圆M,将一根笔直的、长度等于OB的细木条分成10等份,并标上0到10刻度,将木条0刻度端点与点O重合,另一端点C落在圆弧AB上,木条OC与半圆M交点D.设∠AOC的度数是α,则通过读取点D处木条上的刻度可以( )
A.读取sinα的值,结果最小保留到百分位
B.读取sinα的值,结果最小保留到十分位
C.读取cosα的值,结果最小保留到百分位
D.读取cosα的值,结果最小保留到十分位
参考答案:
练习2-1如图,四边形ABCD内接于☉O,若四边形OABC是平行四边形,则∠ADC的大小为( )
A.45° B.50° C.60° D.75°
【解析】设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=β,∠AOC=α;而α+β=180°,
∴,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
练习2-2如图,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63 ?,那么∠B= ?.
【解析】连接DE、CE,则∠2=θ,∠5=∠6=2θ,
∵∠6是△BDE的外角,
∴∠6=∠2+∠ABC=2θ,
∵∠5+∠6+∠1=180°,
∴4θ+∠1=180°①,
在△ACE中,
∵AE=CE,
∴∠3=∠CAE=63°,
∴∠4=180°?∠3?∠CAE=180°?63°?63°=54°,
∵∠4+∠1+∠2=180°,即54°+∠1+θ=180°②,
①②联立得,θ=18°.
故答案为:18°.
练习2-3(毕节中考)如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
A.30° B.50° C.60° D.70°
【解析】∵∠ACD=30°,
∴∠ABD=30°,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD=90°-∠ABD=60°.
故选C.
练习2-4(泰安中考)如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
【解析】∵连接OC,
∵△ABC内接于⊙O,∠A=α,
∴∠BOC=2∠A=2α,
∵OB=OC,
∴∠OBC=∠OCB==90°.
故选D.
练习2-5如图,在⊙O 中,∠BAC=15°,∠ADC=20°,则∠ABO 的度数为( )
A.70° B.55° C.45° D.35°
【解析】连接OA、OC,
∵∠BAC=15°,∠ADC=20°,
∴∠AOB=2(∠ADC+∠BAC)=70°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°?∠AOB)=55°.
故选:B.
练习2-6如图,AB为半圆O的直径,延长AB到点P,使BP=AB,PC切半圆O于点C,点D是上和点C不重合的一点,则∠D的度数为__________.
【解析】
连接OC,
∵PC切半圆O于点C,
∴OC⊥PC,
∴OC=OB=PB,
∴∠P=30°,即∠COP=60°,
∴∠CDB=∠COP=30°.
练习2-7如图所示,已知点E是⊙O上的点,B、C分别是劣弧AD的三等分点,∠BOC=,则∠AED的度数为__________.
【解析】∵B、C分别是劣弧AD的三等分点,∠BOC=46°,
∴∠AOD=138°,
∴∠AED=138°÷2=69°.
练习2-8 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点.若∠BOC=40°,则∠D的度数为 ( )
A.100° B.110° C.120° D.130°
【解析】∴∠AOC=180°?40°=140°,
∴∠D=12×(360°?140°)=110°,
故选:B.
练习2-9如图,PA、PB切⊙O于A. B两点,连接OP交AB于点C,交弧AB于点D,∠APB=70°,点Q为优弧AmB上一点,OQ∥PB,则∠OQA的大小为___.
【解析】如图,连接OA.
∵PA,PB是⊙O的切线,
∴∠OPB=∠OPA=12∠APB=35°,PA⊥OA,
∴∠OAP=90°,
∴∠POA=90°?35°=55°,
∵OQ∥PB,
∴∠POQ=180°?∠OPB=145°,
∴∠AOQ=360°?145°?55°=160°,
∵OQ=OA,
∴∠OQA=∠OAQ=12(180°?∠AOQ)=10°,
故答案为10°.
练习2-10(2020·陕西·中考模拟) 如图,点A、B、C、D在⊙O上,弧CB=弧CD,∠CAD=30°,∠ACD=50°,则∠ADB=( )
A.30° B.50° C.70° D.80°
【解析】弧CB=弧CD,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ACB=∠ADB=180°?∠CAB?∠ABC=180°?50°?30°?30°=70°.
故选:C.
练习2-11如图,AB 是⊙O 的直径,EF,EB 是⊙O 的弦,且 EF=EB,EF 与 AB 交于点 C, 连接 OF,若∠AOF=40°,则∠F 的度数是( )
【解析】连接FB.
∵∠AOF=40°,
∴∠FOB=180°?40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∴∠EFO=∠EFB?∠OFB=35°,
故答案为:35°.
练习2-12如图,已知EF是圆O的直径,把∠A为60°的直角三角板ABC的一条直角边BC放在直线EF上,斜边AB与O交于点P,点B与点O重合,且AC大于OE,将三角板ABC沿OE方向平移,使得点B与点E重合为止。设∠POF=x°,则x的取值范围是( )
A. 30?x?60 B. 30?x?90 C. 30?x?120 D. 60?x?120
【解析】开始移动时,x=30°,
移动开始后,∠POF逐渐增大,
最后当B与E重合时,∠POF取得最大值,
则根据同弧所对的圆心角等于它所对圆周角的2倍得:
∠POF=2∠ABC=2×30°=60°,
故x的取值范围是30?x?60.
故选A.
练习2-13如图,四边形 ABCD 是菱形,⊙O 经过点 A、C、D,与 BC 相交于点 E,连接 AC、AE.若∠D=80°,则∠EAC 的度数为( )
A.20° B.35° C.40° D.55°
【解析】四边形ABCD是菱形,∠D=80°,
∴∠ACB=∠DCB=(180°?∠D)=50°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=80°,
∴∠EAC=∠AEB?∠ACE=30°,
故选:C.
练习2-14如图,☉A过点O(0,0),C(,0),D(0,1),点B是x轴下方☉A上的一点,连接BO,BD,则∠OBD的度数是 ( B )
A.15° B.30° C.45° D.60°
【解析】由题意得∠COD=90°,
∵D(0,1),C(,0),
∴OD=1,OC=,
∴CD=,
勾股定理
∴∠OCD=30°,
含30度角的直角三角形的判定
∴∠OBD=∠OCD=30°.
同弧或等弧所对的圆周角相等
故选B.
练习2-15如图,点A,B,C,D在⊙O上,∠ABO=40°,∠BCD=112°,E是AD中点,则∠DOE的度数为 .
【解析】连接OA,
∵OA=OB,∠ABO=40°,
∴∠OAB=∠ABO=40°,
∵∠BCD=112°,
∴∠BAD=180°﹣∠BCD=68°,
∴∠OAE=∠BAD﹣∠OAB=28°,
∵OA=OD,
∴∠ODA=∠OAD=28°
∵E是AD中点,
∴OE⊥AD,
∴∠DOE=90°﹣∠ODA=62°.
故答案为:62°.
练习2-16如图,△ABC内接于⊙O,弦DC⊥BC,已知⊙O的半径为5cm,弦BC长为6cm,则tan∠BAC= .
【解析】连接BD,
∵弦DC⊥BC,
∴∠BCD=90°,
∴BD是直径,
∵⊙O的半径为5cm,弦BC长为6cm,
∴BD=10cm,
∴CD==8cm,
∴tan∠BAC=tan∠BDC===.
故答案为:.
练习2-17如图,AC与BD交于P,AD、BC延长交于点E,∠AEC=37°,∠CAE=31°,则∠APB的度数为 .
【解析】∵∠ACB为△ACE的外角,
∴∠ACE=∠A+∠AEC
∵,∠AEC=37°,∠CAE=31°,
∴∠ACE=68°.
由圆周角定理,得∠ADB=∠ACB,
∴∠ADB=68°,
∴∠APB=∠A+∠ADB=31°+68°=99°,
故答案为99°.
练习2-18如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD= .
【解析】∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A=90°﹣∠ABD=90°﹣54°=36°,
∴∠BCD=∠A=36°,
故答案为36°.
练习2-19如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=56°,则α的度数是( )
A.52° B.60° C.72° D.76°
【解析】连接OC,OD,
∵∠BAO=∠CBO=∠DCO=∠EDO=α,
∵OA=OB=OC,
∴∠ABO=∠BCO=α,
∴∠AOB=∠BOC=∠COD=∠DOE=180°﹣2α,
∴4∠AOB+∠AOE=360°,
∴∠AOB=76°,
∴在等腰三角形AOB中,
∠α=∠BAO==52°.
故选:A.
练习2-20如图,圆心为C、直径为MN的半圆上有不同的两点A、B,在CN上有一点P,∠CBP=∠CAP=10°,若的度数是40°,则的度数是( )
A.10° B.15° C.20° D.25°
【解析】∵的度数是40°,
∴∠ACM=40°
∵∠CBP=∠CAP=10°,
∴A、C、P、B四点共圆,
∴∠ACM=∠ABP=40°,
∵∠CPB=10°,
∴∠ABC=40°﹣10°=30°,
∵AC=BC,
∴∠CAB=∠ABC=30°,
∴∠ACB=120°,
∴∠BCN=180°﹣∠ACM﹣∠ACB=20°,
∴的度数是20°.
故选:C.
【经典例题3】如图,点A是量角器直径的一个端点,点B在半圆周上,点P在上,点Q在AB上,且PB=PQ.若点P对应135°(45°),则∠PQB的度数为( )
A.65° B.67.5° C.60° D.80°
【解析】连接OP,如图,则∠AOP=135°,
∴∠ABP=12∠AOP=67.5°.
∵PB=PQ,
∴∠PQB=∠ABP=67.5°.
故选:B.
练习3-1如图所示,量角器外缘边上有A、P、Q三点,它们所表示的读数分别是180°,,30°,则∠PAQ的大小为( )
A.10° B.20° C.30° D.40°
【解析】设量角器的圆心角为O,连接PO,QO,
知∠POQ=70°-30°=40°,
而∠PAQ为所对的圆周角,
为∠POQ的一半,
所以∠PAQ=∠POQ=×40°=20°.
练习3-2如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C旋转,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是 .
【解析】①设CD′交AB于E,设AB的中点为O,连接OD′当EB=EC,此时∠EBC=∠ECB=40°,易知∠BOD′=2∠BCD′=80°,
∴点D′在量角器上对应的度数是80°;
②设CD″交AB于F,连接OD″,当BF=BC时,∠BCD″=70°,
易知∠BOD″=2∠BCD″=140°,
∴点D″在量角器上对应的度数是140°;
故答案为80°或140°
练习3-3将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为 .
【解析】设半圆圆心为O,连OA,OB,如图,
∵∠ACB=∠AOB,
而∠AOB=86°﹣30°=56°,
∴∠ACB=×56°=28°.
故答案为:28°.
练习3-4如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为 .
【解析】∵一块直角三角板ABC的斜边AB与量角器的直径重合,
∴点A、B、C、D都在以AB为直径的圆上,
∵点D对应54°,即∠AOD=54°,
∴∠ACD=∠AOD=27°,
∴∠BCD=90°﹣∠ACD=63°.
故答案为:63°.
题型四:与圆结合,利用圆的基本性质进行转化求解
【经典例题4】(攀枝花中考)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=( )
A. B. C. D.
练习4-1如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于( )
A. B. C.2 D.
练习4-2如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为_____.
练习4-3如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A. B. C. D.
练习4-4【转化思想】如图,求∠1的正切值.
练习4-5某数学研究性学习小组制作了如下的三角函数计算图尺:在半径为1的半圆形量角器中,画一个直径为1的圆,把刻度尺CA的0刻度固定在半圆的圆心O处,刻度尺可以绕点O旋转.从图中所示的图尺可读出sin∠AOB的值是( )
A. B. C. D.
练习4-6(20年烟台一模)某数学研究性学习小组制作了如下的三角函数计算图尺来测量0°—90°的三角函数值:在一个圆心角为90°的扇形OAB中,以OB为直径在扇形内部画半圆M,将一根笔直的、长度等于OB的细木条分成10等份,并标上0到10刻度,将木条0刻度端点与点O重合,另一端点C落在圆弧AB上,木条OC与半圆M交点D.设∠AOC的度数是α,则通过读取点D处木条上的刻度可以( )
A.读取sinα的值,结果最小保留到百分位
B.读取sinα的值,结果最小保留到十分位
C.读取cosα的值,结果最小保留到百分位
D.读取cosα的值,结果最小保留到十分位
练习4-7如图,点A、B、O是正方形网格上的三个格点,⊙O的半径是OA,点P是优弧上的一点,则tan∠APB的值是( ).
A.1 B. C. D.
练习4-8(20年济宁中考)如图,是正方形ABCD的内切圆,切点分别为E、F、G、H,ED与相交于点M,则sin∠MFG的值为 .
【经典例题4】D
练习4-1 、、C、、D、A、A
练习4-8 【提示】连接EG。
同课章节目录
