7.3离散型最基变量的均值与方差-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修三练习(Word版含答案)
文档属性
| 名称 | 7.3离散型最基变量的均值与方差-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修三练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 37.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 18:54:45 | ||
图片预览



文档简介
离散型最基变量的均值与方差练习
一、单选题
设随机变量的概率分布为
ξ
0
1
2
P
p3
p3
1?23p
则ξ的数学期望E(ξ)的最小值是(??? )
A. 12 B. 0
C. 2 D. 随p的变化而变化
设E(ξ)=10,E(η)=3,则E(3ξ+5η)为(????)
A. 15 B. 30 C. 40 D. 45
如果随机变量ξ的取值是a1,a2,a3,a4,a5,a6,ξ数学期望是3,那么2(a1?3),2(a2?3),2(a3?3),2(a4?3),2(a5?3),2(a6?3)的数学期望是(??? )
A. 0 B. 1 C. 2 D. 3
设随机变量X,Y满足:Y=3X?1,X~B(2,p),若P(X≥1)=59,则D(Y)=(????)
A. 4 B. 5 C. 6 D. 7
某人进行投篮训练100次,每次命中的概率为0.8(相互独立),则命中次数的标准差等于(????)
A. 20 B. 80 C. 16 D. 4
甲盒子装有3个红球,1个黄球,乙盒中装有1个红球,3个黄球,同时从甲乙两盒中取出i(i=1,2,3)个球交换,分别记甲乙两个盒子中红球个数的数学期望为E1(i),E2(i)则以下结论错误的是(????)
A. E1(1)>E2(1) B. E1(2)=E2(2)
C. E1(1)+E2(1)=4 D. E1(3)袋中有8只球,编号分别为1,2,3,4,5,6,7,8,现从中任取3只球,以ξ表示取出的3只球中最大号码与最小号码的差,则E(ξ)=(????)
A. 4 B. 4.5 C. 5 D. 5.5
设0X
0
a
1
P
13
13
13
则当a在(0,1)内增大时,(????)
A. V(X)增大 B. V(X)减小
C. V(X)先增大后减小 D. V(X)先减小后增大
同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)等于(????)
A. 158 B. 154 C. 52 D. 5
已知随机变量ξ+η=8,若ξ∽B(10,0.4),则E(η),D(η)分别是(??? )
A. 4和2.4 B. 2和2.4 C. 6和2.4 D. 4和5.6
已知离散型随机变量X的分布列如下:
X
1
3
5
P
0.5
m
0.2
则其均值E(X)等于(????)
A. 1 B. 0.6 C. 2+3m D. 2.4
二、单空题
在一次商业活动中,某人获利300元的概率为0.6,亏损100元的概率为0.4,此人在这样的一次商业活动中获利的均值是________.
随机抛掷一个骰子,所得点数X的均值为________.
将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X,则X的均值EX=??????????.
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为ξ;如果出现一奇一偶,则将它们的差的绝对值记为ξ,则随机变量ξ的数学期望为______.
已知在10件产品中可能存在次品,从中抽取2件检查,其次品数为ξ,已知P(ξ=1)=1645,且该产品的次品率不超过40%,则这10件产品的次品率为______________.
三、解答题(本大题共3小题,共36.0分)
有一批数值非常多的产品,其次品率是15%,对这批产品进行抽查,每次抽出1件.如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次,求抽查次数X的数学期望(结果保留三位有效数字).
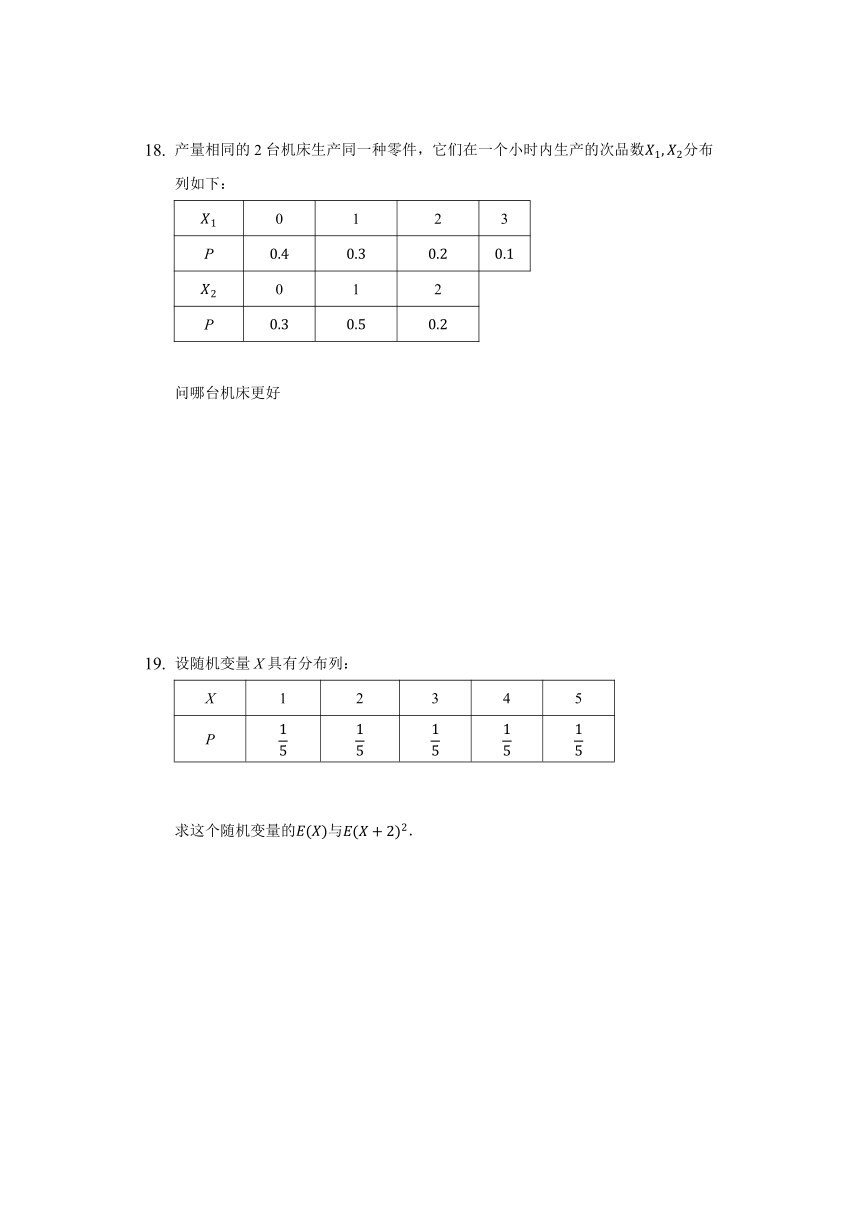
产量相同的2台机床生产同一种零件,它们在一个小时内生产的次品数X1,X2分布列如下:
X1
0
1
2
3
P
0.4
0.3
0.2
0.1
X2
0
1
2
P
0.3
0.5
0.2
问哪台机床更好
设随机变量X具有分布列:
X
1
2
3
4
5
P
15
15
15
15
15
求这个随机变量的E(X)与E(X+2)2.
答案和解析
1.【答案】A
2.【答案】D
3.【答案】A
4.【答案】A
【解析】:∵随机变量X,Y满足:Y=3X?1,X~B(2,p),P(X≥1)=59,
∴P(X=0)=1?P(X≥1)=C20(1?p)2=49,
解得p=13,∴X~B(2,13),
∴D(X)=2×13×(1?13)=49,
∴D(Y)=9E(X)=9×49=4.
5.【答案】D
【解答】
解:由题意,某人进行投篮训练100次,每次命中的概率为0.8(相互独立),则不命中的概率为0.2,
从而命中次数的标准差为100×0.8×0.2=4,
6.【答案】D
【解答】
解:用X表示交换后甲盒子中的红球数,Y表示交换后乙盒子中的红球数,
当i=1时,
则P(X=2)=P(Y=2)=C31?C31C41?C41=916,P(X=4)=P(Y=0)=C11?C11C41?C41=116,P(X=3)=P(Y=1)=C31?C11C41?C41×2=38,
∴E1(1)=2×916+3×38+4×116=52,E2(1)=2×916+0×116+1×38=32.
故A正确,C正确,
当i=2时,
P(X=1)=P(Y=3)=C32?C32C42?C42=14,P(X=2)=P(Y=2)=C31·C11C42?C32C42×2=12,P(X=3)=P(Y=1)=C31·C11C42?C31·C11C42=14.
∴E1(2)=1×14+2×12+3×14=2,E2(2)=3×14+2×12+1×14=2.
故B正确.
当n=3时,
P(X=0)=P(Y=4)=C33?C33C43?C43=116,P(X=1)=P(Y=3)=C33C43?C32·C11C43×2=38,P(X=2)=P(Y=2)=916,
∴E1(3)=0×116+1×38+2×916=32.
7.【答案】B
【解】解:由题意知ξ的可能取值为2,3,4,5,6,7,
P(ξ=2)=C61C83=656,
P(ξ=3)=C51(C22C21)C83=1056,
P(ξ=4)=C41(C22C31)C83=1256,
P(ξ=5)=C31(C22C41)C83=1256,
P(ξ=6)=C21(C22C51)C83=1056,
P(ξ=7)=C22C61C83=656,
∴E(ξ)=2×656+3×1056+4×1256+5×1256+6×1056+7×656=4.5.
8.【答案】D
【解答】
解:由题意可得,E(X)=13(a+1),
所以V(X)=(a+1)227+(1?2a)227+(a?2)227
=6a2?6a+627=29[(a?12)2+34],
所以当a在(0,1)内增大时,V(X)先减小后增大,
9.【答案】A
【解答】
解:两枚硬币同时出现反面的概率为12×12=14,
故ξ~B(10,14),
因此D(ξ)=10×14×(1?14)=158.
故选A.
10.【答案】A
【解答】
解:因为ξ?B(10,0.4),
所以E(ξ)=10×0.4=4,
D(ξ)=10×0.4×(1?0.4)=2.4,
又ξ+η=8,
所以η=8?ξ,
所以E(η)=8?E(ξ)=8?4=4,
D(η)=(?1)2D(ξ)=2.4,
故选A.
11.【答案】D
【解答】
解:∵分布列中出现的所有的概率之和等于1,
∴0.5+m+0.2=1,解得m=0.3,
∴E(X)=1×0.5+3×0.3+5×0.2=2.4.
故选D.
12.【答案】140
13.【答案】3.5
14.【答案】65
【解答】
解:∵125个小正方体中8个三面涂漆,36个两面涂漆,54个一面涂漆,27个没有涂漆,∴从中随机取一个正方体,涂漆面数X的均值EX=27125×0+54125×1+36125×2+8125×3=150125=65.
15.【答案】83
【解析】解:从分别标有1、2、3、4的四张卡片中任意抽取两张,共有C42=6种情况:1,2;1,3;1,4;2,3;2,4;3,4.
其中①出现两个偶数或两个奇数有1,3;2,4.两种情况,两个数的和分别为4,6.
②出现一奇一偶,有1,2;1,4;2,3;3,4.四种情况,则它们的差的绝对值分别为,1,3,1,1.
∴P(ξ=1)=12,P(ξ=3)=P(ξ=4)=P(ξ=6)=16.
∴Eξ=1×12+(3+4+6)×16=83.
16.【答案】20%
【解答】
?解:设10件产品中存在n件次品,从中抽取2件,其次品数为ξ,
由P(ξ=1)=1645?得Cn1·C10?n1C102=1645,
化简得n2?10n+16=0,
解得n=2或n=8;
又该产品的次品率不超过40%,
∴n≤4;
应取n=2,
∴这10件产品的次品率为?20%.
故答案为20%.
17.【答案】解:记“第i次取出正品”为事件Ai(i=1,2,…,9),“第i次取出次品”为事件Bi,则前i?1次取出正品,而第i次(i=1,2,…,9)取出次品的概率是P(X=i)=P(A1A2?Ai?1Bi)=P(A1)P(A2)?P(Ai?1)P(Bi)
=0.85×0.85×?×0.85×0.15=0.85i?1×0.15.
所以X的分布列为
X
1
2
3
4
5
6
7
8
9
10
P
0.15
0.1275
0.1084
0.092
0.0783
0.0666
0.0566
0.0481
0.0409
0.2316
EX=1×0.15+2×0.1275+?+10×0.231≈5.35.
18.【答案】解:因为E(X1)=0×0.4+1×0.3+2×0.2+3×0.1=1,
E(X2)=0×0.3+1×0.5+2×0.2=0.9.
所以第2台机床更好.
19.【答案】解:E(X)=1×15+2×15+3×15+4×15+5×15=3,
因为E(X)=1×15+2×15+3×15+4×15+5×15=3,
E(X2)=12×15+22×15+32×15+42×15+52×15=11,
所以E(X+2)2=E(X2+4X+4)=E(X2)+4E(X)+4=11+12+4=22.
一、单选题
设随机变量的概率分布为
ξ
0
1
2
P
p3
p3
1?23p
则ξ的数学期望E(ξ)的最小值是(??? )
A. 12 B. 0
C. 2 D. 随p的变化而变化
设E(ξ)=10,E(η)=3,则E(3ξ+5η)为(????)
A. 15 B. 30 C. 40 D. 45
如果随机变量ξ的取值是a1,a2,a3,a4,a5,a6,ξ数学期望是3,那么2(a1?3),2(a2?3),2(a3?3),2(a4?3),2(a5?3),2(a6?3)的数学期望是(??? )
A. 0 B. 1 C. 2 D. 3
设随机变量X,Y满足:Y=3X?1,X~B(2,p),若P(X≥1)=59,则D(Y)=(????)
A. 4 B. 5 C. 6 D. 7
某人进行投篮训练100次,每次命中的概率为0.8(相互独立),则命中次数的标准差等于(????)
A. 20 B. 80 C. 16 D. 4
甲盒子装有3个红球,1个黄球,乙盒中装有1个红球,3个黄球,同时从甲乙两盒中取出i(i=1,2,3)个球交换,分别记甲乙两个盒子中红球个数的数学期望为E1(i),E2(i)则以下结论错误的是(????)
A. E1(1)>E2(1) B. E1(2)=E2(2)
C. E1(1)+E2(1)=4 D. E1(3)
A. 4 B. 4.5 C. 5 D. 5.5
设0
0
a
1
P
13
13
13
则当a在(0,1)内增大时,(????)
A. V(X)增大 B. V(X)减小
C. V(X)先增大后减小 D. V(X)先减小后增大
同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)等于(????)
A. 158 B. 154 C. 52 D. 5
已知随机变量ξ+η=8,若ξ∽B(10,0.4),则E(η),D(η)分别是(??? )
A. 4和2.4 B. 2和2.4 C. 6和2.4 D. 4和5.6
已知离散型随机变量X的分布列如下:
X
1
3
5
P
0.5
m
0.2
则其均值E(X)等于(????)
A. 1 B. 0.6 C. 2+3m D. 2.4
二、单空题
在一次商业活动中,某人获利300元的概率为0.6,亏损100元的概率为0.4,此人在这样的一次商业活动中获利的均值是________.
随机抛掷一个骰子,所得点数X的均值为________.
将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的油漆面数为X,则X的均值EX=??????????.
某人从标有1、2、3、4的四张卡片中任意抽取两张.约定如下:如果出现两个偶数或两个奇数,就将两数相加的和记为ξ;如果出现一奇一偶,则将它们的差的绝对值记为ξ,则随机变量ξ的数学期望为______.
已知在10件产品中可能存在次品,从中抽取2件检查,其次品数为ξ,已知P(ξ=1)=1645,且该产品的次品率不超过40%,则这10件产品的次品率为______________.
三、解答题(本大题共3小题,共36.0分)
有一批数值非常多的产品,其次品率是15%,对这批产品进行抽查,每次抽出1件.如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品,但抽查次数最多不超过10次,求抽查次数X的数学期望(结果保留三位有效数字).
产量相同的2台机床生产同一种零件,它们在一个小时内生产的次品数X1,X2分布列如下:
X1
0
1
2
3
P
0.4
0.3
0.2
0.1
X2
0
1
2
P
0.3
0.5
0.2
问哪台机床更好
设随机变量X具有分布列:
X
1
2
3
4
5
P
15
15
15
15
15
求这个随机变量的E(X)与E(X+2)2.
答案和解析
1.【答案】A
2.【答案】D
3.【答案】A
4.【答案】A
【解析】:∵随机变量X,Y满足:Y=3X?1,X~B(2,p),P(X≥1)=59,
∴P(X=0)=1?P(X≥1)=C20(1?p)2=49,
解得p=13,∴X~B(2,13),
∴D(X)=2×13×(1?13)=49,
∴D(Y)=9E(X)=9×49=4.
5.【答案】D
【解答】
解:由题意,某人进行投篮训练100次,每次命中的概率为0.8(相互独立),则不命中的概率为0.2,
从而命中次数的标准差为100×0.8×0.2=4,
6.【答案】D
【解答】
解:用X表示交换后甲盒子中的红球数,Y表示交换后乙盒子中的红球数,
当i=1时,
则P(X=2)=P(Y=2)=C31?C31C41?C41=916,P(X=4)=P(Y=0)=C11?C11C41?C41=116,P(X=3)=P(Y=1)=C31?C11C41?C41×2=38,
∴E1(1)=2×916+3×38+4×116=52,E2(1)=2×916+0×116+1×38=32.
故A正确,C正确,
当i=2时,
P(X=1)=P(Y=3)=C32?C32C42?C42=14,P(X=2)=P(Y=2)=C31·C11C42?C32C42×2=12,P(X=3)=P(Y=1)=C31·C11C42?C31·C11C42=14.
∴E1(2)=1×14+2×12+3×14=2,E2(2)=3×14+2×12+1×14=2.
故B正确.
当n=3时,
P(X=0)=P(Y=4)=C33?C33C43?C43=116,P(X=1)=P(Y=3)=C33C43?C32·C11C43×2=38,P(X=2)=P(Y=2)=916,
∴E1(3)=0×116+1×38+2×916=32.
7.【答案】B
【解】解:由题意知ξ的可能取值为2,3,4,5,6,7,
P(ξ=2)=C61C83=656,
P(ξ=3)=C51(C22C21)C83=1056,
P(ξ=4)=C41(C22C31)C83=1256,
P(ξ=5)=C31(C22C41)C83=1256,
P(ξ=6)=C21(C22C51)C83=1056,
P(ξ=7)=C22C61C83=656,
∴E(ξ)=2×656+3×1056+4×1256+5×1256+6×1056+7×656=4.5.
8.【答案】D
【解答】
解:由题意可得,E(X)=13(a+1),
所以V(X)=(a+1)227+(1?2a)227+(a?2)227
=6a2?6a+627=29[(a?12)2+34],
所以当a在(0,1)内增大时,V(X)先减小后增大,
9.【答案】A
【解答】
解:两枚硬币同时出现反面的概率为12×12=14,
故ξ~B(10,14),
因此D(ξ)=10×14×(1?14)=158.
故选A.
10.【答案】A
【解答】
解:因为ξ?B(10,0.4),
所以E(ξ)=10×0.4=4,
D(ξ)=10×0.4×(1?0.4)=2.4,
又ξ+η=8,
所以η=8?ξ,
所以E(η)=8?E(ξ)=8?4=4,
D(η)=(?1)2D(ξ)=2.4,
故选A.
11.【答案】D
【解答】
解:∵分布列中出现的所有的概率之和等于1,
∴0.5+m+0.2=1,解得m=0.3,
∴E(X)=1×0.5+3×0.3+5×0.2=2.4.
故选D.
12.【答案】140
13.【答案】3.5
14.【答案】65
【解答】
解:∵125个小正方体中8个三面涂漆,36个两面涂漆,54个一面涂漆,27个没有涂漆,∴从中随机取一个正方体,涂漆面数X的均值EX=27125×0+54125×1+36125×2+8125×3=150125=65.
15.【答案】83
【解析】解:从分别标有1、2、3、4的四张卡片中任意抽取两张,共有C42=6种情况:1,2;1,3;1,4;2,3;2,4;3,4.
其中①出现两个偶数或两个奇数有1,3;2,4.两种情况,两个数的和分别为4,6.
②出现一奇一偶,有1,2;1,4;2,3;3,4.四种情况,则它们的差的绝对值分别为,1,3,1,1.
∴P(ξ=1)=12,P(ξ=3)=P(ξ=4)=P(ξ=6)=16.
∴Eξ=1×12+(3+4+6)×16=83.
16.【答案】20%
【解答】
?解:设10件产品中存在n件次品,从中抽取2件,其次品数为ξ,
由P(ξ=1)=1645?得Cn1·C10?n1C102=1645,
化简得n2?10n+16=0,
解得n=2或n=8;
又该产品的次品率不超过40%,
∴n≤4;
应取n=2,
∴这10件产品的次品率为?20%.
故答案为20%.
17.【答案】解:记“第i次取出正品”为事件Ai(i=1,2,…,9),“第i次取出次品”为事件Bi,则前i?1次取出正品,而第i次(i=1,2,…,9)取出次品的概率是P(X=i)=P(A1A2?Ai?1Bi)=P(A1)P(A2)?P(Ai?1)P(Bi)
=0.85×0.85×?×0.85×0.15=0.85i?1×0.15.
所以X的分布列为
X
1
2
3
4
5
6
7
8
9
10
P
0.15
0.1275
0.1084
0.092
0.0783
0.0666
0.0566
0.0481
0.0409
0.2316
EX=1×0.15+2×0.1275+?+10×0.231≈5.35.
18.【答案】解:因为E(X1)=0×0.4+1×0.3+2×0.2+3×0.1=1,
E(X2)=0×0.3+1×0.5+2×0.2=0.9.
所以第2台机床更好.
19.【答案】解:E(X)=1×15+2×15+3×15+4×15+5×15=3,
因为E(X)=1×15+2×15+3×15+4×15+5×15=3,
E(X2)=12×15+22×15+32×15+42×15+52×15=11,
所以E(X+2)2=E(X2+4X+4)=E(X2)+4E(X)+4=11+12+4=22.
