2020-2021学年北师大版七年级数学下册5.3 简单的轴对称图形(六) 同步练习题(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册5.3 简单的轴对称图形(六) 同步练习题(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 23:05:47 | ||
图片预览


文档简介
2020-2021学年北师大版七年级数学下册第五章
5.3.6简单的轴对称图形(六)
同步练习题
A组(基础题)
一、填空题
1.如图,已知∠AOB=30°,P是∠AOB平分线上的一点,PC∥OA,PD⊥OA.若PC=4,则PD=_____.
2.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D.若CD=3,则BD=_____.
3.在△ABC中,AB=5,AC=8,AD是△ABC的平分线,则△ABD与△ACD的面积之比是5∶8.
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于_____.
二、选择题
5.下列说法不正确的是(
)
A.角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
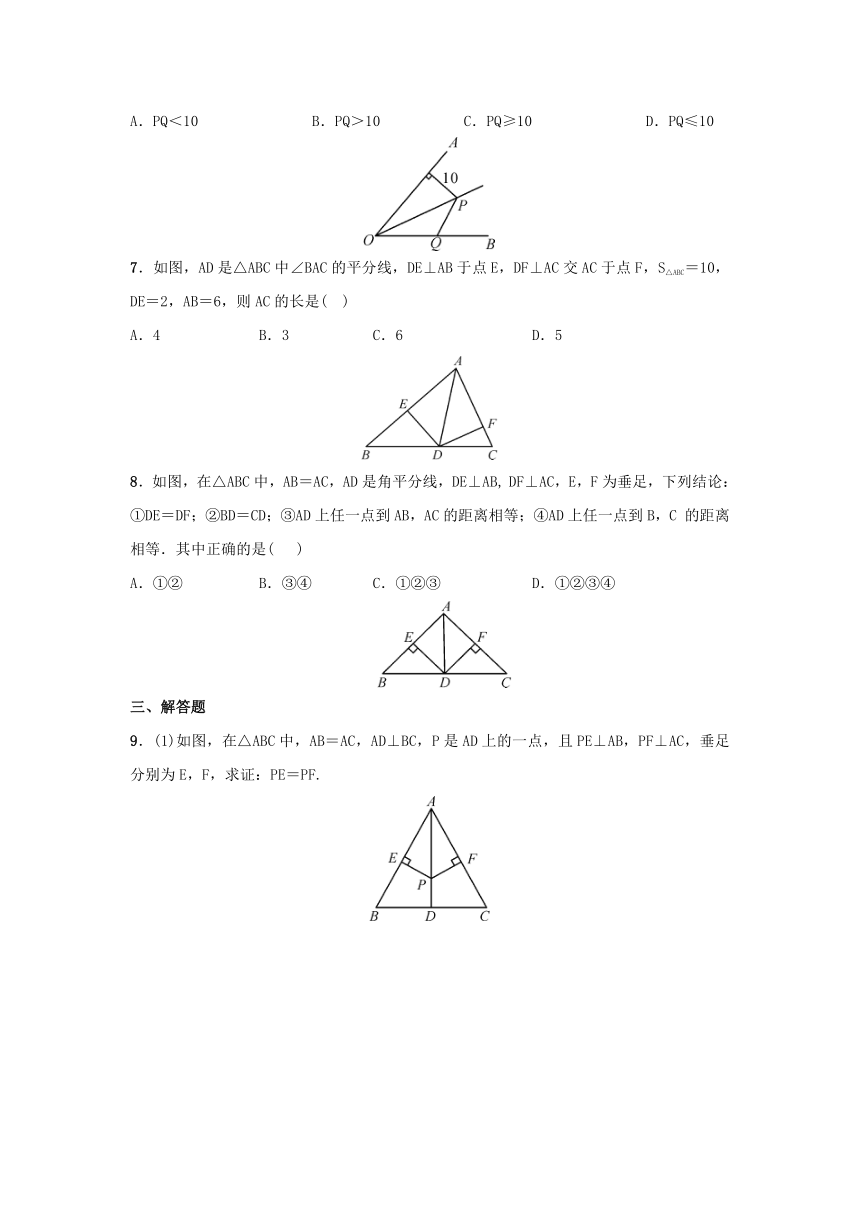
6.如图,点P在∠AOB的平分线上,点P到OA边的距离等于10,点Q是OB边上的任意一点,下列选项正确的是(
)
A.PQ<10
B.PQ>10
C.PQ≥10
D.PQ≤10
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=10,DE=2,AB=6,则AC的长是(
)
A.4
B.3
C.6
D.5
8.如图,在△ABC中,AB=AC,AD是角平分线,DE⊥AB,
DF⊥AC,E,F为垂足,下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到B,C
的距离相等.其中正确的是(
)
A.①②
B.③④
C.①②③
D.①②③④
三、解答题
9.(1)如图,在△ABC中,AB=AC,AD⊥BC,P是AD上的一点,且PE⊥AB,PF⊥AC,垂足分别为E,F,求证:PE=PF.
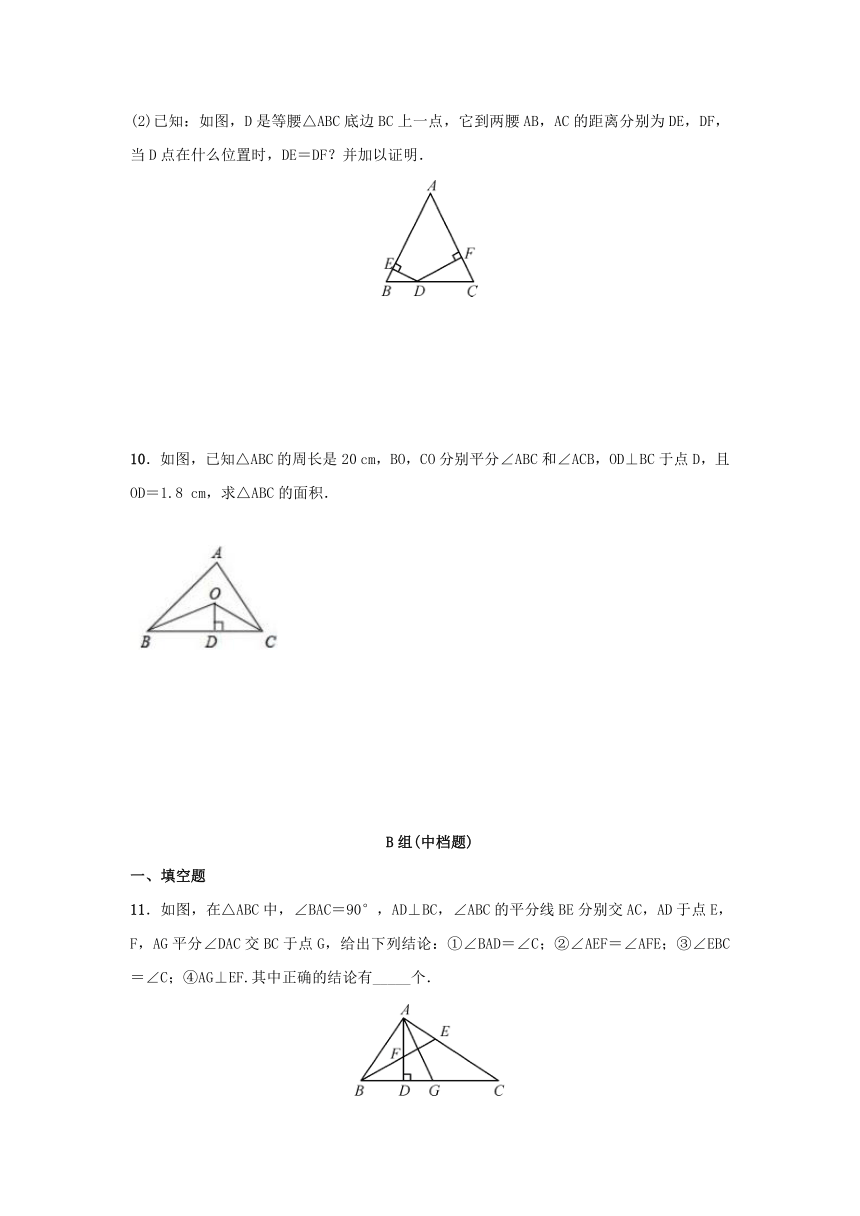
(2)已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF,当D点在什么位置时,DE=DF?并加以证明.
10.如图,已知△ABC的周长是20
cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=1.8
cm,求△ABC的面积.
B组(中档题)
一、填空题
11.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE分别交AC,AD于点E,F,AG平分∠DAC交BC于点G,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论有_____个.
12.如图,△ABC的三条角平分线交于点O,已知△ABC的周长为24,OD⊥AB,OD=3,则△ABC的面积为_____.
13.如图,在△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F,E分别为AC,AD上两动点,连接CE,EF.则CE+EF的最小值为_____.
二、解答题
14.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
C组(综合题)
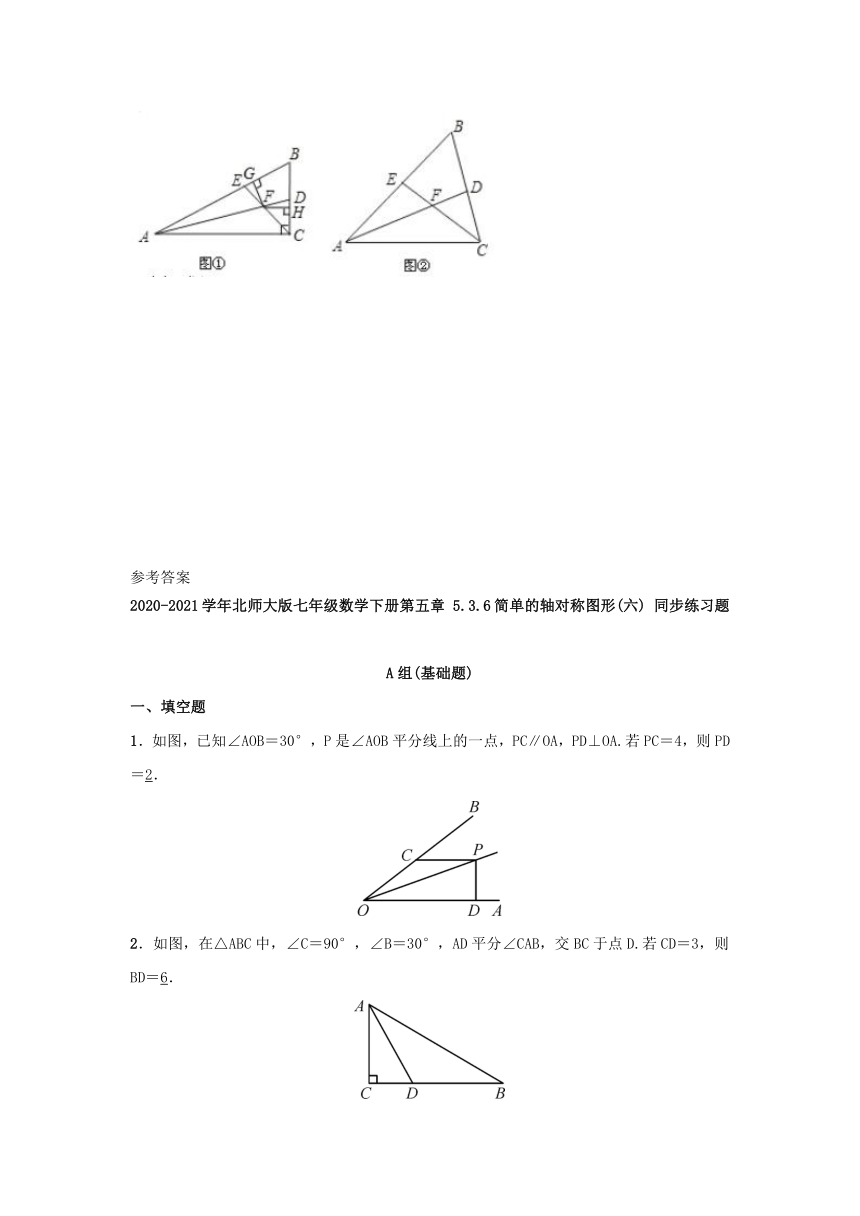
15.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,且FG⊥AB于点G,FH⊥BC于点H.
(1)试说明∠BEC=∠ADC的理由;
(2)请你判断FE与FD之间的数量关系,并说明理由;
(3)如图2,在△ABC中,如果∠ACB不是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?请说明理由.
参考答案
2020-2021学年北师大版七年级数学下册第五章
5.3.6简单的轴对称图形(六)
同步练习题
A组(基础题)
一、填空题
1.如图,已知∠AOB=30°,P是∠AOB平分线上的一点,PC∥OA,PD⊥OA.若PC=4,则PD=2.
2.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D.若CD=3,则BD=6.
3.在△ABC中,AB=5,AC=8,AD是△ABC的平分线,则△ABD与△ACD的面积之比是5∶8.
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于12.
二、选择题
5.下列说法不正确的是(D)
A.角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
6.如图,点P在∠AOB的平分线上,点P到OA边的距离等于10,点Q是OB边上的任意一点,下列选项正确的是(C)
A.PQ<10
B.PQ>10
C.PQ≥10
D.PQ≤10
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=10,DE=2,AB=6,则AC的长是(A)
A.4
B.3
C.6
D.5
8.如图,在△ABC中,AB=AC,AD是角平分线,DE⊥AB,
DF⊥AC,E,F为垂足,下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到B,C
的距离相等.其中正确的是(D)
A.①②
B.③④
C.①②③
D.①②③④
三、解答题
9.(1)如图,在△ABC中,AB=AC,AD⊥BC,P是AD上的一点,且PE⊥AB,PF⊥AC,垂足分别为E,F,求证:PE=PF.
证明:在△ABC中,
∵AB=AC,AD⊥BC,
∴AD是∠BAC的平分线.
又∵PE⊥AB,PF⊥AC,
∴PE=PF.
(2)已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF,当D点在什么位置时,DE=DF?并加以证明.
解:当D为BC的中点时,DE=DF.
证明:∵AD为等腰三角形底边上的中线,
∴AD平分∠BAC.
又∵DE⊥AB,DF⊥AC,
∴DE=DF.
10.如图,已知△ABC的周长是20
cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=1.8
cm,求△ABC的面积.
解:连接OA,过点O作OE⊥AB,OF⊥AC,垂足分别为E,F.
∵BO是∠ABC的平分线,且OD⊥BC,OE⊥AB,
∴OE=OD=1.8
cm.
同理,OF=OD=1.8
cm,
∴S△ABC=S△BOC+S△ABO+S△ACO=BC·OD+AB·OE+AC·OF=(BC+AB+AC)·OD=×20×1.8=18(cm2).
B组(中档题)
一、填空题
11.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE分别交AC,AD于点E,F,AG平分∠DAC交BC于点G,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论有3个.
12.如图,△ABC的三条角平分线交于点O,已知△ABC的周长为24,OD⊥AB,OD=3,则△ABC的面积为36.
13.如图,在△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F,E分别为AC,AD上两动点,连接CE,EF.则CE+EF的最小值为6.
二、解答题
14.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
证明:过点P作PE⊥OA于点E,PF⊥OB于点F,
∴∠PEC=∠PFD=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°.
∵∠PDO+∠PDF=180°,
∴∠PCE=∠PDF.
在△PCE和△PDF中,
∴△PCE≌△PDF(AAS).
∴PC=PD.
C组(综合题)
15.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,且FG⊥AB于点G,FH⊥BC于点H.
(1)试说明∠BEC=∠ADC的理由;
(2)请你判断FE与FD之间的数量关系,并说明理由;
(3)如图2,在△ABC中,如果∠ACB不是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?请说明理由.
图1
图2
解:(1)∵AD,CE分别是∠BAC,∠BCA的平分线,
∴∠DAC=∠DAB=∠BAC=15°,∠ACE=∠ACB=45°.
∴∠CDA=∠BAD+∠ABD=75°,∠BEC=∠BAC+∠ECA=75°.
∴∠BEC=∠ADC.
(2)相等,理由:
过点F作FH⊥BC于点H,作FG⊥AB于点G,连接BF,
∵点F是△ABC角平分线交点,
∴BF平分∠ABC.
∴HF=FG,∠DHF=∠EGF=90°.
由(1)得∠BEC=ADC,即∠GEF=∠HDF.
在△DHF和△EGF中,
∴△DHF≌△EGF(AAS).
∴FE=FD.
(3)成立.理由:过点F作FM⊥BC于点M,作FN⊥AB于点N,连接BF,
∵点F是△ABC角平分线交点,
∴BF平分∠ABC.∴MF=FN,∠DMF=∠ENF=90°.
∵∠ABC=60°,
∴∠MFN=360°-90°-90°-60°=120°.
∵∠CFA=180°-(∠FAC+∠FCA)=180°-(∠BAC+∠ACB)=180°-(180°-∠ABC)=180°-(180°-60°)=120°,
∴∠DFE=∠CFA=∠MFN=120°.
又∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠NFE.
在△DMF和△ENF中,
∴△DMF≌△ENF(ASA).
∴FE=FD.
5.3.6简单的轴对称图形(六)
同步练习题
A组(基础题)
一、填空题
1.如图,已知∠AOB=30°,P是∠AOB平分线上的一点,PC∥OA,PD⊥OA.若PC=4,则PD=_____.
2.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D.若CD=3,则BD=_____.
3.在△ABC中,AB=5,AC=8,AD是△ABC的平分线,则△ABD与△ACD的面积之比是5∶8.
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于_____.
二、选择题
5.下列说法不正确的是(
)
A.角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
6.如图,点P在∠AOB的平分线上,点P到OA边的距离等于10,点Q是OB边上的任意一点,下列选项正确的是(
)
A.PQ<10
B.PQ>10
C.PQ≥10
D.PQ≤10
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=10,DE=2,AB=6,则AC的长是(
)
A.4
B.3
C.6
D.5
8.如图,在△ABC中,AB=AC,AD是角平分线,DE⊥AB,
DF⊥AC,E,F为垂足,下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到B,C
的距离相等.其中正确的是(
)
A.①②
B.③④
C.①②③
D.①②③④
三、解答题
9.(1)如图,在△ABC中,AB=AC,AD⊥BC,P是AD上的一点,且PE⊥AB,PF⊥AC,垂足分别为E,F,求证:PE=PF.
(2)已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF,当D点在什么位置时,DE=DF?并加以证明.
10.如图,已知△ABC的周长是20
cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=1.8
cm,求△ABC的面积.
B组(中档题)
一、填空题
11.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE分别交AC,AD于点E,F,AG平分∠DAC交BC于点G,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论有_____个.
12.如图,△ABC的三条角平分线交于点O,已知△ABC的周长为24,OD⊥AB,OD=3,则△ABC的面积为_____.
13.如图,在△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F,E分别为AC,AD上两动点,连接CE,EF.则CE+EF的最小值为_____.
二、解答题
14.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
C组(综合题)
15.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,且FG⊥AB于点G,FH⊥BC于点H.
(1)试说明∠BEC=∠ADC的理由;
(2)请你判断FE与FD之间的数量关系,并说明理由;
(3)如图2,在△ABC中,如果∠ACB不是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?请说明理由.
参考答案
2020-2021学年北师大版七年级数学下册第五章
5.3.6简单的轴对称图形(六)
同步练习题
A组(基础题)
一、填空题
1.如图,已知∠AOB=30°,P是∠AOB平分线上的一点,PC∥OA,PD⊥OA.若PC=4,则PD=2.
2.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D.若CD=3,则BD=6.
3.在△ABC中,AB=5,AC=8,AD是△ABC的平分线,则△ABD与△ACD的面积之比是5∶8.
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于12.
二、选择题
5.下列说法不正确的是(D)
A.角平分线上的点到这个角两条边的距离相等
B.线段的垂直平分线上的点到这条线段的两个端点的距离相等
C.圆有无数条对称轴
D.等腰三角形的对称轴是底角的平分线所在的直线
6.如图,点P在∠AOB的平分线上,点P到OA边的距离等于10,点Q是OB边上的任意一点,下列选项正确的是(C)
A.PQ<10
B.PQ>10
C.PQ≥10
D.PQ≤10
7.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,DF⊥AC交AC于点F,S△ABC=10,DE=2,AB=6,则AC的长是(A)
A.4
B.3
C.6
D.5
8.如图,在△ABC中,AB=AC,AD是角平分线,DE⊥AB,
DF⊥AC,E,F为垂足,下列结论:①DE=DF;②BD=CD;③AD上任一点到AB,AC的距离相等;④AD上任一点到B,C
的距离相等.其中正确的是(D)
A.①②
B.③④
C.①②③
D.①②③④
三、解答题
9.(1)如图,在△ABC中,AB=AC,AD⊥BC,P是AD上的一点,且PE⊥AB,PF⊥AC,垂足分别为E,F,求证:PE=PF.
证明:在△ABC中,
∵AB=AC,AD⊥BC,
∴AD是∠BAC的平分线.
又∵PE⊥AB,PF⊥AC,
∴PE=PF.
(2)已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB,AC的距离分别为DE,DF,当D点在什么位置时,DE=DF?并加以证明.
解:当D为BC的中点时,DE=DF.
证明:∵AD为等腰三角形底边上的中线,
∴AD平分∠BAC.
又∵DE⊥AB,DF⊥AC,
∴DE=DF.
10.如图,已知△ABC的周长是20
cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=1.8
cm,求△ABC的面积.
解:连接OA,过点O作OE⊥AB,OF⊥AC,垂足分别为E,F.
∵BO是∠ABC的平分线,且OD⊥BC,OE⊥AB,
∴OE=OD=1.8
cm.
同理,OF=OD=1.8
cm,
∴S△ABC=S△BOC+S△ABO+S△ACO=BC·OD+AB·OE+AC·OF=(BC+AB+AC)·OD=×20×1.8=18(cm2).
B组(中档题)
一、填空题
11.如图,在△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE分别交AC,AD于点E,F,AG平分∠DAC交BC于点G,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF.其中正确的结论有3个.
12.如图,△ABC的三条角平分线交于点O,已知△ABC的周长为24,OD⊥AB,OD=3,则△ABC的面积为36.
13.如图,在△ABC中,AC=8,AB=10,△ABC的面积为30,AD平分∠BAC,F,E分别为AC,AD上两动点,连接CE,EF.则CE+EF的最小值为6.
二、解答题
14.如图,已知∠AOB=90°,OM是∠AOB的平分线,将三角尺的直角顶点P在射线OM上滑动,两直角边分别与OA,OB交于点C,D,求证:PC=PD.
证明:过点P作PE⊥OA于点E,PF⊥OB于点F,
∴∠PEC=∠PFD=90°.
∵OM是∠AOB的平分线,
∴PE=PF.
∵∠AOB=90°,∠CPD=90°,
∴∠PCE+∠PDO=360°-90°-90°=180°.
∵∠PDO+∠PDF=180°,
∴∠PCE=∠PDF.
在△PCE和△PDF中,
∴△PCE≌△PDF(AAS).
∴PC=PD.
C组(综合题)
15.如图1,在△ABC中,∠ACB是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F,且FG⊥AB于点G,FH⊥BC于点H.
(1)试说明∠BEC=∠ADC的理由;
(2)请你判断FE与FD之间的数量关系,并说明理由;
(3)如图2,在△ABC中,如果∠ACB不是直角,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,AD,CE相交于点F.请问,你在(2)中所得结论是否仍然成立?请说明理由.
图1
图2
解:(1)∵AD,CE分别是∠BAC,∠BCA的平分线,
∴∠DAC=∠DAB=∠BAC=15°,∠ACE=∠ACB=45°.
∴∠CDA=∠BAD+∠ABD=75°,∠BEC=∠BAC+∠ECA=75°.
∴∠BEC=∠ADC.
(2)相等,理由:
过点F作FH⊥BC于点H,作FG⊥AB于点G,连接BF,
∵点F是△ABC角平分线交点,
∴BF平分∠ABC.
∴HF=FG,∠DHF=∠EGF=90°.
由(1)得∠BEC=ADC,即∠GEF=∠HDF.
在△DHF和△EGF中,
∴△DHF≌△EGF(AAS).
∴FE=FD.
(3)成立.理由:过点F作FM⊥BC于点M,作FN⊥AB于点N,连接BF,
∵点F是△ABC角平分线交点,
∴BF平分∠ABC.∴MF=FN,∠DMF=∠ENF=90°.
∵∠ABC=60°,
∴∠MFN=360°-90°-90°-60°=120°.
∵∠CFA=180°-(∠FAC+∠FCA)=180°-(∠BAC+∠ACB)=180°-(180°-∠ABC)=180°-(180°-60°)=120°,
∴∠DFE=∠CFA=∠MFN=120°.
又∵∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,
∴∠DFM=∠NFE.
在△DMF和△ENF中,
∴△DMF≌△ENF(ASA).
∴FE=FD.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
