2020-2021学年七年级数学沪科版下册8.4 第2课时 公式法(共23张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学沪科版下册8.4 第2课时 公式法(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 18:08:32 | ||
图片预览



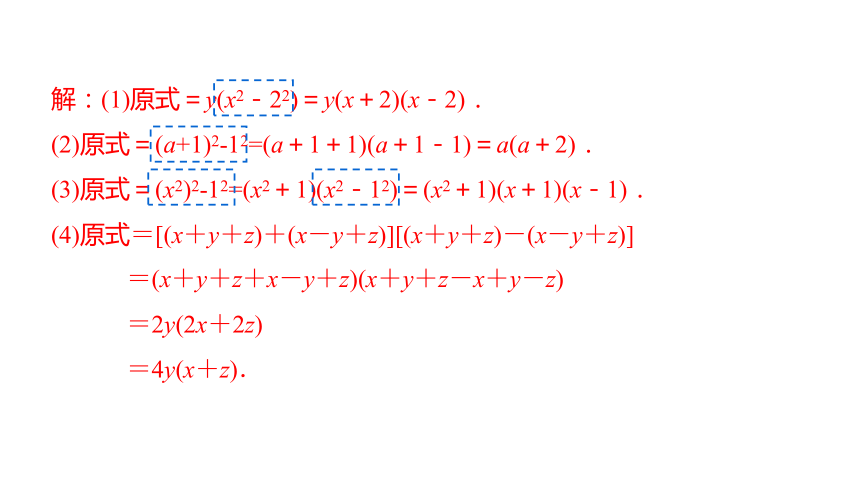


文档简介
(共23张PPT)
第8章
整式乘法与因式分解
8.4
第2课时
公式法
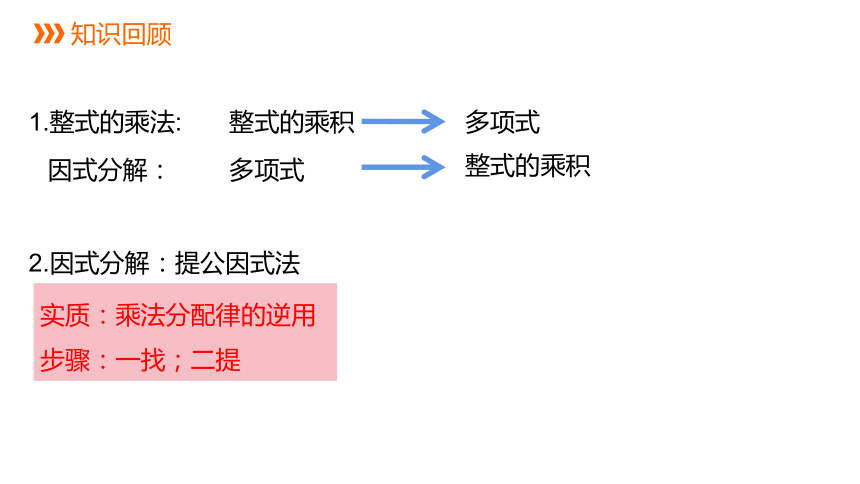
知识回顾
1.整式的乘法:
整式的乘积
因式分解:
多项式
多项式
整式的乘积
2.因式分解:提公因式法
实质:乘法分配律的逆用
步骤:一找;二提
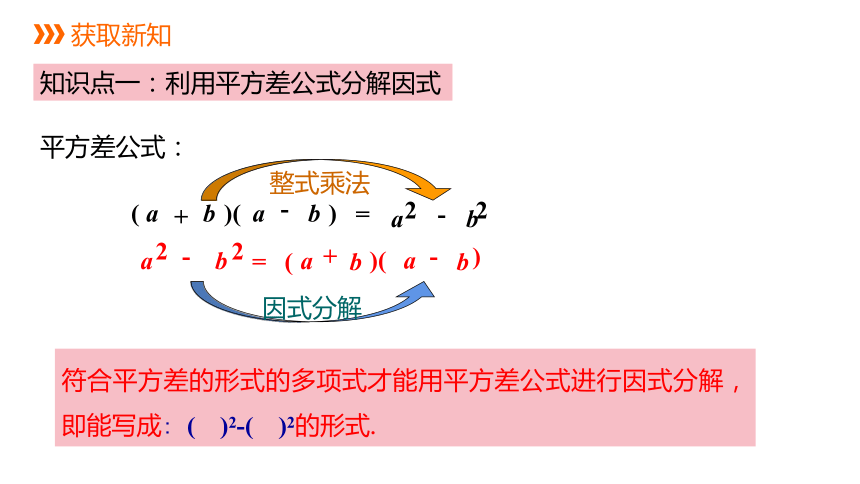
获取新知
知识点一:利用平方差公式分解因式
平方差公式:
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成:
(
)2-(
)2的形式.
例题讲解
例1
把下列各式分解因式:
(1)x2-81;
(2)36a2-25b2.
解:(1)
x2-81
=x2-92
=(x+9)(x-9).
(2)
36a2-25b2
=(6a)2-(5b)2
=(6a+5b)(6a-5b).
例2
分解因式:
(1)x2y-4y;(2)(a+1)2-1;
(3)x4-1;
(4)(x+y+z)2-(x-y+z)2.
分析:对于(1)可先提取公因式,再利用平方差公式分解因式;
对于(2)将(a+1)视为一个整体运用平方差公式分解因式;
对于(3)分解因式要完全;
对于(4)分别将(x+y+z)与(x-y+z)视为整体,运用平方差公式进行分解因式.
解:(1)原式=y(x2-22)=y(x+2)(x-2).
(2)原式=(a+1)2-12=(a+1+1)(a+1-1)=a(a+2).
(3)原式=(x2)2-12=(x2+1)(x2-12)=(x2+1)(x+1)(x-1).
(4)原式=[(x+y+z)+(x-y+z)][(x+y+z)-(x-y+z)]
=(x+y+z+x-y+z)(x+y+z-x+y-z)
=2y(2x+2z)
=4y(x+z).
例3
计算下列各题:
(1)1012-992;
(2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4×(53.52-46.52)
=4(53.5+46.5)×(53.5-46.5)
=4×100×7=2800.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
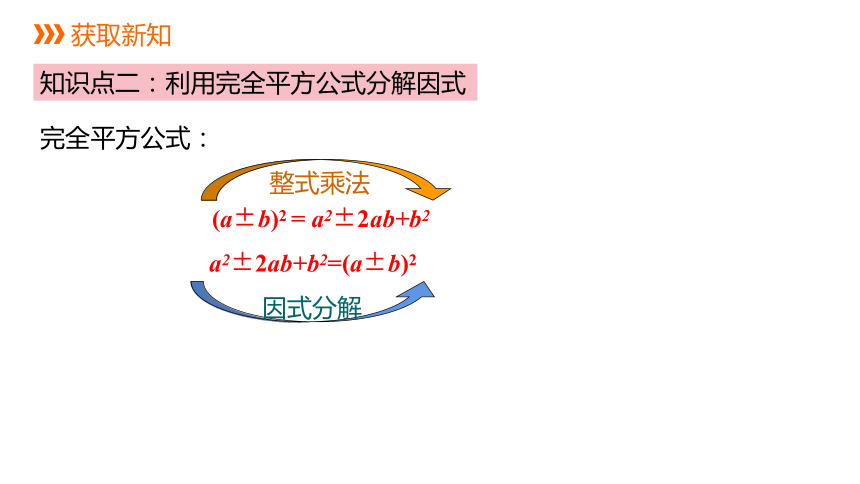
获取新知
知识点二:利用完全平方公式分解因式
完全平方公式:
整式乘法
因式分解
(a±b)2
=
a2±2ab+b2
a2±2ab+b2=(a±b)2
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
例题讲解
例4
把下列各式分解因式:
(1)x2+14x+49;
(2)9a2-30ab+25b2.
解:(1)x2+14x+49
=x2+2·x·7+72
=(x+7)2.
(2)
9a2-30ab+25b2
=(3a)2-2×3a×5b+(5b)2
=(3a-5b)2.
例5
分解因式:
(1)
-2x3y+4x2y-2xy;(3)(a-b)2-6(b-a)+9;(4)(x2-2x)2+2(x2-2x)+1.
分析:对于(1)先提取公因式-2xy后,再运用完全平方公式进行因式分解;
对于(2)将(b-a)化为-(a-b)后,再运用完全平方公式进行因式分解;
对于(3)可视(x2-2x)为一个整体,再运用完全平方公式进行因式分解.
解:(1)原式=-2xy(x2-2x+1)=-2xy(x-1)2.
(2)原式=(a-b)2+2(a-b)×3+32=(a-b+3)2.
(3)原式=(x2-2x)2+2(x2-2x)×1+12
=(x2-2x+1)2=[(x-1)2]2
=(x-1)4.
例6
把下列完全平方公式分解因式:
(1)1002-2×100×99+99?;
(2)342+34×32+162.
解:(1)原式=(100-99)?=1.
(2)原式=(34+16)2=2500.
本题利用完全平方公式分解因式,可以简化计算
例7
分解因式:
(1)ab2-ac2;
(2)3ax2+24axy+48ay2.
(2)3ax2+24axy+48ay2
=3a(x2+8xy+16y2)(提取公因式)
=3a(x+4y)2.(用完全平方公式)
解:(1)ab2-ac2
=a(b2-c2)(提取公因式)
=a(b+c)(b-c).(用平方差公式)
分解因式的方法步骤:一提(公因式)、二套(公式)、三查(是否分解彻底)
随堂演练
1.下列多项式中能用平方差公式分解因式的是( )
A.-a2+b2
B.-a2-b2
C.a2+b2
D.y2+x
A
2.多项式x2-kx+9能用完全平方公式分解因式,
则k的值为( )
A.±3
B.3
C.±6
D.6
C
3.分解因式(2x+3)2
-x2的结果是( )
A.3(x2+4x+3)
B.3(x2+2x+3)
C.(3x+3)(x+3)
D.3(x+1)(x+3)
D
4.
下列因式分解正确的是( )
A.a4b-6a3b+9a2b=a2b(a2-6a+9)
B.x2-x+
C.x2-2x+4=(x-2)2
D.4x2-y2=(4x+y)(4x-y)
B
5.
利用1个a×a的正方形,1个b×b的正方形和2个a×b的长方形可拼成一个正方形(如图所示),从而可得到一个含字母a,b的关于因式分解的公式是__________________.
a2+2ab+b2=(a+b)2
6.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_______.
4
7.分解因式:
(1)1-25b2;(2)(x+y)2-(x-y)2;(3)25(a+b)2-9(a-b)2;
(4)9x2+6x+1;
(5)a2-4ab+4b2;(6)
y2+2y+1-x2
解:(1)1-25b2
=1-(5b)2
=(1+5b)(1-5b).
(2)(x+y)2-(x-y)2
=(x+y+x-y)(x+y-x+y)
=4xy.
(3)25(a+b)2-9(a-b)2
=[5(a+b)]2-[3(a-b)]2
=[5(a+b)+3(a-b)][5(a+b)-3(a-b)]
=(8a+2b)(2a+8b)
=4(4a+b)(a+4b).
(4)9x2+6x+1
=(3x)2+2?3x?1+12
=(3x+1)2
(5)a2-4ab+4b2
=a2-2?a?2b+(2b)2
=(a-2b)2.
(6)
y2+2y+1-x2
=(y+1)?
-x?
=(y+1+x)(y+1-x).
课堂小结
公式法因式分解
公式
平方差公式a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
完全平方公a2±2ab+b2=(a±b)2
第8章
整式乘法与因式分解
8.4
第2课时
公式法
知识回顾
1.整式的乘法:
整式的乘积
因式分解:
多项式
多项式
整式的乘积
2.因式分解:提公因式法
实质:乘法分配律的逆用
步骤:一找;二提
获取新知
知识点一:利用平方差公式分解因式
平方差公式:
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
符合平方差的形式的多项式才能用平方差公式进行因式分解,即能写成:
(
)2-(
)2的形式.
例题讲解
例1
把下列各式分解因式:
(1)x2-81;
(2)36a2-25b2.
解:(1)
x2-81
=x2-92
=(x+9)(x-9).
(2)
36a2-25b2
=(6a)2-(5b)2
=(6a+5b)(6a-5b).
例2
分解因式:
(1)x2y-4y;(2)(a+1)2-1;
(3)x4-1;
(4)(x+y+z)2-(x-y+z)2.
分析:对于(1)可先提取公因式,再利用平方差公式分解因式;
对于(2)将(a+1)视为一个整体运用平方差公式分解因式;
对于(3)分解因式要完全;
对于(4)分别将(x+y+z)与(x-y+z)视为整体,运用平方差公式进行分解因式.
解:(1)原式=y(x2-22)=y(x+2)(x-2).
(2)原式=(a+1)2-12=(a+1+1)(a+1-1)=a(a+2).
(3)原式=(x2)2-12=(x2+1)(x2-12)=(x2+1)(x+1)(x-1).
(4)原式=[(x+y+z)+(x-y+z)][(x+y+z)-(x-y+z)]
=(x+y+z+x-y+z)(x+y+z-x+y-z)
=2y(2x+2z)
=4y(x+z).
例3
计算下列各题:
(1)1012-992;
(2)53.52×4-46.52×4.
解:(1)原式=(101+99)(101-99)=400;
(2)原式=4×(53.52-46.52)
=4(53.5+46.5)×(53.5-46.5)
=4×100×7=2800.
方法总结:较为复杂的有理数运算,可以运用因式分解对其进行变形,使运算得以简化.
获取新知
知识点二:利用完全平方公式分解因式
完全平方公式:
整式乘法
因式分解
(a±b)2
=
a2±2ab+b2
a2±2ab+b2=(a±b)2
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
例题讲解
例4
把下列各式分解因式:
(1)x2+14x+49;
(2)9a2-30ab+25b2.
解:(1)x2+14x+49
=x2+2·x·7+72
=(x+7)2.
(2)
9a2-30ab+25b2
=(3a)2-2×3a×5b+(5b)2
=(3a-5b)2.
例5
分解因式:
(1)
-2x3y+4x2y-2xy;(3)(a-b)2-6(b-a)+9;(4)(x2-2x)2+2(x2-2x)+1.
分析:对于(1)先提取公因式-2xy后,再运用完全平方公式进行因式分解;
对于(2)将(b-a)化为-(a-b)后,再运用完全平方公式进行因式分解;
对于(3)可视(x2-2x)为一个整体,再运用完全平方公式进行因式分解.
解:(1)原式=-2xy(x2-2x+1)=-2xy(x-1)2.
(2)原式=(a-b)2+2(a-b)×3+32=(a-b+3)2.
(3)原式=(x2-2x)2+2(x2-2x)×1+12
=(x2-2x+1)2=[(x-1)2]2
=(x-1)4.
例6
把下列完全平方公式分解因式:
(1)1002-2×100×99+99?;
(2)342+34×32+162.
解:(1)原式=(100-99)?=1.
(2)原式=(34+16)2=2500.
本题利用完全平方公式分解因式,可以简化计算
例7
分解因式:
(1)ab2-ac2;
(2)3ax2+24axy+48ay2.
(2)3ax2+24axy+48ay2
=3a(x2+8xy+16y2)(提取公因式)
=3a(x+4y)2.(用完全平方公式)
解:(1)ab2-ac2
=a(b2-c2)(提取公因式)
=a(b+c)(b-c).(用平方差公式)
分解因式的方法步骤:一提(公因式)、二套(公式)、三查(是否分解彻底)
随堂演练
1.下列多项式中能用平方差公式分解因式的是( )
A.-a2+b2
B.-a2-b2
C.a2+b2
D.y2+x
A
2.多项式x2-kx+9能用完全平方公式分解因式,
则k的值为( )
A.±3
B.3
C.±6
D.6
C
3.分解因式(2x+3)2
-x2的结果是( )
A.3(x2+4x+3)
B.3(x2+2x+3)
C.(3x+3)(x+3)
D.3(x+1)(x+3)
D
4.
下列因式分解正确的是( )
A.a4b-6a3b+9a2b=a2b(a2-6a+9)
B.x2-x+
C.x2-2x+4=(x-2)2
D.4x2-y2=(4x+y)(4x-y)
B
5.
利用1个a×a的正方形,1个b×b的正方形和2个a×b的长方形可拼成一个正方形(如图所示),从而可得到一个含字母a,b的关于因式分解的公式是__________________.
a2+2ab+b2=(a+b)2
6.若将(2x)n-81分解成(4x2+9)(2x+3)(2x-3),则n的值是_______.
4
7.分解因式:
(1)1-25b2;(2)(x+y)2-(x-y)2;(3)25(a+b)2-9(a-b)2;
(4)9x2+6x+1;
(5)a2-4ab+4b2;(6)
y2+2y+1-x2
解:(1)1-25b2
=1-(5b)2
=(1+5b)(1-5b).
(2)(x+y)2-(x-y)2
=(x+y+x-y)(x+y-x+y)
=4xy.
(3)25(a+b)2-9(a-b)2
=[5(a+b)]2-[3(a-b)]2
=[5(a+b)+3(a-b)][5(a+b)-3(a-b)]
=(8a+2b)(2a+8b)
=4(4a+b)(a+4b).
(4)9x2+6x+1
=(3x)2+2?3x?1+12
=(3x+1)2
(5)a2-4ab+4b2
=a2-2?a?2b+(2b)2
=(a-2b)2.
(6)
y2+2y+1-x2
=(y+1)?
-x?
=(y+1+x)(y+1-x).
课堂小结
公式法因式分解
公式
平方差公式a2-b2=(a+b)(a-b)
步骤
一提:公因式;
二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
完全平方公a2±2ab+b2=(a±b)2
