2020-2021学年人教版八年级数学下册课件-18.2.2 菱形(共15张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册课件-18.2.2 菱形(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 18:15:01 | ||
图片预览






文档简介
(共15张PPT)
18.2特殊的平行四边形
18.2.2菱形
平行四边形的性质
边
平行四边形的两组对边分别平行,且相等;
角
平行四边形的两组对角分别相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
矩形的性质
矩形的四个角都是直角
矩形的对角线相等
情景创设
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?
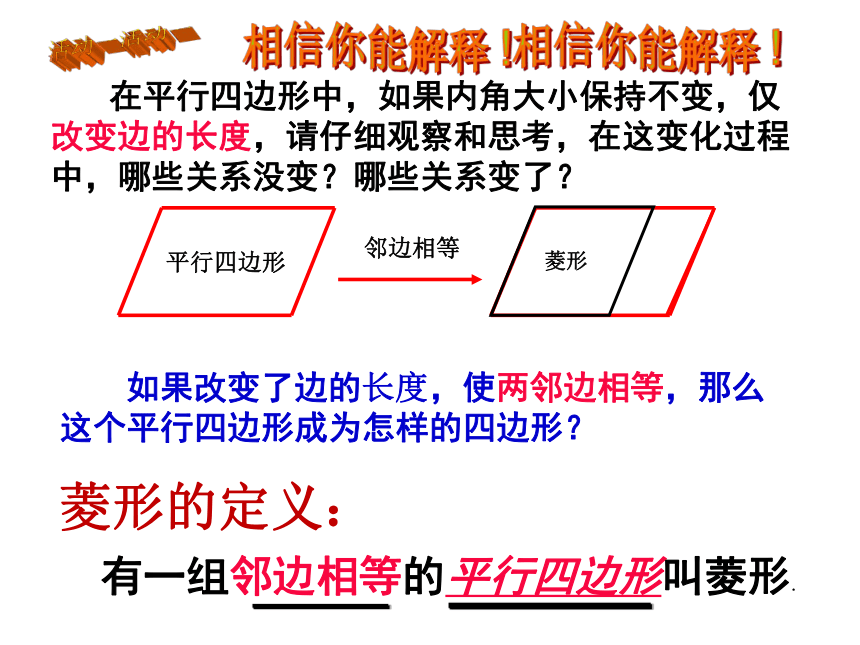
有一组邻边相等的平行四边形叫菱形.
平行四边形
邻边相等
菱形
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?
活动一
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
相信你能解释
!
菱形的定义:
感受生活
你能举出生活中你看到的菱形吗?
活动二:折一折
剪一剪
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1、菱形是轴对称图形吗?
2、菱形有几条对称轴?
3、对称轴之间有什么关系?
菱形的
两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的性质
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴
AD
BC
AB
CD
∥
=
∴
AB=BC=CD=DA
∴
∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴
OA=OC;OB=OD
∴
∠DAB=∠DCB
∠ADC=∠ABC
∴
∠DAB+∠ABC=
180°
A
B
C
D
O
例1:四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴
BD=2OB=6
cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
学以致用
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60°,则∠BAC=_______.
3cm
60°
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是(
)
A
B
C
D
O
C
A.10cm
B.7cm
C.
5cm
D.4cm
课堂小结:
菱形
定义
有一组邻边相等的平行四边形
性
质
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
作业:课本P57
练习
1
18.2特殊的平行四边形
18.2.2菱形
平行四边形的性质
边
平行四边形的两组对边分别平行,且相等;
角
平行四边形的两组对角分别相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
矩形的性质
矩形的四个角都是直角
矩形的对角线相等
情景创设
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形?
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?
有一组邻边相等的平行四边形叫菱形.
平行四边形
邻边相等
菱形
在平行四边形中,如果内角大小保持不变,仅改变边的长度,请仔细观察和思考,在这变化过程中,哪些关系没变?哪些关系变了?
活动一
如果改变了边的长度,使两邻边相等,那么这个平行四边形成为怎样的四边形?
相信你能解释
!
菱形的定义:
感受生活
你能举出生活中你看到的菱形吗?
活动二:折一折
剪一剪
有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
画出菱形的两条折痕,并通过折叠手中的图形回答以下问题:
1、菱形是轴对称图形吗?
2、菱形有几条对称轴?
3、对称轴之间有什么关系?
菱形的
两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的性质
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
并且每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴
AD
BC
AB
CD
∥
=
∴
AB=BC=CD=DA
∴
∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴
OA=OC;OB=OD
∴
∠DAB=∠DCB
∠ADC=∠ABC
∴
∠DAB+∠ABC=
180°
A
B
C
D
O
例1:四边形ABCD是菱形,O是两条对角线的交点,已知AB=5cm,AO=4cm,求对角线BD的长。
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴
BD=2OB=6
cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
学以致用
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60°,则∠BAC=_______.
3cm
60°
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是(
)
A
B
C
D
O
C
A.10cm
B.7cm
C.
5cm
D.4cm
课堂小结:
菱形
定义
有一组邻边相等的平行四边形
性
质
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
作业:课本P57
练习
1
