2020—2021学年人教版数学七年级下册8.2消元----解二元一次方程组课件(共18张ppt)
文档属性
| 名称 | 2020—2021学年人教版数学七年级下册8.2消元----解二元一次方程组课件(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
8.2二元一次方程组的解法
—加减消元法
一元
代入求解:消去一个未知数后变成一元一次方程,求出一个未知数的值;
回代求解:把求得的未知数的值代回到变形的方程中,求出另一个未知数的值;
写解:用
变形:选择其中一个方程,把它变形用一个未知数的式子去表示另一个未知数的形式;
消元:
二元
2、解二元一次方程组的基本思路是什么?
3、用代入法解方程组的步骤是什么?
一元
1、根据等式性质填空:
(1)若a=b,那么a±c=
.
(2)若a=b,那么ac=
.
思考:若a=b,c=d,那么a+c=b+d吗?
b±c
bc
(等式性质1)
(等式性质2)
的形式写出方程组的解。
问题
用代入消元法解下面的二元一次方程组
代入消元法
①
②
解:由①得x=10-y
③
将③代入②得:y+2(10-y)
=
16
解得:y=4
将y=4代入①得
4+
x
=
10
x=6
所以方程组的解为:
1.会用加减消元法解二元一次方程组。
2.体会解二元一次方程组的基本思想——“消元”。
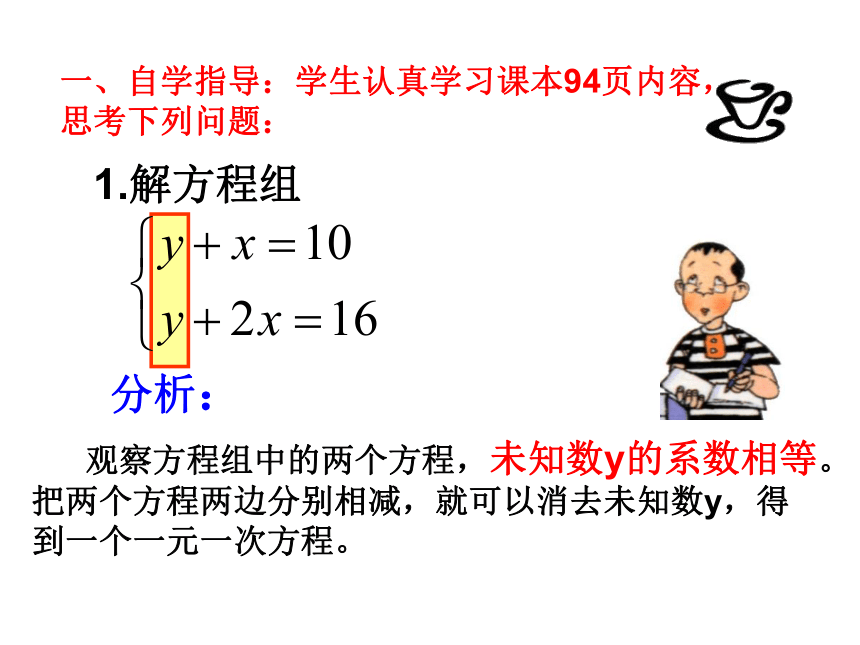
观察方程组中的两个方程,未知数y的系数相等。把两个方程两边分别相减,就可以消去未知数y,得到一个一元一次方程。
分析:
1.解方程组
一、自学指导:学生认真学习课本94页内容,思考下列问题:
解:由②-①,得
(2x+y)-(x+y)
=16-10
把y=4代入①,得
x+4=10
所以这个方程组的解是
解得
y=4
解二元一次方程组:
x+
y=10
①
2x+y=16
②
y=4
x=6
解得
x=6
解:由①+②,得
把x=2代入①,得
y=3
x=2
所以这个方程组的解是
5x=10
2.解二元一次方程组:
3x+5y=21
①
2x-5y=-11
②
y=3
x=2
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法.
由①+②,得
5x=10
2x-5y=7
①
2x+3y=-1
②
由
②-①,得
8y=-8
第三站——感悟之旅
3x-5y=21
①
2x+5y=-11
②
加减消元法:
通过把两个方程相加或相减消去一个未知数,转化为一元一次方程.
(1)当同一个未知数的系数相同时,用_____法消元;
(2)当同一个未知数的系数互为相反数时,用_____法
消元。
减
加
议一议
方程组的这种解法与代入法解方程组有什么不同点呢?
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数
x
一.填空题:
只要两边
只要两边
②
②
二.选择题
1.
用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用(
)
A.①-②消去y
B.①-②消去x
C.
②-
①消去常数项
D.
以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是(
)
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
②
三.指出下列方程组求解过程中是否有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x
=-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x
=2
5u+2v=-4
3u-4v=-18
①
②
例1解方程组:
10u+4v=-8③
解:①×2,得
将u=-2代入方程①,得
(-2)×5+2v=-4
解得
u=-2
v=3
②
+
③
,得
13u=-26
解这个一元一次方程,得
加减消元法一般步骤:
u
=-2
v=3
所以这个方程组的解是
(1)变形使方程组两个方程中某一未知数的系数相等或互为相反数
(2)加减消去一个未知数,得关于另一个未知数的一元一次方程
(3)解这个一元一次方程,求得一个未知数的值
(4)把求得的未知数的值代入方
程组中任意一个方程,即可得另一个未知数的值.
(5)作结论
变形
消元
求解
代入
写解
用加减法解方程组:
①
②
2x-3y=4
3x+6y=6
做一做
知识应用拓展升华
例2解方程组
3x+
4y
=
16
5x
-
6y
=
33
解:
①
×3
,得
19x
=
114
把x
=
6代入①,得
所以这个方程组的解为
即
x
=
6
18
+
4y
=
16
9x+
12y
=
48
②
×2,
得
10x
-
12y
=
66
③
+
④,
得
y
=
x
=
6
1
2
即
y
=
1
2
④
③
①
②
点悟:当未知数的系数没有倍数关系,则应将两个方程同时变形,同时选择系数绝对值比较小的未知数消元。
用加减法解下列方程组
4s+3t=5
2s-t=-5
(1)
(2)
5x-6y=9
7x-4y=-5
基本思想:
前提条件:
加减消元:
二元
一元
1.加减消元法解方程组基本思想是什么?
2.加减消元法解方程组前提条件是什么?
相同未知数的系数相等或互为相反数
系数相同
相减
系数互为相反数
相加
学习了本节课你有哪些收获?
3、用加减法解二元一次方程组的步骤:
变形
消元
求解
写解
代入
8.2二元一次方程组的解法
—加减消元法
一元
代入求解:消去一个未知数后变成一元一次方程,求出一个未知数的值;
回代求解:把求得的未知数的值代回到变形的方程中,求出另一个未知数的值;
写解:用
变形:选择其中一个方程,把它变形用一个未知数的式子去表示另一个未知数的形式;
消元:
二元
2、解二元一次方程组的基本思路是什么?
3、用代入法解方程组的步骤是什么?
一元
1、根据等式性质填空:
(1)若a=b,那么a±c=
.
(2)若a=b,那么ac=
.
思考:若a=b,c=d,那么a+c=b+d吗?
b±c
bc
(等式性质1)
(等式性质2)
的形式写出方程组的解。
问题
用代入消元法解下面的二元一次方程组
代入消元法
①
②
解:由①得x=10-y
③
将③代入②得:y+2(10-y)
=
16
解得:y=4
将y=4代入①得
4+
x
=
10
x=6
所以方程组的解为:
1.会用加减消元法解二元一次方程组。
2.体会解二元一次方程组的基本思想——“消元”。
观察方程组中的两个方程,未知数y的系数相等。把两个方程两边分别相减,就可以消去未知数y,得到一个一元一次方程。
分析:
1.解方程组
一、自学指导:学生认真学习课本94页内容,思考下列问题:
解:由②-①,得
(2x+y)-(x+y)
=16-10
把y=4代入①,得
x+4=10
所以这个方程组的解是
解得
y=4
解二元一次方程组:
x+
y=10
①
2x+y=16
②
y=4
x=6
解得
x=6
解:由①+②,得
把x=2代入①,得
y=3
x=2
所以这个方程组的解是
5x=10
2.解二元一次方程组:
3x+5y=21
①
2x-5y=-11
②
y=3
x=2
当二元一次方程组的两个方程中同一未知数的系数相反或相等时,把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法.
由①+②,得
5x=10
2x-5y=7
①
2x+3y=-1
②
由
②-①,得
8y=-8
第三站——感悟之旅
3x-5y=21
①
2x+5y=-11
②
加减消元法:
通过把两个方程相加或相减消去一个未知数,转化为一元一次方程.
(1)当同一个未知数的系数相同时,用_____法消元;
(2)当同一个未知数的系数互为相反数时,用_____法
消元。
减
加
议一议
方程组的这种解法与代入法解方程组有什么不同点呢?
分别相加
y
1.已知方程组
x+3y=17
2x-3y=6
两个方程
就可以消去未知数
分别相减
2.已知方程组
25x-7y=16
25x+6y=10
两个方程
就可以消去未知数
x
一.填空题:
只要两边
只要两边
②
②
二.选择题
1.
用加减法解方程组
6x+7y=-19①
6x-5y=17②
应用(
)
A.①-②消去y
B.①-②消去x
C.
②-
①消去常数项
D.
以上都不对
B
2.方程组
3x+2y=13
3x-2y=5
消去y后所得的方程是(
)
B
A.6x=8
B.6x=18
C.6x=5
D.x=18
②
三.指出下列方程组求解过程中是否有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解:①-②,得
-2x=12
x
=-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x
=2
5u+2v=-4
3u-4v=-18
①
②
例1解方程组:
10u+4v=-8③
解:①×2,得
将u=-2代入方程①,得
(-2)×5+2v=-4
解得
u=-2
v=3
②
+
③
,得
13u=-26
解这个一元一次方程,得
加减消元法一般步骤:
u
=-2
v=3
所以这个方程组的解是
(1)变形使方程组两个方程中某一未知数的系数相等或互为相反数
(2)加减消去一个未知数,得关于另一个未知数的一元一次方程
(3)解这个一元一次方程,求得一个未知数的值
(4)把求得的未知数的值代入方
程组中任意一个方程,即可得另一个未知数的值.
(5)作结论
变形
消元
求解
代入
写解
用加减法解方程组:
①
②
2x-3y=4
3x+6y=6
做一做
知识应用拓展升华
例2解方程组
3x+
4y
=
16
5x
-
6y
=
33
解:
①
×3
,得
19x
=
114
把x
=
6代入①,得
所以这个方程组的解为
即
x
=
6
18
+
4y
=
16
9x+
12y
=
48
②
×2,
得
10x
-
12y
=
66
③
+
④,
得
y
=
x
=
6
1
2
即
y
=
1
2
④
③
①
②
点悟:当未知数的系数没有倍数关系,则应将两个方程同时变形,同时选择系数绝对值比较小的未知数消元。
用加减法解下列方程组
4s+3t=5
2s-t=-5
(1)
(2)
5x-6y=9
7x-4y=-5
基本思想:
前提条件:
加减消元:
二元
一元
1.加减消元法解方程组基本思想是什么?
2.加减消元法解方程组前提条件是什么?
相同未知数的系数相等或互为相反数
系数相同
相减
系数互为相反数
相加
学习了本节课你有哪些收获?
3、用加减法解二元一次方程组的步骤:
变形
消元
求解
写解
代入
