2020-2021学年苏科版八年级下册第九章中心对称图形-平行四边形单元测试题三(word版无答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级下册第九章中心对称图形-平行四边形单元测试题三(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览

文档简介
第九章中心对称-平行四边形单元测试题三
一、选择题
1.如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )
A.40°
B.50°
C.70°
D.100°
2.如图,□ABCD的对角线AC与BD相交于点O,AB⊥CD.若,,则BD的长为(
)
A.
B.9
C.10
D.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=BC,则∠BCE的度数是(
)
A.22.5°
B.25°
C.23°
D.20
4.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是(
)
A.1<MN<5
B.1<MN≤5
C.<MN<
D.<MN≤
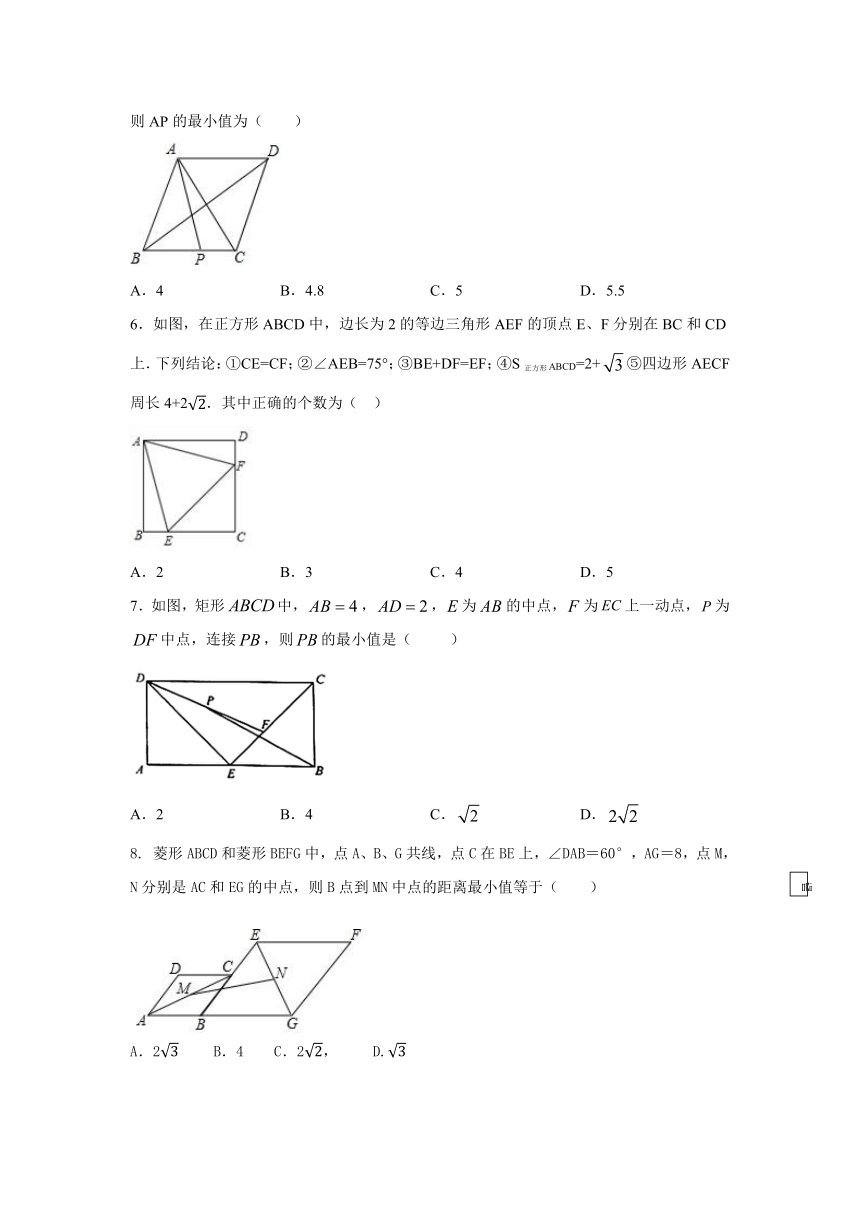
5.如图,菱形ABCD的两条对角线长分别为CD=6,BD=8,点P是BC边上的一动点,则AP的最小值为(
)
A.4
B.4.8
C.5
D.5.5
6.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+⑤四边形AECF周长4+2.其中正确的个数为(
)
A.2
B.3
C.4
D.5
7.如图,矩形中,,,为的中点,为上一动点,为中点,连接,则的最小值是(
)
A.2
B.4
C.
D.
8.
菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则B点到MN中点的距离最小值等于( )
A.2
B.4
C.2,
D.
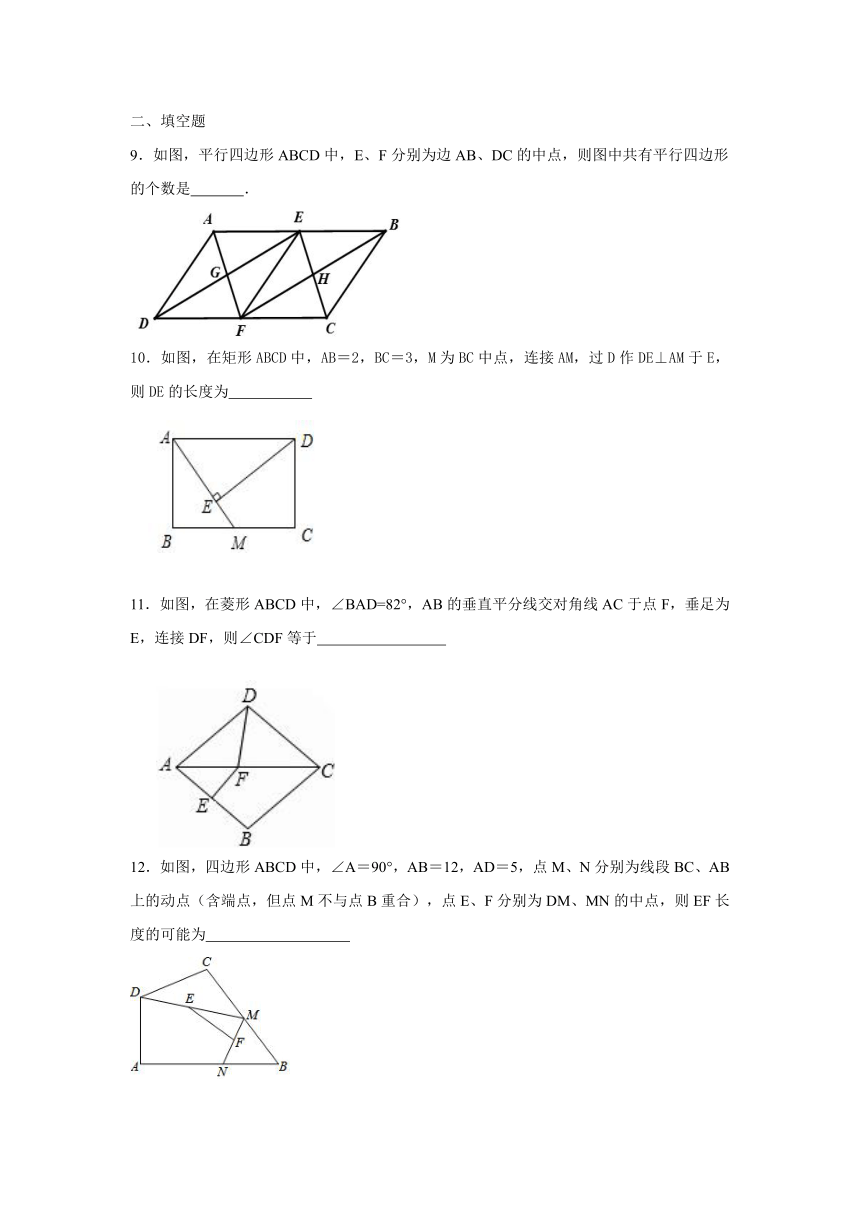
二、填空题
9.如图,平行四边形ABCD中,E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是
.
10.如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为
11.如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于
12.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为
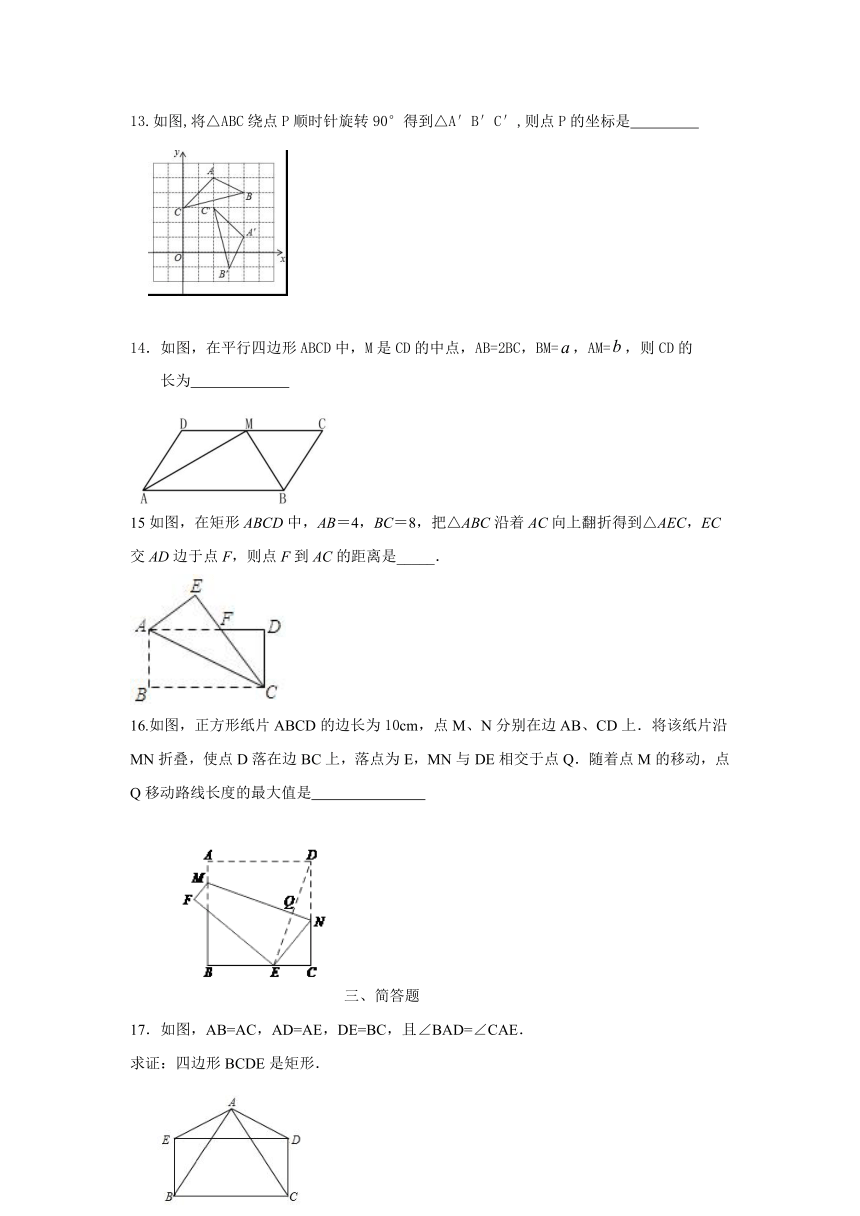
13.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=,AM=,则CD的
长为
15如图,在矩形ABCD中,AB=4,BC=8,把△ABC沿着AC向上翻折得到△AEC,EC交AD边于点F,则点F到AC的距离是_____.
16.如图,正方形纸片ABCD的边长为10cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是
简答题
17.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
18..如图,四边形ABCD中,∠ABC=90°,∠CAD=2∠CAB=45°,E、F分别是CD、CA的中点,AC=AD=8,求BE的长.
如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF,连接DE、BE、BF、DF.
(1)求证:四边形BEDF为菱形;
(2)若菱形BEDF的边长为2,AE=2,求正方形ABCD的边长.
20.如图,点A、B、C是4×
4网格上的格点,连接点A、B、C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.
(1)在图1中,在AC上找一点M,使;
(2)在图2中,在△ABC
内部(不含边界)找一点N,使.
21.A在直线l外,点B在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.
22.在矩形
ABCD
中,AB=3,BC=4,E、F
是对角线
AC
上的两个动点,分
别从
A、C
同时出发相向而行,速度均为每秒
1
个单位长度,运动时间为
t
秒,其中
0
t
5
.
(1)若
G,H
分别是
AB,DC
中点,求证:四边形
EGFH
是平行四边形(E、F
相遇时除外);
(2)在(1)条件下,若四边形
EGFH
为矩形,求
t
的值;
(3)若
G,H
分别是折线
A-B-C,C-D-A
上的动点,与
E,F
相同的速度同时出发,若
四边形
EGFH
为菱形,求
t
的值.
23.如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为
.
24.【定义学习】
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“互补四边形”.
【判断尝试】
在①梯形;②矩形;③菱形,④正方形中,是“互补四边形”的是 ▲ .(填序号)
【操作探究】
在?ABCD中,AB=5,BC=6,AE=4,
AE⊥BC于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F
组成的四边形为“互补四边形”,画出示意图,并填空.
F在边AD上时,
F在边CD上时,
直接写出EF的长为 ▲
直接写出
AF的长为 ▲
【实践应用】
某加工厂有一批四边形板材,形状如图所示,若AB3米,AD1米,∠C45°,∠A∠B90°.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“互补四边形”板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长.
一、选择题
1.如图,把△ABC绕点C顺时针旋转某个角度θ得到△A′B′C,∠A=30°,∠1=70°,则旋转角θ可能等于( )
A.40°
B.50°
C.70°
D.100°
2.如图,□ABCD的对角线AC与BD相交于点O,AB⊥CD.若,,则BD的长为(
)
A.
B.9
C.10
D.
3.如图,四边形ABCD是正方形,延长AB到点E,使AE=BC,则∠BCE的度数是(
)
A.22.5°
B.25°
C.23°
D.20
4.已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是(
)
A.1<MN<5
B.1<MN≤5
C.<MN<
D.<MN≤
5.如图,菱形ABCD的两条对角线长分别为CD=6,BD=8,点P是BC边上的一动点,则AP的最小值为(
)
A.4
B.4.8
C.5
D.5.5
6.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+⑤四边形AECF周长4+2.其中正确的个数为(
)
A.2
B.3
C.4
D.5
7.如图,矩形中,,,为的中点,为上一动点,为中点,连接,则的最小值是(
)
A.2
B.4
C.
D.
8.
菱形ABCD和菱形BEFG中,点A、B、G共线,点C在BE上,∠DAB=60°,AG=8,点M,N分别是AC和EG的中点,则B点到MN中点的距离最小值等于( )
A.2
B.4
C.2,
D.
二、填空题
9.如图,平行四边形ABCD中,E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是
.
10.如图,在矩形ABCD中,AB=2,BC=3,M为BC中点,连接AM,过D作DE⊥AM于E,则DE的长度为
11.如图,在菱形ABCD中,∠BAD=82°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于
12.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为
13.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=,AM=,则CD的
长为
15如图,在矩形ABCD中,AB=4,BC=8,把△ABC沿着AC向上翻折得到△AEC,EC交AD边于点F,则点F到AC的距离是_____.
16.如图,正方形纸片ABCD的边长为10cm,点M、N分别在边AB、CD上.将该纸片沿MN折叠,使点D落在边BC上,落点为E,MN与DE相交于点Q.随着点M的移动,点Q移动路线长度的最大值是
简答题
17.如图,AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE.
求证:四边形BCDE是矩形.
18..如图,四边形ABCD中,∠ABC=90°,∠CAD=2∠CAB=45°,E、F分别是CD、CA的中点,AC=AD=8,求BE的长.
如图,E,F是正方形ABCD的对角线AC上的两点,AE=CF,连接DE、BE、BF、DF.
(1)求证:四边形BEDF为菱形;
(2)若菱形BEDF的边长为2,AE=2,求正方形ABCD的边长.
20.如图,点A、B、C是4×
4网格上的格点,连接点A、B、C得△ABC,请分别在下列图中使用无刻度的直尺按要求画图.
(1)在图1中,在AC上找一点M,使;
(2)在图2中,在△ABC
内部(不含边界)找一点N,使.
21.A在直线l外,点B在直线l上.
(1)在l上求作一点C,在l外求作一点D,使得以A、B、C、D为顶点的四边形是菱形;(要求:用直尺和圆规作出所有大小不同的菱形)
(2)连接AB,若AB=5,且点A到直线l的距离为4,通过计算,找出(1)中面积最小的菱形.
22.在矩形
ABCD
中,AB=3,BC=4,E、F
是对角线
AC
上的两个动点,分
别从
A、C
同时出发相向而行,速度均为每秒
1
个单位长度,运动时间为
t
秒,其中
0
t
5
.
(1)若
G,H
分别是
AB,DC
中点,求证:四边形
EGFH
是平行四边形(E、F
相遇时除外);
(2)在(1)条件下,若四边形
EGFH
为矩形,求
t
的值;
(3)若
G,H
分别是折线
A-B-C,C-D-A
上的动点,与
E,F
相同的速度同时出发,若
四边形
EGFH
为菱形,求
t
的值.
23.如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为
.
24.【定义学习】
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“互补四边形”.
【判断尝试】
在①梯形;②矩形;③菱形,④正方形中,是“互补四边形”的是 ▲ .(填序号)
【操作探究】
在?ABCD中,AB=5,BC=6,AE=4,
AE⊥BC于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F
组成的四边形为“互补四边形”,画出示意图,并填空.
F在边AD上时,
F在边CD上时,
直接写出EF的长为 ▲
直接写出
AF的长为 ▲
【实践应用】
某加工厂有一批四边形板材,形状如图所示,若AB3米,AD1米,∠C45°,∠A∠B90°.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“互补四边形”板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
