2020-2021学年苏科版七年级数学下册 第7章平面图形的认识二 章末综合提升训练(word版含解析)
文档属性
| 名称 | 2020-2021学年苏科版七年级数学下册 第7章平面图形的认识二 章末综合提升训练(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 19:17:18 | ||
图片预览

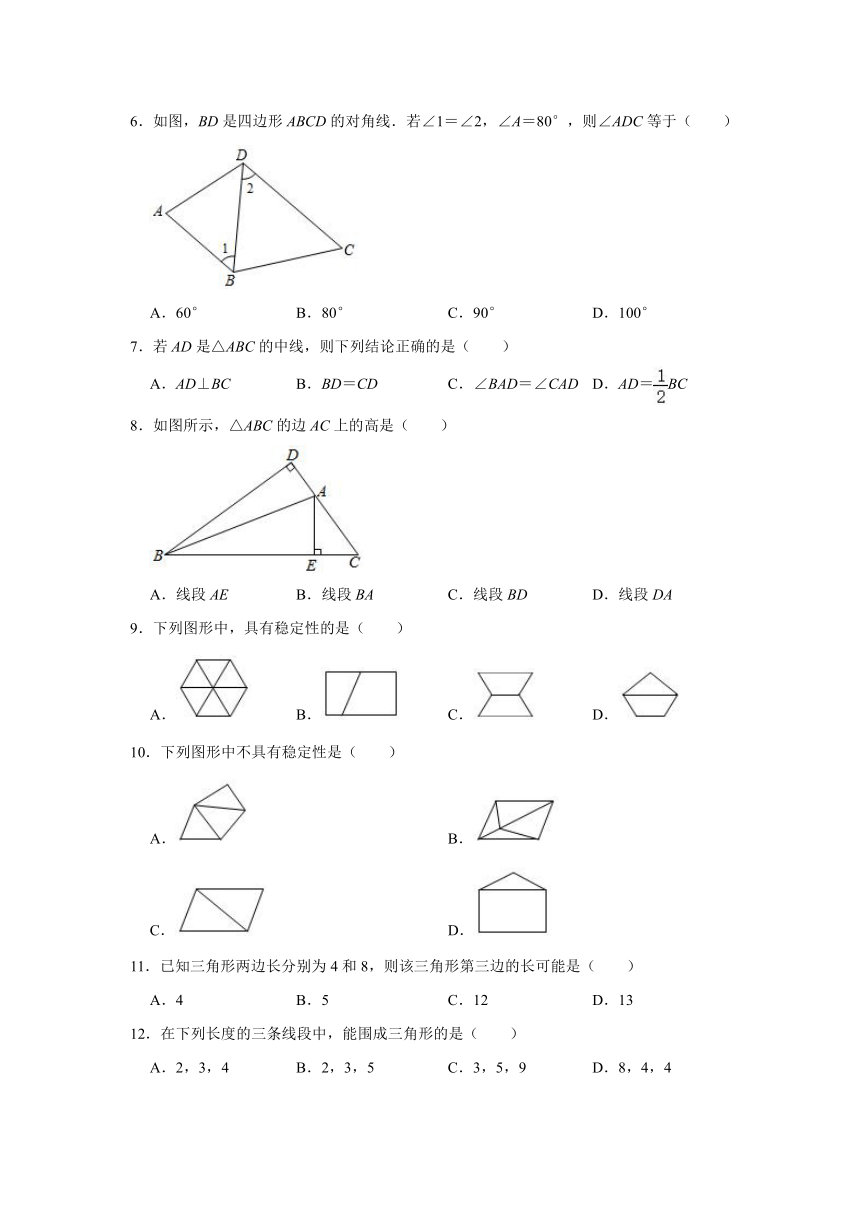
文档简介
2021年苏科版七年级数学下册《第7章平面图形的认识二》章末综合提升训练(附答案)
1.如图,点E在射线AB上,要AD∥BC,只需( )
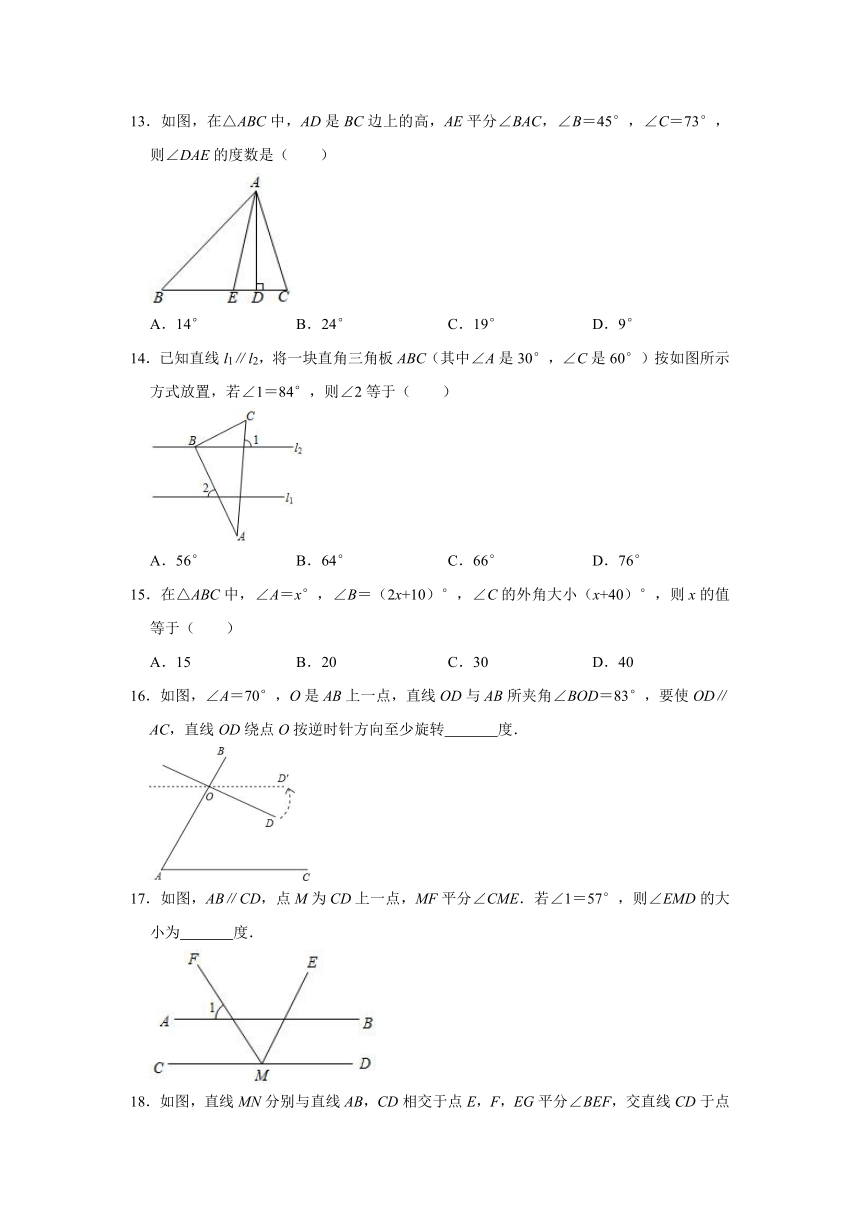
A.∠A=∠CBE
B.∠A=∠C
C.∠C=∠CBE
D.∠A+∠D=180°
2.如图,在下列给出的条件中,可以判定AB∥CD的有( )
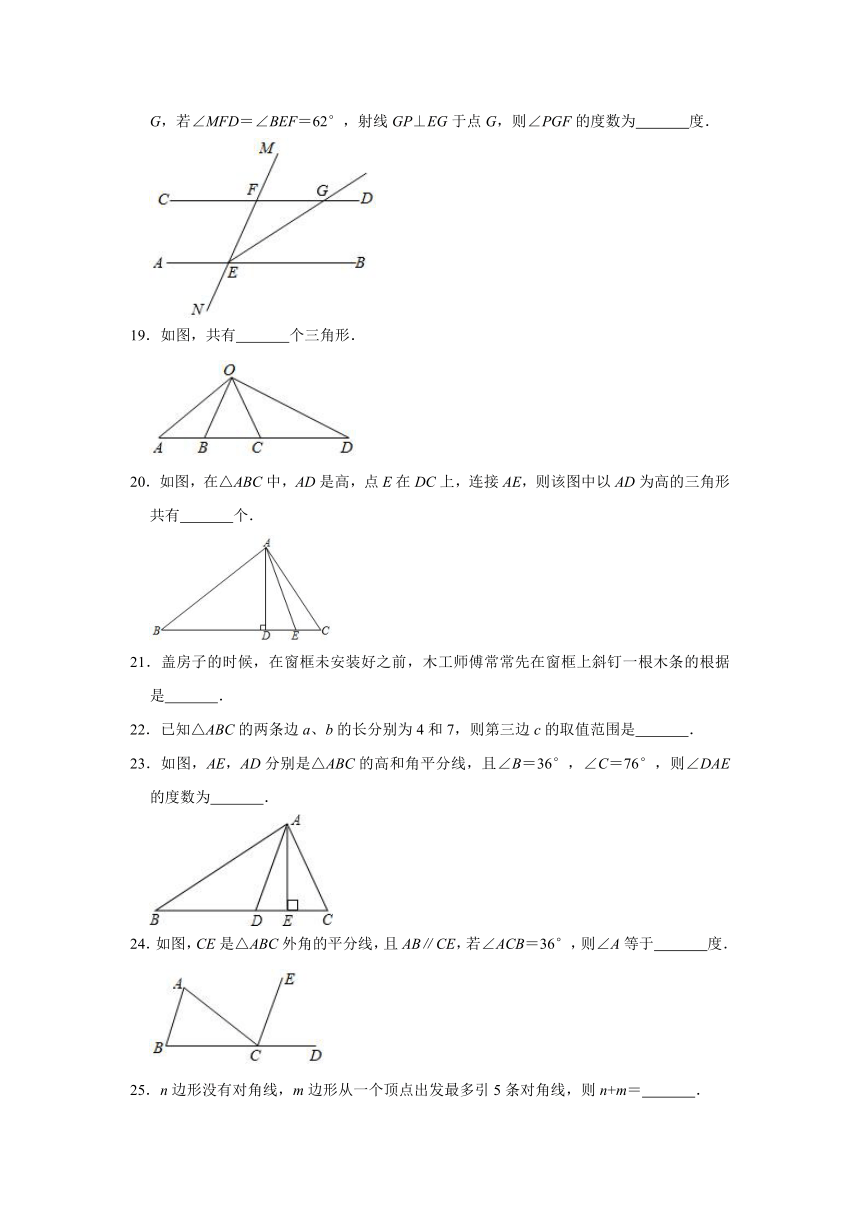
①∠1=∠2;②∠1=∠3;③∠2=∠4;④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③
B.①②④
C.①④⑤
D.②③⑤
3.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35°
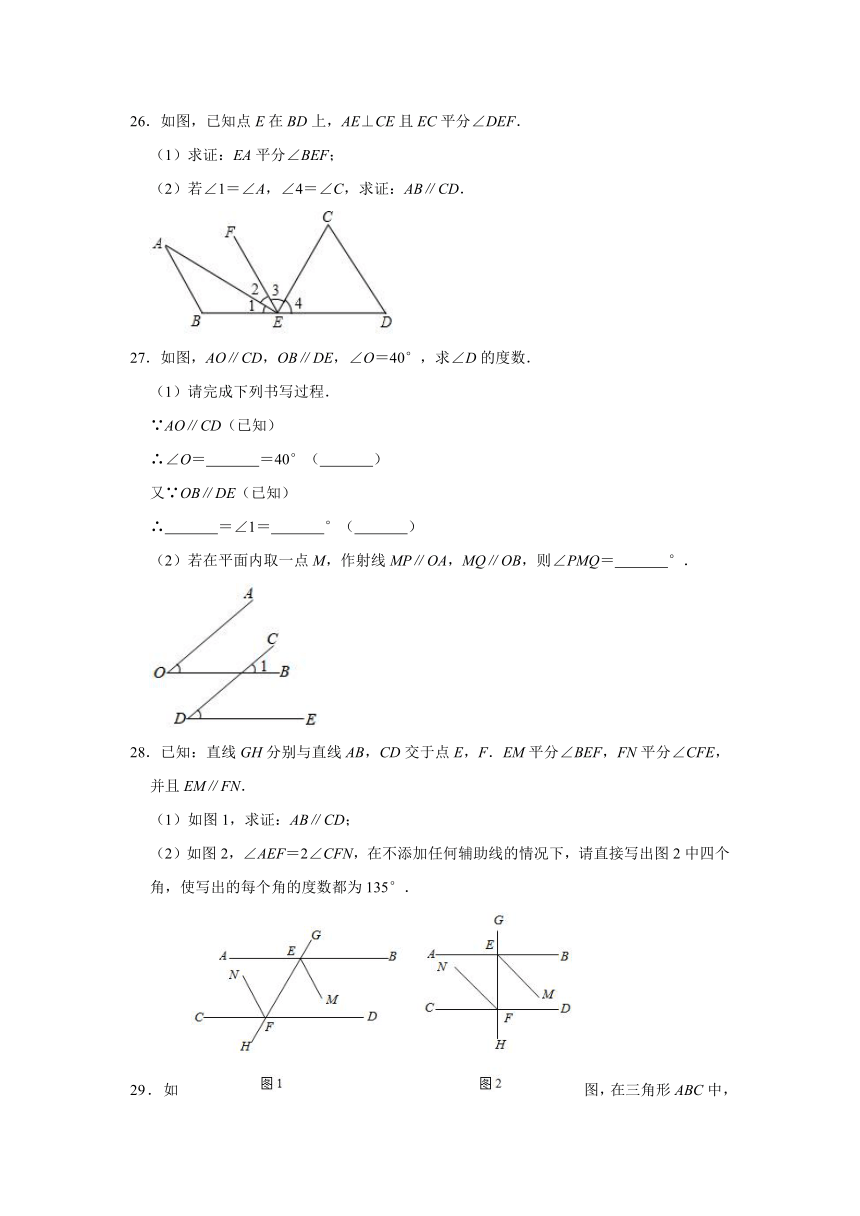
B.45°
C.50°
D.55°
4.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠2=∠3
5.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分∠ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
6.如图,BD是四边形ABCD的对角线.若∠1=∠2,∠A=80°,则∠ADC等于( )
A.60°
B.80°
C.90°
D.100°
7.若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
8.如图所示,△ABC的边AC上的高是( )
A.线段AE
B.线段BA
C.线段BD
D.线段DA
9.下列图形中,具有稳定性的是( )
A.
B.
C.
D.
10.下列图形中不具有稳定性是( )
A.
B.
C.
D.
11.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4
B.5
C.12
D.13
12.在下列长度的三条线段中,能围成三角形的是( )
A.2,3,4
B.2,3,5
C.3,5,9
D.8,4,4
13.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.14°
B.24°
C.19°
D.9°
14.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56°
B.64°
C.66°
D.76°
15.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小(x+40)°,则x的值等于( )
A.15
B.20
C.30
D.40
16.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=83°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转
度.
17.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为
度.
18.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为
度.
19.如图,共有
个三角形.
20.如图,在△ABC中,AD是高,点E在DC上,连接AE,则该图中以AD为高的三角形共有
个.
21.盖房子的时候,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条的根据是
.
22.已知△ABC的两条边a、b的长分别为4和7,则第三边c的取值范围是
.
23.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为
.
24.如图,CE是△ABC外角的平分线,且AB∥CE,若∠ACB=36°,则∠A等于
度.
25.n边形没有对角线,m边形从一个顶点出发最多引5条对角线,则n+m=
.
26.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
27.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
28.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
29.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
参考答案
1.解:要AD∥BC,只需∠A=∠CBE,
故选:A.
2.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
3.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
4.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
5.解:∵AD⊥BC,FG⊥BC,
∴∠FGD=∠ADB=90°,
∴FG∥AD,
故①正确;
∵DE∥AC,∠BAC=90°,
∴DE⊥AB,
不能证明DE为∠ADB的平分线,
故②错误;
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵DE⊥AB,
∴∠BAD+∠ADE=90°,
∴∠B=∠ADE,
故③正确;
∵∠BAC=90°,DE⊥AB,
∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,
∴∠CFG+∠BDE=90°,
故④正确,
综上所述,正确的选项①③④,
故选:C.
6.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=80°,
∴∠ADC=180°﹣80°=100°,
故选:D.
7.解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
8.解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
9.解:A、具有稳定性,故此选项符合题意;
B、不具有稳定性,故此选项不符合题意;
C、不具有稳定性,故此选项不符合题意;
D、不具有稳定性,故此选项不符合题意;
故选:A.
10.解:A、具有稳定性,故此选项不合题意;
B、具有稳定性,故此选项不符合题意;
C、具有稳定性,故此选项不合题意;
D、不具有稳定性,故此选项符合题意;
故选:D.
11.解:设第三边的长为x,
∵三角形两边的长分别是4和8,
∴8﹣4<x<8+4,即4<x<12,
只有5有可能,
故选:B.
12.解:根据三角形的三边关系,
A、2+3>4,能组成三角形,符合题意;
B、2+3=5,不能够组成三角形,不符合题意;
C、3+5=8<9,不能组成三角形,不符合题意;
D、4+4=8,不能组成三角形,不符合题意.
故选:A.
13.解:在△ABC中,∠B=45°,∠C=73°,
∴∠BAC=180°﹣∠B﹣∠C=62°.
∵AE平分∠BAC,
∴∠CAE=∠BAC=31°.
∵AD是BC边上的高,
∴AD⊥BC,
∴∠CAD=90°﹣∠C=17°,
∴∠DAE=∠CAE﹣∠CAD=31°﹣17°=14°.
故选:A.
14.解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
15.解:∵∠C的外角=∠A+∠B,
∴x+40=2x+10+x,
解得x=15.
故选:A.
16.解:∵OD'∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=83°﹣70°=13°.
故答案为:13.
17.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
18.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
19.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
20.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
21.解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性;
故答案为:三角形具有稳定性.
22.解:三角形两边的和>第三边,两边的差<第三边.
则7﹣4<c<7+4,
即3<c<11.
故答案为:3<c<11.
23.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
24.解:∵∠ACB=36°,
∴∠ACD=180°﹣∠ACB=180°﹣36°=144°,
∵CE是△ABC外角的平分线,
∴∠ACE=,
∵AB∥CE,
∴∠A=∠ACE=72°,
故答案为:72.
25.解:由题意得:m﹣3=5,n=3,
解得m=8,n=3,
∴m+n=8+3=11.
故答案为:11.
26.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
27.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
28.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
29.解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x
cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
1.如图,点E在射线AB上,要AD∥BC,只需( )
A.∠A=∠CBE
B.∠A=∠C
C.∠C=∠CBE
D.∠A+∠D=180°
2.如图,在下列给出的条件中,可以判定AB∥CD的有( )
①∠1=∠2;②∠1=∠3;③∠2=∠4;④∠DAB+∠ABC=180°;
⑤∠BAD+∠ADC=180°.
A.①②③
B.①②④
C.①④⑤
D.②③⑤
3.如图,直线AB∥CD,AE⊥CE,∠1=125°,则∠C等于( )
A.35°
B.45°
C.50°
D.55°
4.如图,若AD∥BC,则下列结论正确的是( )
A.∠1=∠3
B.∠2=∠4
C.∠1=∠2
D.∠2=∠3
5.如图,已知AD⊥BC,FG⊥BC,∠BAC=90°,DE∥AC.则结论:①FG∥AD;②DE平分∠ADB;③∠B=∠ADE;④∠CFG+∠BDE=90°.正确的是( )
A.①②③
B.①②④
C.①③④
D.②③④
6.如图,BD是四边形ABCD的对角线.若∠1=∠2,∠A=80°,则∠ADC等于( )
A.60°
B.80°
C.90°
D.100°
7.若AD是△ABC的中线,则下列结论正确的是( )
A.AD⊥BC
B.BD=CD
C.∠BAD=∠CAD
D.AD=BC
8.如图所示,△ABC的边AC上的高是( )
A.线段AE
B.线段BA
C.线段BD
D.线段DA
9.下列图形中,具有稳定性的是( )
A.
B.
C.
D.
10.下列图形中不具有稳定性是( )
A.
B.
C.
D.
11.已知三角形两边长分别为4和8,则该三角形第三边的长可能是( )
A.4
B.5
C.12
D.13
12.在下列长度的三条线段中,能围成三角形的是( )
A.2,3,4
B.2,3,5
C.3,5,9
D.8,4,4
13.如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=45°,∠C=73°,则∠DAE的度数是( )
A.14°
B.24°
C.19°
D.9°
14.已知直线l1∥l2,将一块直角三角板ABC(其中∠A是30°,∠C是60°)按如图所示方式放置,若∠1=84°,则∠2等于( )
A.56°
B.64°
C.66°
D.76°
15.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小(x+40)°,则x的值等于( )
A.15
B.20
C.30
D.40
16.如图,∠A=70°,O是AB上一点,直线OD与AB所夹角∠BOD=83°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转
度.
17.如图,AB∥CD,点M为CD上一点,MF平分∠CME.若∠1=57°,则∠EMD的大小为
度.
18.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为
度.
19.如图,共有
个三角形.
20.如图,在△ABC中,AD是高,点E在DC上,连接AE,则该图中以AD为高的三角形共有
个.
21.盖房子的时候,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条的根据是
.
22.已知△ABC的两条边a、b的长分别为4和7,则第三边c的取值范围是
.
23.如图,AE,AD分别是△ABC的高和角平分线,且∠B=36°,∠C=76°,则∠DAE的度数为
.
24.如图,CE是△ABC外角的平分线,且AB∥CE,若∠ACB=36°,则∠A等于
度.
25.n边形没有对角线,m边形从一个顶点出发最多引5条对角线,则n+m=
.
26.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
27.如图,AO∥CD,OB∥DE,∠O=40°,求∠D的度数.
(1)请完成下列书写过程.
∵AO∥CD(已知)
∴∠O=
=40°(
)
又∵OB∥DE(已知)
∴
=∠1=
°(
)
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=
°.
28.已知:直线GH分别与直线AB,CD交于点E,F.EM平分∠BEF,FN平分∠CFE,并且EM∥FN.
(1)如图1,求证:AB∥CD;
(2)如图2,∠AEF=2∠CFN,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为135°.
29.如图,在三角形ABC中,AB=10cm,AC=6cm,D是BC的中点,E点在边AB上,三角形BDE与四边形ACDE的周长相等.
(1)求线段AE的长.
(2)若图中所有线段长度的和是53cm,求BC+DE的值.
参考答案
1.解:要AD∥BC,只需∠A=∠CBE,
故选:A.
2.解:①∠1=∠2不能判定AB∥CD,不符合题意;
②∵∠1=∠3,∴AB∥CD,符合题意;
③∵∠2=∠4,∴AB∥CD,符合题意;
④∠DAB+∠ABC=180°;不能判定AB∥CD,不符合题意;
⑤∵∠BAD+∠ADC=180°,∴AB∥CD,符合题意.
故选:D.
3.解:过点E作EF∥AB,则EF∥CD,如图所示.
∵EF∥AB,
∴∠BAE=∠AEF.
∵EF∥CD,
∴∠C=∠CEF.
∵AE⊥CE,
∴∠AEC=90°,即∠AEF+∠CEF=90°,
∴∠BAE+∠C=90°.
∵∠1=125°,∠1+∠BAE=180°,
∴∠BAE=180°﹣125°=55°,
∴∠C=90°﹣55°=35°.
故选:A.
4.解:∵AD∥BC,
∴∠3=∠1,
故选:A.
5.解:∵AD⊥BC,FG⊥BC,
∴∠FGD=∠ADB=90°,
∴FG∥AD,
故①正确;
∵DE∥AC,∠BAC=90°,
∴DE⊥AB,
不能证明DE为∠ADB的平分线,
故②错误;
∵AD⊥BC,
∴∠B+∠BAD=90°,
∵DE⊥AB,
∴∠BAD+∠ADE=90°,
∴∠B=∠ADE,
故③正确;
∵∠BAC=90°,DE⊥AB,
∴∠CFG+∠C=90°,∠BDE+∠B=90°,∠C+∠B=90°,
∴∠CFG+∠BDE=90°,
故④正确,
综上所述,正确的选项①③④,
故选:C.
6.解:∵∠1=∠2,
∴AB∥CD,
∴∠A+∠ADC=180°,
∵∠A=80°,
∴∠ADC=180°﹣80°=100°,
故选:D.
7.解:∵AD是△ABC的中线,
∴BD=DC,
故选:B.
8.解:由题意可知,△ABC的边AC上的高是线段BD.
故选:C.
9.解:A、具有稳定性,故此选项符合题意;
B、不具有稳定性,故此选项不符合题意;
C、不具有稳定性,故此选项不符合题意;
D、不具有稳定性,故此选项不符合题意;
故选:A.
10.解:A、具有稳定性,故此选项不合题意;
B、具有稳定性,故此选项不符合题意;
C、具有稳定性,故此选项不合题意;
D、不具有稳定性,故此选项符合题意;
故选:D.
11.解:设第三边的长为x,
∵三角形两边的长分别是4和8,
∴8﹣4<x<8+4,即4<x<12,
只有5有可能,
故选:B.
12.解:根据三角形的三边关系,
A、2+3>4,能组成三角形,符合题意;
B、2+3=5,不能够组成三角形,不符合题意;
C、3+5=8<9,不能组成三角形,不符合题意;
D、4+4=8,不能组成三角形,不符合题意.
故选:A.
13.解:在△ABC中,∠B=45°,∠C=73°,
∴∠BAC=180°﹣∠B﹣∠C=62°.
∵AE平分∠BAC,
∴∠CAE=∠BAC=31°.
∵AD是BC边上的高,
∴AD⊥BC,
∴∠CAD=90°﹣∠C=17°,
∴∠DAE=∠CAE﹣∠CAD=31°﹣17°=14°.
故选:A.
14.解:∵∠3+∠4+∠A=180°,∠A=30°,∠4=∠1=84°,
∴∠3=180°﹣∠A﹣∠4=180°﹣30°﹣84°=66°.
又∵直线l1∥l2,
∴∠2=∠3=66°.
故选:C.
15.解:∵∠C的外角=∠A+∠B,
∴x+40=2x+10+x,
解得x=15.
故选:A.
16.解:∵OD'∥AC,
∴∠BOD'=∠A=70°,
∴∠DOD'=83°﹣70°=13°.
故答案为:13.
17.解:∵AB∥CD,
∴∠CMF=∠1=57°,
∵MF平分∠CME,
∴∠CME=2∠CMF=114°.
又∵∠CME+∠EMD=180°,
∴∠EMD=180°﹣∠CME=180°﹣114°=66°.
故答案为:66.
18.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
19.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
20.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6.
21.解:加上木条后,原不稳定的四边形中具有了稳定的三角形,故这种做法根据的是三角形的稳定性;
故答案为:三角形具有稳定性.
22.解:三角形两边的和>第三边,两边的差<第三边.
则7﹣4<c<7+4,
即3<c<11.
故答案为:3<c<11.
23.解:在△ABC中,∠B=36°,∠C=76°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣36°﹣76°=68°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=×68°=34°.
∵AE是△ABC的高,
∴∠AEC=90°.
在△ACE中,∠AEC=90°,∠C=76°,
∴∠CAE=180°﹣∠AEC﹣∠C=180°﹣90°﹣76°=14°.
∴∠DAE=∠CAD﹣∠CAE=34°﹣14°=20°.
故答案为:20°.
24.解:∵∠ACB=36°,
∴∠ACD=180°﹣∠ACB=180°﹣36°=144°,
∵CE是△ABC外角的平分线,
∴∠ACE=,
∵AB∥CE,
∴∠A=∠ACE=72°,
故答案为:72.
25.解:由题意得:m﹣3=5,n=3,
解得m=8,n=3,
∴m+n=8+3=11.
故答案为:11.
26.证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°,
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF;
(2)∵∠1=∠A,∠4=∠C,
∴∠1+∠A+∠4+∠C=2(∠1+∠4)=180°,
∴∠B+∠D=(180°﹣2∠1)+(180°﹣2∠4)=360°﹣2(∠1+∠4)=180°,
∴AB∥CD.
27.解:(1)∵AO∥CD(已知),
∴∠O=∠1=40°(两直线平行,同位角相等),
又∵OB∥DE(已知),
∴∠D=∠1=40°(两直线平行,同位角相等).
故答案为:∠1,两直线平行,同位角相等,∠D,40°,两直线平行,同位角相等;
(2)若在平面内取一点M,作射线MP∥OA,MQ∥OB,则∠PMQ=(40或140)°.
故答案为:(40或140).
28.(1)证明:∵EM∥FN,
∴∠EFN=∠FEM.
∵EM平分∠BEF,FN平分∠CFE,
∴∠CFE=2∠EFN,∠BEF=2∠FEM.
∴∠CFE=∠BEF.
∴AB∥CD.
(2)∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.理由如下:
∵AB∥CD,
∴∠AEF+∠CFE=180°,
∵FN平分∠CFE,
∴∠CFE=2∠CFN,
∵∠AEF=2∠CFN,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=45°,
∴∠DFN=∠HFN=180°﹣45°=135°,
同理:∠AEM=∠GEM=135°.
∴∠AEM,∠GEM,∠DFN,∠HFN度数都为135°.
29.解:(1)∵三角形BDE与四边形ACDE的周长相等,
∴BD+DE+BE=AC+AE+CD+DE,
∵BD=DC,
∴BE=AE+AC,
设AE=x
cm,则BE=(10﹣x)cm,
由题意得,10﹣x=x+6.
解得,x=2,
∴AE=2cm;
(2)图中共有8条线段,
它们的和为:AE+EB+AB+AC+DE+BD+CD+BC=2AB+AC+2BC+DE,
由题意得,2AB+AC+2BC+DE=53,
∴2BC+DE=53﹣(2AB+AC)=53﹣(2×10+6)=27,
∴BC+DE=(cm).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
