人教版七年级下册数学第五章相交线与平行线5.3平行线的性质
文档属性
| 名称 | 人教版七年级下册数学第五章相交线与平行线5.3平行线的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-21 13:42:04 | ||
图片预览




文档简介
(共24张PPT)
1、知识目标:使学生了解平行线的性质和判定的区别,会运用它们进行简单推理和计算。
2、智能目标:使学生领会数形结合、转化的数学思想方法,提高学生分析问题和解决问题的能力。
3、思想目标:通过实际问题的深入和解决向学生渗透几何知识来源于实践并反作用于实践及认识事物的规律 。
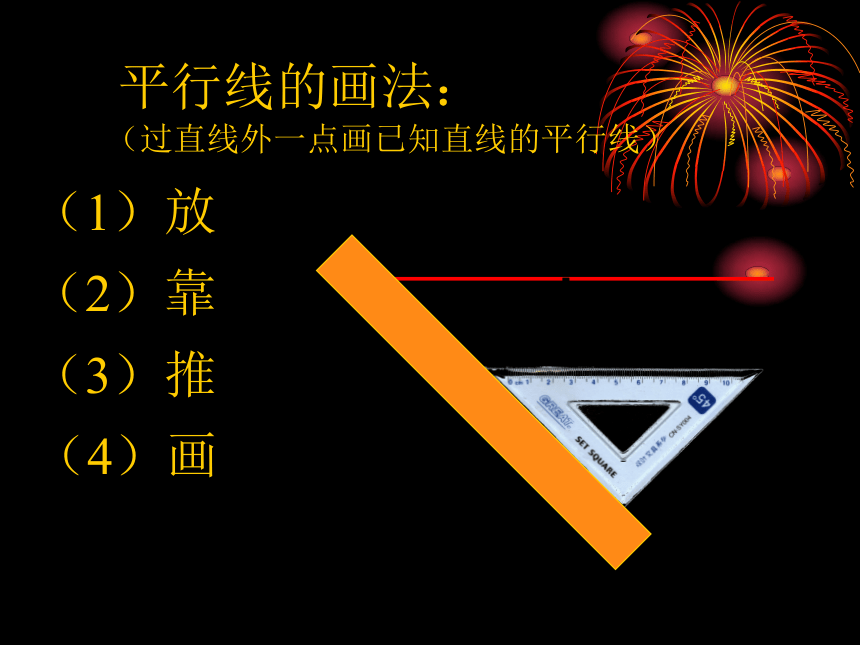
平行线的画法:
(过直线外一点画已知直线的平行线)
(1)放
(2)靠
(3)推
(4)画
·
a
P
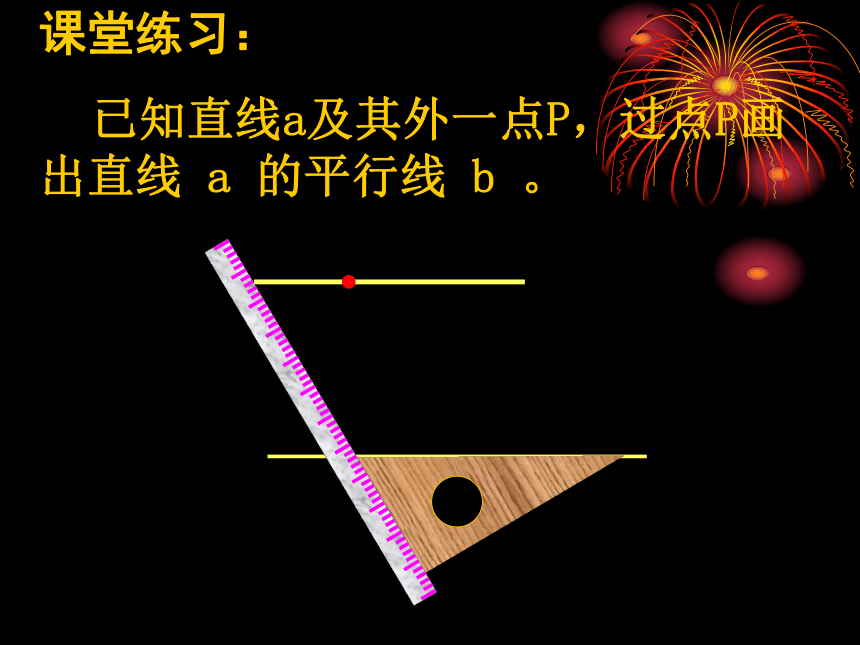
课堂练习:
已知直线a及其外一点P,过点P画出直线 a 的平行线 b 。
b
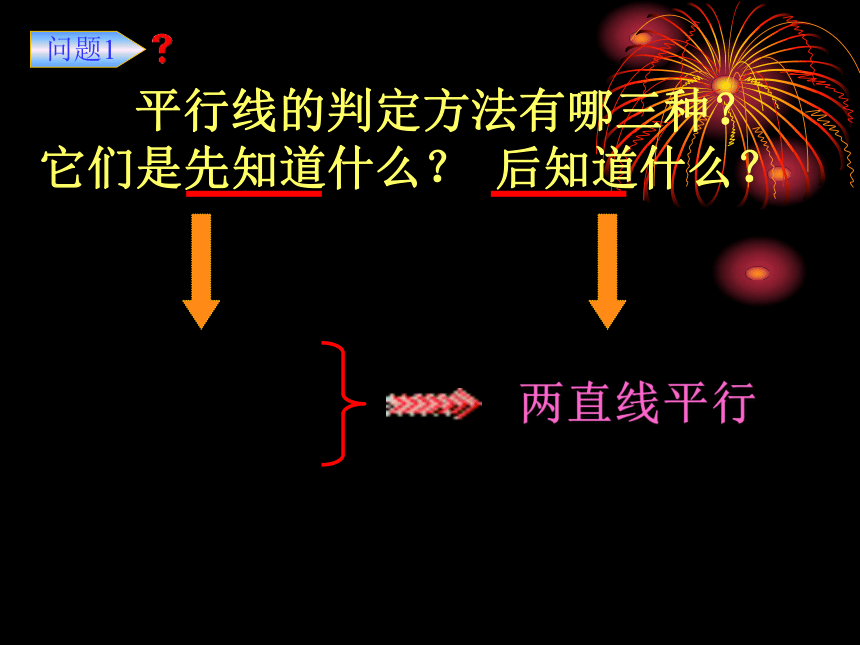
平行线的判定方法有哪三种?
它们是先知道什么? 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
问题1
根据同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行。
问题2
反过来,如果两直线平行,同位角、内错角、同旁内角各有什么关系呢?
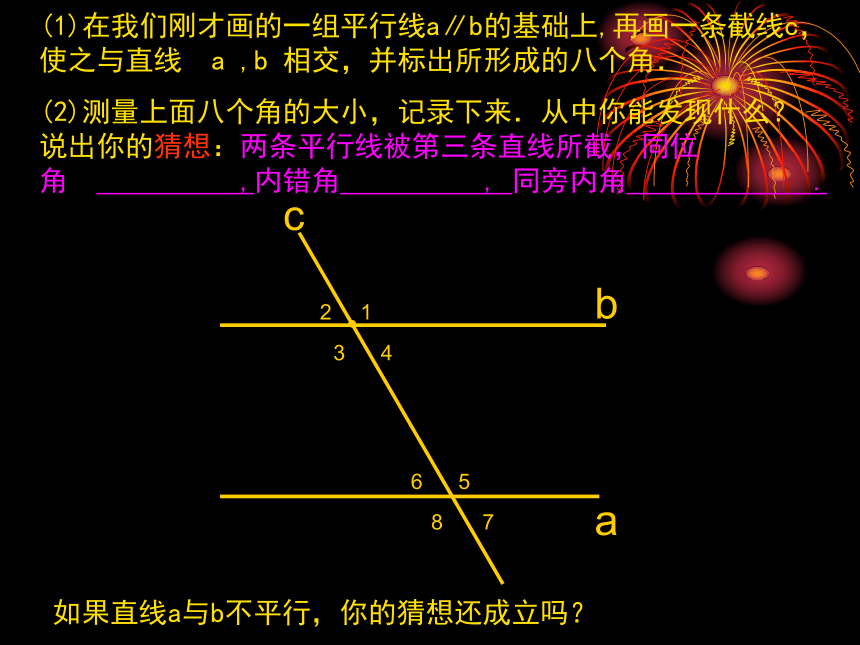
(1)在我们刚才画的一组平行线a∥b的
基础上,再画一条截线c,使之与直线
a ,b 相交,并标出所形成的八个角.
(2)测量上面八个角的大小,记录下
来.从中你能发现什么?
a
1
b
c
1
2
3
4
5
6
8
7
(1)在我们刚才画的一组平行线a∥b的基础上,再画一条截线c, 使之与直线 a ,b 相交,并标出所形成的八个角.
(2)测量上面八个角的大小,记录下来.从中你能发现什么? 说出你的猜想:两条平行线被第三条直线所截,同位角 ,内错角 , 同旁内角 .
如果直线a与b不平行,你的猜想还成立吗?
a
b
c
问题
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
2
1
结论
平行线的性质1(公理):
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 2与 3有什么关系?
平行线的性质2:
两条平行线被第三条直线所截,内错角相等 。
简单说成:两直线平行,内错角相等。
例如:如右图
因为 a∥b,
所以 ∠1= ∠2( )
又因为∠1 = ___(对顶角相等),
所以∠ 2 = ∠3.
两直线平行,同位角相等
∠3
平行线的性质1(公理):两直线平行,同位角相等。
c
2
3
1
b
a
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,
那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
平行线的性质1(公理):两直线平行,同位角相等。
平行线的性质2(公理):两直线平行,内错角相等。
4
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
(1)两直线平行,同位角相等;
简单地说,就是:
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ,你想一想,梯形另外两个角
各是多少度?
解:因为梯形上.下底互相平行,所以
梯形的另外两个 角分别是
A
D
B
C
例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ∠A=115°,∠D=100°,你想一想,梯形另外两个角
各是多少度?
解: ∵ AD∥BC (梯形的定义)
A
D
B
C
∴ ∠A+∠B=180°(两直线平行,同旁内角互补)
∠D+∠C=180°(两直线平行,同旁内角互补)
∴ ∠B=180°-115 °= 65 °
∠C=180°-100 °= 80 °
又∵ ∠A=115° ,∠D=100°(已知)
练习
1.如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠1= 54°(已知)
∴ ∠2=∠1 =54°(对顶角相等)
∵ a∥b(已知)
∴ ∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° -54°=126°
∴ ∠4=∠1=54°(两直线平行,同位角相等)
1
2
3
4
a
b
E
D
C
B
A
(已知)
解:(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证明)
∴∠C= ∠ AED=40 °
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
2.如图,D是AB上一点,E是AC上一点,∠ADE=60 ° ∠B=60 °∠AED=40°
(1)DE和BC平行吗?为什么?
(2) ∠C是多少度,为什么?
如图: 1= 2(已知)
AD// BC
( )
BCD+ D=180
( )
内错角相等,两直线平行
两直线平行,同旁内角互补
2
1
D
C
B
A
如图:已知 1= 2
求证: BCD+ D=180
平行线的“判定”与“性质”有什么不同
比一比
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
课堂小结
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
布置作业:
P22习题5.3
第3、6题。
预习下节课内容。
1、知识目标:使学生了解平行线的性质和判定的区别,会运用它们进行简单推理和计算。
2、智能目标:使学生领会数形结合、转化的数学思想方法,提高学生分析问题和解决问题的能力。
3、思想目标:通过实际问题的深入和解决向学生渗透几何知识来源于实践并反作用于实践及认识事物的规律 。
平行线的画法:
(过直线外一点画已知直线的平行线)
(1)放
(2)靠
(3)推
(4)画
·
a
P
课堂练习:
已知直线a及其外一点P,过点P画出直线 a 的平行线 b 。
b
平行线的判定方法有哪三种?
它们是先知道什么? 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
问题1
根据同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行。
问题2
反过来,如果两直线平行,同位角、内错角、同旁内角各有什么关系呢?
(1)在我们刚才画的一组平行线a∥b的
基础上,再画一条截线c,使之与直线
a ,b 相交,并标出所形成的八个角.
(2)测量上面八个角的大小,记录下
来.从中你能发现什么?
a
1
b
c
1
2
3
4
5
6
8
7
(1)在我们刚才画的一组平行线a∥b的基础上,再画一条截线c, 使之与直线 a ,b 相交,并标出所形成的八个角.
(2)测量上面八个角的大小,记录下来.从中你能发现什么? 说出你的猜想:两条平行线被第三条直线所截,同位角 ,内错角 , 同旁内角 .
如果直线a与b不平行,你的猜想还成立吗?
a
b
c
问题
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
2
1
结论
平行线的性质1(公理):
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
1
2
3
a
b
思考
回答
如图,已知:a// b
那么 2与 3有什么关系?
平行线的性质2:
两条平行线被第三条直线所截,内错角相等 。
简单说成:两直线平行,内错角相等。
例如:如右图
因为 a∥b,
所以 ∠1= ∠2( )
又因为∠1 = ___(对顶角相等),
所以∠ 2 = ∠3.
两直线平行,同位角相等
∠3
平行线的性质1(公理):两直线平行,同位角相等。
c
2
3
1
b
a
解: a//b (已知)
1= 2(两直线平行,同位角相等)
1+ 3=180°(邻补角定义)
2+ 3=180°(等量代换)
如图:已知a//b,
那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
平行线的性质1(公理):两直线平行,同位角相等。
平行线的性质2(公理):两直线平行,内错角相等。
4
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
(1)两直线平行,同位角相等;
简单地说,就是:
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ,你想一想,梯形另外两个角
各是多少度?
解:因为梯形上.下底互相平行,所以
梯形的另外两个 角分别是
A
D
B
C
例1 小青不小心把家里的梯形玻璃块打碎了,还剩下梯
形上底的一部分(如图)。要订造一块新的玻璃,已经
量得 ∠A=115°,∠D=100°,你想一想,梯形另外两个角
各是多少度?
解: ∵ AD∥BC (梯形的定义)
A
D
B
C
∴ ∠A+∠B=180°(两直线平行,同旁内角互补)
∠D+∠C=180°(两直线平行,同旁内角互补)
∴ ∠B=180°-115 °= 65 °
∠C=180°-100 °= 80 °
又∵ ∠A=115° ,∠D=100°(已知)
练习
1.如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠1= 54°(已知)
∴ ∠2=∠1 =54°(对顶角相等)
∵ a∥b(已知)
∴ ∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° -54°=126°
∴ ∠4=∠1=54°(两直线平行,同位角相等)
1
2
3
4
a
b
E
D
C
B
A
(已知)
解:(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证明)
∴∠C= ∠ AED=40 °
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
2.如图,D是AB上一点,E是AC上一点,∠ADE=60 ° ∠B=60 °∠AED=40°
(1)DE和BC平行吗?为什么?
(2) ∠C是多少度,为什么?
如图: 1= 2(已知)
AD// BC
( )
BCD+ D=180
( )
内错角相等,两直线平行
两直线平行,同旁内角互补
2
1
D
C
B
A
如图:已知 1= 2
求证: BCD+ D=180
平行线的“判定”与“性质”有什么不同
比一比
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
图形
已知
结果
结论
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
课堂小结
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
布置作业:
P22习题5.3
第3、6题。
预习下节课内容。
