苏科版 八年级下 9.2 反比例函数的图象与性质 课件1
文档属性
| 名称 | 苏科版 八年级下 9.2 反比例函数的图象与性质 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-21 14:31:02 | ||
图片预览








文档简介
(共22张PPT)
初中数学八年级下册
(苏科版)
9.2 反比例函数的图象与性质
请画出下列6个反比例函数的图象:
请大家进行分类并说明分类的依据,探索图象的特征.
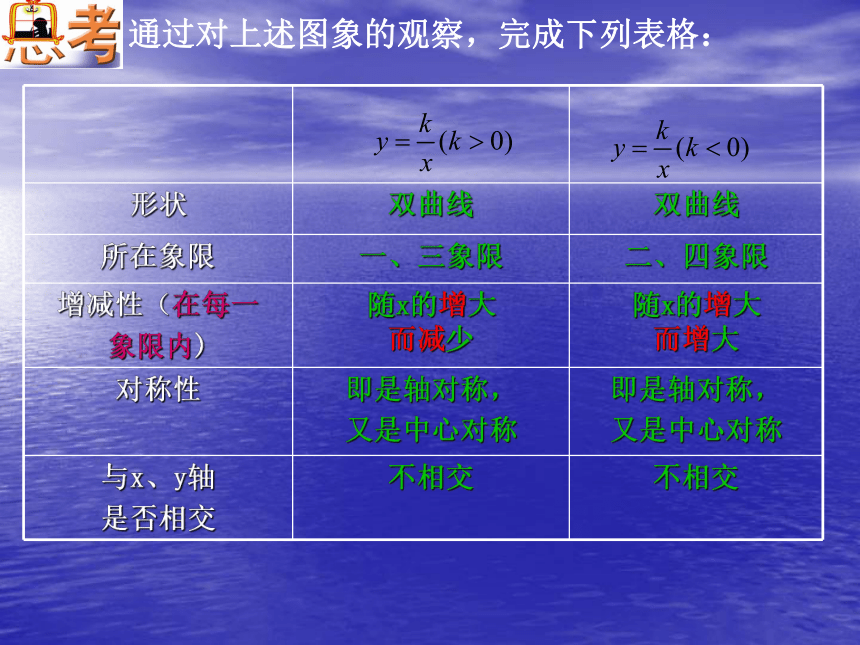
形状 双曲线 双曲线
所在象限 一、三象限 二、四象限
增减性(在每一
象限内) 随x的增大
而减少 随x的增大
而增大
对称性 即是轴对称,
又是中心对称 即是轴对称,
又是中心对称
与x、y轴
是否相交 不相交 不相交
通过对上述图象的观察,完成下列表格:
反比例函数y= (k为常数,k≠0)的图象是双曲线.
当k>0时,双曲线的两支分别在第一、三象限,在每一个象限内,y随x的增大而减小;
当k<0时,双曲线的两支分别在第二、四象限,在每一个象限内,y随x的增大而增大.
如果将反比例函数的图象绕原点旋转180度,你有什么发现?
画出函数图象上的点A(4,-2),找出点A关于原点O的对称点A’,点A’在这个图象上吗?
画出函数图象上的任意一点B,找出点B关于原点O的对称点B’,点B’在这个图象上吗?
将反比例函数的图象绕原点旋转后,能与原来的图象重合,因此反比例函数图象是中心对称图形,它的对称中心是坐标系的原点.
例1.已知反比例函数y= 的图象经过
A(2,—4).
(1)k的值;
(2)这个函数的图象在哪几个象限?y随x的 增大怎样变化?
(3)画出函数的图象;
(4)点B( ,—16)、C(—3,5)在这
个函数的图象上吗?
例2.已知反比例函数y= 的图象上有两点
P(1,a), Q(b,2.5).
(1) 求a、b的值;
(2) 过点P作y轴的垂线交于点M,求△PMO的面积;
(3) 过点Q作x轴的垂线交于点N,求△QNO的面积;
(4)过双曲线上任意一点A(m,n)作x轴(或y轴)
的垂线,垂足为B,求△ABO的面积;
(5)你发现了什么规律?
1、反比例函数①y= ;②y= ;③7y=-
;④y= 的图象中:
(1)在第一、三象限的是 ,在第二、四 象限的是 .
(2)在其所在的每一个象限内,y随x的增大而增 大的是 .
2.已知反比例函数的图象经过点A(-6,-3)
(1)写出函数关系式.
(2)这个函数的图象在哪几个象限?y随x的增大 怎样变化?
(3)点B(4,),C(2,—5)在这个函数的图象上吗
1.若反比例函数y= 的图象经过第二、四
象限,求函数的解析式.
2.函数y= 与y=ax的图象的一个交点A的坐标
是(-1,-3),
(1)求这两个函数的解析式;
(2)在同一直角坐标系内,画出它们的图象;
(3)你能求出这两个图象的另一个交点B的坐标吗?怎样求?
正比例函数y=kx 反比例函数
k>0 k<0 k>0 k<0
图象所在象限
增减性
1.填表
2.老师给出一个函数,甲、乙各指出这
个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,y随x的增大而
减小.
请你写出一个满足上述性质的函数关系式
.
3.点(-2,y1)(-1,y2)(1,y3)在反比例函数 的图象上,比较y1、y2、y3的大小.
思考:比较y1、y2、y3的大小有哪些方法?
代人法、图象法、增减性法
例1:如图,是反比例函数 的图象的一支.
函数图象的另一支在第几象限?
求常数m的取值范围.
(3)点A(-3,y1)、B(-1,y2)、C(2,y3)都在这个反比例函数的图象上,比较y1、y2和y3的大小.
分析: 由于反比例函数图象的一支在第一象限,所以另一支在第三象限,显然2-m﹥0,由此得到m的取值范围,由于反比例函数的自变量x的取值范围是x≠0,所以其图象是分段的,不连续的,在讨论函数值的大小问题时,我们必须分象限来进行讨论.问题3的解决有如下几种方法:代人法,即代人到解析式中求解后进行比较;图象法,利用图象观察、比较得出;增减性法,利用反比例函数图象的增减性在每个分支上进行分析、解决.
1.对于反比例函数y = x(k)(k>0),当x1 < 0< x22.已知反比例函数 的图象具有以下特征:在同一象限内,y随x增大而增大,
(1)求n的取值范围.
(2)点(2,a)、(-1,b)、(-2,c)都在这个反比例函数图象上,比较a、b、c的大小.
3.已知反比例函数 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1) 求k、n的值;
(2) 求一次函数y=mx+b的解析式.
(3) 求△POQ的面积.
4. 已知反比例函数y1 = 和一次函数 y2=kx+2的图象都过点P(a,2a).
(1) 求a与k的值;
(2) 在同一坐标系中画出这两个函数的图象;
(3) 若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1﹥y2
初中数学八年级下册
(苏科版)
9.2 反比例函数的图象与性质
请画出下列6个反比例函数的图象:
请大家进行分类并说明分类的依据,探索图象的特征.
形状 双曲线 双曲线
所在象限 一、三象限 二、四象限
增减性(在每一
象限内) 随x的增大
而减少 随x的增大
而增大
对称性 即是轴对称,
又是中心对称 即是轴对称,
又是中心对称
与x、y轴
是否相交 不相交 不相交
通过对上述图象的观察,完成下列表格:
反比例函数y= (k为常数,k≠0)的图象是双曲线.
当k>0时,双曲线的两支分别在第一、三象限,在每一个象限内,y随x的增大而减小;
当k<0时,双曲线的两支分别在第二、四象限,在每一个象限内,y随x的增大而增大.
如果将反比例函数的图象绕原点旋转180度,你有什么发现?
画出函数图象上的点A(4,-2),找出点A关于原点O的对称点A’,点A’在这个图象上吗?
画出函数图象上的任意一点B,找出点B关于原点O的对称点B’,点B’在这个图象上吗?
将反比例函数的图象绕原点旋转后,能与原来的图象重合,因此反比例函数图象是中心对称图形,它的对称中心是坐标系的原点.
例1.已知反比例函数y= 的图象经过
A(2,—4).
(1)k的值;
(2)这个函数的图象在哪几个象限?y随x的 增大怎样变化?
(3)画出函数的图象;
(4)点B( ,—16)、C(—3,5)在这
个函数的图象上吗?
例2.已知反比例函数y= 的图象上有两点
P(1,a), Q(b,2.5).
(1) 求a、b的值;
(2) 过点P作y轴的垂线交于点M,求△PMO的面积;
(3) 过点Q作x轴的垂线交于点N,求△QNO的面积;
(4)过双曲线上任意一点A(m,n)作x轴(或y轴)
的垂线,垂足为B,求△ABO的面积;
(5)你发现了什么规律?
1、反比例函数①y= ;②y= ;③7y=-
;④y= 的图象中:
(1)在第一、三象限的是 ,在第二、四 象限的是 .
(2)在其所在的每一个象限内,y随x的增大而增 大的是 .
2.已知反比例函数的图象经过点A(-6,-3)
(1)写出函数关系式.
(2)这个函数的图象在哪几个象限?y随x的增大 怎样变化?
(3)点B(4,),C(2,—5)在这个函数的图象上吗
1.若反比例函数y= 的图象经过第二、四
象限,求函数的解析式.
2.函数y= 与y=ax的图象的一个交点A的坐标
是(-1,-3),
(1)求这两个函数的解析式;
(2)在同一直角坐标系内,画出它们的图象;
(3)你能求出这两个图象的另一个交点B的坐标吗?怎样求?
正比例函数y=kx 反比例函数
k>0 k<0 k>0 k<0
图象所在象限
增减性
1.填表
2.老师给出一个函数,甲、乙各指出这
个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,y随x的增大而
减小.
请你写出一个满足上述性质的函数关系式
.
3.点(-2,y1)(-1,y2)(1,y3)在反比例函数 的图象上,比较y1、y2、y3的大小.
思考:比较y1、y2、y3的大小有哪些方法?
代人法、图象法、增减性法
例1:如图,是反比例函数 的图象的一支.
函数图象的另一支在第几象限?
求常数m的取值范围.
(3)点A(-3,y1)、B(-1,y2)、C(2,y3)都在这个反比例函数的图象上,比较y1、y2和y3的大小.
分析: 由于反比例函数图象的一支在第一象限,所以另一支在第三象限,显然2-m﹥0,由此得到m的取值范围,由于反比例函数的自变量x的取值范围是x≠0,所以其图象是分段的,不连续的,在讨论函数值的大小问题时,我们必须分象限来进行讨论.问题3的解决有如下几种方法:代人法,即代人到解析式中求解后进行比较;图象法,利用图象观察、比较得出;增减性法,利用反比例函数图象的增减性在每个分支上进行分析、解决.
1.对于反比例函数y = x(k)(k>0),当x1 < 0< x2
(1)求n的取值范围.
(2)点(2,a)、(-1,b)、(-2,c)都在这个反比例函数图象上,比较a、b、c的大小.
3.已知反比例函数 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
(1) 求k、n的值;
(2) 求一次函数y=mx+b的解析式.
(3) 求△POQ的面积.
4. 已知反比例函数y1 = 和一次函数 y2=kx+2的图象都过点P(a,2a).
(1) 求a与k的值;
(2) 在同一坐标系中画出这两个函数的图象;
(3) 若两函数图象的另一个交点是Q(0.5,4),利用图象指出:当x为何值时,有y1﹥y2
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
