苏科版八年级下 9.2 反比例函数的图象与性质 课件2
文档属性
| 名称 | 苏科版八年级下 9.2 反比例函数的图象与性质 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-21 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
2.反比例函数的图象与性质
复习回顾
1.反比例函数y=k/x(k≠0)的图象是一个怎样的图象?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线
2.反比例函数的图象的位置与k有怎样关系?
3 反比例函数的图象可能与x轴相交吗?
可能与y轴相交吗?为什么?
不能与x轴、y轴相交。
因为x≠0,所以不与y轴相交;因为y ≠0,所以不与x轴相交。
结论:图像的两个分支无限接近x轴和y轴,但永远不会与X轴、y轴相交。
4、 将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?
能重合,双曲线是中心对称图形,
对称中心是原点。
能重合,双曲线是轴对称图形,有两条对称轴,是直线y=x和直线y=-x
5、 将反比例函数的图象沿着直线y=x或直线y=-x折叠后,两部分图象能重合吗?
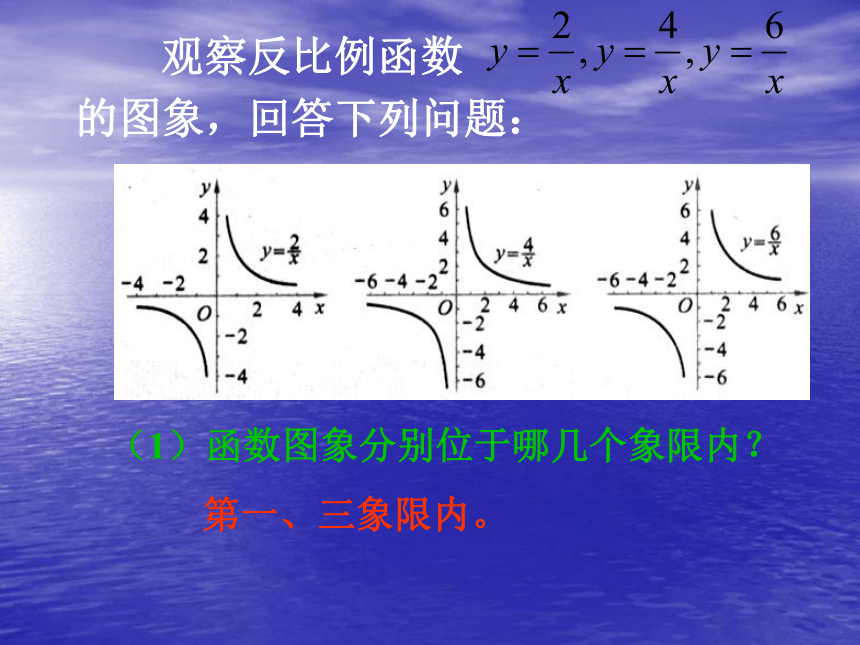
(1)函数图象分别位于哪几个象限内?
第一、三象限内。
观察反比例函数 的图象,回答下列问题:
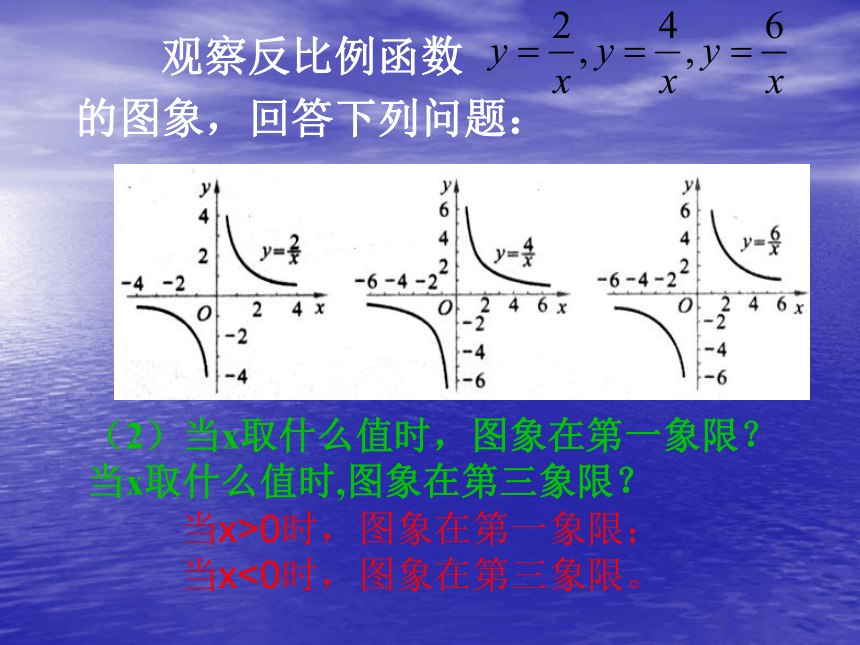
观察反比例函数 的图象,回答下列问题:
(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
当x>0时,图象在第一象限;
当x<0时,图象在第三象限。
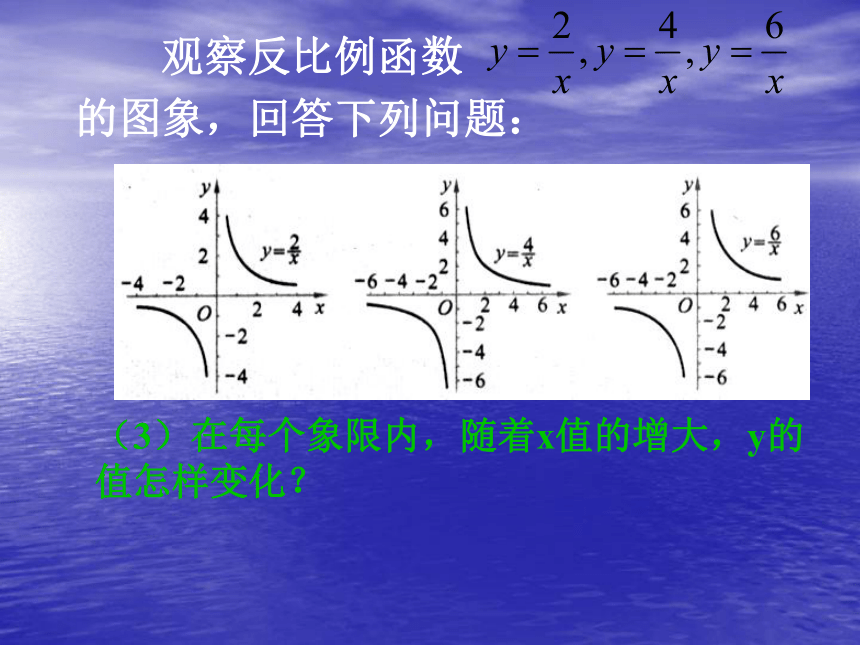
(3)在每个象限内,随着x值的增大,y的值怎样变化?
观察反比例函数 的图象,回答下列问题:
A(x1,y1)
B(x2,y2)
y2
x1
x2
y1
0
在每一象限内,y的值随x值的增大而减小。
(3)在每个象限内,随着x值的增大,y的值怎样变化?
观察反比例函数 的图象,回答下列问题:
如果k=-2, -4,-6,那么函数
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内?
x>0时,图象在第四象限;
x<0 时,图象在第二象限。
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一象限内,y的值随x值的增大而增大
如果k=-2, -4,-6,那么函数
的图象有又什么共同特征?
反比例函数的性质
反比例函数 y=k/x(k≠0)
K的符号 k >0 k<0
图象
性质 ① x的取值范围x ≠0,
Y的取值范围y ≠0
②当k >0时,函数图象的两个分支分别在第一、第三象限,在每个象限内,y随x的增大而减小 ①x的取值范围是x ≠0,
Y的取值范围y ≠0
②当k <0时,函数图象的两个分支分别在第二、第四象限,在每个象限内,y随x的增大而增大
x
y
0
x
y
0
习题5.3
1.下列函数中,其图象位于第一、三象限的有 __________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的图象上,比较y1、 y2 、y3的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x10, ∴点A(-2,y1),点B(-1,y2)在第三象限点C(3,y3)在第一象限。
∴y3>0, y2(1)(2)(3)
(4)
你能解答第(2)小题了吗
(2)、如果点A(-2,y1),B(-1, y2)和C(3,y3)都在反比例函数 y=k/x 的图像上,那么y1,y2与y3的大小关系又如何呢?
当k>0时, y2 < y1 < 0 < y3
当k<0时, y3 < 0 < y1 < y2
想一想
在一个反比例函数图象上任取两点P,Q,
过点P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为s1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为s2。s1与s2有什么关系?为什么?
P
Q
S1
S2
R
S3
S1、S2有什么关系?为什么?
M
N
R
(x,y)
因为:RM=|Y|,RN= |X|所以S距=|X||Y|= |XY|=| K|
结论:在反比例函数 y=k/x(k ≠0) 的图像上任取一点,过这点作x轴,y轴的平行线,与坐标轴围成的矩形面积总等于|k|.
因为:RM=|Y|,RN= |X|所以S距=|X||Y|=|XY|=|K|
2.反比例函数的图象与性质
复习回顾
1.反比例函数y=k/x(k≠0)的图象是一个怎样的图象?
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
反比例函数的图象是双曲线
2.反比例函数的图象的位置与k有怎样关系?
3 反比例函数的图象可能与x轴相交吗?
可能与y轴相交吗?为什么?
不能与x轴、y轴相交。
因为x≠0,所以不与y轴相交;因为y ≠0,所以不与x轴相交。
结论:图像的两个分支无限接近x轴和y轴,但永远不会与X轴、y轴相交。
4、 将反比例函数的图象绕原点旋转180°后,能与原来的图象重合吗?
能重合,双曲线是中心对称图形,
对称中心是原点。
能重合,双曲线是轴对称图形,有两条对称轴,是直线y=x和直线y=-x
5、 将反比例函数的图象沿着直线y=x或直线y=-x折叠后,两部分图象能重合吗?
(1)函数图象分别位于哪几个象限内?
第一、三象限内。
观察反比例函数 的图象,回答下列问题:
观察反比例函数 的图象,回答下列问题:
(2)当x取什么值时,图象在第一象限?当x取什么值时,图象在第三象限?
当x>0时,图象在第一象限;
当x<0时,图象在第三象限。
(3)在每个象限内,随着x值的增大,y的值怎样变化?
观察反比例函数 的图象,回答下列问题:
A(x1,y1)
B(x2,y2)
y2
x1
x2
y1
0
在每一象限内,y的值随x值的增大而减小。
(3)在每个象限内,随着x值的增大,y的值怎样变化?
观察反比例函数 的图象,回答下列问题:
如果k=-2, -4,-6,那么函数
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内?
x>0时,图象在第四象限;
x<0 时,图象在第二象限。
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一象限内,y的值随x值的增大而增大
如果k=-2, -4,-6,那么函数
的图象有又什么共同特征?
反比例函数的性质
反比例函数 y=k/x(k≠0)
K的符号 k >0 k<0
图象
性质 ① x的取值范围x ≠0,
Y的取值范围y ≠0
②当k >0时,函数图象的两个分支分别在第一、第三象限,在每个象限内,y随x的增大而减小 ①x的取值范围是x ≠0,
Y的取值范围y ≠0
②当k <0时,函数图象的两个分支分别在第二、第四象限,在每个象限内,y随x的增大而增大
x
y
0
x
y
0
习题5.3
1.下列函数中,其图象位于第一、三象限的有 __________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1)已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的图象上,比较y1、 y2 、y3的大小关系。
解:∵k=4>0
∴图象在第一、三象限内,每一象限内y随x的增大而减小
∵x1
∴y3>0, y2
(4)
你能解答第(2)小题了吗
(2)、如果点A(-2,y1),B(-1, y2)和C(3,y3)都在反比例函数 y=k/x 的图像上,那么y1,y2与y3的大小关系又如何呢?
当k>0时, y2 < y1 < 0 < y3
当k<0时, y3 < 0 < y1 < y2
想一想
在一个反比例函数图象上任取两点P,Q,
过点P分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为s1;过点Q分别作x轴、y轴的平行线,与坐标轴围成的矩形面积为s2。s1与s2有什么关系?为什么?
P
Q
S1
S2
R
S3
S1、S2有什么关系?为什么?
M
N
R
(x,y)
因为:RM=|Y|,RN= |X|所以S距=|X||Y|= |XY|=| K|
结论:在反比例函数 y=k/x(k ≠0) 的图像上任取一点,过这点作x轴,y轴的平行线,与坐标轴围成的矩形面积总等于|k|.
因为:RM=|Y|,RN= |X|所以S距=|X||Y|=|XY|=|K|
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
