2011——2012学年度第二学期寒假学情检测数学试卷
文档属性
| 名称 | 2011——2012学年度第二学期寒假学情检测数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 123.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-21 15:04:55 | ||
图片预览




文档简介
2011——2012学年度第二学期寒假学情检测数学试卷
(时间120分钟 分值150分)
一、选择题(每题4分,共40分)
1、在平面直角坐标系中,抛物线与轴的交点的个数是( )
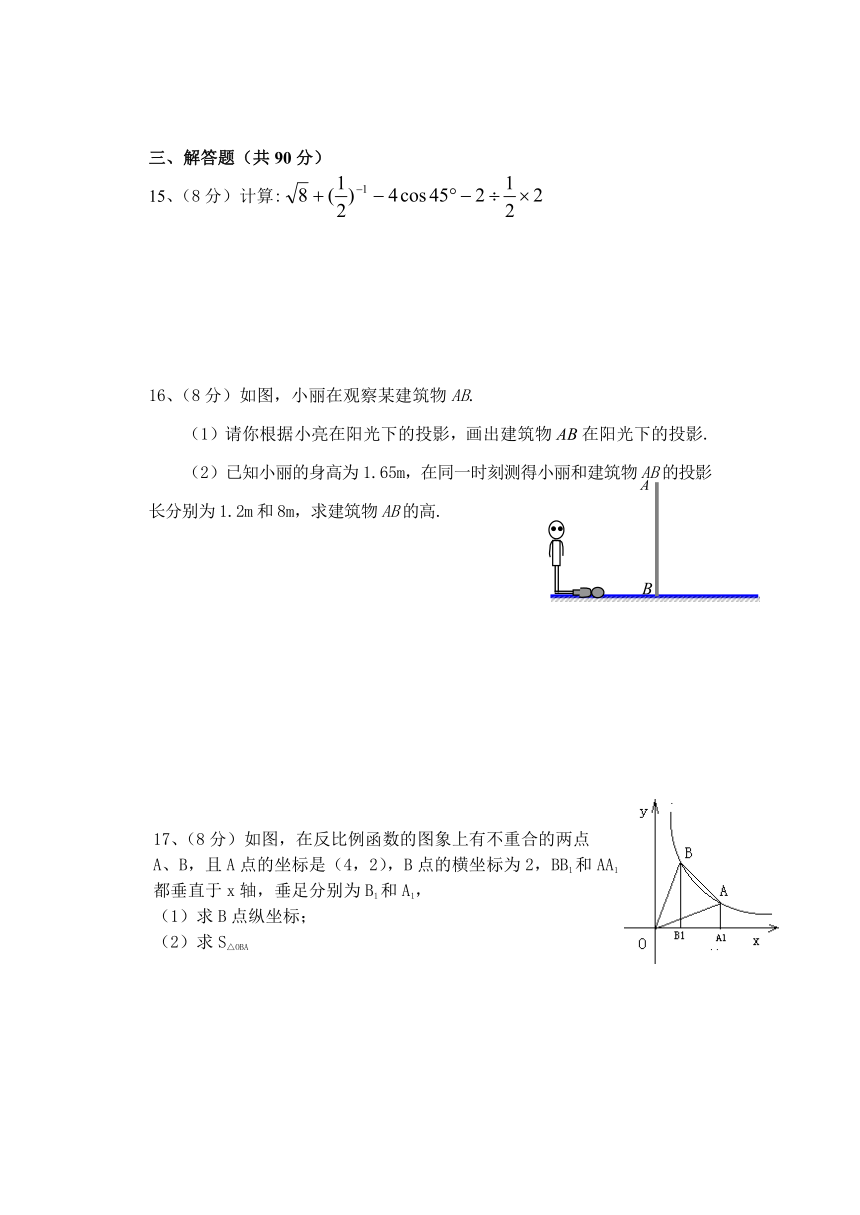
A.3 B.2 C.1 D.0
2、如图,在△ABC中,已知∠C=90°,BC=5,AC=12,
则它的内切圆周长是( )
A. B. C.2 D.
3、如果点O为△ABC的外心,∠BOC=70°,那么∠BAC等于( )
A.35° B.110° C.145° D. 35°或145°
4、如图3,从圆外一点引圆的两条切线,切点分别为.如果,,那么点间的距离是( )
A.16 B. C. D.
5、如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
S=2 B.S=2.4 C.S=4 D.S与BE长度有关
6、若一圆锥形烟囱帽的侧面积是2000лcm2,母线长为50cm,则这个烟囱帽的底面直径为( ).
A、80cm B、1OOcrn C、 40crn D、60crn
7、比较,,的大小关系是( )
A. B.
C. D.
8、抛物线y=-x2-1的图象大致是( )
9、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
①②③④. (B)④①③②. (C)④②③①. (D)④③②①.
10、已知的三边长分别为,,2,的两边长分别是1和,如果∽相似,那么的第三边长应是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
11、抛物线y=x2+x-4与顶点坐标为
12、宋朝时,中国象棋就已经风靡于全国,中国象棋规定马步为:“ 、 ”形的对角线(即一次对角线为一步),现定义:在棋盘上从点A到点B,马走的最少步称为A与B的“马步距离”, 记作。在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在,,,中最小步的是 ,最小是 步。
13、如图5,平行四边形中,是边上的点,交于点,如果,那么 .
14、如图,一条公路的转弯处是一段圆弧(图中的AB弧),
点O是这段弧的圆心,AB=120m,C是AB弧是一点,OC⊥AB
于D,CD=20m,则该弯路的半径为 .
三、解答题(共90分)
15、(8分)计算:
16、(8分)如图,小丽在观察某建筑物AB.
(1)请你根据小亮在阳光下的投影,画出建筑物在阳光下的投影.
(2)已知小丽的身高为1.65m,在同一时刻测得小丽和建筑物AB的投影长分别为1.2m和8m,求建筑物AB的高.
17、(8分)如图,在反比例函数的图象上有不重合的两点
A、B,且A点的坐标是(4,2),B点的横坐标为2,BB1和AA1
都垂直于x轴,垂足分别为B1和A1,
(1)求B点纵坐标;
(2)求S△OBA
18.(10分)如图2—9, 在 ABCD中,对角线AC,BD交于O点(BD>AC),E、F是BD上的两点.
(1) 当点E、F满足条件: 时,四边形AECF是平行四边形(不必证明);
(2)若四边形AECF是矩形,那么点E、F的位置应满足什么条件 并给出证明.
19、(10分)如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67°,半径OC所在的直线与放置平面垂直,垂足为点E. CE=10.3cm,AD=14cm.求半径OA的长. (精确到0.1cm)
(参考数据:sin67°≈0.92, cos67°≈0.39, tan67°≈2.36)
20、(10分)如图,AB是⊙O的直径,且AB=10,直线CD交⊙O于C、D两点,交AB于E,OP⊥CD于P,∠PEO=45° OP=.
求线段CD的长;
(2)试问将直线CD通过怎样的变换才能与⊙O切于B或A.
21、(10分)东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) 50 51 52 53 ……
销售量p(件) 500 490 480 470 ……
(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连结各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入件为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
22、(12分)九(2)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是____________ m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为m,长方形框架ABCD的面积为S= ________(用含的代数式表示);当AB=_________m时, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为m, 设AB为m,当AB=________m时, 长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.
探索: 如图案(4), 如果铝合金材料总长度为m共有n条竖档时, 那么当竖档AB多少时,长方形框架ABCD的面积最大.
23、(14分)如图①②,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米).
答案:一、
1 2 3 4 5 6 7 8 9 10
D B D B C A B B B A
二、填空
11、12、 ,2 13、 14、100
三、15、解:原式
16、解:(1)如图.
(2)如图,因为DE,AF都垂直于地面,且光线DF∥AC,所以Rt△DEF∽Rt△ABC.所以.所以.所以AB=11(m).即建筑物AB的高为.
17、
18、(1)BE=DF或OE=OF,
(2)OE=OF=OA或OE=OF=OC或OE=OF且AC=EF,
略证:因为OA=OE=OF=OC则,EF=AC 所以四边形A ECF是矩形
解:设OA=xcm, 则OD=(14+x)cm, OE=(10.3+x)cm………………1分
在Rt△ODE中,∠ODE=67°.
∵sin∠ODE= ∴=0.92 …………5分
∴x=32.25
OA≈32.3(cm). …………………………7分
答:半径OA的长约为32.3cm. ………………… 8分
19、解:(1)如图1,连结OC,∵OP⊥CD
∴CP=CD= ,∴CD=2…………… 6分
(2)∵∠PEO=45°,OE=2,BE=3,
∴将直线CD绕着点E逆时针旋转45°后,若再沿射线EB平移3个单位,直线CD与⊙O相切于B,或再沿射线EA平移7个单位,直线CD与⊙O相切于A (如图2) …………… 12分
解:(1)p与x成一次函数关系。 设函数关系式为p=kx+b ,则 解得:k=-10,b=1000 , ∴ p=-10x+1000 经检验可知:当x=52,
p=480,当x=53,p=470时也适合这一关系式
∴所求的函数关系为p=-10x+1000
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000)
∴ y=-10x2+1400x-40000
(3)由y=-10x2+1400x-40000 可知,当时,y有最大值
∴ 卖出价格为70元时,能花得最大利润。
解:(1), (2)-x2+2x ,1, ,
(3)设AB长为m,那么AD为,
S=·=-,
当=时,S最大.
22、
(1)连结OC,∵EF切⊙O于点C,∴OC⊥EF,∴∠1+∠4 =90°
∵AD⊥EF, ∴在Rt△ACD中,∠3+∠4=90°
又 ∵OA=OC, ∴∠1=∠2, ∴∠2 =∠3 即∠DAC=∠BAC
(2)∠BAG=∠DAC,理由如下:
连结BC,∵AB为⊙O的直径,∴∠BCA=90°,∠B+∠BAC=90°
在Rt△AGD中,∠AGD+∠GAD=90°,
又 ∵∠B=∠AGD. ∴∠BAC=∠GAD,
即 ∠BAG+∠GAC=∠GAC+∠DAC,
∴∠BAG=∠DAC
23、【解】过M作AC平行的直线,与OA,FC分别相交于H,N.(1)在Rt△OHM中,∠OHM=90°,OM=5,HM=OM×sinα=3,所以OH=4,MB=HA=5-4=1(单位),1×5=5(cm),所以铁环钩离地面的高度为5cm.
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH=α,所以=sinα=,即得FN=FM,在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=11-3=8(单位),由勾股定理FM2=FN2+MN2,即FM2=(FM)2+82,解得FM=10(单位),10×5=50(cm),所以铁环钩的长度FM为50cm.
考号 姓名 班级
………………………………装………………………………………订……………………………………线………………………………
P
B
A
O
图3
E
D
A
C
B
E
C
D
A
F
B
图5
A
B
p(件)
500
490
480
470
50 51 52 53 x(元/件)
A
B
M
O
F
C
②
①
H
N
A
B
F
C
D
E
(时间120分钟 分值150分)
一、选择题(每题4分,共40分)
1、在平面直角坐标系中,抛物线与轴的交点的个数是( )
A.3 B.2 C.1 D.0
2、如图,在△ABC中,已知∠C=90°,BC=5,AC=12,
则它的内切圆周长是( )
A. B. C.2 D.
3、如果点O为△ABC的外心,∠BOC=70°,那么∠BAC等于( )
A.35° B.110° C.145° D. 35°或145°
4、如图3,从圆外一点引圆的两条切线,切点分别为.如果,,那么点间的距离是( )
A.16 B. C. D.
5、如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则 ( )
S=2 B.S=2.4 C.S=4 D.S与BE长度有关
6、若一圆锥形烟囱帽的侧面积是2000лcm2,母线长为50cm,则这个烟囱帽的底面直径为( ).
A、80cm B、1OOcrn C、 40crn D、60crn
7、比较,,的大小关系是( )
A. B.
C. D.
8、抛物线y=-x2-1的图象大致是( )
9、如图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是 ( )
①②③④. (B)④①③②. (C)④②③①. (D)④③②①.
10、已知的三边长分别为,,2,的两边长分别是1和,如果∽相似,那么的第三边长应是( )
A. B. C. D.
二、填空题(每小题5分,共20分)
11、抛物线y=x2+x-4与顶点坐标为
12、宋朝时,中国象棋就已经风靡于全国,中国象棋规定马步为:“ 、 ”形的对角线(即一次对角线为一步),现定义:在棋盘上从点A到点B,马走的最少步称为A与B的“马步距离”, 记作。在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在,,,中最小步的是 ,最小是 步。
13、如图5,平行四边形中,是边上的点,交于点,如果,那么 .
14、如图,一条公路的转弯处是一段圆弧(图中的AB弧),
点O是这段弧的圆心,AB=120m,C是AB弧是一点,OC⊥AB
于D,CD=20m,则该弯路的半径为 .
三、解答题(共90分)
15、(8分)计算:
16、(8分)如图,小丽在观察某建筑物AB.
(1)请你根据小亮在阳光下的投影,画出建筑物在阳光下的投影.
(2)已知小丽的身高为1.65m,在同一时刻测得小丽和建筑物AB的投影长分别为1.2m和8m,求建筑物AB的高.
17、(8分)如图,在反比例函数的图象上有不重合的两点
A、B,且A点的坐标是(4,2),B点的横坐标为2,BB1和AA1
都垂直于x轴,垂足分别为B1和A1,
(1)求B点纵坐标;
(2)求S△OBA
18.(10分)如图2—9, 在 ABCD中,对角线AC,BD交于O点(BD>AC),E、F是BD上的两点.
(1) 当点E、F满足条件: 时,四边形AECF是平行四边形(不必证明);
(2)若四边形AECF是矩形,那么点E、F的位置应满足什么条件 并给出证明.
19、(10分)如图,点A、B为地球仪的南、北极点,直线AB与放置地球仪的平面交于点D,所成的角度约为67°,半径OC所在的直线与放置平面垂直,垂足为点E. CE=10.3cm,AD=14cm.求半径OA的长. (精确到0.1cm)
(参考数据:sin67°≈0.92, cos67°≈0.39, tan67°≈2.36)
20、(10分)如图,AB是⊙O的直径,且AB=10,直线CD交⊙O于C、D两点,交AB于E,OP⊥CD于P,∠PEO=45° OP=.
求线段CD的长;
(2)试问将直线CD通过怎样的变换才能与⊙O切于B或A.
21、(10分)东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表:
卖出价格x(元/件) 50 51 52 53 ……
销售量p(件) 500 490 480 470 ……
(1)以x作为点的横坐标,p作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连结各点所得的图形,判断p与x的函数关系式;
(2)如果这种运动服的买入件为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?
22、(12分)九(2)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
图案(1) 图案(2) 图案(3)
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是____________ m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为m,长方形框架ABCD的面积为S= ________(用含的代数式表示);当AB=_________m时, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为m, 设AB为m,当AB=________m时, 长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.
探索: 如图案(4), 如果铝合金材料总长度为m共有n条竖档时, 那么当竖档AB多少时,长方形框架ABCD的面积最大.
23、(14分)如图①②,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米).
答案:一、
1 2 3 4 5 6 7 8 9 10
D B D B C A B B B A
二、填空
11、12、 ,2 13、 14、100
三、15、解:原式
16、解:(1)如图.
(2)如图,因为DE,AF都垂直于地面,且光线DF∥AC,所以Rt△DEF∽Rt△ABC.所以.所以.所以AB=11(m).即建筑物AB的高为.
17、
18、(1)BE=DF或OE=OF,
(2)OE=OF=OA或OE=OF=OC或OE=OF且AC=EF,
略证:因为OA=OE=OF=OC则,EF=AC 所以四边形A ECF是矩形
解:设OA=xcm, 则OD=(14+x)cm, OE=(10.3+x)cm………………1分
在Rt△ODE中,∠ODE=67°.
∵sin∠ODE= ∴=0.92 …………5分
∴x=32.25
OA≈32.3(cm). …………………………7分
答:半径OA的长约为32.3cm. ………………… 8分
19、解:(1)如图1,连结OC,∵OP⊥CD
∴CP=CD= ,∴CD=2…………… 6分
(2)∵∠PEO=45°,OE=2,BE=3,
∴将直线CD绕着点E逆时针旋转45°后,若再沿射线EB平移3个单位,直线CD与⊙O相切于B,或再沿射线EA平移7个单位,直线CD与⊙O相切于A (如图2) …………… 12分
解:(1)p与x成一次函数关系。 设函数关系式为p=kx+b ,则 解得:k=-10,b=1000 , ∴ p=-10x+1000 经检验可知:当x=52,
p=480,当x=53,p=470时也适合这一关系式
∴所求的函数关系为p=-10x+1000
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000)
∴ y=-10x2+1400x-40000
(3)由y=-10x2+1400x-40000 可知,当时,y有最大值
∴ 卖出价格为70元时,能花得最大利润。
解:(1), (2)-x2+2x ,1, ,
(3)设AB长为m,那么AD为,
S=·=-,
当=时,S最大.
22、
(1)连结OC,∵EF切⊙O于点C,∴OC⊥EF,∴∠1+∠4 =90°
∵AD⊥EF, ∴在Rt△ACD中,∠3+∠4=90°
又 ∵OA=OC, ∴∠1=∠2, ∴∠2 =∠3 即∠DAC=∠BAC
(2)∠BAG=∠DAC,理由如下:
连结BC,∵AB为⊙O的直径,∴∠BCA=90°,∠B+∠BAC=90°
在Rt△AGD中,∠AGD+∠GAD=90°,
又 ∵∠B=∠AGD. ∴∠BAC=∠GAD,
即 ∠BAG+∠GAC=∠GAC+∠DAC,
∴∠BAG=∠DAC
23、【解】过M作AC平行的直线,与OA,FC分别相交于H,N.(1)在Rt△OHM中,∠OHM=90°,OM=5,HM=OM×sinα=3,所以OH=4,MB=HA=5-4=1(单位),1×5=5(cm),所以铁环钩离地面的高度为5cm.
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH=α,所以=sinα=,即得FN=FM,在Rt△FMN中,∠FNM=90°,MN=BC=AC-AB=11-3=8(单位),由勾股定理FM2=FN2+MN2,即FM2=(FM)2+82,解得FM=10(单位),10×5=50(cm),所以铁环钩的长度FM为50cm.
考号 姓名 班级
………………………………装………………………………………订……………………………………线………………………………
P
B
A
O
图3
E
D
A
C
B
E
C
D
A
F
B
图5
A
B
p(件)
500
490
480
470
50 51 52 53 x(元/件)
A
B
M
O
F
C
②
①
H
N
A
B
F
C
D
E
同课章节目录
