2020-2021学年北师大版七年级数学下册第五章 生活中的轴对称 单元同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第五章 生活中的轴对称 单元同步练习题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 270.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-12 00:00:00 | ||
图片预览

文档简介
2020-2021学年北师大版七年级数学下册第五章
生活中的轴对称
单元同步练习题
A组(基础题)
一、填空题
1.(1)如图,在2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有______个.
(2)如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,且AB=8
cm,则△DEB的周长为______cm.
2.(1)如图,在△ABC中,点D,E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是______.
(2)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为______cm.
3.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=______.
4.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于点E,OE=.如果P是OB上一动点,则线段MP的取值范围是______.
二、选择题
5.下列图形中,是轴对称图形的是(
)
A B C D
6.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是(
)
A.50°
B.40°
C.30°
D.20°
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=6,AB=16,则△ABD的面积为(
)
A.16
B.32
C.48
D.60
8.如图,已知D,E是BC边上的点,且BD=CE,下列条件不能判定△ABE≌△ACD的是(C)
A.AB=AC
B.AD=AE
C.BE=CD
D.∠BDA=∠CEA
三、解答题
9.(1)如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.
(2)如图,在Rt△ABC中,已知∠ACB=90°
,AC=BC,D是斜边的中点,经过点C引一条直线l(不与AC,BC重合并且不经过点D),经过点A作AE⊥l,经过点B作BF⊥l,连接DE,DF,猜想△DEF的形状并证明.
10.(1)如图,在△ABC中,AB=AC,D是BC的中点,过点A的直线EF∥BC,且AE=AF,连接DE,DF,求证:DE=DF.
证明:如图,连接AD,∵AB=AC,D是BC的中点,
(2)在△ABC中,∠ACB=90
,AC=BC,点D为线段AC上的一点(不和点A,C重合)点E在线段BD的延长线上,点F在线段BD上,连接CE,CF,AE,且∠ECF=90°,CE=CF,过点F作FG⊥BD,分别交线段BC、线段AC的延长线于点P,G.
①如图1,求证:AC=CG;
②如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.
图1 图2
B组(中档题)
一、填空题
11.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28
cm2,AB=16
cm,AC=12
cm,则DE的长为_____cm.
12.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠CDO+∠CFO=88°,则∠C=______.
13.如图,在△ABC中,点D为AC的中点,∠ABC的平分线与AC的垂直平分线交于点E,连接DE,过点E分别作AB,BC所在直线的垂线,垂足分别为M,N.若AM=2
cm,AB=3.2
cm,则BC的长为______cm.
二、解答题
14.如图,O为△ABC内部一点,OB=3,P,R为点O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于7?并说明PR的长度在此时会等于7的理由.
(2)在(1)的情况下,当∠ABC不是你指出的角度时,PR的长度是小于7还是大于7?说明你判断的理由.
C组(综合题)
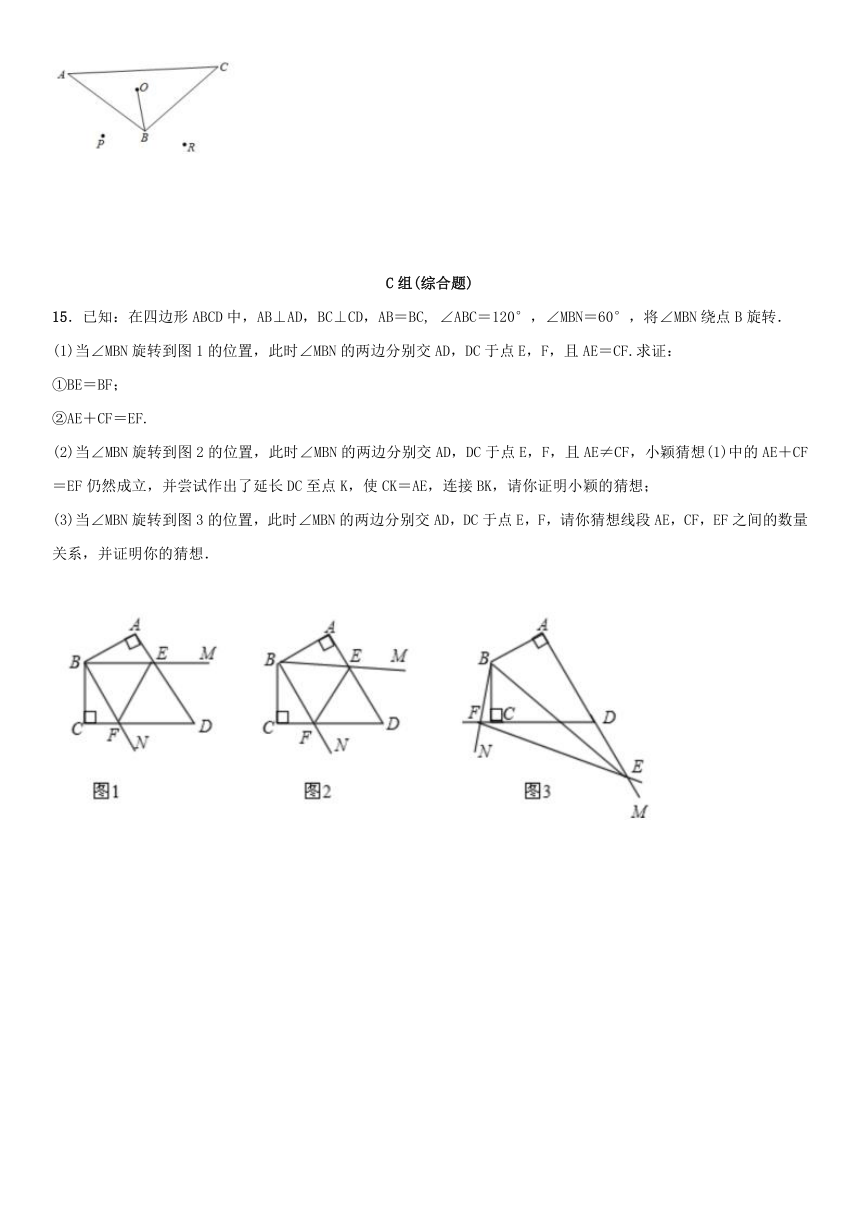
15.已知:在四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,
∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转.
(1)当∠MBN旋转到图1的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE=CF.求证:
①BE=BF;
②AE+CF=EF.
(2)当∠MBN旋转到图2的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE≠CF,小颖猜想(1)中的AE+CF=EF仍然成立,并尝试作出了延长DC至点K,使CK=AE,连接BK,请你证明小颖的猜想;
(3)当∠MBN旋转到图3的位置,此时∠MBN的两边分别交AD,DC于点E,F,请你猜想线段AE,CF,EF之间的数量关系,并证明你的猜想.
参考答案
2020-2021学年北师大版七年级数学下册第五章
生活中的轴对称
单元同步练习题
A组(基础题)
一、填空题
1.(1)如图,在2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有3个.
(2)如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,且AB=8
cm,则△DEB的周长为8cm.
2.(1)如图,在△ABC中,点D,E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是120°.
(2)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为2cm.
3.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=2∶3∶4.
4.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于点E,OE=.如果P是OB上一动点,则线段MP的取值范围是MP≥1.
二、选择题
5.下列图形中,是轴对称图形的是(C)
A B C D
6.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是(D)
A.50°
B.40°
C.30°
D.20°
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=6,AB=16,则△ABD的面积为(C)
A.16
B.32
C.48
D.60
8.如图,已知D,E是BC边上的点,且BD=CE,下列条件不能判定△ABE≌△ACD的是(C)
A.AB=AC
B.AD=AE
C.BE=CD
D.∠BDA=∠CEA
三、解答题
9.(1)如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.
证明:过点D作DE⊥BC于点E,过点D作DF⊥AB交BA的延长线于点F.
∵BD平分∠ABC,
∴DE=DF,∠DEC=∠F=90°.
在Rt△CDE和Rt△ADF中,
∴Rt△CDE≌Rt△ADF(HL).
∴∠C=∠FAD.
∴∠BAD+∠C=∠BAD+∠FAD=180°.
(2)如图,在Rt△ABC中,已知∠ACB=90°
,AC=BC,D是斜边的中点,经过点C引一条直线l(不与AC,BC重合并且不经过点D),经过点A作AE⊥l,经过点B作BF⊥l,连接DE,DF,猜想△DEF的形状并证明.
解:△DEF为等腰直角三角形.
证明:连接CD.
∵AE⊥CE,BF⊥CE,
∴∠AEC=∠BFC=90°.
∵∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACE=∠CBF.
在△ACE和△CBF中,
∴△ACE≌△CBF(AAS).
∴AE=CF,∠CAE=∠BCF.
∵∠CAB=∠DCB=45°,
∴∠DAE=∠DCF.
又∵AD=CD,
∴△AED≌△CFD(SAS).
∴ED=FD,∠ADE=∠CDF.
∴∠EDF=∠ADE+∠ADF=∠CDF+∠ADF=90°.
∴△DEF为等腰直角三角形.
10.(1)如图,在△ABC中,AB=AC,D是BC的中点,过点A的直线EF∥BC,且AE=AF,连接DE,DF,求证:DE=DF.
证明:如图,连接AD,∵AB=AC,D是BC的中点,
∴AD⊥BC.
∵EF∥BC,
∴AD⊥EF.
又∵AE=AF,
∴AD是EF的垂直平分线.
∴DE=DF.
(2)在△ABC中,∠ACB=90
,AC=BC,点D为线段AC上的一点(不和点A,C重合)点E在线段BD的延长线上,点F在线段BD上,连接CE,CF,AE,且∠ECF=90°,CE=CF,过点F作FG⊥BD,分别交线段BC、线段AC的延长线于点P,G.
①如图1,求证:AC=CG;
②如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.
图1 图2
证明:①∵∠BCG=180°-∠ACB=90°=∠ECF,
∴∠BCG+∠BCF=∠ECF+∠BCF,
即∠FCG=∠ECB.
∵FG⊥BD,∴∠DFG=90°,∴∠DBC+∠BDG=90°.
又∵∠DGF+∠BDG=90°,∴∠DBC=∠DGF.
在△BCE和△GCF中,
∴△BCE≌△GCF(AAS).∴CB=CG.
又∵AC=CB,∴AC=CG.
②在△BDC和△GPC中,
∴△BDC≌△GPC(ASA).∴CD=CP.
∵AC=BC,∴AD=BP.
∵AC=BC,∴∠BAC=∠ABC.
在△AHD和△BHP中,
∴△AHD≌△BHP(SAS).
∴∠BHG=∠AHD.
B组(中档题)
一、填空题
11.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28
cm2,AB=16
cm,AC=12
cm,则DE的长为2cm.
12.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠CDO+∠CFO=88°,则∠C=46°.
13.如图,在△ABC中,点D为AC的中点,∠ABC的平分线与AC的垂直平分线交于点E,连接DE,过点E分别作AB,BC所在直线的垂线,垂足分别为M,N.若AM=2
cm,AB=3.2
cm,则BC的长为7.2cm.
二、解答题
14.如图,O为△ABC内部一点,OB=3,P,R为点O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于7?并说明PR的长度在此时会等于7的理由.
(2)在(1)的情况下,当∠ABC不是你指出的角度时,PR的长度是小于7还是大于7?说明你判断的理由.
解:(1)∠ABC=90°时,PR=7.
理由如下:连接PB,RB,
∵点P,R为点O分别以直线AB、直线BC为对称轴的对称点,
∴PB=OB=3,RB=OB=3,∠ABP=∠ABD,∠CBR=∠CBO.
∵∠ABC=90°,
∴∠ABP+∠CBR+∠ABO+∠CBO=2∠ABC=180°.
∴P,B,R三点共线.∴PR=PB+BR=7.
(2)PR的长度小于7.
理由如下:当∠ABC≠90°时,
则点P,B,R三点不在同一直线上,
连接PR,
∴PB+BR>PR.
∵PB+BR=2OB=2×3=7,∴PR<7.
C组(综合题)
15.已知:在四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,
∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转.
(1)当∠MBN旋转到图1的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE=CF.求证:
①BE=BF;
②AE+CF=EF.
(2)当∠MBN旋转到图2的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE≠CF,小颖猜想(1)中的AE+CF=EF仍然成立,并尝试作出了延长DC至点K,使CK=AE,连接BK,请你证明小颖的猜想;
(3)当∠MBN旋转到图3的位置,此时∠MBN的两边分别交AD,DC于点E,F,请你猜想线段AE,CF,EF之间的数量关系,并证明你的猜想.
解:(1)证明:①在△ABE和△CBF中,
∴△ABE≌△CBF(SAS).∴BE=BF.
②由①知△ABE≌△CBF,
∴∠ABE=∠CBF=(∠ABC-∠MBN)=(120°-60°)=30°.
∴AE=BE,CF=BF.
∵BE=BF,∠MBN=60°,
∴△BEF是等边三角形.
∴BE=BF=EF.
∴AE+CF=BE+BF=EF.
(2)证明:延长DC至点K,使得CK=AE,连接BK.
在△ABE和△CBK中,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC.
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,即∠KBE=120°.
∵∠EBF=60°,∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
∴△EBF≌△KBF(SAS).∴EF=KF.
∵KF=CK+CF,∴AE+CF=EF.
(3)猜想:AE-CF=EF.
证明:在DC的延长线上取点K,使CK=AE,连接BK.
在△ABE和△CBK中,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC.
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,即∠KBE=120°.
∵∠EBF=60°,∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
∴△EBF≌△KBF(SAS).∴EF=KF.
∵KF=CK-CF,∴AE-CF=EF.
生活中的轴对称
单元同步练习题
A组(基础题)
一、填空题
1.(1)如图,在2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有______个.
(2)如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,且AB=8
cm,则△DEB的周长为______cm.
2.(1)如图,在△ABC中,点D,E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是______.
(2)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为______cm.
3.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=______.
4.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于点E,OE=.如果P是OB上一动点,则线段MP的取值范围是______.
二、选择题
5.下列图形中,是轴对称图形的是(
)
A B C D
6.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是(
)
A.50°
B.40°
C.30°
D.20°
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=6,AB=16,则△ABD的面积为(
)
A.16
B.32
C.48
D.60
8.如图,已知D,E是BC边上的点,且BD=CE,下列条件不能判定△ABE≌△ACD的是(C)
A.AB=AC
B.AD=AE
C.BE=CD
D.∠BDA=∠CEA
三、解答题
9.(1)如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.
(2)如图,在Rt△ABC中,已知∠ACB=90°
,AC=BC,D是斜边的中点,经过点C引一条直线l(不与AC,BC重合并且不经过点D),经过点A作AE⊥l,经过点B作BF⊥l,连接DE,DF,猜想△DEF的形状并证明.
10.(1)如图,在△ABC中,AB=AC,D是BC的中点,过点A的直线EF∥BC,且AE=AF,连接DE,DF,求证:DE=DF.
证明:如图,连接AD,∵AB=AC,D是BC的中点,
(2)在△ABC中,∠ACB=90
,AC=BC,点D为线段AC上的一点(不和点A,C重合)点E在线段BD的延长线上,点F在线段BD上,连接CE,CF,AE,且∠ECF=90°,CE=CF,过点F作FG⊥BD,分别交线段BC、线段AC的延长线于点P,G.
①如图1,求证:AC=CG;
②如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.
图1 图2
B组(中档题)
一、填空题
11.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28
cm2,AB=16
cm,AC=12
cm,则DE的长为_____cm.
12.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠CDO+∠CFO=88°,则∠C=______.
13.如图,在△ABC中,点D为AC的中点,∠ABC的平分线与AC的垂直平分线交于点E,连接DE,过点E分别作AB,BC所在直线的垂线,垂足分别为M,N.若AM=2
cm,AB=3.2
cm,则BC的长为______cm.
二、解答题
14.如图,O为△ABC内部一点,OB=3,P,R为点O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于7?并说明PR的长度在此时会等于7的理由.
(2)在(1)的情况下,当∠ABC不是你指出的角度时,PR的长度是小于7还是大于7?说明你判断的理由.
C组(综合题)
15.已知:在四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,
∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转.
(1)当∠MBN旋转到图1的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE=CF.求证:
①BE=BF;
②AE+CF=EF.
(2)当∠MBN旋转到图2的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE≠CF,小颖猜想(1)中的AE+CF=EF仍然成立,并尝试作出了延长DC至点K,使CK=AE,连接BK,请你证明小颖的猜想;
(3)当∠MBN旋转到图3的位置,此时∠MBN的两边分别交AD,DC于点E,F,请你猜想线段AE,CF,EF之间的数量关系,并证明你的猜想.
参考答案
2020-2021学年北师大版七年级数学下册第五章
生活中的轴对称
单元同步练习题
A组(基础题)
一、填空题
1.(1)如图,在2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有3个.
(2)如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB于点E,且AB=8
cm,则△DEB的周长为8cm.
2.(1)如图,在△ABC中,点D,E在BC上,且BD=DE=AD=AE=EC,则∠BAC的度数是120°.
(2)如图,在△ABC中,AB=AC,∠A=120°,BC=6
cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为2cm.
3.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO=2∶3∶4.
4.如图,点M是∠AOB平分线上一点,∠AOB=60°,ME⊥OA于点E,OE=.如果P是OB上一动点,则线段MP的取值范围是MP≥1.
二、选择题
5.下列图形中,是轴对称图形的是(C)
A B C D
6.如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是(D)
A.50°
B.40°
C.30°
D.20°
7.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交边AC,AB于点M,N,再分别以点M,N为圆心,大于MN长为半径画弧,两弧交于点P,作射线AP交边BC于点D.若CD=6,AB=16,则△ABD的面积为(C)
A.16
B.32
C.48
D.60
8.如图,已知D,E是BC边上的点,且BD=CE,下列条件不能判定△ABE≌△ACD的是(C)
A.AB=AC
B.AD=AE
C.BE=CD
D.∠BDA=∠CEA
三、解答题
9.(1)如图,在四边形ABCD中,BC>BA,AD=CD,BD平分∠ABC,求证:∠A+∠C=180°.
证明:过点D作DE⊥BC于点E,过点D作DF⊥AB交BA的延长线于点F.
∵BD平分∠ABC,
∴DE=DF,∠DEC=∠F=90°.
在Rt△CDE和Rt△ADF中,
∴Rt△CDE≌Rt△ADF(HL).
∴∠C=∠FAD.
∴∠BAD+∠C=∠BAD+∠FAD=180°.
(2)如图,在Rt△ABC中,已知∠ACB=90°
,AC=BC,D是斜边的中点,经过点C引一条直线l(不与AC,BC重合并且不经过点D),经过点A作AE⊥l,经过点B作BF⊥l,连接DE,DF,猜想△DEF的形状并证明.
解:△DEF为等腰直角三角形.
证明:连接CD.
∵AE⊥CE,BF⊥CE,
∴∠AEC=∠BFC=90°.
∵∠ACE+∠BCF=90°,∠BCF+∠CBF=90°,
∴∠ACE=∠CBF.
在△ACE和△CBF中,
∴△ACE≌△CBF(AAS).
∴AE=CF,∠CAE=∠BCF.
∵∠CAB=∠DCB=45°,
∴∠DAE=∠DCF.
又∵AD=CD,
∴△AED≌△CFD(SAS).
∴ED=FD,∠ADE=∠CDF.
∴∠EDF=∠ADE+∠ADF=∠CDF+∠ADF=90°.
∴△DEF为等腰直角三角形.
10.(1)如图,在△ABC中,AB=AC,D是BC的中点,过点A的直线EF∥BC,且AE=AF,连接DE,DF,求证:DE=DF.
证明:如图,连接AD,∵AB=AC,D是BC的中点,
∴AD⊥BC.
∵EF∥BC,
∴AD⊥EF.
又∵AE=AF,
∴AD是EF的垂直平分线.
∴DE=DF.
(2)在△ABC中,∠ACB=90
,AC=BC,点D为线段AC上的一点(不和点A,C重合)点E在线段BD的延长线上,点F在线段BD上,连接CE,CF,AE,且∠ECF=90°,CE=CF,过点F作FG⊥BD,分别交线段BC、线段AC的延长线于点P,G.
①如图1,求证:AC=CG;
②如图2,延长线段GF交线段AB于点H,连接DH,当AH=BH时,求证:∠BHG=∠AHD.
图1 图2
证明:①∵∠BCG=180°-∠ACB=90°=∠ECF,
∴∠BCG+∠BCF=∠ECF+∠BCF,
即∠FCG=∠ECB.
∵FG⊥BD,∴∠DFG=90°,∴∠DBC+∠BDG=90°.
又∵∠DGF+∠BDG=90°,∴∠DBC=∠DGF.
在△BCE和△GCF中,
∴△BCE≌△GCF(AAS).∴CB=CG.
又∵AC=CB,∴AC=CG.
②在△BDC和△GPC中,
∴△BDC≌△GPC(ASA).∴CD=CP.
∵AC=BC,∴AD=BP.
∵AC=BC,∴∠BAC=∠ABC.
在△AHD和△BHP中,
∴△AHD≌△BHP(SAS).
∴∠BHG=∠AHD.
B组(中档题)
一、填空题
11.如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是28
cm2,AB=16
cm,AC=12
cm,则DE的长为2cm.
12.如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO.若∠CDO+∠CFO=88°,则∠C=46°.
13.如图,在△ABC中,点D为AC的中点,∠ABC的平分线与AC的垂直平分线交于点E,连接DE,过点E分别作AB,BC所在直线的垂线,垂足分别为M,N.若AM=2
cm,AB=3.2
cm,则BC的长为7.2cm.
二、解答题
14.如图,O为△ABC内部一点,OB=3,P,R为点O分别以直线AB、直线BC为对称轴的对称点.
(1)请指出当∠ABC为多少度时,会使得PR的长度等于7?并说明PR的长度在此时会等于7的理由.
(2)在(1)的情况下,当∠ABC不是你指出的角度时,PR的长度是小于7还是大于7?说明你判断的理由.
解:(1)∠ABC=90°时,PR=7.
理由如下:连接PB,RB,
∵点P,R为点O分别以直线AB、直线BC为对称轴的对称点,
∴PB=OB=3,RB=OB=3,∠ABP=∠ABD,∠CBR=∠CBO.
∵∠ABC=90°,
∴∠ABP+∠CBR+∠ABO+∠CBO=2∠ABC=180°.
∴P,B,R三点共线.∴PR=PB+BR=7.
(2)PR的长度小于7.
理由如下:当∠ABC≠90°时,
则点P,B,R三点不在同一直线上,
连接PR,
∴PB+BR>PR.
∵PB+BR=2OB=2×3=7,∴PR<7.
C组(综合题)
15.已知:在四边形ABCD中,AB⊥AD,BC⊥CD,AB=BC,
∠ABC=120°,∠MBN=60°,将∠MBN绕点B旋转.
(1)当∠MBN旋转到图1的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE=CF.求证:
①BE=BF;
②AE+CF=EF.
(2)当∠MBN旋转到图2的位置,此时∠MBN的两边分别交AD,DC于点E,F,且AE≠CF,小颖猜想(1)中的AE+CF=EF仍然成立,并尝试作出了延长DC至点K,使CK=AE,连接BK,请你证明小颖的猜想;
(3)当∠MBN旋转到图3的位置,此时∠MBN的两边分别交AD,DC于点E,F,请你猜想线段AE,CF,EF之间的数量关系,并证明你的猜想.
解:(1)证明:①在△ABE和△CBF中,
∴△ABE≌△CBF(SAS).∴BE=BF.
②由①知△ABE≌△CBF,
∴∠ABE=∠CBF=(∠ABC-∠MBN)=(120°-60°)=30°.
∴AE=BE,CF=BF.
∵BE=BF,∠MBN=60°,
∴△BEF是等边三角形.
∴BE=BF=EF.
∴AE+CF=BE+BF=EF.
(2)证明:延长DC至点K,使得CK=AE,连接BK.
在△ABE和△CBK中,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC.
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,即∠KBE=120°.
∵∠EBF=60°,∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
∴△EBF≌△KBF(SAS).∴EF=KF.
∵KF=CK+CF,∴AE+CF=EF.
(3)猜想:AE-CF=EF.
证明:在DC的延长线上取点K,使CK=AE,连接BK.
在△ABE和△CBK中,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC.
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,即∠KBE=120°.
∵∠EBF=60°,∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
∴△EBF≌△KBF(SAS).∴EF=KF.
∵KF=CK-CF,∴AE-CF=EF.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
