9.3 反比例函数的应用 课件2

(共14张PPT)
反比例函数是刻画现实问题中数量关系的一种数学模型,它与一次函数和正比例函数一样,在生活生产实际中也有着广泛的应用.
已知矩形的面积是60cm .
（1）矩形的长a（cm）与宽b（cm）有怎样的函数关系？
（2）如果矩形的宽为4 cm，那么矩形的长为多少cm？
（3）如果矩形的长至多为12 cm，那么矩形的宽至少是多少cm？
气球内充满一定质量的气体，当温度不变时，气球内气体的气压P（kpa）是气体体积V（m ）的反比例函数.当V =0.8 m 时, P=125 kpa.
(1)求P与V的函数关系式.
(2)当气球内气体的气压大于150kpa时,气球将爆炸,为了安全起见,气体体积至少为多少m
(保留两个有效数字)
练一 练
1、某蓄水池的排水管每小时排水8m3 ，6h可将满池水全部排空。
⑴蓄水池的容积是多少？____________
⑵如果增加排水管。使每小时排水量达到
Q（m3），那么将满池水排空所需时间t（h）
将如何变化？__________
⑶写出t与Q之间关系式。____________
⑷如果准备在5小时内将满池水排空，那么
每小时的排水量至少为____________。
⑸已知排水管最多为每小时12 m3，则至少__________h可将满池水全部排空。
你一定行
例1、小明将一篇24000字的社会调查报告录入电脑，打印成文。
（1）如果小明以每分种120字的速度录入，他需要多少时间才能完成录入任务？
（2）录入文字的速度v（字/min）与完成录入的时间t(min)有怎样的函数关系？
（3）小明希望能在3h内完成录入任务，那么他每分钟至少应录入多少个字？
驶向胜利的彼岸
例2某自来水公司计划新建一个容积 为 的 长方形蓄水池。
(1)蓄水池的底部s(㎡)与其深度h(m)有怎样的函数关系？
(2)如果蓄水池的深度设计为5m，那么蓄水池的底面积应为多少平方米？
(3)由于绿化以及辅助用地的需要，经过实地测量，蓄水池的长与宽最多只能设计为100m和60m，那么蓄水池的深度至少达到多少才能满足要求？（保留两位小数）
驶向胜利的彼岸
随堂练习
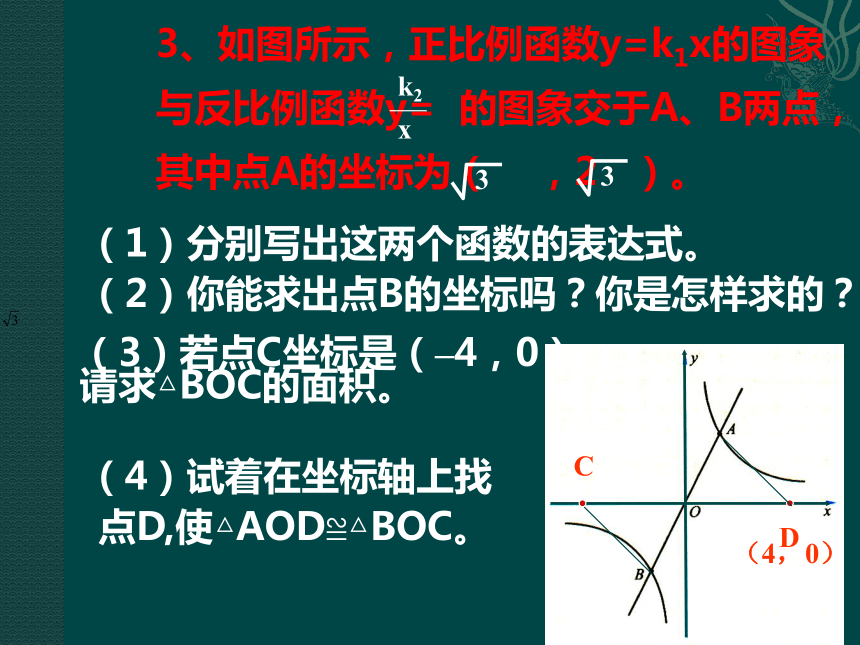
（4）试着在坐标轴上找
点D,使△AOD≌△BOC。
（1）分别写出这两个函数的表达式。
（2）你能求出点B的坐标吗？你是怎样求的？
（3）若点C坐标是（–4，0）. 请求△BOC的面积。
3、如图所示，正比例函数y=k1x的图象与反比例函数y= 的图象交于A、B两点，其中点A的坐标为（ ，2 ）。
3
3
k2
x
C
D
（4，0）
题．
编一道生活中的数学问
根据反比例函数
x
y
1200
=
为了预防“非典”,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.
(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,
学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低
于3mg且持续时间不低于10min时,才能有效杀
灭空气中的病菌,那么此次消毒是否有效 为什么
开启 智慧
制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，设该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．
（1）分别求出将材料加热和停止加热
进行操作时，y与x的函数关系式；
（2）根据工艺要求，当材料的温度低
于15℃时，须停止操作，那么从开始加
热到停止操作，共经历了多少时间？
中考题
难不倒
牵一发而动全身

函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.
从函数的图象中获取信息的能力是学好数学必需具有的基本素质.
下课了!
结束寄语