河南省信阳高中2020-2021学年高一4月月考数学(文)试卷 Word版含答案
文档属性
| 名称 | 河南省信阳高中2020-2021学年高一4月月考数学(文)试卷 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 09:00:50 | ||
图片预览



文档简介
信阳高级中学2023届高一下期月考
数学(文)试题
第I卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知集合A={x|-1 A.{1,2} B.{0,1,2} C.{-1,0,1,2} D.{0,1,2,3}
2、若false,则点false位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等( ).
A.9 B.10 C.12 D.13
4、体育教师指导4个学生训练转身动作,预备时,4个学生全部面朝正南方向站成一排。训练时,每次都让3个学生“向后转”,若4个学生全部转到面朝正北方向,则至少需要“向后转”的次数是
A.3 B.4 C.5 D.6
5、已知角false终边上一点false的坐标为false(false),则false的值是( )
A. 2 B. -2 C. false D. false
4465320488956、某几何体的三视图如图所示,则该几何体的表面积是( )
45593002478405第7题图
第7题图
0000正视图
俯视图
侧视图
2
2
1
2
1
A. B. C. D.
7、德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国。在我国科技水平业已落后的情况下,我国数学家、天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河。如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入n=10,则输出的结果是( )
A.false B.false
C.false D. false
8、函数false 的单调递增区间是( )
A.(-∞,-2) B. (-∞,-1) C.(1, +∞) D. (4, +∞)
9、若a=0.50.6,b=0.60.5,c=20.5,则下列结论正确的是( )
A.b>c>a B.c>a>b C.a>b>c D.c>b>a
10、在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1,DD1的中点,则异面直线AF,DE所成角的余弦值为( )
A. B. C. D.
11、在区间false上随机取一个数x,false的值介于0到false之间的概率为( )
A.false B.false C.false D.false
12.
二、填空题:(本题共4小题。每小题5分,共20分)
13.函数的定义域是 .
14.当false时,false,则实数a的取值范围是________.
16.在三棱锥P-ABC中,PA=PC=2,BA=BC=1,∠ABC=90°,若PA与底面ABC所成的角为60°,则点P到底面ABC的距离是_______;三棱锥P-ABC的外接球的表面积
.(本题第一空2分,第二空3分)
三、解答题(17题10分,18-22题每题12分,共70分)
17、(10分)
(1)
(2) 已知false,且false是第一象限角。求false的值。
18、(12分)
19、(12分)若养殖场每个月生猪的死亡率不超过1%,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001);
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程false中斜率和截距用最小二乘法估计计算公式如下:
false 参考数据:false。
39439851016020、(12分)在三棱柱ABC-A1B1C1中,四边形A1B1BA是菱形,AB=4,∠ABB1=60°,B1C1=3,BC⊥AB,点M、N分别是A1B、AC1的中点,且MN⊥AB1。
(1)求证:平面BCC1B1⊥平面A1B1BA;
(2)求四棱锥A-BCC1B1的体积。
21.(12分)在平面直角坐标系中,已知圆心在轴上、半径为的圆位于轴右侧,且与直线相切.
(1)求圆的方程;
(2)在圆上,是否存在点,使得直线与圆相交于不同的两点,且的面积最大?若存在,求出点的坐标及对应的的面积;若不存在,请说明理由.
22、已知函数false.
(1)若false成立,求的取值范围;
(2)若定义在false上奇函数满足false,且当false时,,求false 在false上的解析式,并写出false在false上的单调区间(不必证明);
(3)对于(Ⅱ)中的false,若关于false的不等式false在false上恒成立,求实数false的取值范围.
2023届高一下期周考(二)
数学(文)参考答案
1、B 2、D 3、D 4、B 5、D 6、A 7、B 8、D 9、D 10、B 11、A 12、B
13、false 14、false 16、false
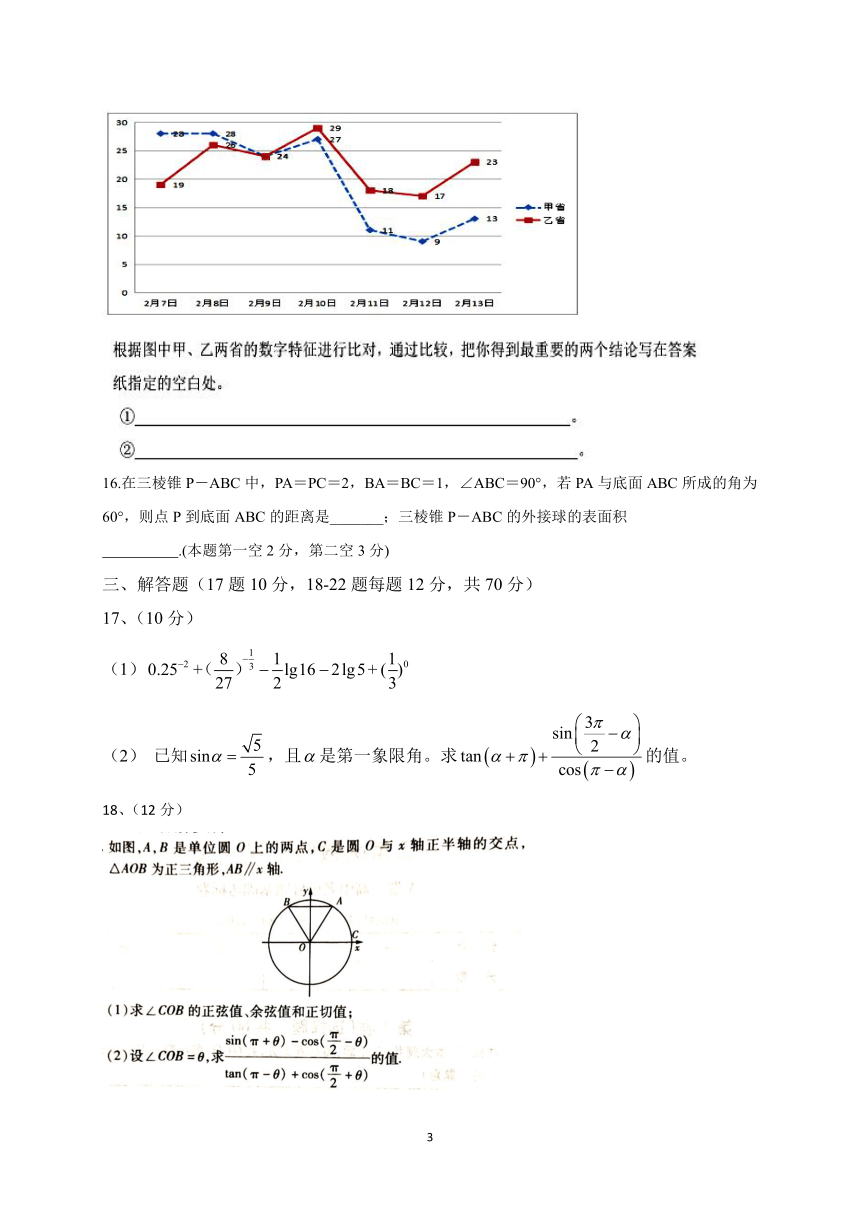
15、开放性试题,如甲省比乙省的新增人数的平均数低:甲省比乙省的方差要大:
17、(1) (2)因为false是第一象限角,所以false.
因为false.所以false.因为false.
所以false.
21、(1)设圆心是,它到直线的距离是,
解得或(舍去) 2分
所求圆的方程是 4分
(2)点在圆上
,且
又原点到直线的距离 6分
解得 7分
而 9分
10分
当,即时取得最大值,
此时点的坐标是与,面积的最大值是. 12分
22、(Ⅰ)由false得false,解得false,所以x的取值范围是false;
(Ⅱ)当-3≤x≤-2时,g(x)=-g(x+2)=g(-x-2)
=f(-x-2)=false,
当-2<x≤-1时,g(x)=-g(x+2)=-f(x+2)=-false,
综上可得false
false在false和false上递减;false在false上递增;
(Ⅲ)因为false,由(Ⅱ)知,若g(x)=false,得x=false或false,由函数g(x)的图象可知若false在false上恒成立
记false
当false时,false,则
false 则false 解得false
当false时,false,则
false 则false 解得false
综上,故false
数学(文)试题
第I卷(选择题 共60分)
一、选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、已知集合A={x|-1
2、若false,则点false位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等( ).
A.9 B.10 C.12 D.13
4、体育教师指导4个学生训练转身动作,预备时,4个学生全部面朝正南方向站成一排。训练时,每次都让3个学生“向后转”,若4个学生全部转到面朝正北方向,则至少需要“向后转”的次数是
A.3 B.4 C.5 D.6
5、已知角false终边上一点false的坐标为false(false),则false的值是( )
A. 2 B. -2 C. false D. false
4465320488956、某几何体的三视图如图所示,则该几何体的表面积是( )
45593002478405第7题图
第7题图
0000正视图
俯视图
侧视图
2
2
1
2
1
A. B. C. D.
7、德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国。在我国科技水平业已落后的情况下,我国数学家、天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河。如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入n=10,则输出的结果是( )
A.false B.false
C.false D. false
8、函数false 的单调递增区间是( )
A.(-∞,-2) B. (-∞,-1) C.(1, +∞) D. (4, +∞)
9、若a=0.50.6,b=0.60.5,c=20.5,则下列结论正确的是( )
A.b>c>a B.c>a>b C.a>b>c D.c>b>a
10、在正方体ABCD﹣A1B1C1D1中,E,F分别为CC1,DD1的中点,则异面直线AF,DE所成角的余弦值为( )
A. B. C. D.
11、在区间false上随机取一个数x,false的值介于0到false之间的概率为( )
A.false B.false C.false D.false
12.
二、填空题:(本题共4小题。每小题5分,共20分)
13.函数的定义域是 .
14.当false时,false,则实数a的取值范围是________.
16.在三棱锥P-ABC中,PA=PC=2,BA=BC=1,∠ABC=90°,若PA与底面ABC所成的角为60°,则点P到底面ABC的距离是_______;三棱锥P-ABC的外接球的表面积
.(本题第一空2分,第二空3分)
三、解答题(17题10分,18-22题每题12分,共70分)
17、(10分)
(1)
(2) 已知false,且false是第一象限角。求false的值。
18、(12分)
19、(12分)若养殖场每个月生猪的死亡率不超过1%,则该养殖场考核为合格,该养殖场在2019年1月到8月养殖生猪的相关数据如下表所示:
(1)从该养殖场2019年2月到6月这5个月中任意选取3个月,求恰好有2个月考核获得合格的概率;
(2)根据1月到8月的数据,求出月利润y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.001);
(3)预计在今后的养殖中,月利润与月养殖量仍然服从(2)中的关系,若9月份的养殖量为1.5万只,试估计:该月利润约为多少万元?
附:线性回归方程false中斜率和截距用最小二乘法估计计算公式如下:
false 参考数据:false。
39439851016020、(12分)在三棱柱ABC-A1B1C1中,四边形A1B1BA是菱形,AB=4,∠ABB1=60°,B1C1=3,BC⊥AB,点M、N分别是A1B、AC1的中点,且MN⊥AB1。
(1)求证:平面BCC1B1⊥平面A1B1BA;
(2)求四棱锥A-BCC1B1的体积。
21.(12分)在平面直角坐标系中,已知圆心在轴上、半径为的圆位于轴右侧,且与直线相切.
(1)求圆的方程;
(2)在圆上,是否存在点,使得直线与圆相交于不同的两点,且的面积最大?若存在,求出点的坐标及对应的的面积;若不存在,请说明理由.
22、已知函数false.
(1)若false成立,求的取值范围;
(2)若定义在false上奇函数满足false,且当false时,,求false 在false上的解析式,并写出false在false上的单调区间(不必证明);
(3)对于(Ⅱ)中的false,若关于false的不等式false在false上恒成立,求实数false的取值范围.
2023届高一下期周考(二)
数学(文)参考答案
1、B 2、D 3、D 4、B 5、D 6、A 7、B 8、D 9、D 10、B 11、A 12、B
13、false 14、false 16、false
15、开放性试题,如甲省比乙省的新增人数的平均数低:甲省比乙省的方差要大:
17、(1) (2)因为false是第一象限角,所以false.
因为false.所以false.因为false.
所以false.
21、(1)设圆心是,它到直线的距离是,
解得或(舍去) 2分
所求圆的方程是 4分
(2)点在圆上
,且
又原点到直线的距离 6分
解得 7分
而 9分
10分
当,即时取得最大值,
此时点的坐标是与,面积的最大值是. 12分
22、(Ⅰ)由false得false,解得false,所以x的取值范围是false;
(Ⅱ)当-3≤x≤-2时,g(x)=-g(x+2)=g(-x-2)
=f(-x-2)=false,
当-2<x≤-1时,g(x)=-g(x+2)=-f(x+2)=-false,
综上可得false
false在false和false上递减;false在false上递增;
(Ⅲ)因为false,由(Ⅱ)知,若g(x)=false,得x=false或false,由函数g(x)的图象可知若false在false上恒成立
记false
当false时,false,则
false 则false 解得false
当false时,false,则
false 则false 解得false
综上,故false
同课章节目录
