任意角的三角函数(一)
图片预览


文档简介
(共14张PPT)
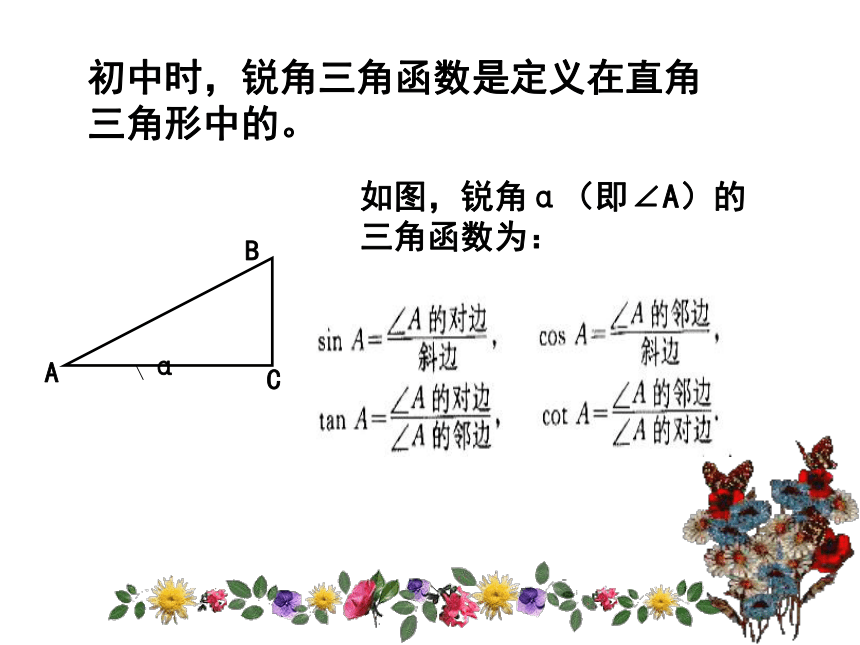
初中时,锐角三角函数是定义在直角三角形中的。
如图,锐角α(即∠A)的三角函数为:
A
B
C
α
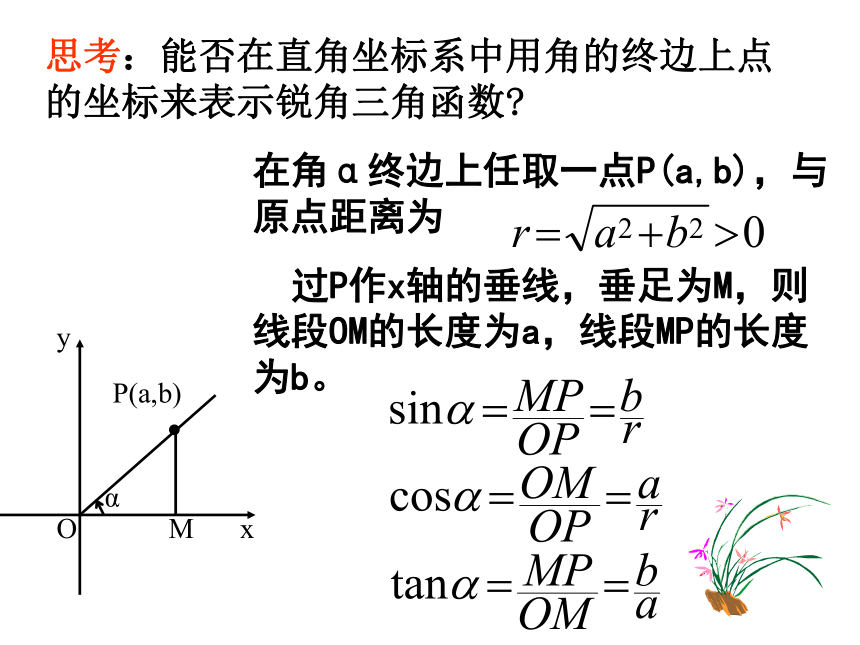
在角α终边上任取一点P(a,b),与原点距离为
过P作x轴的垂线,垂足为M,则线段OM的长度为a,线段MP的长度为b。
x
M
α
P(a,b)
O
y
思考:能否在直角坐标系中用角的终边上点的坐标来表示锐角三角函数
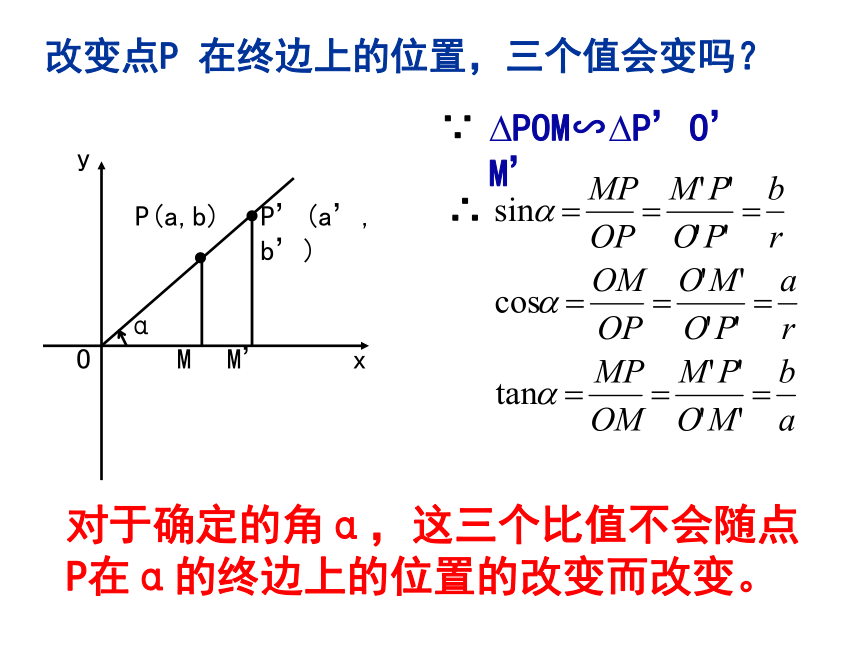
y
M
α
P(a,b)
O
x
M’
P’(a’,b’)
POM∽ P’O’M’
∵
∴
对于确定的角α,这三个比值不会随点P在α的终边上的位置的改变而改变。
改变点P 在终边上的位置,三个值会变吗?
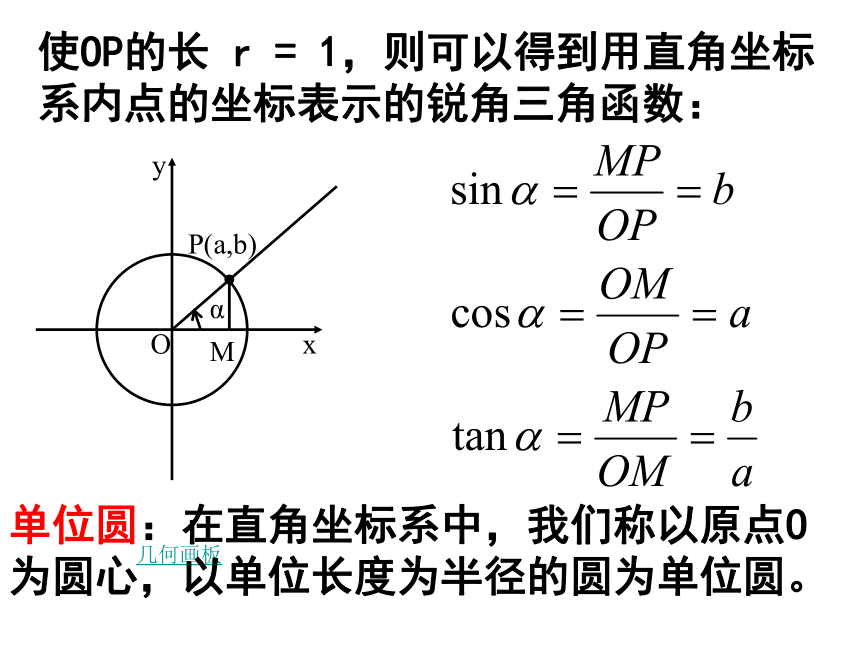
使OP的长 r = 1,则可以得到用直角坐标系内点的坐标表示的锐角三角函数:
y
α
P(a,b)
O
x
M
几何画板
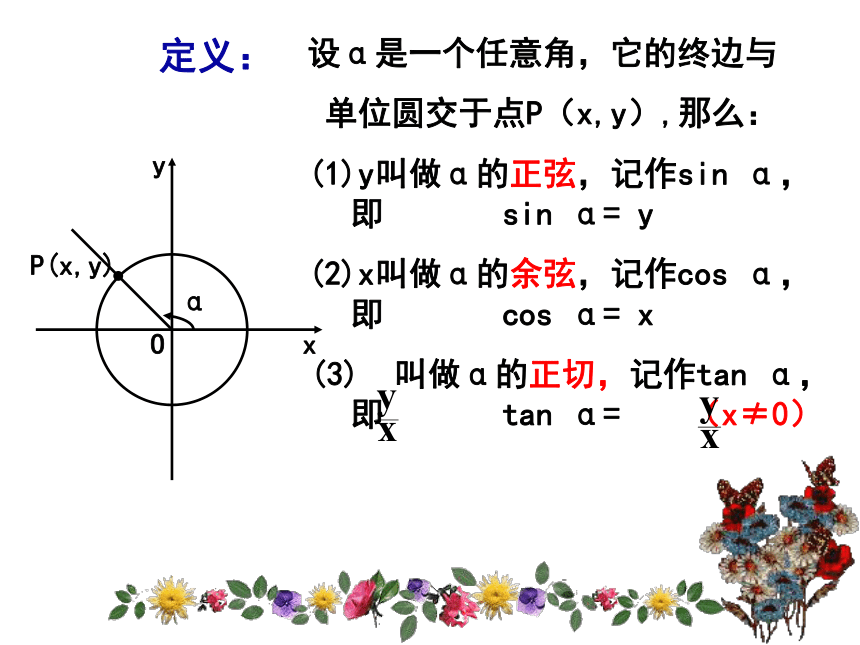
单位圆:在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆。
设α是一个任意角,它的终边与
单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sin α,即 sin α= y
(2)x叫做α的余弦,记作cos α,即 cos α= x
叫做α的正切,记作tan α,即 tan α= (x≠0)
定义:
α
P(x,y)
O
y
x
三角函数的概念
正弦、余弦、正切是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数
由于角的集合与实数集之间可以建立一一对应关系,故三角函数也可以看成实数为自变量的函数.
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
角
实数
三角函数值
例1 :求 的正弦,余弦和正切值。
解:在直角坐标系中,作∠AOB=
易知∠AOB的终边与单位圆的交点P
O
y
x
A
B
P
M
坐标为 ,所以
求 的正弦,余弦和正切值。
O
y
x
B
A
P
解:在直角坐标系中,作∠AOB=
易知∠AOB的终边与单位圆的交点坐
标为 ,所以
练习:
例2: 已知角α的终边经过点P0(-3,-4),求角α的正弦,余弦和正切值。
解:由已知可得:
设角α的终边与单位圆交于点P(x,y)
分别过点P, P0 作x轴的垂线MP,M0P0
于是,
O
y
x
P0(-3,-4)
M0
P(x,y)
M
则 |M0P0|=4,|OM0|=3,|MP|=-y,|OM|=-x,
△OMP∽△OM0P0,
设α是一个任意角,它的终边上任意一点P(x,y),
点P与原点的距离
那么:(1) 叫做α的正弦,记作sinα,即
sin α=
(2) 叫做α的余弦,记作cosα,即
cos α=
(3) 叫做α的正切, 记作tanα,即
tan α= (x≠0)
定义二:
探究:
三角函数 定义域
sinα
cosα
tanα
R
R
sinα
cosα
tanα
+
+
_
_
_
_
_
_
+
+
+
+
小结:
1、任意角三角函数的定义;
2、三角函数的定义域和函数值在各象限的符号(一全,二正,三切,四余).
作业:
P15 练习 1.2.3
初中时,锐角三角函数是定义在直角三角形中的。
如图,锐角α(即∠A)的三角函数为:
A
B
C
α
在角α终边上任取一点P(a,b),与原点距离为
过P作x轴的垂线,垂足为M,则线段OM的长度为a,线段MP的长度为b。
x
M
α
P(a,b)
O
y
思考:能否在直角坐标系中用角的终边上点的坐标来表示锐角三角函数
y
M
α
P(a,b)
O
x
M’
P’(a’,b’)
POM∽ P’O’M’
∵
∴
对于确定的角α,这三个比值不会随点P在α的终边上的位置的改变而改变。
改变点P 在终边上的位置,三个值会变吗?
使OP的长 r = 1,则可以得到用直角坐标系内点的坐标表示的锐角三角函数:
y
α
P(a,b)
O
x
M
几何画板
单位圆:在直角坐标系中,我们称以原点O为圆心,以单位长度为半径的圆为单位圆。
设α是一个任意角,它的终边与
单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sin α,即 sin α= y
(2)x叫做α的余弦,记作cos α,即 cos α= x
叫做α的正切,记作tan α,即 tan α= (x≠0)
定义:
α
P(x,y)
O
y
x
三角函数的概念
正弦、余弦、正切是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数
由于角的集合与实数集之间可以建立一一对应关系,故三角函数也可以看成实数为自变量的函数.
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,我们将它们统称为三角函数。
角
实数
三角函数值
例1 :求 的正弦,余弦和正切值。
解:在直角坐标系中,作∠AOB=
易知∠AOB的终边与单位圆的交点P
O
y
x
A
B
P
M
坐标为 ,所以
求 的正弦,余弦和正切值。
O
y
x
B
A
P
解:在直角坐标系中,作∠AOB=
易知∠AOB的终边与单位圆的交点坐
标为 ,所以
练习:
例2: 已知角α的终边经过点P0(-3,-4),求角α的正弦,余弦和正切值。
解:由已知可得:
设角α的终边与单位圆交于点P(x,y)
分别过点P, P0 作x轴的垂线MP,M0P0
于是,
O
y
x
P0(-3,-4)
M0
P(x,y)
M
则 |M0P0|=4,|OM0|=3,|MP|=-y,|OM|=-x,
△OMP∽△OM0P0,
设α是一个任意角,它的终边上任意一点P(x,y),
点P与原点的距离
那么:(1) 叫做α的正弦,记作sinα,即
sin α=
(2) 叫做α的余弦,记作cosα,即
cos α=
(3) 叫做α的正切, 记作tanα,即
tan α= (x≠0)
定义二:
探究:
三角函数 定义域
sinα
cosα
tanα
R
R
sinα
cosα
tanα
+
+
_
_
_
_
_
_
+
+
+
+
小结:
1、任意角三角函数的定义;
2、三角函数的定义域和函数值在各象限的符号(一全,二正,三切,四余).
作业:
P15 练习 1.2.3
