第四节 角的比较
图片预览






文档简介
(共24张PPT)
前提测评
一.角的定义
二.角的四种表示方法
具有公共端点的两条射线组成的平面图形叫做角.
B
A
C
教学目标
4.4 角的比较
1.进一步丰富对角的认识
2.学会用正确的方法进行角的比较
3.认识角平分线,会画一个角的平分线
4. 角平分线定义的简单应用
锐角:900>α>00
钝角:1800> α>900
周角>平角>钝角>直角>锐角
1平角=1800
1直角=900
1周角=3600
新知探索
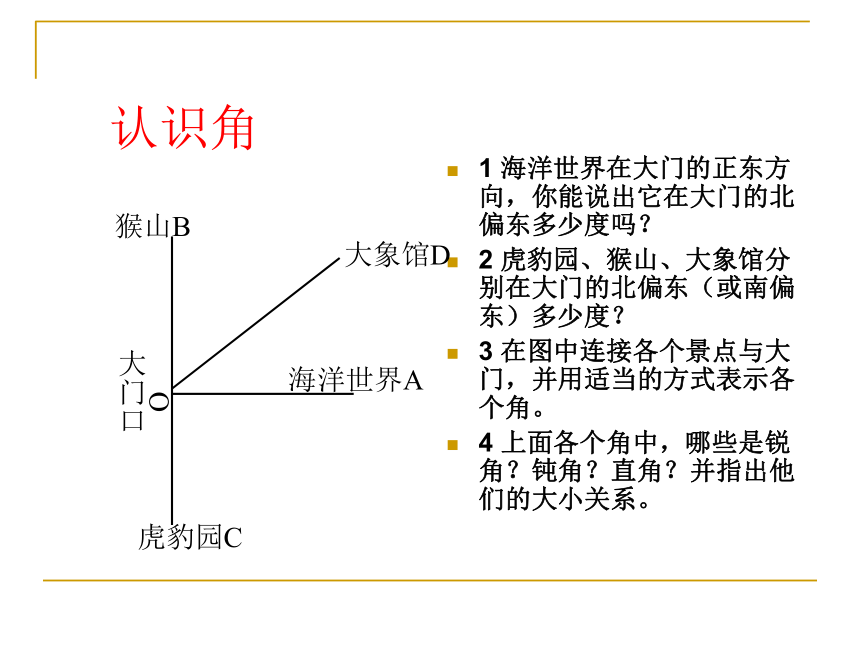
认识角
1 海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?
2 虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东)多少度?
3 在图中连接各个景点与大门,并用适当的方式表示各个角。
4 上面各个角中,哪些是锐角?钝角?直角?并指出他们的大小关系。
猴山B
大象馆D
海洋世界A
虎豹园C
O
大门口
回顾:比较两条线段的长短方法?
1、度量法:用刻度尺测量线段的长度的方法。
2、重叠法:将其中一条线段移到另一条线段上作比较。
问题:比较两个角的大小方法?
A
O
B
C
O
D
G
O
H
E
O
F
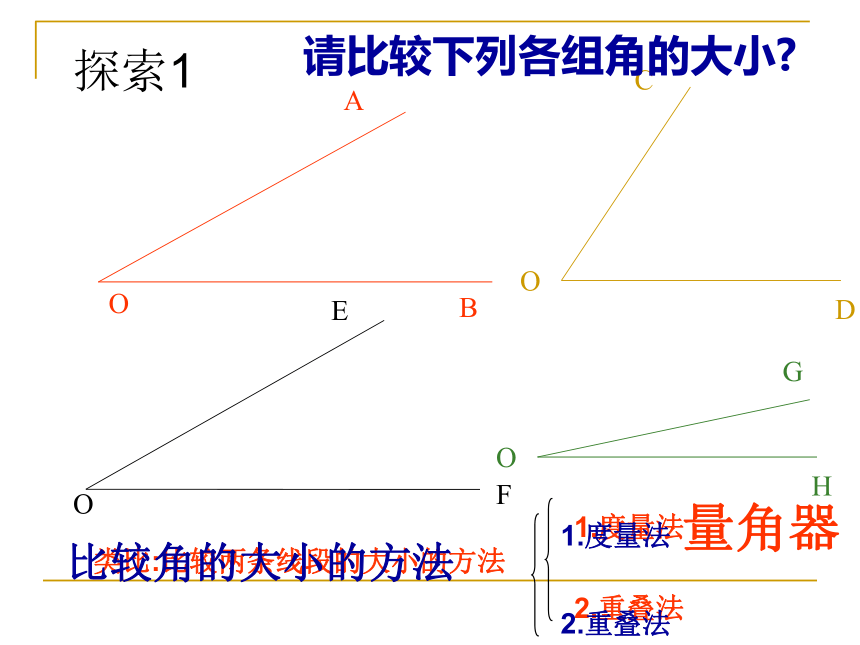
请比较下列各组角的大小
类比:比较两条线段的大小的方法
1.度量法
2.重叠法
比较角的大小的方法
1.度量法
2.重叠法
量角器
探索1
A
O
B
G
O
H
E
O
F
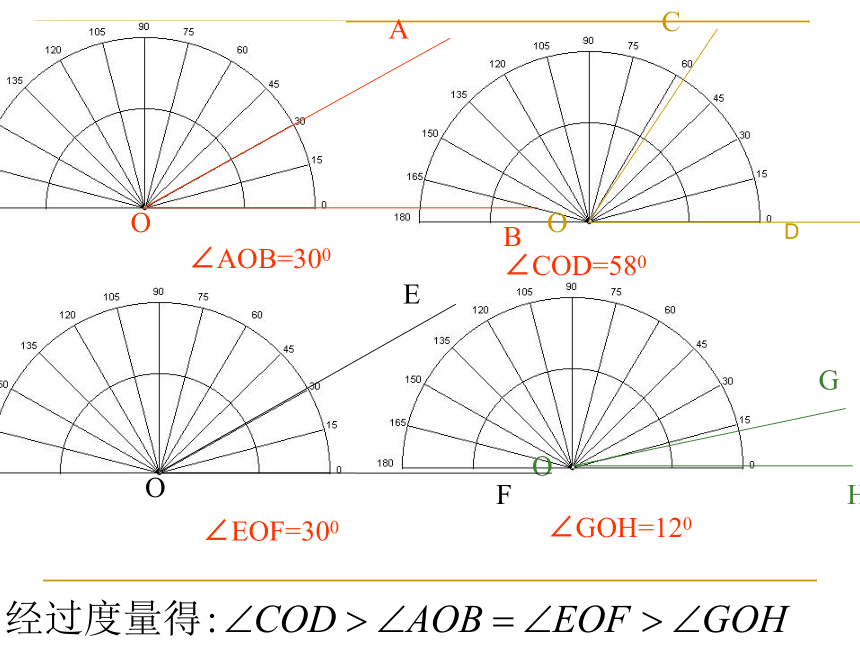
∠AOB=300
∠COD=580
∠EOF=300
∠GOH=120
C
O
D
D
A
O
B
C
O
D
G
O
H
E
O
F
∠AOB< ∠COD
A
O
B
A
O
B
A
O
B
∠AOB= ∠EOF
∠AOB> ∠GOH
2.重叠法
A
O
B
“内小外大”
1 回答下列问题
(1)比较 的大小,
并指出其中的锐角、直角、钝角、平角
(2)写出 中
某些角之间的两个等量关系
∠AOB,
∠AOC,
∠AOE
∠AOD,
∠AOB
,∠AOC
∠AOD
∠AOE
O
A
E
C
D
B
课堂检测
2、如图3.4-2,图中共有几个角?它们之间有什么关系?最大的角是哪个角
C
O
A
B
图3.4-2
折一折
在纸上画一个角并剪下,将它对折使其两边重合,折痕与角两边所成的两个角的大小关系怎样?
探索2
从一个角的顶点引出的一条射线,把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
⌒
2
⌒
⌒
3
1
O
A
C
B
∵∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
C
O
A
B
D
∠AOB
∠BOC
∠COB
∠COD
∠AOB
∠BOC
∠COD
∠COB
∠BOD
练习:1、看图填空:
(1)∠AOC= +
(2) ∠BOD= +
(3) ∠AOD= + +
(4) ∠AOB= ∠AOC = ∠AOD
达标检测
=
>
=
A
B
C
D
2、如图所示: ∠A=700, ∠B=700, ∠ DCB=1400,用“=”或“>”、“<”填空:
(1) ∠ B ∠A
(2) ∠DCB ∠B
(3) ∠ DCB ∠A+ ∠B
∠2
∠ABC
C
B
A
D
1
2
∠ABC
平分线
3、如图:(1)如果BD是∠ABC的角平分线,那么
∠1= =
(2)如果∠ABC=2 ∠2,那么BD是 的
4、如图:OC、OD分别是∠AOB 、∠BOE的平分线,
(1)如果∠AOB=700, ∠BOE=600,那么∠1+ ∠2=
--------
(2) 如果∠1+ ∠2 =550,则∠AOE= --------
A
O
B
C
E
D
1
2
650
1100
90o
O
A
B
D
C
E
5、如图,点O在直线AB上,OD、OE分别是∠AOC 、∠BOC的平分线,则 ∠EOD=
如图3.4-3,借助三角尺画150、750的角。用一副三角尺,你还能画哪些度数的角?试一试!
D
O
C
∠ABC=750
∠DOC=150
如图3.4-3
A
B
C
450
300
E
∠AEC=1350
趣味三角板
拓展
A
B
C
A
C
O
∠ABC=1050
∠AOC=1200
∠EFG=1500
E
G
F
以同桌为单位,你组合角我回答大小.
趣味三角板
本节课有什么收获
1.比较角的大小的方法
1.度量法
2.重叠法
2.角平分线的定义和运用
作业布置:
一.教材151页
问题解决
第1题.
前提测评
一.角的定义
二.角的四种表示方法
具有公共端点的两条射线组成的平面图形叫做角.
B
A
C
教学目标
4.4 角的比较
1.进一步丰富对角的认识
2.学会用正确的方法进行角的比较
3.认识角平分线,会画一个角的平分线
4. 角平分线定义的简单应用
锐角:900>α>00
钝角:1800> α>900
周角>平角>钝角>直角>锐角
1平角=1800
1直角=900
1周角=3600
新知探索
认识角
1 海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?
2 虎豹园、猴山、大象馆分别在大门的北偏东(或南偏东)多少度?
3 在图中连接各个景点与大门,并用适当的方式表示各个角。
4 上面各个角中,哪些是锐角?钝角?直角?并指出他们的大小关系。
猴山B
大象馆D
海洋世界A
虎豹园C
O
大门口
回顾:比较两条线段的长短方法?
1、度量法:用刻度尺测量线段的长度的方法。
2、重叠法:将其中一条线段移到另一条线段上作比较。
问题:比较两个角的大小方法?
A
O
B
C
O
D
G
O
H
E
O
F
请比较下列各组角的大小
类比:比较两条线段的大小的方法
1.度量法
2.重叠法
比较角的大小的方法
1.度量法
2.重叠法
量角器
探索1
A
O
B
G
O
H
E
O
F
∠AOB=300
∠COD=580
∠EOF=300
∠GOH=120
C
O
D
D
A
O
B
C
O
D
G
O
H
E
O
F
∠AOB< ∠COD
A
O
B
A
O
B
A
O
B
∠AOB= ∠EOF
∠AOB> ∠GOH
2.重叠法
A
O
B
“内小外大”
1 回答下列问题
(1)比较 的大小,
并指出其中的锐角、直角、钝角、平角
(2)写出 中
某些角之间的两个等量关系
∠AOB,
∠AOC,
∠AOE
∠AOD,
∠AOB
,∠AOC
∠AOD
∠AOE
O
A
E
C
D
B
课堂检测
2、如图3.4-2,图中共有几个角?它们之间有什么关系?最大的角是哪个角
C
O
A
B
图3.4-2
折一折
在纸上画一个角并剪下,将它对折使其两边重合,折痕与角两边所成的两个角的大小关系怎样?
探索2
从一个角的顶点引出的一条射线,把一个角分成两个相等的角,则这条射线叫这个角的角平分线。
⌒
2
⌒
⌒
3
1
O
A
C
B
∵∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
∴射线OC平分∠AOB
∵射线OC平分∠AOB
∴∠1=∠3 (或∠2= 2∠1 , ∠2= 2∠3)
C
O
A
B
D
∠AOB
∠BOC
∠COB
∠COD
∠AOB
∠BOC
∠COD
∠COB
∠BOD
练习:1、看图填空:
(1)∠AOC= +
(2) ∠BOD= +
(3) ∠AOD= + +
(4) ∠AOB= ∠AOC = ∠AOD
达标检测
=
>
=
A
B
C
D
2、如图所示: ∠A=700, ∠B=700, ∠ DCB=1400,用“=”或“>”、“<”填空:
(1) ∠ B ∠A
(2) ∠DCB ∠B
(3) ∠ DCB ∠A+ ∠B
∠2
∠ABC
C
B
A
D
1
2
∠ABC
平分线
3、如图:(1)如果BD是∠ABC的角平分线,那么
∠1= =
(2)如果∠ABC=2 ∠2,那么BD是 的
4、如图:OC、OD分别是∠AOB 、∠BOE的平分线,
(1)如果∠AOB=700, ∠BOE=600,那么∠1+ ∠2=
--------
(2) 如果∠1+ ∠2 =550,则∠AOE= --------
A
O
B
C
E
D
1
2
650
1100
90o
O
A
B
D
C
E
5、如图,点O在直线AB上,OD、OE分别是∠AOC 、∠BOC的平分线,则 ∠EOD=
如图3.4-3,借助三角尺画150、750的角。用一副三角尺,你还能画哪些度数的角?试一试!
D
O
C
∠ABC=750
∠DOC=150
如图3.4-3
A
B
C
450
300
E
∠AEC=1350
趣味三角板
拓展
A
B
C
A
C
O
∠ABC=1050
∠AOC=1200
∠EFG=1500
E
G
F
以同桌为单位,你组合角我回答大小.
趣味三角板
本节课有什么收获
1.比较角的大小的方法
1.度量法
2.重叠法
2.角平分线的定义和运用
作业布置:
一.教材151页
问题解决
第1题.
