2020-2021学年苏教版数学六下第四单元《比例》期中章节复习精编讲义(含解析)
文档属性
| 名称 | 2020-2021学年苏教版数学六下第四单元《比例》期中章节复习精编讲义(含解析) | 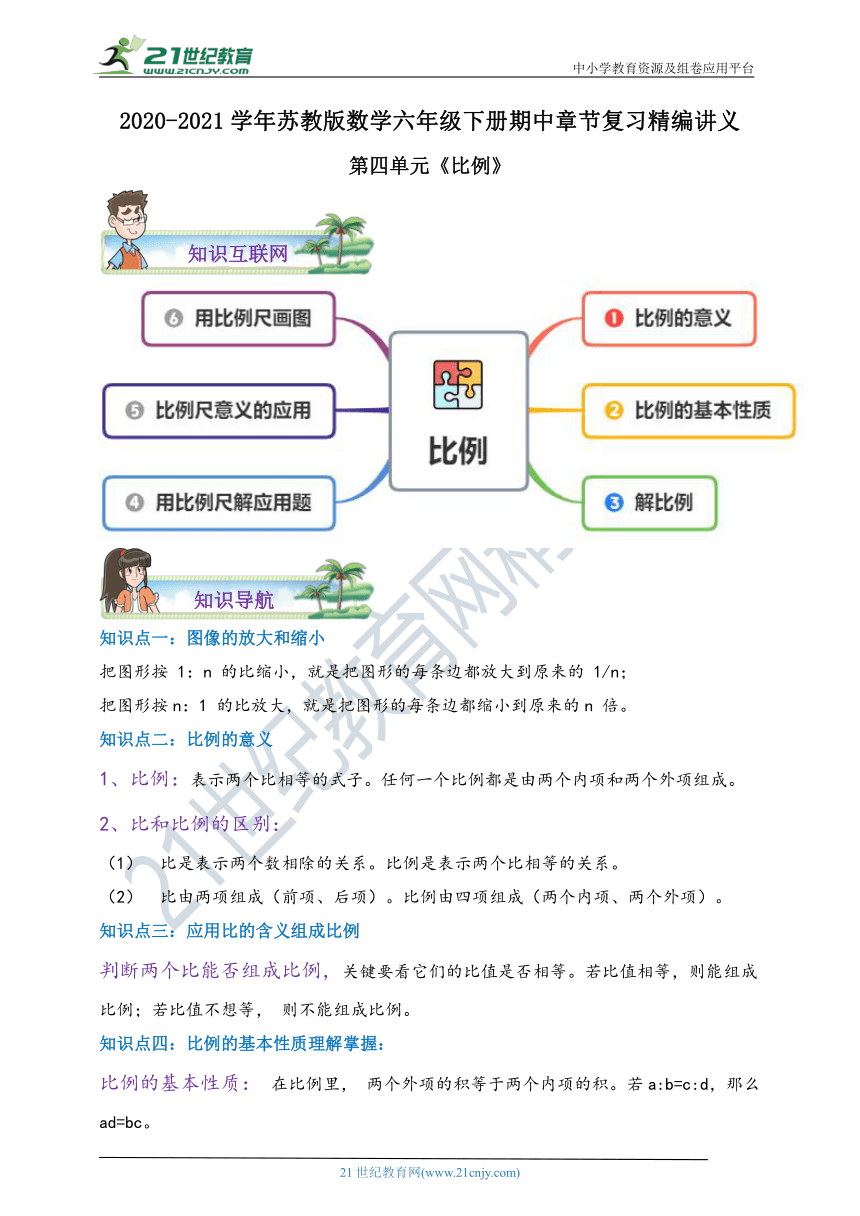 | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 08:56:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年苏教版数学六年级下册期中章节复习精编讲义
第四单元《比例》
知识点一:图像的放大和缩小
把图形按
1:n
的比缩小,就是把图形的每条边都放大到原来的
1/n;
把图形按n:1
的比放大,就是把图形的每条边都缩小到原来的n
倍。
知识点二:比例的意义
1、比例:表示两个比相等的式子。任何一个比例都是由两个内项和两个外项组成。
2、比和比例的区别:
(1)
比是表示两个数相除的关系。比例是表示两个比相等的关系。
(2)
比由两项组成(前项、后项)。比例由四项组成(两个内项、两个外项)。
知识点三:应用比的含义组成比例
判断两个比能否组成比例,关键要看它们的比值是否相等。若比值相等,则能组成比例;若比值不想等,
则不能组成比例。
知识点四:比例的基本性质理解掌握:
比例的基本性质:
在比例里,
两个外项的积等于两个内项的积。若a:b=c:d,那么ad=bc。
若用分数表示比a/b=c/d,那么ad=bc。
十字交叉法
知识点五:解比例
解比例的依据是比例的基本性质,已知比例中的任意三项,就可以求出另外一项。
知识点六:用比例解应用题
解题方法:审题列出比例等量关系式------设未知数列出比例方程
解比例,并检验写答
知识点七:比例尺的意义
比例尺就是图上距离与实际距离的比。
图上距离是比的前项,实际距离是比的后项,比例尺是一个最简单的整数比。
相关公式:(1)比例尺=图上距离÷实际距离
(2)
图上距离=比例尺×实际距离
(3)
实际距离=图上距离÷比例尺
知识点八:比例尺的应用
(1)
注意比例尺的前后单位是否统一。一般比例尺的单位是厘米,而题目往往会给出以千米做单位的比例
尺。如
1:40
千米=1:4000000
厘米
(2)
因为图上距离是比例的前项,实际距离是比例的后项,所以当比例尺的图上距离大于实际距离时,表示设计图纸大于实际物体,如比例尺是
10:1(经常在精密仪器、化学领域中出现);当比例尺的图上距离小于实际距离时,表示设计图纸小于实际物体,如比例尺
1:100(比如设计一栋教学楼)。
一、精挑细选(共5题;每题1分,共5分)
1.(2020·滕州)下面的说法正确的是(???
)。
A.?一个比例的两个外项互为倒数,则两个内项的乘积为1
B.?图上距离总比实际距离小
C.?两个相关联的量,不成正比例就成反比例
2.(2020·临朐)(????
)不能与
:
组成比例式。
A.?3:4???B.?4:3?????C.?1.5:2?????????D.?
:1
3.(2020·浑南)在比例尺是1:10000000地图上,图上距离为10厘米的两地,实际距离是(???
)千米。
A.?10??????B.?100???????C.?1000
4.在比例尺是1:16的图纸上,甲、乙两个圆的半径比是3:5,那么这两个圆的实际面积比是(??
)。
A.?3:5??????B.?1:16??????C.?48:80????D.?9:25
5.在分数
的分子和分母上,同时加上一个相同的整数得到的新分数是
,所加的这个整数是(??
)
A.?2?????B.?4?????C.?5????????D.?7
二、判断正误(共5题;每题1分,共5分)
6.(2020·迁安)一个比例里,两个外项的积是1,则两个内项互为倒数。(
???)
7.(2020·农安)
:
和4:5能组成比例.
8.(2020六下·沿滩月考)甲数的
等于乙数的
,那么甲乙两数的比是8:9。(??
)
9.(2019六下·泗洪期中)如果甲数的
等于乙数的
,那么甲数:乙数=8:15.(??
)
10.比的前项和后项同时增加或减少相同的倍数,比值不变。
三、仔细想,认真填(共9题;每空1分,共21分)
11.(2021六上·自贡期末)在比例尺1:6000000的图上量得东村与西村的距离是12厘米,小军开车从东村出发,每小时行80千米,经过________小时可到达西村.
12.(2020六上·成都月考)某线段比例尺用1厘米表示0.05毫米,用数值比例尺表示为________。
13.(2020·临朐)如果甲数的
等于乙数的
(甲乙都不等于0),那么甲数与乙数的最简比是________。
14.(2020·沈河)如果3a=5b,a、b都不为0,a:b写成最简整数比是________,比值是________。
15.(2020·官渡)在1:300000的地图上量得A、B两城市的距离为20厘米,则这两个城市的实际距离是________千米。
16.
(2019六上·薛城期末)如图表示的数量关系是________;
根据图意,a:b=________:________;
如果已知b=360,那么a=________.
17.
(2019六下·江宁月考)36的约数有________个,从中选择4个数组成比例,这个比例是________;如果使两个比的比值是1
,这个比例是________.
18.已知甲、乙两数的比是
,乙、丙两数的比是
,甲数与丙数的比是________
19.
填一填
(1)3∶4=________∶16=24∶________=________:8=________%
(2)20÷________=________%=0.8=________∶20
四、巧妙作图(共2题;共11分)
20.
(
6分
)
(2020·景县)下图是学校附近的平面图,请你按要求画图。
(1)科技馆在学校的东偏南30°方向500米处,请你在图上标出科技馆的位置。
(2)学园路经过教育局与工业路垂直,请用直线在图中标出学园路的位置。
21.
(
5分
)
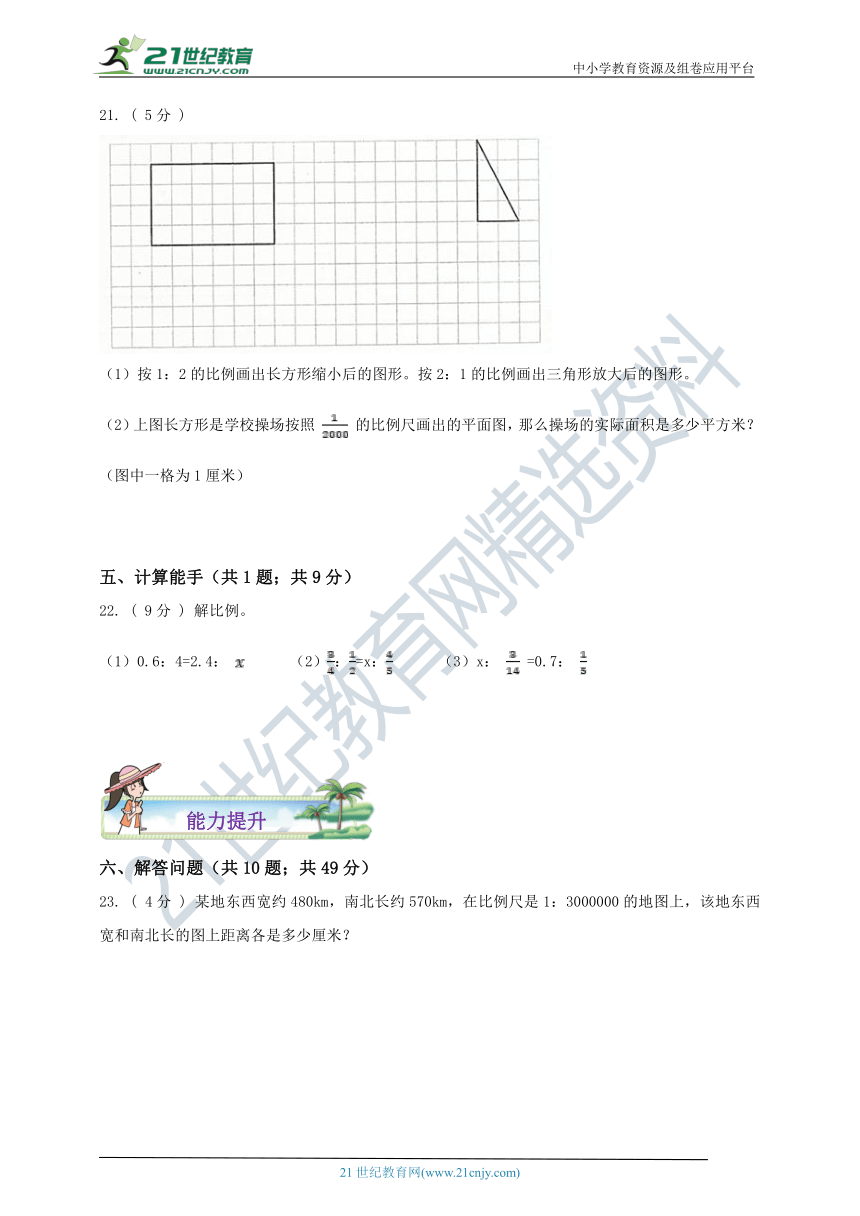
(1)按1:2的比例画出长方形缩小后的图形。按2:1的比例画出三角形放大后的图形。
(2)上图长方形是学校操场按照
的比例尺画出的平面图,那么操场的实际面积是多少平方米?(图中一格为1厘米)
五、计算能手(共1题;共9分)
22.
(
9分
)
解比例。
(1)0.6:4=2.4:
(2):=x:
(3)x:
=0.7:
六、解答问题(共10题;共49分)
23.
(
4分
)
某地东西宽约480km,南北长约570km,在比例尺是1:3000000的地图上,该地东西宽和南北长的图上距离各是多少厘米?
24.
(
4分
)
公园内有一块长240m、宽90m的长方形绿地。请你选择合适的比例尺,算出长方形绿地在图上的长与宽,并画出它的平面图。
我选择的比例尺是(??
)。
①1:1500
?????②1:3000??
???③1:6000
25.
(
5分
)
下面是明明画的一幅简易地图,但是他忘了在图上标出比例尺了。已知明明家到车站的实际距离是600m,到商店的实际距离是400m,到学校的实际距离是200m。请你量一量,算一算,然后在图上标出这幅地图的线段比例尺。
26.
(
5分
)
(2020·东城)在一幅比例尺是1:2000000地图上,量得北京到武汉的距离是60cm,北京到武汉的实际距离是多少千米?
27.
(
5分
)
(2020·东昌府)
(1)学校到医院的图上距离是________厘米,已知实际距离是300米,这幅地图的比例尺是________。
(2)书店到学校的图上距离是________厘米,实际距离是________米。
(3)商场在学校西偏北45°方向,200米处,请在图上标出商场的位置。
28.
(
5分
)
在标有
干米的地图上,量得甲、乙两地的距离为9厘米。如果一辆汽车以每小时60千米的速度从甲地到乙地,需要多少小时?
29.
(
5分
)
(2018六下·深圳月考)在比例尺是1:6000000的地图上,A、B两地间的距离是16厘米。
①A、B两地间的实际距离是多少千米?
②一列火车由A到B用了3小时,火车每小时行多少千米?
30.
(
5分
)
(2020·滕州)在比例尺是1:20000000的地图上量得甲、乙两地间的铁路长6厘米。两列高速列车分别从甲、乙两地同时相对开出,已知从甲地开出的列车平均每小时行315千米,从乙地开出的列车平均每小时行285千米,几小时后两车能相遇?
31.
(
6分
)
(2020·衢州)下图中A、B、C表示三个城市的车站位置。根据图中的比例尺,求下列问题。
(1)先测量图上有关长度(精确到整厘米),再分别求出A站到B站、B站到C站的实际距离。
(2)甲、乙两车分别同时从A、C两站开出,甲车从A到B再到C要行5小时;乙车从C到B再到A要行4小时。照这样的速度,
①两车开出几小时后可以在途中相遇?
②在相遇前当乙车到达B站时,甲车还离B站多少千米?
③如果两车要在B站相遇,则乙车可以从C站迟开出多少小时?
32.
(
5分
)
在标有比例尺
的地图上,量得两地间相距12厘米,一列客车和一列货车从两地同时相向而行,4小时相遇,已知客车与货车的速度比是3:2,客车每小时行驶多少千米.
一、精挑细选
1.
A
解:A:一个比例的两个外项互为倒数,说明两个外项之积是1,那么两个内项的乘积也为1,正确;
B:图上距离不一定比实际距离小,说法错误;
C:两个相关联的量,可能成正比例,也可能成反比例,也可能什么也不成,说法错误。
故答案为:A。
思路引导:A:比例外项之积等于比例内项之积;
B:一般情况下是图上距离小于实际距离,如果是特别精密细小的零件,这时图上距离大于实际距离;
C:积一定,成反比例;商一定,成正比例;其余的不成比例。
2.
B
解:A项:3×=1,4×=1,可以组成比例。
B项:4×=
,
3×=
,
不能组成比例。
C项:1.5×=0.5,2×=0.5,可以组成比例。
D项:×=
,
1×=
,
可以组成比例。
故答案为:B。
思路引导:在比例里,两个内项积等于两个外项积。
3.
C
10÷=100000000(厘米)=1000(千米)
故答案为:C。
思路引导:已知图上距离和比例尺,要求实际距离,图上距离÷比例尺=实际距离,据此计算,然后把厘米化成千米,除以进率100000,据此解答。
4.
D
解:这两个圆的实际面积比32:52=9:25。
故答案为:D。
思路引导:在任何比例尺的图纸上,圆的面积之比等于半径的平方之比。
5.
B
解:设所加的这个数是x,
?
2(5+x)=3(2+x)
10+2x=6+3x
?3x-2x=10-6
????
??
x=4
故答案为:B
思路引导:此题用比例的方法解答比较容易理解,设所加的这个数是x,根据两个分数的分数值不变列出比例,根据比例的基本性质解比例即可求出所加的数.
二、判断正误
6.
正确
两个外项的积是1,那么两个内项的积也是1,乘积为1的两个数互为倒数,所以两个内项互为倒数正确。
故答案为:正确。
思路引导:根据比例的基本性质:两外项之积等于两内项之积,可以知道两个内项的积也是1,再根据倒数的定义:乘积是1的两个数互为倒数进行判断。
7.
错误
解:
:=
÷
=
,4:5=4÷5=
,
因为
,所以
:
和4:5不能组成比例。
故答案为:错误。
思路引导:组成比例的两个比的比值要相等,据此作答即可。
8.
错误
甲数×=乙数×
,
所以甲数:乙数=:
=(×12):(×12)
=9∶8。
故答案为:错误。
思路引导:本题先根据题意列出等式,再根据比例的基本性质(在比例里,两个外项的积等于两个内项的积。)写出甲数∶乙数,最后根据比的基本性质(比的前项和后项同时乘或除以同一个不为0的数比值不变)化成最简整数比即可。
9.
正确
如果甲数×=乙数×
,
则甲数:乙数=:=(×20):(×20)=8:15,原题说法正确.
故答案为:正确.
思路引导:根据条件“
甲数的等于乙数的”可得:甲数×=乙数×
,
依据比例的基本性质,在比例里,两外项之积等于两内项之积,如果甲是一个外项,则是另一个外项,如果乙是一个内项,则是另一个内项,据此写出比,然后化简比即可.
10.
正确
5:6=(2×5):(2×6),所以原说法正确
故答案为:正确
思路引导:比的前项与后项同时增加相同的倍数时,可以将两项增加的倍数同时约除,所以比值的结果不变。同理,当前后两项同时减小相同的倍数时,比值也不变。
三、仔细想,认真填
11.
9
解:实际距离=12÷(1:6000000)
=12×6000000
=72000000(厘米)
=720千米
720÷80=9(小时)
所以经过9小时可到达西村。
故答案为:9。
思路引导:从东村到西村的距离=图上距离÷比例尺,再利用1千米=100000厘米将实际距离的单位转化成千米数,最后利用经过的时间=实际距离(千米数)÷每小时行驶的千米数,代入数值计算即可。
12.
200:1
1厘米=10毫米,10:0.05=200:1。
故答案为:200:1。
思路引导:计算比例尺时,要先统一单位,再根据比例尺=图上距离:实际距离解答即可。
13.
3:4
解:甲:乙=:
甲:乙=(×12):(×12)
甲:乙=3:4
故答案为:3:4。
思路引导:由甲×=乙×可知,甲:乙=:
,
根据比的基本性质,化简比即可。
14.
5:3;
a:b=5:3,比值是5÷3=.
故答案为:5:3;。
思路引导:根据比例的基本性质:两外项之积等于两内项之积,a作外项,那么和a相乘的3也应该作外项,b作内项,和b相乘的5也应该做内项。比值=比的前项÷比的后项。
15.
60
解:20÷=6000000(厘米)=60(千米)。
故答案为:60。
思路引导:用图上距离除以比例尺即可求出实际距离,然后换算单位,1千米=100000厘米。
16.
b=a×(1+);5;6;300
解:数量关系是:b=a×(1+),
根据题意可得a:b=5:6;
如果b=360,所以a=360÷(1+)
=360÷
=300。
故答案为:b=a×(1+);5:6;300。
思路引导:根据图形可得数量关系是b=a×(1+);根据图形可得将a平均分成5份,b比a多其中的1份,即a占5份,b占6份;再将b=360代入算式中,即可得出a的值。
17.
9;4:2=6:3;4:3=12:9
36的约数有1、2、3、4、6、9、12、18、36,共9个;
因为4:2=2,6:3=2,所以这个比例是4:2=6:3;
因为4:3=
,
12:9=
,
所以这个比例是4:3=12:9.
故答案为:9;4:2=6:3;4:3=12:9.
思路引导:比值相等的两个比可以组成比例;比的前项除以比的后项,得出的数就是比值。
18.
2:3
甲数与乙数的比是:=(×5):(×5)=2:4;
乙数与丙数的比是:=(×6):(×6)=4:3;
甲数与丙数的比是2:3.
故答案为:2:3
思路引导:根据题意可知,先将分数比化成整数比,比的前项和后项同时乘分母的最小公倍数,如果还不是最简比,再同时除以相同的数变为最简比;因为乙数在这里是一个过渡量,所以将乙数化成相同的,即可解答.
19.
(1)12;32;6;75
(2)25;80;16
思路引导::比,除法算,百分之间的关系去完成。比的前项相当于除法中的被除数,分数中的分子比的后项相当于除法中的除数,分数中的分母比号相当于除法中的除号,分数中的分数线比值相当于除法中的商,分数的分数值。
四、巧妙作图
20.
(1)解:500米=50000厘米,50000×=2.5(厘米),
如图:
(2)解:
思路引导:(1)把实际距离换算成厘米,用实际距离乘比例尺求出图上距离,然后根据图上的方向、夹角的度数和图上距离确定科技馆的位置;
(2)过教育局作工业路的垂线就是学园路的位置。
21.
(1)
(2)解:画图如下:
6×2000=12000(厘米)=120(米)
4×2000=8000(厘米)=80(米)
120×80=9600(平方米)
答:操场的实际面积是9600平方米。
思路引导:(1)此题主要考查了图形的缩放,先分别数出原图的各边占的格数,然后求出按比例放大或缩小后,各边占的格数,然后作图即可;
(2)此题主要考查了比例尺的应用,已知图上距离与比例尺,可以求出实际距离,图上距离÷比例尺=实际距离,然后用公式:长方形的面积=长×宽,据此列式解答。
五、计算能手
22.
(1)?
?
0.6:4=2.4:x
?解:0.6x=4×2.4
??
????
0.6x=9.6
?0.6x÷0.6=9.6÷0.6
????????????
x=16
(2)?
:=x:
解:x=×
??????
x=
?x÷=÷
?????????
x=
(3)?x:=0.7:
解:x=×0.7
??
???
x=0.15
?x÷=0.15÷
?????????
x=0.75
思路引导:解比例的依据是比例的基本性质:在比例里,两外项之积等于两内项之积,据此解答。
六、解答问题
23.
解:480km=48000000cm
48000000×=16(cm)
570km=57000000cm;
57000000×=19(cm)
答:该地东西宽和南北长的图上距离各是16cm、19cm。
思路引导:图上距离=实际距离×比例尺。
24.
解:根据长方形绿地的长、宽的实际长度,选择1:3000的比例尺比较合适;
3000厘米=30米;
240÷30=8(厘米);
90÷30=3(厘米);
长方形如图所示:
答:我选择的比例尺是②。
思路引导:如果选择1:1500的比例尺,平面图太大;选择1:6000的比例尺,平面图太小;所以选择1:3000的比例尺比较合适;图上距离:实际距离=比例尺,分别计算出长方形的长与宽,从而画出长方形。
25.
解:可以量出明明家到车站在图上的距离是3cm,明明家到商店在图上的距离是2cm,明明家到学校在图上的距离是1cm,
所以比例尺=3:(600×100)=3:60000=1:20000。
如图所示:
思路引导:本题先用直尺测量出明明家到车站、商店以及学校的图上距离,再根据比例尺=图上距离:实际距离,注意将单位统一,即可求出比例尺,再将数值比例尺转化成线段比例尺即可。
26.
解:60÷=120000000(厘米)=1200(千米)
答:北京到武汉的实际距离是1200千米。
思路引导:实际距离=图上距离÷比例尺,然后进行单位换算,即1千米=100000厘米。
27.
(1)3;1:10000
(2)2;200
(3)解:
(1)
学校到医院的图上距离是3厘米,已知实际距离是300米,这幅地图的比例尺是3厘米:300米=3厘米:30000厘米=1:10000;
(2)
书店到学校的图上距离是2厘米,实际距离是200米。
思路引导:(1)用直尺测量物体长度时,要把直尺的0刻度线对准物体的左端,再看物体的末端对着刻度几,就是几厘米,据此测量即可;要求比例尺,图上距离:实际距离=比例尺,据此计算;
(2)根据上述方法,测量出书店到学校的图上距离,要求实际距离,图上距离:比例尺=实际距离,据此解答;
(3)实际距离×比例尺=图上距离,先求出商场在学校西偏北45°方向,图上距离是多少,再作图。
28.
解:9×40=360(千米)?
360÷60=6(时)
9×40=360(千米);
360÷60=6(时).
答:需要6小时.
思路引导:观察线段比例尺可知,图上距离1厘米表示实际距离40千米,图上距离9厘米就相当于实际距离9个40千米,据此列式计算出甲、乙两地之间的路程,然后用路程÷速度=时间,据此列式解答.
29.
解:①16÷=96000000(厘米),96000000厘米=960千米
答:A、B两地间的实际距离是960千米.
②960÷3=320(千米)
答:火车每小时行320千米.
思路引导:①用图上距离除以比例尺即可求出实际距离,注意统一单位;②用实际距离除以时间即可求出每小时行驶的路程.
30.
解:6÷
=6×20000000
=120000000(厘米)
=1200(千米)
1200÷(315+285)
=1200÷600
=2(小时)
答:2小时后两车能相遇。
思路引导:实际距离=图上距离÷比例尺,据此求出实际距离;实际距离÷(甲车速度+乙车速度)=相遇时间。
31.
(1)A站到B站的图上距离是3厘米,B站到C站的图上距离是2厘米。
3÷=15000000(厘米)=150(千米)
2÷=10000000(厘米)=100(千米)
答:A站到B站的实际距离是150千米,B站到C站的实际距离是100千米。
(2)解:甲车速度:250÷5=50(千米)
乙车速度:250÷4=62.5(千米)
①250÷(50+62.5)=250÷112.5=(时)
答:两车开出小时后可以在途中相遇。
②100÷62.5=1.6(时)
150-50×1.6=70(千米)
答:甲车还离B站70千米。
③150÷50=3(小时)
(62.5×3-100)÷62.5=1.4(小时)
答:乙车可以从C站迟开出1.4小时。
思路引导:(1)实际距离=图上距离÷比例尺,然后进行单位换算,即1千米=100000厘米;
(2)甲车的速度=从A到B再到C的距离÷甲车从A到B再到C要行的时间,乙车的速度=从A到B再到C的距离÷乙车从C到B再到A要行的时间;
①两车相遇需要的时间=从A到B再到C的距离÷两车的速度和;
②当乙车到达B站用的时间=从C到B的距离÷乙车的速度,所以甲车还离B站的距离=从A到B的距离-甲车的速度×当乙车到达B站用的时间;
③甲车到达B站用的时间=从A到B的距离÷甲车的速度,那么乙车可以从C站迟开出的时间=(乙车的速度×甲车到达B站用的时间-从C到B的距离)÷乙车的速度。
32.
解:由线段比例尺可知1厘米代表40千米,
两地的路程:40×12=480(千米),
速度和:480÷4=120(千米),
客车速度:120×
=72(千米),
答:客车每小时行驶72千米.
思路引导:由线段比例尺可知1厘米代表40千米,量得两地间相距12厘米,也就是12个40千米,用乘法求出两地的路程,进而根据“路程÷相遇时间=速度之和”求出客车和货车的速度之和;又已知客车和货车速度的比3:2,由此利用按比例分配求得客车的速度,即可解答问题.此题主要考察利用线段比例尺求出实际距离的方法,再根据路程、相遇时间和速度之和三者之间的关系及按比例分配知识进行解答.
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年苏教版数学六年级下册期中章节复习精编讲义
第四单元《比例》
知识点一:图像的放大和缩小
把图形按
1:n
的比缩小,就是把图形的每条边都放大到原来的
1/n;
把图形按n:1
的比放大,就是把图形的每条边都缩小到原来的n
倍。
知识点二:比例的意义
1、比例:表示两个比相等的式子。任何一个比例都是由两个内项和两个外项组成。
2、比和比例的区别:
(1)
比是表示两个数相除的关系。比例是表示两个比相等的关系。
(2)
比由两项组成(前项、后项)。比例由四项组成(两个内项、两个外项)。
知识点三:应用比的含义组成比例
判断两个比能否组成比例,关键要看它们的比值是否相等。若比值相等,则能组成比例;若比值不想等,
则不能组成比例。
知识点四:比例的基本性质理解掌握:
比例的基本性质:
在比例里,
两个外项的积等于两个内项的积。若a:b=c:d,那么ad=bc。
若用分数表示比a/b=c/d,那么ad=bc。
十字交叉法
知识点五:解比例
解比例的依据是比例的基本性质,已知比例中的任意三项,就可以求出另外一项。
知识点六:用比例解应用题
解题方法:审题列出比例等量关系式------设未知数列出比例方程
解比例,并检验写答
知识点七:比例尺的意义
比例尺就是图上距离与实际距离的比。
图上距离是比的前项,实际距离是比的后项,比例尺是一个最简单的整数比。
相关公式:(1)比例尺=图上距离÷实际距离
(2)
图上距离=比例尺×实际距离
(3)
实际距离=图上距离÷比例尺
知识点八:比例尺的应用
(1)
注意比例尺的前后单位是否统一。一般比例尺的单位是厘米,而题目往往会给出以千米做单位的比例
尺。如
1:40
千米=1:4000000
厘米
(2)
因为图上距离是比例的前项,实际距离是比例的后项,所以当比例尺的图上距离大于实际距离时,表示设计图纸大于实际物体,如比例尺是
10:1(经常在精密仪器、化学领域中出现);当比例尺的图上距离小于实际距离时,表示设计图纸小于实际物体,如比例尺
1:100(比如设计一栋教学楼)。
一、精挑细选(共5题;每题1分,共5分)
1.(2020·滕州)下面的说法正确的是(???
)。
A.?一个比例的两个外项互为倒数,则两个内项的乘积为1
B.?图上距离总比实际距离小
C.?两个相关联的量,不成正比例就成反比例
2.(2020·临朐)(????
)不能与
:
组成比例式。
A.?3:4???B.?4:3?????C.?1.5:2?????????D.?
:1
3.(2020·浑南)在比例尺是1:10000000地图上,图上距离为10厘米的两地,实际距离是(???
)千米。
A.?10??????B.?100???????C.?1000
4.在比例尺是1:16的图纸上,甲、乙两个圆的半径比是3:5,那么这两个圆的实际面积比是(??
)。
A.?3:5??????B.?1:16??????C.?48:80????D.?9:25
5.在分数
的分子和分母上,同时加上一个相同的整数得到的新分数是
,所加的这个整数是(??
)
A.?2?????B.?4?????C.?5????????D.?7
二、判断正误(共5题;每题1分,共5分)
6.(2020·迁安)一个比例里,两个外项的积是1,则两个内项互为倒数。(
???)
7.(2020·农安)
:
和4:5能组成比例.
8.(2020六下·沿滩月考)甲数的
等于乙数的
,那么甲乙两数的比是8:9。(??
)
9.(2019六下·泗洪期中)如果甲数的
等于乙数的
,那么甲数:乙数=8:15.(??
)
10.比的前项和后项同时增加或减少相同的倍数,比值不变。
三、仔细想,认真填(共9题;每空1分,共21分)
11.(2021六上·自贡期末)在比例尺1:6000000的图上量得东村与西村的距离是12厘米,小军开车从东村出发,每小时行80千米,经过________小时可到达西村.
12.(2020六上·成都月考)某线段比例尺用1厘米表示0.05毫米,用数值比例尺表示为________。
13.(2020·临朐)如果甲数的
等于乙数的
(甲乙都不等于0),那么甲数与乙数的最简比是________。
14.(2020·沈河)如果3a=5b,a、b都不为0,a:b写成最简整数比是________,比值是________。
15.(2020·官渡)在1:300000的地图上量得A、B两城市的距离为20厘米,则这两个城市的实际距离是________千米。
16.
(2019六上·薛城期末)如图表示的数量关系是________;
根据图意,a:b=________:________;
如果已知b=360,那么a=________.
17.
(2019六下·江宁月考)36的约数有________个,从中选择4个数组成比例,这个比例是________;如果使两个比的比值是1
,这个比例是________.
18.已知甲、乙两数的比是
,乙、丙两数的比是
,甲数与丙数的比是________
19.
填一填
(1)3∶4=________∶16=24∶________=________:8=________%
(2)20÷________=________%=0.8=________∶20
四、巧妙作图(共2题;共11分)
20.
(
6分
)
(2020·景县)下图是学校附近的平面图,请你按要求画图。
(1)科技馆在学校的东偏南30°方向500米处,请你在图上标出科技馆的位置。
(2)学园路经过教育局与工业路垂直,请用直线在图中标出学园路的位置。
21.
(
5分
)
(1)按1:2的比例画出长方形缩小后的图形。按2:1的比例画出三角形放大后的图形。
(2)上图长方形是学校操场按照
的比例尺画出的平面图,那么操场的实际面积是多少平方米?(图中一格为1厘米)
五、计算能手(共1题;共9分)
22.
(
9分
)
解比例。
(1)0.6:4=2.4:
(2):=x:
(3)x:
=0.7:
六、解答问题(共10题;共49分)
23.
(
4分
)
某地东西宽约480km,南北长约570km,在比例尺是1:3000000的地图上,该地东西宽和南北长的图上距离各是多少厘米?
24.
(
4分
)
公园内有一块长240m、宽90m的长方形绿地。请你选择合适的比例尺,算出长方形绿地在图上的长与宽,并画出它的平面图。
我选择的比例尺是(??
)。
①1:1500
?????②1:3000??
???③1:6000
25.
(
5分
)
下面是明明画的一幅简易地图,但是他忘了在图上标出比例尺了。已知明明家到车站的实际距离是600m,到商店的实际距离是400m,到学校的实际距离是200m。请你量一量,算一算,然后在图上标出这幅地图的线段比例尺。
26.
(
5分
)
(2020·东城)在一幅比例尺是1:2000000地图上,量得北京到武汉的距离是60cm,北京到武汉的实际距离是多少千米?
27.
(
5分
)
(2020·东昌府)
(1)学校到医院的图上距离是________厘米,已知实际距离是300米,这幅地图的比例尺是________。
(2)书店到学校的图上距离是________厘米,实际距离是________米。
(3)商场在学校西偏北45°方向,200米处,请在图上标出商场的位置。
28.
(
5分
)
在标有
干米的地图上,量得甲、乙两地的距离为9厘米。如果一辆汽车以每小时60千米的速度从甲地到乙地,需要多少小时?
29.
(
5分
)
(2018六下·深圳月考)在比例尺是1:6000000的地图上,A、B两地间的距离是16厘米。
①A、B两地间的实际距离是多少千米?
②一列火车由A到B用了3小时,火车每小时行多少千米?
30.
(
5分
)
(2020·滕州)在比例尺是1:20000000的地图上量得甲、乙两地间的铁路长6厘米。两列高速列车分别从甲、乙两地同时相对开出,已知从甲地开出的列车平均每小时行315千米,从乙地开出的列车平均每小时行285千米,几小时后两车能相遇?
31.
(
6分
)
(2020·衢州)下图中A、B、C表示三个城市的车站位置。根据图中的比例尺,求下列问题。
(1)先测量图上有关长度(精确到整厘米),再分别求出A站到B站、B站到C站的实际距离。
(2)甲、乙两车分别同时从A、C两站开出,甲车从A到B再到C要行5小时;乙车从C到B再到A要行4小时。照这样的速度,
①两车开出几小时后可以在途中相遇?
②在相遇前当乙车到达B站时,甲车还离B站多少千米?
③如果两车要在B站相遇,则乙车可以从C站迟开出多少小时?
32.
(
5分
)
在标有比例尺
的地图上,量得两地间相距12厘米,一列客车和一列货车从两地同时相向而行,4小时相遇,已知客车与货车的速度比是3:2,客车每小时行驶多少千米.
一、精挑细选
1.
A
解:A:一个比例的两个外项互为倒数,说明两个外项之积是1,那么两个内项的乘积也为1,正确;
B:图上距离不一定比实际距离小,说法错误;
C:两个相关联的量,可能成正比例,也可能成反比例,也可能什么也不成,说法错误。
故答案为:A。
思路引导:A:比例外项之积等于比例内项之积;
B:一般情况下是图上距离小于实际距离,如果是特别精密细小的零件,这时图上距离大于实际距离;
C:积一定,成反比例;商一定,成正比例;其余的不成比例。
2.
B
解:A项:3×=1,4×=1,可以组成比例。
B项:4×=
,
3×=
,
不能组成比例。
C项:1.5×=0.5,2×=0.5,可以组成比例。
D项:×=
,
1×=
,
可以组成比例。
故答案为:B。
思路引导:在比例里,两个内项积等于两个外项积。
3.
C
10÷=100000000(厘米)=1000(千米)
故答案为:C。
思路引导:已知图上距离和比例尺,要求实际距离,图上距离÷比例尺=实际距离,据此计算,然后把厘米化成千米,除以进率100000,据此解答。
4.
D
解:这两个圆的实际面积比32:52=9:25。
故答案为:D。
思路引导:在任何比例尺的图纸上,圆的面积之比等于半径的平方之比。
5.
B
解:设所加的这个数是x,
?
2(5+x)=3(2+x)
10+2x=6+3x
?3x-2x=10-6
????
??
x=4
故答案为:B
思路引导:此题用比例的方法解答比较容易理解,设所加的这个数是x,根据两个分数的分数值不变列出比例,根据比例的基本性质解比例即可求出所加的数.
二、判断正误
6.
正确
两个外项的积是1,那么两个内项的积也是1,乘积为1的两个数互为倒数,所以两个内项互为倒数正确。
故答案为:正确。
思路引导:根据比例的基本性质:两外项之积等于两内项之积,可以知道两个内项的积也是1,再根据倒数的定义:乘积是1的两个数互为倒数进行判断。
7.
错误
解:
:=
÷
=
,4:5=4÷5=
,
因为
,所以
:
和4:5不能组成比例。
故答案为:错误。
思路引导:组成比例的两个比的比值要相等,据此作答即可。
8.
错误
甲数×=乙数×
,
所以甲数:乙数=:
=(×12):(×12)
=9∶8。
故答案为:错误。
思路引导:本题先根据题意列出等式,再根据比例的基本性质(在比例里,两个外项的积等于两个内项的积。)写出甲数∶乙数,最后根据比的基本性质(比的前项和后项同时乘或除以同一个不为0的数比值不变)化成最简整数比即可。
9.
正确
如果甲数×=乙数×
,
则甲数:乙数=:=(×20):(×20)=8:15,原题说法正确.
故答案为:正确.
思路引导:根据条件“
甲数的等于乙数的”可得:甲数×=乙数×
,
依据比例的基本性质,在比例里,两外项之积等于两内项之积,如果甲是一个外项,则是另一个外项,如果乙是一个内项,则是另一个内项,据此写出比,然后化简比即可.
10.
正确
5:6=(2×5):(2×6),所以原说法正确
故答案为:正确
思路引导:比的前项与后项同时增加相同的倍数时,可以将两项增加的倍数同时约除,所以比值的结果不变。同理,当前后两项同时减小相同的倍数时,比值也不变。
三、仔细想,认真填
11.
9
解:实际距离=12÷(1:6000000)
=12×6000000
=72000000(厘米)
=720千米
720÷80=9(小时)
所以经过9小时可到达西村。
故答案为:9。
思路引导:从东村到西村的距离=图上距离÷比例尺,再利用1千米=100000厘米将实际距离的单位转化成千米数,最后利用经过的时间=实际距离(千米数)÷每小时行驶的千米数,代入数值计算即可。
12.
200:1
1厘米=10毫米,10:0.05=200:1。
故答案为:200:1。
思路引导:计算比例尺时,要先统一单位,再根据比例尺=图上距离:实际距离解答即可。
13.
3:4
解:甲:乙=:
甲:乙=(×12):(×12)
甲:乙=3:4
故答案为:3:4。
思路引导:由甲×=乙×可知,甲:乙=:
,
根据比的基本性质,化简比即可。
14.
5:3;
a:b=5:3,比值是5÷3=.
故答案为:5:3;。
思路引导:根据比例的基本性质:两外项之积等于两内项之积,a作外项,那么和a相乘的3也应该作外项,b作内项,和b相乘的5也应该做内项。比值=比的前项÷比的后项。
15.
60
解:20÷=6000000(厘米)=60(千米)。
故答案为:60。
思路引导:用图上距离除以比例尺即可求出实际距离,然后换算单位,1千米=100000厘米。
16.
b=a×(1+);5;6;300
解:数量关系是:b=a×(1+),
根据题意可得a:b=5:6;
如果b=360,所以a=360÷(1+)
=360÷
=300。
故答案为:b=a×(1+);5:6;300。
思路引导:根据图形可得数量关系是b=a×(1+);根据图形可得将a平均分成5份,b比a多其中的1份,即a占5份,b占6份;再将b=360代入算式中,即可得出a的值。
17.
9;4:2=6:3;4:3=12:9
36的约数有1、2、3、4、6、9、12、18、36,共9个;
因为4:2=2,6:3=2,所以这个比例是4:2=6:3;
因为4:3=
,
12:9=
,
所以这个比例是4:3=12:9.
故答案为:9;4:2=6:3;4:3=12:9.
思路引导:比值相等的两个比可以组成比例;比的前项除以比的后项,得出的数就是比值。
18.
2:3
甲数与乙数的比是:=(×5):(×5)=2:4;
乙数与丙数的比是:=(×6):(×6)=4:3;
甲数与丙数的比是2:3.
故答案为:2:3
思路引导:根据题意可知,先将分数比化成整数比,比的前项和后项同时乘分母的最小公倍数,如果还不是最简比,再同时除以相同的数变为最简比;因为乙数在这里是一个过渡量,所以将乙数化成相同的,即可解答.
19.
(1)12;32;6;75
(2)25;80;16
思路引导::比,除法算,百分之间的关系去完成。比的前项相当于除法中的被除数,分数中的分子比的后项相当于除法中的除数,分数中的分母比号相当于除法中的除号,分数中的分数线比值相当于除法中的商,分数的分数值。
四、巧妙作图
20.
(1)解:500米=50000厘米,50000×=2.5(厘米),
如图:
(2)解:
思路引导:(1)把实际距离换算成厘米,用实际距离乘比例尺求出图上距离,然后根据图上的方向、夹角的度数和图上距离确定科技馆的位置;
(2)过教育局作工业路的垂线就是学园路的位置。
21.
(1)
(2)解:画图如下:
6×2000=12000(厘米)=120(米)
4×2000=8000(厘米)=80(米)
120×80=9600(平方米)
答:操场的实际面积是9600平方米。
思路引导:(1)此题主要考查了图形的缩放,先分别数出原图的各边占的格数,然后求出按比例放大或缩小后,各边占的格数,然后作图即可;
(2)此题主要考查了比例尺的应用,已知图上距离与比例尺,可以求出实际距离,图上距离÷比例尺=实际距离,然后用公式:长方形的面积=长×宽,据此列式解答。
五、计算能手
22.
(1)?
?
0.6:4=2.4:x
?解:0.6x=4×2.4
??
????
0.6x=9.6
?0.6x÷0.6=9.6÷0.6
????????????
x=16
(2)?
:=x:
解:x=×
??????
x=
?x÷=÷
?????????
x=
(3)?x:=0.7:
解:x=×0.7
??
???
x=0.15
?x÷=0.15÷
?????????
x=0.75
思路引导:解比例的依据是比例的基本性质:在比例里,两外项之积等于两内项之积,据此解答。
六、解答问题
23.
解:480km=48000000cm
48000000×=16(cm)
570km=57000000cm;
57000000×=19(cm)
答:该地东西宽和南北长的图上距离各是16cm、19cm。
思路引导:图上距离=实际距离×比例尺。
24.
解:根据长方形绿地的长、宽的实际长度,选择1:3000的比例尺比较合适;
3000厘米=30米;
240÷30=8(厘米);
90÷30=3(厘米);
长方形如图所示:
答:我选择的比例尺是②。
思路引导:如果选择1:1500的比例尺,平面图太大;选择1:6000的比例尺,平面图太小;所以选择1:3000的比例尺比较合适;图上距离:实际距离=比例尺,分别计算出长方形的长与宽,从而画出长方形。
25.
解:可以量出明明家到车站在图上的距离是3cm,明明家到商店在图上的距离是2cm,明明家到学校在图上的距离是1cm,
所以比例尺=3:(600×100)=3:60000=1:20000。
如图所示:
思路引导:本题先用直尺测量出明明家到车站、商店以及学校的图上距离,再根据比例尺=图上距离:实际距离,注意将单位统一,即可求出比例尺,再将数值比例尺转化成线段比例尺即可。
26.
解:60÷=120000000(厘米)=1200(千米)
答:北京到武汉的实际距离是1200千米。
思路引导:实际距离=图上距离÷比例尺,然后进行单位换算,即1千米=100000厘米。
27.
(1)3;1:10000
(2)2;200
(3)解:
(1)
学校到医院的图上距离是3厘米,已知实际距离是300米,这幅地图的比例尺是3厘米:300米=3厘米:30000厘米=1:10000;
(2)
书店到学校的图上距离是2厘米,实际距离是200米。
思路引导:(1)用直尺测量物体长度时,要把直尺的0刻度线对准物体的左端,再看物体的末端对着刻度几,就是几厘米,据此测量即可;要求比例尺,图上距离:实际距离=比例尺,据此计算;
(2)根据上述方法,测量出书店到学校的图上距离,要求实际距离,图上距离:比例尺=实际距离,据此解答;
(3)实际距离×比例尺=图上距离,先求出商场在学校西偏北45°方向,图上距离是多少,再作图。
28.
解:9×40=360(千米)?
360÷60=6(时)
9×40=360(千米);
360÷60=6(时).
答:需要6小时.
思路引导:观察线段比例尺可知,图上距离1厘米表示实际距离40千米,图上距离9厘米就相当于实际距离9个40千米,据此列式计算出甲、乙两地之间的路程,然后用路程÷速度=时间,据此列式解答.
29.
解:①16÷=96000000(厘米),96000000厘米=960千米
答:A、B两地间的实际距离是960千米.
②960÷3=320(千米)
答:火车每小时行320千米.
思路引导:①用图上距离除以比例尺即可求出实际距离,注意统一单位;②用实际距离除以时间即可求出每小时行驶的路程.
30.
解:6÷
=6×20000000
=120000000(厘米)
=1200(千米)
1200÷(315+285)
=1200÷600
=2(小时)
答:2小时后两车能相遇。
思路引导:实际距离=图上距离÷比例尺,据此求出实际距离;实际距离÷(甲车速度+乙车速度)=相遇时间。
31.
(1)A站到B站的图上距离是3厘米,B站到C站的图上距离是2厘米。
3÷=15000000(厘米)=150(千米)
2÷=10000000(厘米)=100(千米)
答:A站到B站的实际距离是150千米,B站到C站的实际距离是100千米。
(2)解:甲车速度:250÷5=50(千米)
乙车速度:250÷4=62.5(千米)
①250÷(50+62.5)=250÷112.5=(时)
答:两车开出小时后可以在途中相遇。
②100÷62.5=1.6(时)
150-50×1.6=70(千米)
答:甲车还离B站70千米。
③150÷50=3(小时)
(62.5×3-100)÷62.5=1.4(小时)
答:乙车可以从C站迟开出1.4小时。
思路引导:(1)实际距离=图上距离÷比例尺,然后进行单位换算,即1千米=100000厘米;
(2)甲车的速度=从A到B再到C的距离÷甲车从A到B再到C要行的时间,乙车的速度=从A到B再到C的距离÷乙车从C到B再到A要行的时间;
①两车相遇需要的时间=从A到B再到C的距离÷两车的速度和;
②当乙车到达B站用的时间=从C到B的距离÷乙车的速度,所以甲车还离B站的距离=从A到B的距离-甲车的速度×当乙车到达B站用的时间;
③甲车到达B站用的时间=从A到B的距离÷甲车的速度,那么乙车可以从C站迟开出的时间=(乙车的速度×甲车到达B站用的时间-从C到B的距离)÷乙车的速度。
32.
解:由线段比例尺可知1厘米代表40千米,
两地的路程:40×12=480(千米),
速度和:480÷4=120(千米),
客车速度:120×
=72(千米),
答:客车每小时行驶72千米.
思路引导:由线段比例尺可知1厘米代表40千米,量得两地间相距12厘米,也就是12个40千米,用乘法求出两地的路程,进而根据“路程÷相遇时间=速度之和”求出客车和货车的速度之和;又已知客车和货车速度的比3:2,由此利用按比例分配求得客车的速度,即可解答问题.此题主要考察利用线段比例尺求出实际距离的方法,再根据路程、相遇时间和速度之和三者之间的关系及按比例分配知识进行解答.
知识互联网
知识导航
夯实基础
能力提升
能力达标百分训练(答案解析)
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
