勾股定理的应用课件
图片预览





文档简介
(共19张PPT)
练习: 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
3、已知:数3和4,请你再写一个数,使
这些数恰好是一个直角三角形三边长,则这个数可以是( )
4、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是( )
X
X
5
24
勾股定理能解决直角三角形的许多问题,因此在我们的现实生活中有着广泛的应用.如:这些美丽的图案
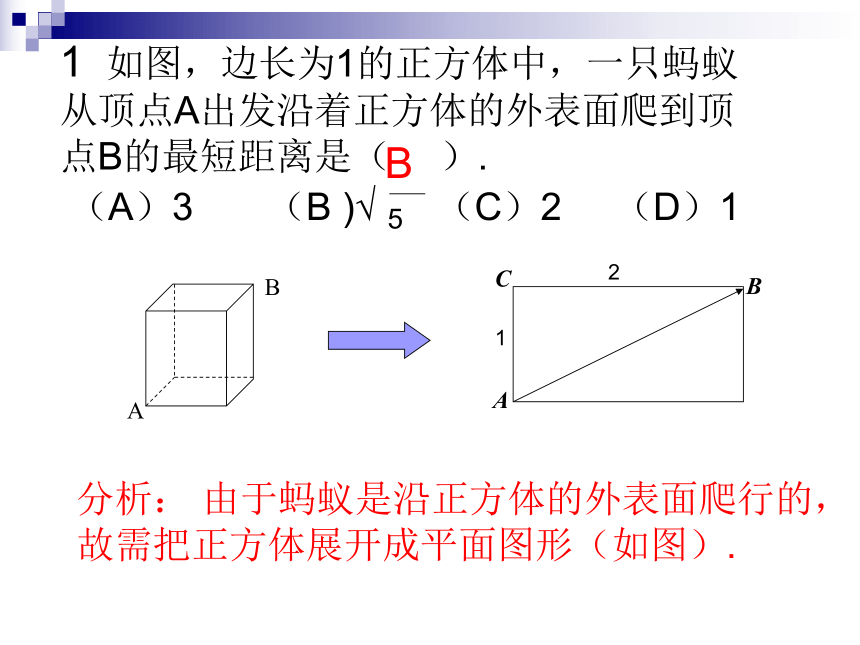
1 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1
A
B
A
B
C
2
1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
台阶中的最值问题
例1 . 如图,是一个三级台阶,它的每一级的长、宽和
高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食
物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B
点,最短线路是多少?
A
B
C
D
解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
A
B
C
D
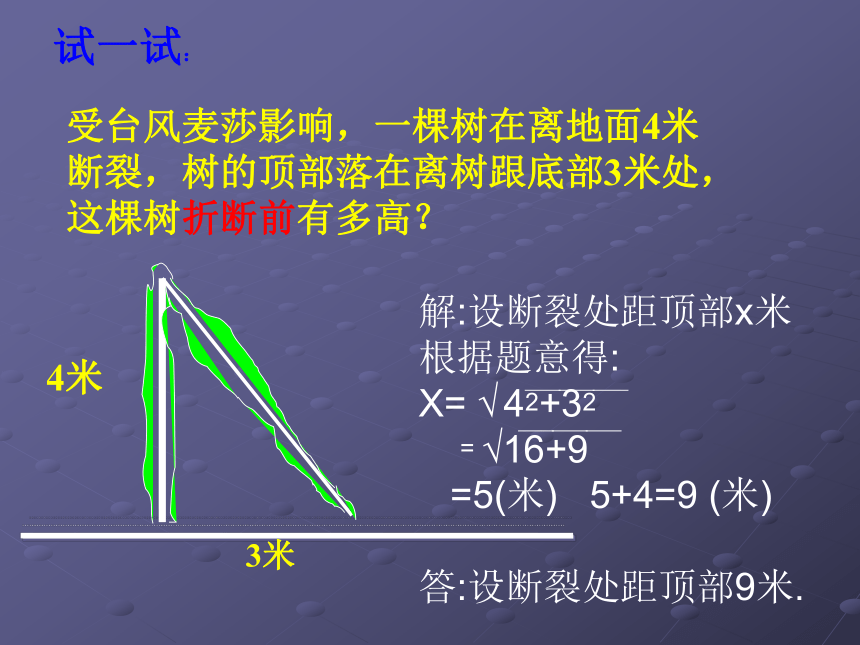
受台风麦莎影响,一棵树在离地面4米
断裂,树的顶部落在离树跟底部3米处,
这棵树折断前有多高?
4米
3米
解:设断裂处距顶部x米
根据题意得:
X= √ 42+32
= √16+9
=5(米) 5+4=9 (米)
答:设断裂处距顶部9米.
试一试:
试一试:
在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
解:设,则水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1
=12+1
=13(米)
答:水池的深度为12米,芦苇高为13米.
y=0
例2、如图:是一个长方形零件图,根据所给的
尺寸,求两孔中心A、B之间的距离
A
B
C
4
9
16
4
解: 如图所示,在直角三
角形ABC中,
AC=9-4 BC=16-4
=5 =12
根据勾股定理可得
AB= √ BC2+AC2
= √122+52
=13
答:两孔中心A、B之间的距离为13
想一想
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电
视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉
得一定是售货员搞错了.你同意他的想法吗?你能解释这是
为什么吗?
通过这节课的学习
活动你有哪些收获?
1 做一个长,宽,高分别为50厘米,40厘米,
30厘米的木箱,一根长为70厘米的木棒能否放
入,为什么?试用今天学过的知识说明。
拓展
2、如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
A
B
D
E
C
3、如图,把长方形纸片ABCD折叠,使顶点A与
顶点C重合在一起,EF为折痕。若AB=9,BC=3,
试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
H
练习: 1. ABC的两边AB=5,AC=12,则BC=13 ( )
2. ABC的a=6,b=8,则c=10 ( )
3、已知:数3和4,请你再写一个数,使
这些数恰好是一个直角三角形三边长,则这个数可以是( )
4、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是( )
X
X
5
24
勾股定理能解决直角三角形的许多问题,因此在我们的现实生活中有着广泛的应用.如:这些美丽的图案
1 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B )√ 5 (C)2 (D)1
A
B
A
B
C
2
1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
小 结:
把几何体适当展开成平面图形,再利用“两点之间线段最短”性质来解决问题。
台阶中的最值问题
例1 . 如图,是一个三级台阶,它的每一级的长、宽和
高分别等于5cm,3cm和1cm,A和B是这个台阶的两个
相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食
物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B
点,最短线路是多少?
A
B
C
D
解: ∵ AB2=AC2+BC2=169,
∴ AB=13.
答:从A点爬到B点,最短线路是13.
A
B
C
D
受台风麦莎影响,一棵树在离地面4米
断裂,树的顶部落在离树跟底部3米处,
这棵树折断前有多高?
4米
3米
解:设断裂处距顶部x米
根据题意得:
X= √ 42+32
= √16+9
=5(米) 5+4=9 (米)
答:设断裂处距顶部9米.
试一试:
试一试:
在我国古代数学著作《九章算术》
中记载了一道有趣的问题,这个问
题意思是:有一个水池,水面是一
个边长为10尺的正方形,在水池的
中央有一根新生的芦苇,它高出水
面1尺,如果把这根芦苇拉向岸边,
它的顶端恰好到达岸边的水面,问
这个水池的深度和这根芦苇的长度
各是多少?
D
A
B
C
解:设,则水池的深度为X米,
芦苇高为 (X+1)米.
根据题意得:
AB2=BC2+AC2
(X+1)2=52+X2
X2+2X+1=25+X2
X=12
X+1
=12+1
=13(米)
答:水池的深度为12米,芦苇高为13米.
y=0
例2、如图:是一个长方形零件图,根据所给的
尺寸,求两孔中心A、B之间的距离
A
B
C
4
9
16
4
解: 如图所示,在直角三
角形ABC中,
AC=9-4 BC=16-4
=5 =12
根据勾股定理可得
AB= √ BC2+AC2
= √122+52
=13
答:两孔中心A、B之间的距离为13
想一想
小明妈妈买了一部29英寸(74厘米)的电视机.小明量了电
视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉
得一定是售货员搞错了.你同意他的想法吗?你能解释这是
为什么吗?
通过这节课的学习
活动你有哪些收获?
1 做一个长,宽,高分别为50厘米,40厘米,
30厘米的木箱,一根长为70厘米的木棒能否放
入,为什么?试用今天学过的知识说明。
拓展
2、如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
A
B
D
E
C
3、如图,把长方形纸片ABCD折叠,使顶点A与
顶点C重合在一起,EF为折痕。若AB=9,BC=3,
试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
H
