平行线的性质课件

(共14张PPT)
第三课时
平行线的性质
平行线的判定方法有哪三种？它
们是先知道什么……、 后知道什么？
同位角相等
内错角相等
同旁内角互补
两直线平行
问题
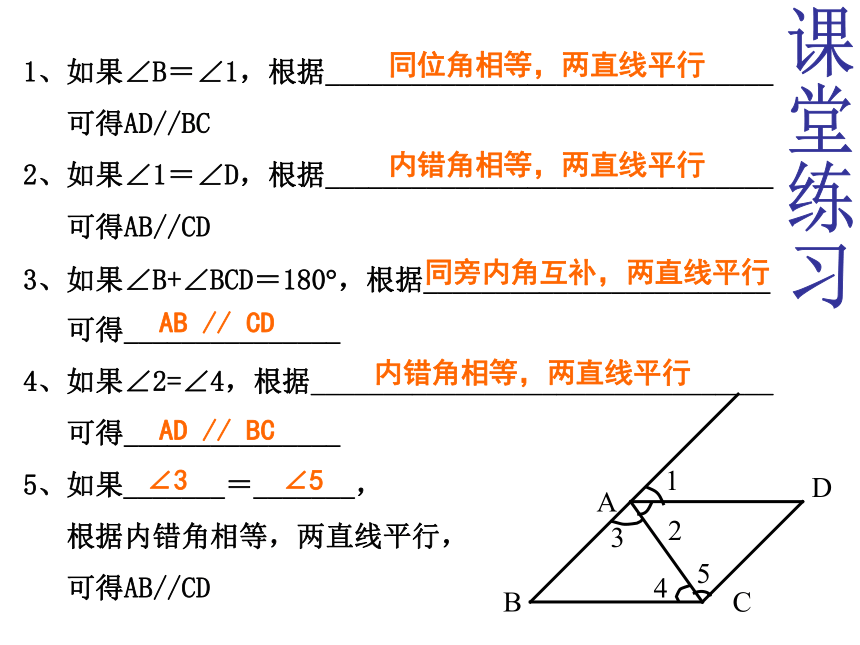
1、如果∠B＝∠1，根据_______________________________
可得AD//BC
2、如果∠1＝∠D，根据_______________________________
可得AB//CD
3、如果∠B+∠BCD＝180 ，根据________________________
可得_______________
4、如果∠2=∠4，根据________________________________
可得_______________
5、如果_______＝_______，
根据内错角相等，两直线平行，
可得AB//CD
A
B
C
D
1
2
3
4
5
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补，两直线平行
AB // CD
内错角相等，两直线平行
AD // BC
∠5
∠3
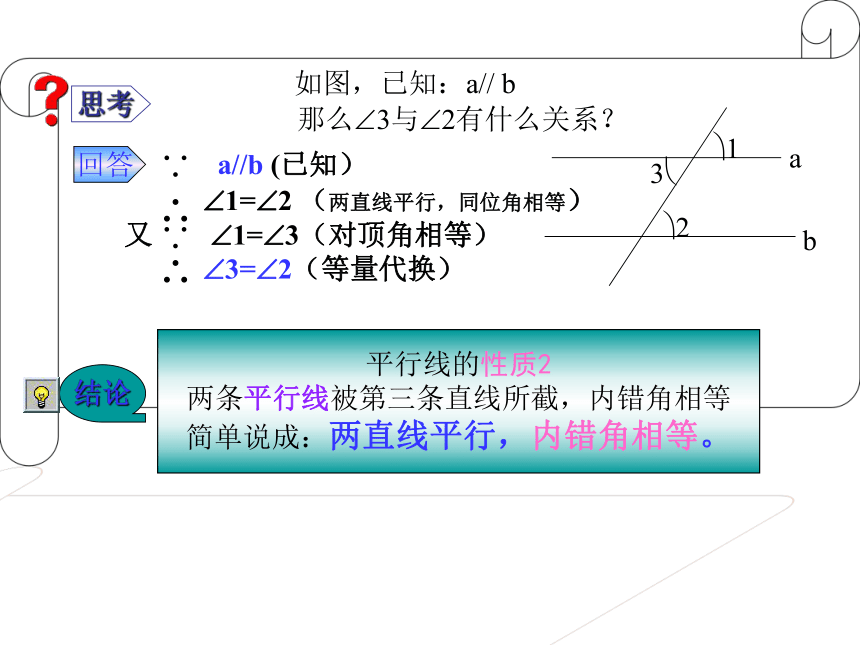
如果两条直线平行，那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系？
平行线的性质1（公理）
两条平行线被第三条直线所截，同位角相等。
简单说成：两直线平行，同位角相等。
问题
结论
性质2
a//b (已知）
1= 2 （两直线平行，同位角相等）
又 1= 3（对顶角相等）
3= 2（等量代换）
1
2
3
a
b
思考
回答




如图，已知：a// b
那么 3与 2有什么关系？
平行线的性质2
两条平行线被第三条直线所截，内错角相等
简单说成：两直线平行，内错角相等。
结论
c

2

3
1
b
a
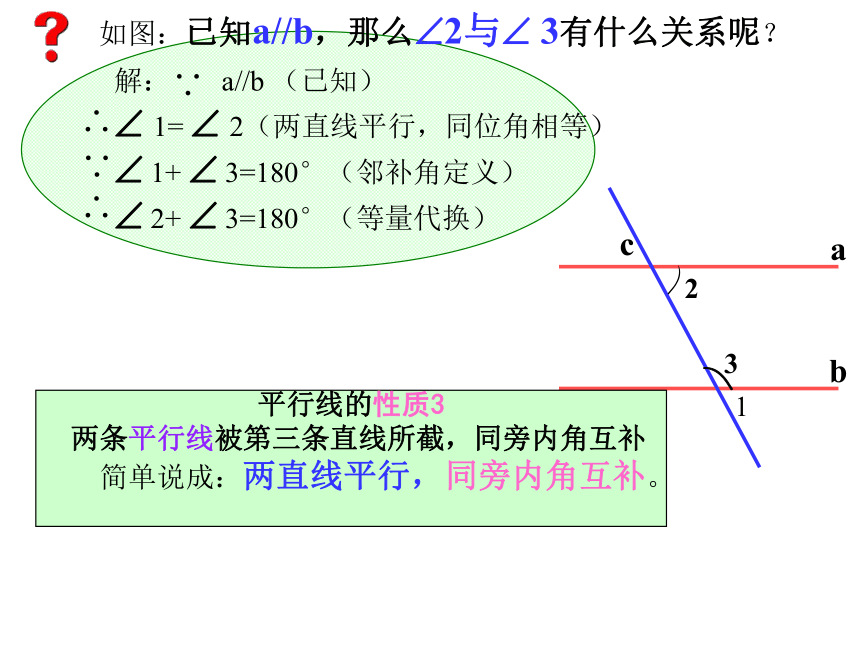
解： a//b （已知）
1= 2（两直线平行，同位角相等）
1+ 3=180°（邻补角定义）
2+ 3=180°（等量代换）
如图：已知a//b，那么 2与 3有什么关系呢？
平行线的性质3
两条平行线被第三条直线所截，同旁内角互补
简单说成：两直线平行，同旁内角互补。




平行线的性质1（公理）
两条平行线被第三条直线所截，同位角相等。
简单说成：两直线平行，同位角相等。
平行线的性质2
两条平行线被第三条直线所截，内错角相等
简单说成：两直线平行，内错角相等。
平行线的性质3
两条平行线被第三条直线所截，同旁内角互补
简单说成：两直线平行，同旁内角互补。
精彩回放
两类定理的比较
两条平行直线被第三条直线直线所截，
同位角相等， 两直线平行
两直线平行，同位角相等。
判定定理
性质定理
条件 结论
条件 结论
思考:
1、判定定理与性质定理的
条件与结论有什么关系？
互换。
内错角相等， 两直线平行
两直线平行，内错角相等。
同旁内角互补，两直线平行
两直线平行，同旁内角互补
2、使用判定定理时是
已知 ，说明 ；
角的相等或互补
两直线平行
使用性质定理时是
已知 ，说明 。
两直线平行
角的相等或互补
平行线的“判定”与“性质”有什么不同
比一比
已知角之间的关系(相等或互补)，得到两直线平行
的结论是平行线的判定。
已知两直线平行，得到角之间的关系(相等或互补)
的结论是平行线的性质。
巩固练习：
1、如果AD//BC，根据__________________________
可得∠B=∠1
2、如果AB//CD，根据___________________________
可得∠D＝∠1
3、如果AD//BC，根据___________________________
可得∠C＋_______＝180
A
B
C
D
1
两直线平行，同位角相等
两直线平行，内错角相等
两直线平行，同旁内角互补
∠D
c
d
a
b
3
4
2
1
例2 如图所示 ∠1 =∠2
求证 ： ∠3 =∠4
证明：∵ ∠1 =∠2（已知）
∴a//b
(同位角相等,两直线平行)
∴ ∠3 =∠4
(两直线平行，内错角相等)
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结1：
复习回顾
新课学习
巩固练习
课堂小结
小结2
判定定理
性质定理
由“线”定“角”
由“线”的位置关系（平行），定“角”的数量关系（相等或互补）
由“角”定“线”
由“角”的数量关系（相等或互补）定“线”的位置关系（平行），