北师大版七年级数学下册《整式的乘法》(第三课时)(共33张ppt)
文档属性
| 名称 | 北师大版七年级数学下册《整式的乘法》(第三课时)(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 417.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 19:20:16 | ||
图片预览







文档简介
回顾与思考
② 再把所得的积相加。
如何进行单项式与多项式乘法的运算?
① 用单项式分别去乘多项式的每一项;
单项式乘以多项式的依据是
;
乘法的分配律.
进行单项式与多项式乘法运算时,要注意一些什么?
① 不能漏乘:
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
回顾与思考
1.4 整式的乘法
第3课时 多项式与多项式相乘
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.
(难点)
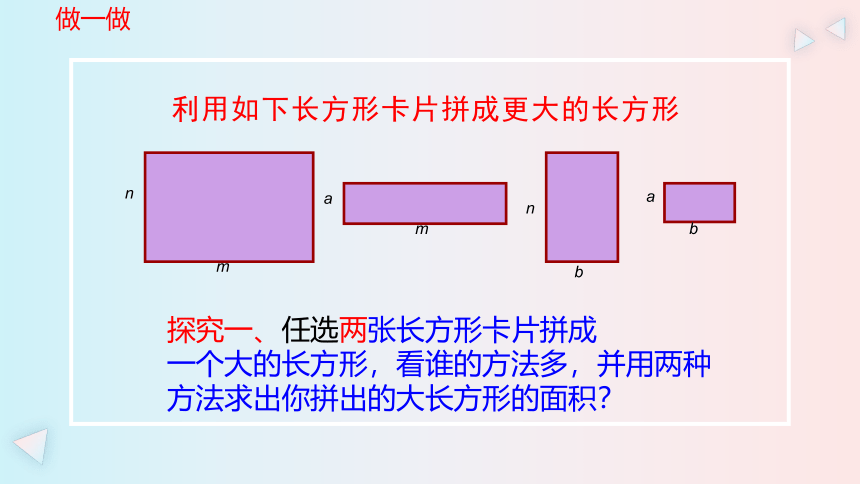
利用如下长方形卡片拼成更大的长方形
m
n
m
a
b
n
b
a
探究一、任选两张长方形卡片拼成
一个大的长方形,看谁的方法多,并用两种方法求出你拼出的大长方形的面积?
做一做
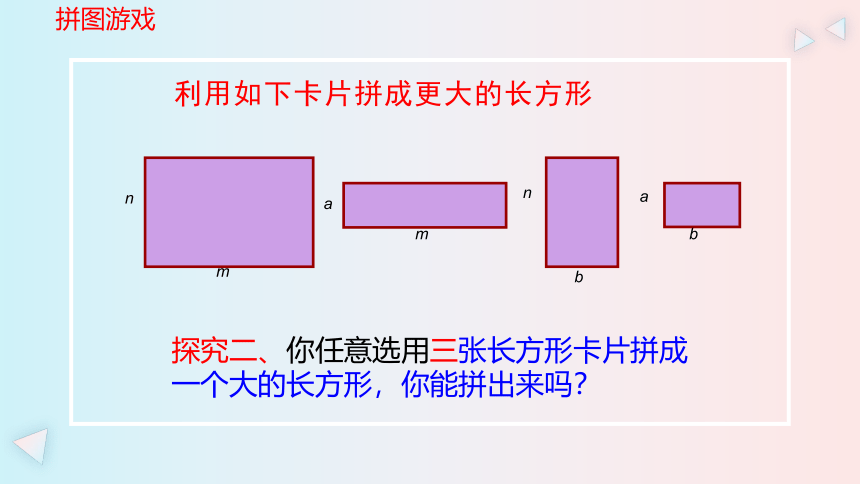
利用如下卡片拼成更大的长方形
m
n
m
a
b
n
b
a
探究二、你任意选用三张长方形卡片拼成一个大的长方形,你能拼出来吗?
拼图游戏
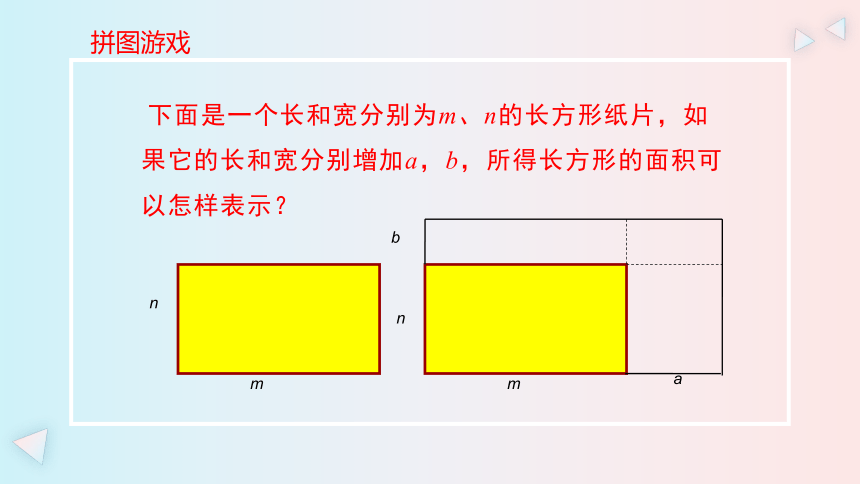
下面是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a,b,所得长方形的面积可以怎样表示?
m
n
n
m
b
a
拼图游戏
长方形的面积可以有4种表示方式:
1.(m+a)(n+b)
2. n(m+a)+b(m+a)
3. m(n+b)+a(n+b)
4. mn+mb+an+ab
我们从中可以看出:
(m+a)(n+b)=n(m+a)+b(m+a)
=m(n+b)+a(n+b)=mn+mb+an+ab
你认为他的想法对吗?从中你受到了什么启发?
把(m+a)或者(n+b) 看成一个整体,利用乘法分配律,用单项式乘多项式法则理解
将等号两端的x换成(n+b)
则有:
在 (m+a) x =mx+ax 中,
(m+a) x =m x +a x
(n+b)
(n+b)
(n+b)
=mn+mb + an+ab
1
2
3
4
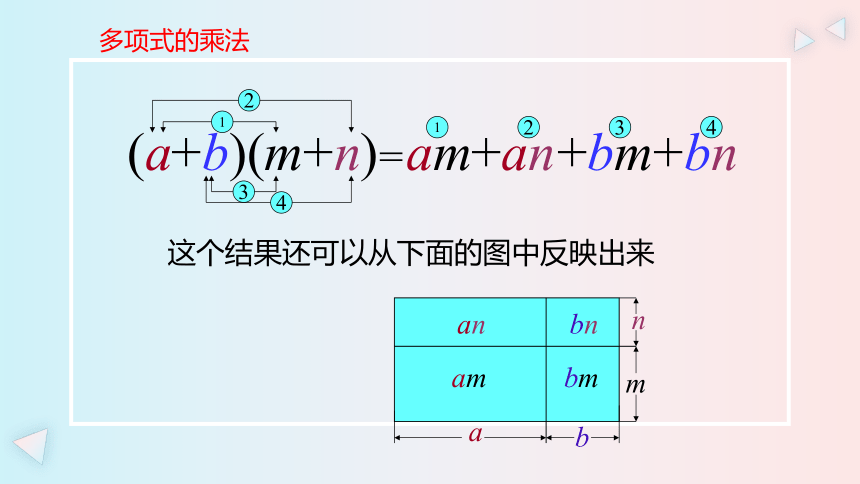
(a+b)(m+n)
=
am
1
2
3
4
这个结果还可以从下面的图中反映出来
a
b
m
n
am
an
bn
bm
+an
+bm
+bn
多项式的乘法
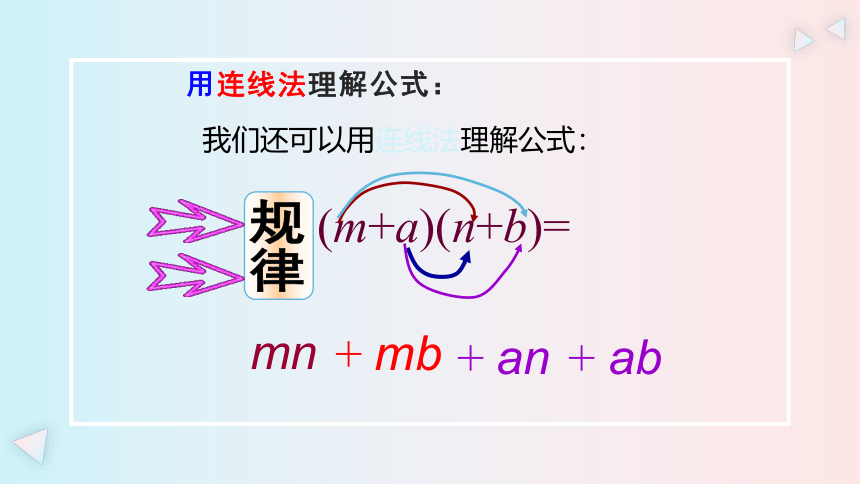
用连线法理解公式:
规律
(m+a)(n+b)=
mn
+ mb
+ ab
+ an
我们还可以用连线法理解公式:
学会连一连:
(a+b)(c+d)=
ac
+bc
+bd
+ad
-乙丁
(甲+乙)(丙–丁)=
甲丙
+乙丙
-甲丁
学会连一连:
(①+②)(①+②)=
①①
+①②
+②①
+②②
学会连一连:
如何记忆多项式与多项式相乘的运算?
多项式与多项式相乘
先用一个多项式的每一项乘另一个多项式的每一项,
再把所得的积相加。
(m+a)(n+b)=
mn
+ mb
+ an
+ ab
多项式乘多项式
问题1 (a+b)X= ?
(a+b)X=aX+bX
(a+b)X=(a+b)(m+n)
当X=m+n时, (a+b)X=?
提出问题
讲授新课
问题2 某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
a
m
b
n
ma
na
mb
nb
a
m
b
n
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb.
(m+n)(a+b)
= (m+n)a+(m+n)b
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
知识要点
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
典例精析
例1 计算:(1)(1-x)(0.6-x);
(2)(2x+y)(x-y);
解: (1) 原式=1×0.6-1×x-x·0.6+x·x
=0.6-x-0.6x+x2
=0.6-1.6x+x2;
(2) 原式=2x·x-2x·y+y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2;
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成
最简形式(是同类项的要合并).
(3) (x+y)(x2-xy+y2).
例2 先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
方法总结:化简求值的题型,一定要注意先化简,
再求值,不能先代值,再计算.
当堂练习
1.判别下列解法是否正确,若错请说出理由.
解:原式
解:原式
2.计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).
= ?x2 +4xy?21y2;
解:(1)原式=x2+7xy?3yx?21y2
(2)原式=2x?3x ?2x? 2y+5 y? 3x?5y?2y
=6x2?4xy+15xy?10y2
=6x2+11xy?10y2.
3.计算求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中
x=1,y=-2.
解:原式=
当x=1,y=-2时,原式=22×12-7×1×(-2)
-14×(-2)2=22+14-56=-20.
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
4.计算:
5.小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?
七年级(下)
姓名:____________
数学
c
b
a
a
b
c
m
b
m
面积:(2m+2b+c)(2m+a)
解:(2m+2b+c)(2m+a)
= 4m2+2ma+4bm+2ab+2cm+ca.
答:小东应在挂历画上裁下一块(4m2+2ma+4bm
+2ab+2cm+ca)平方厘米的长方形.
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12.
② 再把所得的积相加。
如何进行单项式与多项式乘法的运算?
① 用单项式分别去乘多项式的每一项;
单项式乘以多项式的依据是
;
乘法的分配律.
进行单项式与多项式乘法运算时,要注意一些什么?
① 不能漏乘:
即单项式要乘遍多项式的每一项.
② 去括号时注意符号的确定.
回顾与思考
1.4 整式的乘法
第3课时 多项式与多项式相乘
学习目标
1.理解并掌握多项式与多项式的乘法运算法则.(重点)
2.能够用多项式与多项式的乘法运算法则进行计算.
(难点)
利用如下长方形卡片拼成更大的长方形
m
n
m
a
b
n
b
a
探究一、任选两张长方形卡片拼成
一个大的长方形,看谁的方法多,并用两种方法求出你拼出的大长方形的面积?
做一做
利用如下卡片拼成更大的长方形
m
n
m
a
b
n
b
a
探究二、你任意选用三张长方形卡片拼成一个大的长方形,你能拼出来吗?
拼图游戏
下面是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a,b,所得长方形的面积可以怎样表示?
m
n
n
m
b
a
拼图游戏
长方形的面积可以有4种表示方式:
1.(m+a)(n+b)
2. n(m+a)+b(m+a)
3. m(n+b)+a(n+b)
4. mn+mb+an+ab
我们从中可以看出:
(m+a)(n+b)=n(m+a)+b(m+a)
=m(n+b)+a(n+b)=mn+mb+an+ab
你认为他的想法对吗?从中你受到了什么启发?
把(m+a)或者(n+b) 看成一个整体,利用乘法分配律,用单项式乘多项式法则理解
将等号两端的x换成(n+b)
则有:
在 (m+a) x =mx+ax 中,
(m+a) x =m x +a x
(n+b)
(n+b)
(n+b)
=mn+mb + an+ab
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
这个结果还可以从下面的图中反映出来
a
b
m
n
am
an
bn
bm
+an
+bm
+bn
多项式的乘法
用连线法理解公式:
规律
(m+a)(n+b)=
mn
+ mb
+ ab
+ an
我们还可以用连线法理解公式:
学会连一连:
(a+b)(c+d)=
ac
+bc
+bd
+ad
-乙丁
(甲+乙)(丙–丁)=
甲丙
+乙丙
-甲丁
学会连一连:
(①+②)(①+②)=
①①
+①②
+②①
+②②
学会连一连:
如何记忆多项式与多项式相乘的运算?
多项式与多项式相乘
先用一个多项式的每一项乘另一个多项式的每一项,
再把所得的积相加。
(m+a)(n+b)=
mn
+ mb
+ an
+ ab
多项式乘多项式
问题1 (a+b)X= ?
(a+b)X=aX+bX
(a+b)X=(a+b)(m+n)
当X=m+n时, (a+b)X=?
提出问题
讲授新课
问题2 某地区在退耕还林期间,有一块原长m米,宽为a米的长方形林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
a
m
b
n
ma
na
mb
nb
a
m
b
n
你能用不同的形式表示所拼图的面积吗?
这块林区现在长为(m+n)米,宽为(a+b)米.
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb.
如何进行多项式与多项式相乘的运算?
实际上,把(m+n)看成一个整体,有:
= ma+mb+na+nb.
(m+n)(a+b)
= (m+n)a+(m+n)b
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
知识要点
多项式乘以多项式
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多乘多顺口溜:
多乘多,来计算,多项式各项都见面,
乘后结果要相加,化简、排列才算完.
典例精析
例1 计算:(1)(1-x)(0.6-x);
(2)(2x+y)(x-y);
解: (1) 原式=1×0.6-1×x-x·0.6+x·x
=0.6-x-0.6x+x2
=0.6-1.6x+x2;
(2) 原式=2x·x-2x·y+y·x-y·y
=2x2-2xy+xy-y2
=2x2-xy-y2;
解:原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
注意:(1)漏乘;(2)符号问题;(3)最后结果应化成
最简形式(是同类项的要合并).
(3) (x+y)(x2-xy+y2).
例2 先化简,再求值:(a-2b)(a2+2ab+4b2)-a(a-5b)(a+3b),其中a=-1,b=1.
解:原式=a3-8b3-(a2-5ab)(a+3b)
=a3-8b3-a3-3a2b+5a2b+15ab2
=-8b3+2a2b+15ab2.
当a=-1,b=1时,原式=-8+2-15=-21.
方法总结:化简求值的题型,一定要注意先化简,
再求值,不能先代值,再计算.
当堂练习
1.判别下列解法是否正确,若错请说出理由.
解:原式
解:原式
2.计算:(1)(x?3y)(x+7y); (2)(2x + 5y)(3x?2y).
= ?x2 +4xy?21y2;
解:(1)原式=x2+7xy?3yx?21y2
(2)原式=2x?3x ?2x? 2y+5 y? 3x?5y?2y
=6x2?4xy+15xy?10y2
=6x2+11xy?10y2.
3.计算求值:(4x+3y)(4x-3y)+(2x+y)(3x-5y),其中
x=1,y=-2.
解:原式=
当x=1,y=-2时,原式=22×12-7×1×(-2)
-14×(-2)2=22+14-56=-20.
观察上面四个等式,你能发现什么规律?并应用这个规律解决下面的问题.
5 6
(-3) (-4)
2 (-8)
(-5) 6
口答:
4.计算:
5.小东找来一张挂历画包数学课本.已知课本长a厘米,宽b厘米,厚c厘米,小东想将课本封面与封底的每一边都包进去m厘米,问小东应在挂历画上裁下一块多大面积的长方形?
七年级(下)
姓名:____________
数学
c
b
a
a
b
c
m
b
m
面积:(2m+2b+c)(2m+a)
解:(2m+2b+c)(2m+a)
= 4m2+2ma+4bm+2ab+2cm+ca.
答:小东应在挂历画上裁下一块(4m2+2ma+4bm
+2ab+2cm+ca)平方厘米的长方形.
课堂小结
多项式乘多项式
运算法则
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加
(a+b)(m+n)=am+an+bm+bn
注意
不要漏乘;正确确定各项符号;结果要最简
实质上是转化为单项式×多项式的运算
(x-1)2=(x-1)(x-1),而不是x2-12.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
