6.1 圆周运动 教学设计
图片预览

文档简介
圆周运动(节选)
一、任务分解
二、教学活动
任务1:圆周运动及快慢的描述
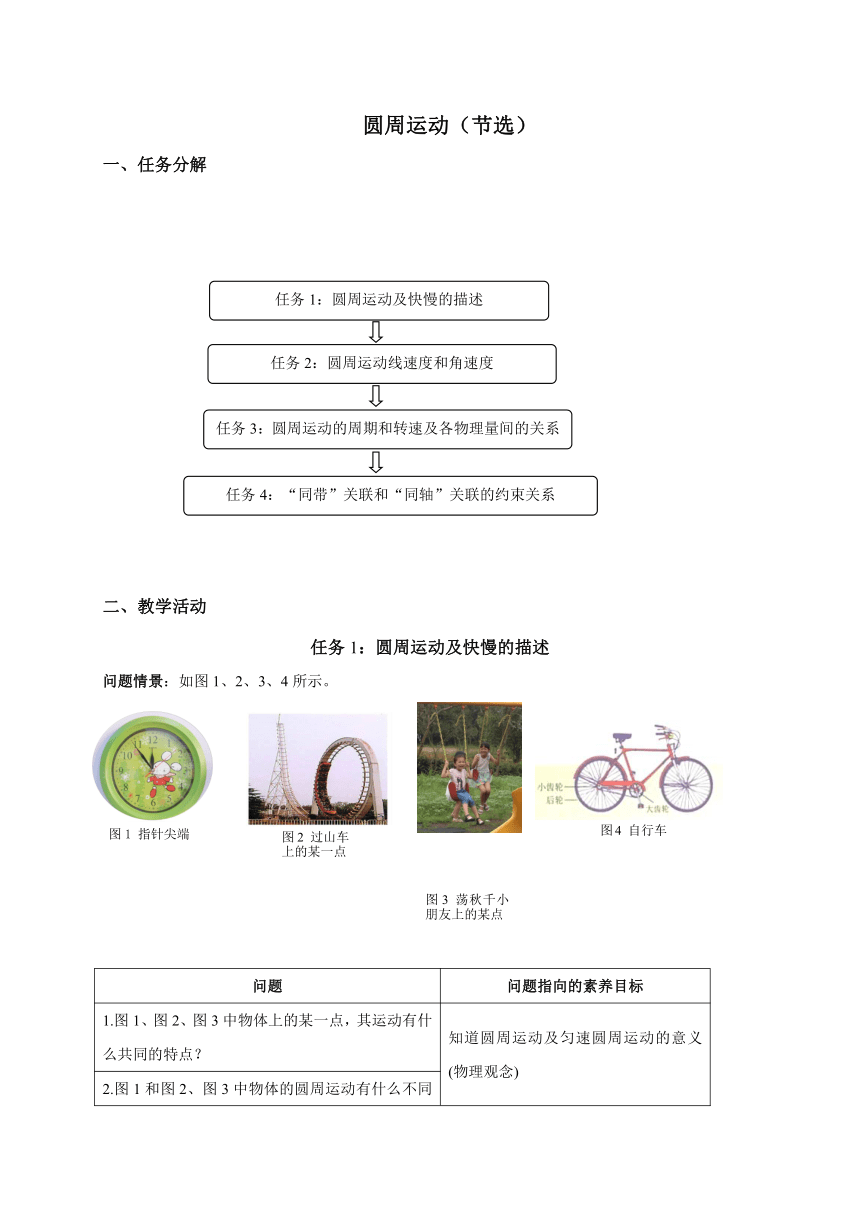
问题情景:如图1、2、3、4所示。
问题 问题指向的素养目标
1.图1、图2、图3中物体上的某一点,其运动有什么共同的特点? 知道圆周运动及匀速圆周运动的意义(物理观念)
2.图1和图2、图3中物体的圆周运动有什么不同之处?
3.图4中转动自行车的脚踏板,小齿轮边缘上的点和后轮边缘上的点谁运动的快?理由是什么? 知道圆周运动不仅有运动快慢,还有转动快慢,具有初步的转动观念(物理观念)
4.描述运动的快慢和描述转动快慢,如何在名称上加以区分?
教学建议:
(1)思维引导建议:圆周运动是针对质点的运动来说的,在图1、图2、图3中的物体都应该选择其中的某一点进行研究。利用学生所熟悉的生活中的圆周运动引入课题,引导学生分析、概括这类运动的共同特点,得出圆周运动的定义。学生以前只接触运动快慢,没有涉及转动快慢,教学中要通过学生熟悉的自行车进行演示,结合问题,引发比较圆周运动快慢的不同方式的讨论。
(2)教学活动建议:对问题1、2,可让学生独立思考后回答,其他同学补充;对问题3,或让学生进行小组讨论后回答,也可让学生独立思考后回答,其他同学补充。
任务2:圆周运动的线速度和角速度
问题情景:如图5、6所示。
问题 问题指向的素养目标
1.如图5,电扇叶片上任意点的线速度方向如何确定?该方向与半径间的关系如何? 能根据曲线运动方向规律推断圆周运动线速度方向(科学思维)
知道圆周运动线速度方向与半径垂直(物理观念)
2.做圆周运动物体的运动路径长度如何确定?线速度大小如何确定? 能够根据描述运动快慢的要求确定线速度大小的定义方式(科学思维)
知道线速度大小的定义式(物理观念)
3.匀速圆周运动的线速度变化吗?匀速圆周运动是什么性质的运动? 知道匀速圆周运动是一种变速运动(物理观念)
4.如图6中,转动脚踏板,自行车大、小齿轮上的边缘点线速度大小相等吗?大、小齿轮转动的快慢也一样吗? 知道角速度的定义式和单位(物理观念)
能够类比线速度的定义方法,确定角速度的定义方式(科学思维)
5.前面已经给描述转动快慢的物理量取了一个名字叫角速度,角速度该怎样定义呢?根据定义式得到的角速度的单位是什么?
6.匀速圆周运动的角速度如何变化?电扇同一叶片上离转轴距离不同的各点,角速度是否相同? 知道匀速圆周运动角速度不变(物理观念)
能够根据角速度的定义式分析、解决问题(科学思维)
教学建议:
(1)思维引导建议:考虑到学生已经具有的曲线运动的速度方向知识,圆周运动属于曲线运动的一种,可以先让学生确定圆周运动线速度方向。考虑到学生的实际和历史上对圆周运动线速度大小的定义,线速度的大小定义为弧长与时间的比值,即线速度的定义式为。
(2)教学活动建议:对问题1,考虑到学生已经有分析、推理的依据,可让学生独立思考后回答;对于问题2,可以让学生独立思考后回答;对问题3、4、5、6,考虑到学生已经具有分析、推理的基础,可让学生独立思考后回答。
任务3:圆周运动的周期和转速及各物理量间的关系
问题情景:如图5所示。
问题 问题指向的素养目标
如图5,电扇叶片上的每一点都做匀速圆周运动,这种运动整体上具有什么特性?该用什么物理量来描述运动具有的周期性? 知道周期和转速的意义(物理观念)
2.周期的定义是什么?单位是什么?周期的物理意义是什么?
3.转速的定义是什么?单位是什么?转速的物理意义是什么?
4.选择电扇开关的不同挡位,电扇运动时的周期和转速有什么关系?你的猜想是什么?能证明吗? 知道周期和转速相互之间的关系(物理观念)
5.圆周中的弧长和对应圆心角之间有什么关系? 能用已有知识推导线速度、角速度、周期(转速)、半径间的关系(科学思维)知道线速度、角速度、周期(转速)、半径间的关系(物理观念)
6.本节课学到了哪些物理量?你能列出这些物理量并推导出相互之间的关系吗?
教学建议:
思维引导建议:通过学生熟悉的电扇,让学生体会到圆周运动具有周而复始的周期性特点,应该用体现这种特点的物理量来描述。具体来说,可以利用转一周所用的时间,即周期来比较运动的快慢,也可以用单位时间内转过的圈数也即是转速来比较运动的快慢,从而得出周期和转速的定义式。数学中的弧长与半径、圆心角的关系是推导的基础,通过问题可以帮助学生回忆。
(2)教学活动建议:对问题1,可在学生独立思考的基础上,让学生小组讨论后再回答;对问题2、3,可让学生独立回答,其他同学补充完善;对问题4,可先小组讨论再回答;对问题5,可让学生独立回答,其他同学补充;对问题6,让学生独立推导,完成后展示,其他同学补充完善。
任务4:“同带”关联和“同轴”关联的约束关系
问题情景:如图7、8所示。
问题 问题指向的素养目标
1.图7后轮上的A、B和D三点的角速度有什么关系?为什么? 知道同轴转动的物体角速度相同,皮带、摩擦约束的转轮边缘点线速度相等(物理观念)
能分析与归纳同轴转动和皮带轮、摩擦轮之间的约束关系(科学思维)
2.图7大齿轮上的E、F、G、H四点的角速度有什么关系?为什么?
3.角速度相等的这些点具有什么特点?你能得到什么结论?
4.图7链条上各点的线速度大小有什么关系?为什么?
5.图7大齿轮边缘点与小齿轮边缘点的线速度大小有什么关系?为什么?如果是皮带关联,或者齿轮直接关联,边缘点的线速度大小还相等吗?
6.线速度大小相等的这些点具有什么特点?你能得到什么结论?
7.有人说图8中用打点计时器测得的线带速度大小就是转盘边缘点线速度的大小,你认为正确吗?为什么? 知道皮带约束的转轮边缘点线速度相等(物理观念)
体会物理学解决实际问题的实用价值,激发学习物理学的兴趣(科学态度与责任)
教学建议:
(1)思维引导建议:根据图7,先引导学生根据定义得出后轮上的A、B、D三点的角速度相等和大齿轮上的E、F、G、H四点的角速度相等,然后引导学生分析、归纳得出同轴转动时角速度相等。根据图7,先引导学生根据定义得出链条上各点的线速度大小相等,考虑到齿轮与链条的同步运动,可以推得大齿轮和小齿轮边缘点的线速度大小相等,进一步推广到皮带关联与齿轮直接关联,然后引导学生分析、归纳线速度相等的条件是关联物之间的“等弧长”特点,这一特点能够很好地解释图8的实验原理。
(2)教学活动建议:对问题1、2,可让学生独立回答;对问题3,先让学生独立思考,然后小组讨论后再回答;对问题4,可让学生独立回答;对问题5、6,先让学生独立思考,然后小组讨论后再回答;对问题7,可让学生独立回答,其他同学补充。
一、任务分解
二、教学活动
任务1:圆周运动及快慢的描述
问题情景:如图1、2、3、4所示。
问题 问题指向的素养目标
1.图1、图2、图3中物体上的某一点,其运动有什么共同的特点? 知道圆周运动及匀速圆周运动的意义(物理观念)
2.图1和图2、图3中物体的圆周运动有什么不同之处?
3.图4中转动自行车的脚踏板,小齿轮边缘上的点和后轮边缘上的点谁运动的快?理由是什么? 知道圆周运动不仅有运动快慢,还有转动快慢,具有初步的转动观念(物理观念)
4.描述运动的快慢和描述转动快慢,如何在名称上加以区分?
教学建议:
(1)思维引导建议:圆周运动是针对质点的运动来说的,在图1、图2、图3中的物体都应该选择其中的某一点进行研究。利用学生所熟悉的生活中的圆周运动引入课题,引导学生分析、概括这类运动的共同特点,得出圆周运动的定义。学生以前只接触运动快慢,没有涉及转动快慢,教学中要通过学生熟悉的自行车进行演示,结合问题,引发比较圆周运动快慢的不同方式的讨论。
(2)教学活动建议:对问题1、2,可让学生独立思考后回答,其他同学补充;对问题3,或让学生进行小组讨论后回答,也可让学生独立思考后回答,其他同学补充。
任务2:圆周运动的线速度和角速度
问题情景:如图5、6所示。
问题 问题指向的素养目标
1.如图5,电扇叶片上任意点的线速度方向如何确定?该方向与半径间的关系如何? 能根据曲线运动方向规律推断圆周运动线速度方向(科学思维)
知道圆周运动线速度方向与半径垂直(物理观念)
2.做圆周运动物体的运动路径长度如何确定?线速度大小如何确定? 能够根据描述运动快慢的要求确定线速度大小的定义方式(科学思维)
知道线速度大小的定义式(物理观念)
3.匀速圆周运动的线速度变化吗?匀速圆周运动是什么性质的运动? 知道匀速圆周运动是一种变速运动(物理观念)
4.如图6中,转动脚踏板,自行车大、小齿轮上的边缘点线速度大小相等吗?大、小齿轮转动的快慢也一样吗? 知道角速度的定义式和单位(物理观念)
能够类比线速度的定义方法,确定角速度的定义方式(科学思维)
5.前面已经给描述转动快慢的物理量取了一个名字叫角速度,角速度该怎样定义呢?根据定义式得到的角速度的单位是什么?
6.匀速圆周运动的角速度如何变化?电扇同一叶片上离转轴距离不同的各点,角速度是否相同? 知道匀速圆周运动角速度不变(物理观念)
能够根据角速度的定义式分析、解决问题(科学思维)
教学建议:
(1)思维引导建议:考虑到学生已经具有的曲线运动的速度方向知识,圆周运动属于曲线运动的一种,可以先让学生确定圆周运动线速度方向。考虑到学生的实际和历史上对圆周运动线速度大小的定义,线速度的大小定义为弧长与时间的比值,即线速度的定义式为。
(2)教学活动建议:对问题1,考虑到学生已经有分析、推理的依据,可让学生独立思考后回答;对于问题2,可以让学生独立思考后回答;对问题3、4、5、6,考虑到学生已经具有分析、推理的基础,可让学生独立思考后回答。
任务3:圆周运动的周期和转速及各物理量间的关系
问题情景:如图5所示。
问题 问题指向的素养目标
如图5,电扇叶片上的每一点都做匀速圆周运动,这种运动整体上具有什么特性?该用什么物理量来描述运动具有的周期性? 知道周期和转速的意义(物理观念)
2.周期的定义是什么?单位是什么?周期的物理意义是什么?
3.转速的定义是什么?单位是什么?转速的物理意义是什么?
4.选择电扇开关的不同挡位,电扇运动时的周期和转速有什么关系?你的猜想是什么?能证明吗? 知道周期和转速相互之间的关系(物理观念)
5.圆周中的弧长和对应圆心角之间有什么关系? 能用已有知识推导线速度、角速度、周期(转速)、半径间的关系(科学思维)知道线速度、角速度、周期(转速)、半径间的关系(物理观念)
6.本节课学到了哪些物理量?你能列出这些物理量并推导出相互之间的关系吗?
教学建议:
思维引导建议:通过学生熟悉的电扇,让学生体会到圆周运动具有周而复始的周期性特点,应该用体现这种特点的物理量来描述。具体来说,可以利用转一周所用的时间,即周期来比较运动的快慢,也可以用单位时间内转过的圈数也即是转速来比较运动的快慢,从而得出周期和转速的定义式。数学中的弧长与半径、圆心角的关系是推导的基础,通过问题可以帮助学生回忆。
(2)教学活动建议:对问题1,可在学生独立思考的基础上,让学生小组讨论后再回答;对问题2、3,可让学生独立回答,其他同学补充完善;对问题4,可先小组讨论再回答;对问题5,可让学生独立回答,其他同学补充;对问题6,让学生独立推导,完成后展示,其他同学补充完善。
任务4:“同带”关联和“同轴”关联的约束关系
问题情景:如图7、8所示。
问题 问题指向的素养目标
1.图7后轮上的A、B和D三点的角速度有什么关系?为什么? 知道同轴转动的物体角速度相同,皮带、摩擦约束的转轮边缘点线速度相等(物理观念)
能分析与归纳同轴转动和皮带轮、摩擦轮之间的约束关系(科学思维)
2.图7大齿轮上的E、F、G、H四点的角速度有什么关系?为什么?
3.角速度相等的这些点具有什么特点?你能得到什么结论?
4.图7链条上各点的线速度大小有什么关系?为什么?
5.图7大齿轮边缘点与小齿轮边缘点的线速度大小有什么关系?为什么?如果是皮带关联,或者齿轮直接关联,边缘点的线速度大小还相等吗?
6.线速度大小相等的这些点具有什么特点?你能得到什么结论?
7.有人说图8中用打点计时器测得的线带速度大小就是转盘边缘点线速度的大小,你认为正确吗?为什么? 知道皮带约束的转轮边缘点线速度相等(物理观念)
体会物理学解决实际问题的实用价值,激发学习物理学的兴趣(科学态度与责任)
教学建议:
(1)思维引导建议:根据图7,先引导学生根据定义得出后轮上的A、B、D三点的角速度相等和大齿轮上的E、F、G、H四点的角速度相等,然后引导学生分析、归纳得出同轴转动时角速度相等。根据图7,先引导学生根据定义得出链条上各点的线速度大小相等,考虑到齿轮与链条的同步运动,可以推得大齿轮和小齿轮边缘点的线速度大小相等,进一步推广到皮带关联与齿轮直接关联,然后引导学生分析、归纳线速度相等的条件是关联物之间的“等弧长”特点,这一特点能够很好地解释图8的实验原理。
(2)教学活动建议:对问题1、2,可让学生独立回答;对问题3,先让学生独立思考,然后小组讨论后再回答;对问题4,可让学生独立回答;对问题5、6,先让学生独立思考,然后小组讨论后再回答;对问题7,可让学生独立回答,其他同学补充。
