苏科版七年级下册数学课件 8.5小结与思考(共13张ppt)
文档属性
| 名称 | 苏科版七年级下册数学课件 8.5小结与思考(共13张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 263.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览





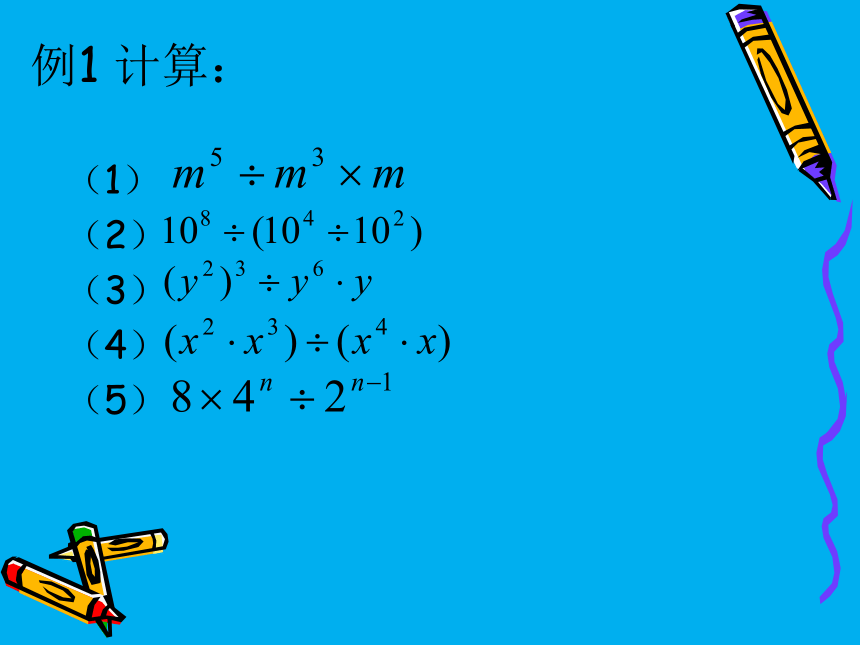
文档简介
幂的运算 小结与思考
学习本章需关注的几个问题
◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它
还可以表示一个单项式,甚至还可以表示一个多项式.换句话说,
将底数看作是一个“整体”即可.
◆注意上述各式的逆向应用.如计算,可先逆用同底数幂的乘法法
则将写成,再逆用积的乘方法则计算,由此不难得到结果为1.
◆通过对式子的变形,进一步领会转化的数学思想方法.如同底数幂的乘法就是将乘法运算转化为指数的加法运算,同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等.
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法.
例1 计算:
(1)
(2)
(3)
(4)
(5)
例2 计算:
(1)
(2)
(3)
例3
巩固练习;
1.若a·a3·am=a8,则m=_______;
2.若a5·(an)3=a11,则n=______.
3.如果(a4)3÷(a2)5=64,且a<0,那么a=_______.
4.某生物教师在显微镜下发现,某种植物的细胞直径约为0.000 12 mm,用科学记数法表示为_ ______ mm.
4
2
-8
1.2×10-4
5.若a2n=3,则2a6n-50=_______.
6.若3n=2,3m=5,则32m+3n-1的值为_______.
7.下列运算正确的是 ( )
A.a3·a4 =a12 B.a3+a3=2a6
C.a3÷a3=0 D.3a2·5a3=15a5
8.计算6m3÷(-3m2)的结果是 ( )
A.-3m B.-2m C.2m D.3m
4
26
D
B
9.如果a=(-2012)0 ,b=(-0.1)-1,
c=-1,那么a、b、c三个数的大小为( )
A.a>b>c B.c>a>b
C.a>c>b D.c>b>a
C
小结与思考:
通过本节课的学习你有哪些收获?
你还有什么疑惑?
谢 谢!
再 见!
学习本章需关注的几个问题
◆上述各式子中的底数字母不仅仅表示一个数、一个字母,它
还可以表示一个单项式,甚至还可以表示一个多项式.换句话说,
将底数看作是一个“整体”即可.
◆注意上述各式的逆向应用.如计算,可先逆用同底数幂的乘法法
则将写成,再逆用积的乘方法则计算,由此不难得到结果为1.
◆通过对式子的变形,进一步领会转化的数学思想方法.如同底数幂的乘法就是将乘法运算转化为指数的加法运算,同底数幂的除法就是将除法运算转化为指数的减法运算,幂的乘方就是将乘方运算转化为指数的乘法运算等.
◆在经历上述各个式子的推导过程中,进一步领悟“通过观察、猜想、验证与发现法则、规律”这一重要的数学研究的方法,学习并体会从特殊到一般的归纳推理的数学思想方法.
例1 计算:
(1)
(2)
(3)
(4)
(5)
例2 计算:
(1)
(2)
(3)
例3
巩固练习;
1.若a·a3·am=a8,则m=_______;
2.若a5·(an)3=a11,则n=______.
3.如果(a4)3÷(a2)5=64,且a<0,那么a=_______.
4.某生物教师在显微镜下发现,某种植物的细胞直径约为0.000 12 mm,用科学记数法表示为_ ______ mm.
4
2
-8
1.2×10-4
5.若a2n=3,则2a6n-50=_______.
6.若3n=2,3m=5,则32m+3n-1的值为_______.
7.下列运算正确的是 ( )
A.a3·a4 =a12 B.a3+a3=2a6
C.a3÷a3=0 D.3a2·5a3=15a5
8.计算6m3÷(-3m2)的结果是 ( )
A.-3m B.-2m C.2m D.3m
4
26
D
B
9.如果a=(-2012)0 ,b=(-0.1)-1,
c=-1,那么a、b、c三个数的大小为( )
A.a>b>c B.c>a>b
C.a>c>b D.c>b>a
C
小结与思考:
通过本节课的学习你有哪些收获?
你还有什么疑惑?
谢 谢!
再 见!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
