苏科版八年级下册数学 11.2反比例函数的图象与性质(2) 课件(共16张ppt)
文档属性
| 名称 | 苏科版八年级下册数学 11.2反比例函数的图象与性质(2) 课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览




文档简介
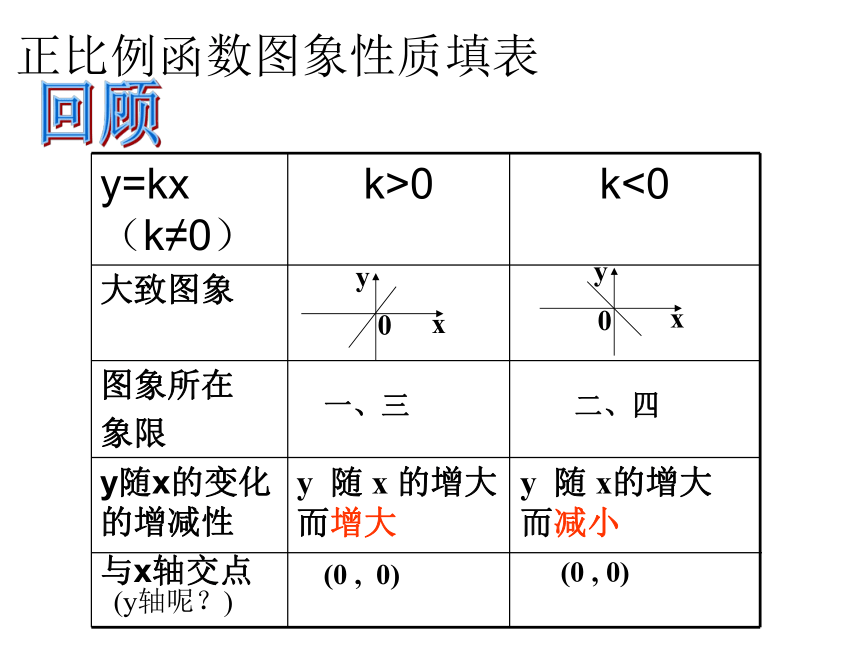
正比例函数图象性质填表
y=kx(k≠0)
k>0
k<0
大致图象
图象所在
象限
y随x的变化的增减性
与x轴交点
x
y
0
x
y
0
一、三
二、四
y 随 x 的增大而增大
y 随 x的增大而减小
(0 , 0)
(0 , 0)
(y轴呢?)
观察课本P.66、P.67练习中反比例函数的
图象思考下列问题:
(1)每个函数图象分别在哪些象限?
(2)在每个象限内,随着x的增大, y是
怎样变化的?
(3)反比例函数的图象与x轴有交点吗?
与y轴有交点吗?为什么?
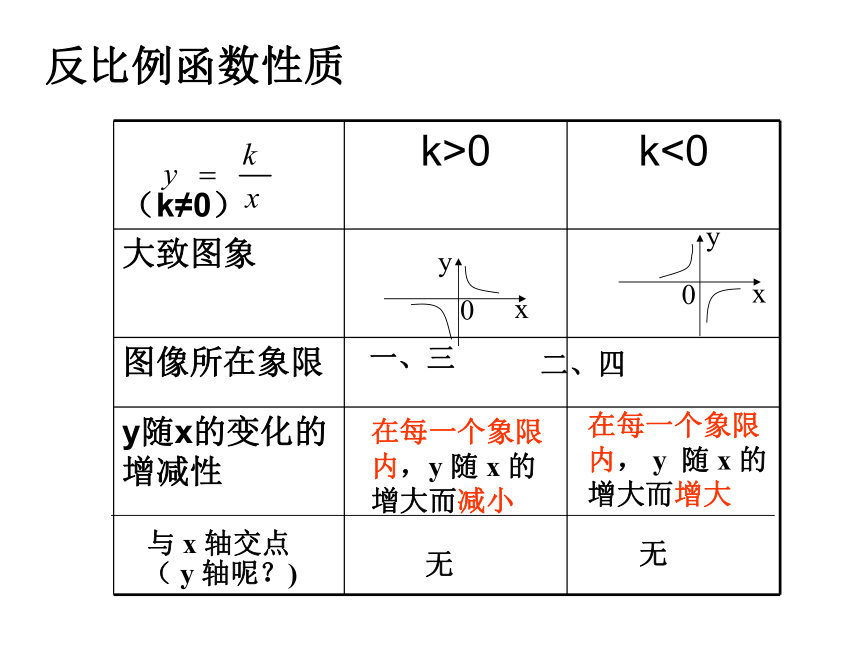
(k≠0)
k>0
k<0
大致图象
图像所在象限
y随x的变化的增减性
x
y
0
一、三
二、四
在每一个象限内,y 随 x 的增大而减小
在每一个象限内, y 随 x 的增大而增大
无
无
与 x 轴交点
( y 轴呢?)
反比例函数性质
x
y
0
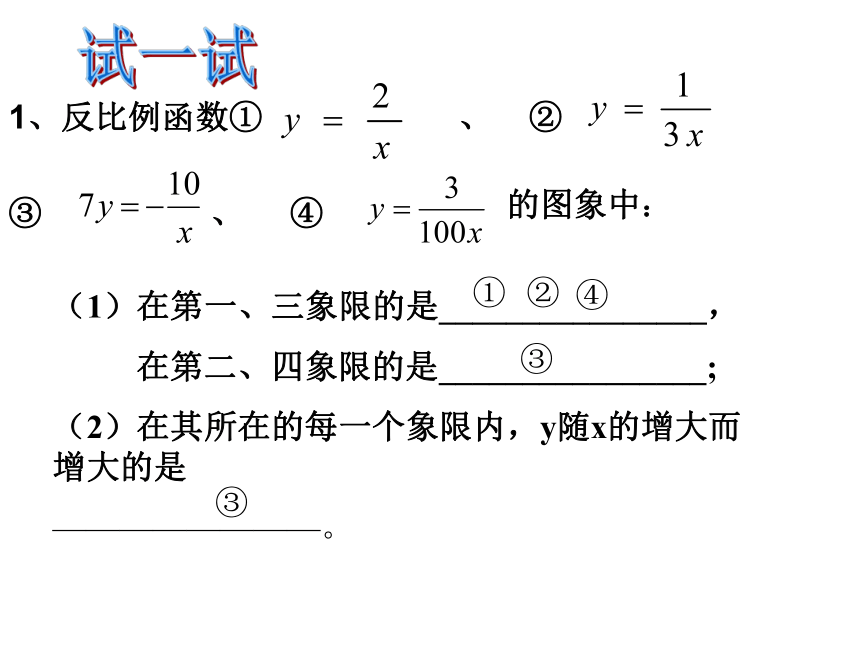
1、反比例函数① 、 ②
③ 、 ④
的图象中:
(1)在第一、三象限的是________________,
在第二、四象限的是________________;
(2)在其所在的每一个象限内,y随x的增大而增大的是
————————。
③
④
①
②
③
2、 已知反比例函数 的图象
在第一、三象限,那么m的取值范围是
________ .
已知反比例函数 的图像经过点A(2,-4).
(1)求k的值.
(2)这个函数的图像在哪几个象限?在每一个象限内,y随x的增大怎样变化?
(3)画出这个函数的图像.
(4)点B( ,-16) , C(-3, 5)在这个函数图像
上吗?
已知反比例函数的图象经过点A(-6,-3).
(1)写出函数关系式;
(2)这个函数的图象在那几个象限?在每个象限内,
y随x的增大怎样变化?
(3)点B(4, )、C(2,-5)在这个函数图象上吗?
1、若点(3,-4)在反比例函数 的图象上,那么下列各点中,在此图象上的是( )
A(3,4) B(-2,-6)
C(-2,6) D(-3,-4)
C
2、如图是反比例函数 的图象的一个
分支.根据图象填空:
(1) 比例系数k___0 ,其
图象上横坐标为正的点
在第______象限;
(2)如果点A(x1,y1)、B(x2,y2)在这个函数图象上,且x1>x2>0, 则y1-y2的值为( )
A、正数 B、负数
C、非负数 D、非正数
y
x
o
<
四
A
A
B
x1
y1
x2
y2
探索发现
思考并交流课本P69的“探索”
你得出结论是什么?
x
y
O
反比例函数 的图象是中心对称图形,它的对称中心是坐标原点.
正比例函数y=3x的图象与反比例函
数 的图象有一个交点
A的横坐标为3.
(1)求k的值.
(2)另一个交点B的坐标是什么?
(3)过A点作AC∥y轴,过B点作BC∥x轴,则△ABC的面积是_______.
o
A
B
C
x
y
54
已知k<0,则函数 y1=kx,
y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2 = 在同一坐标系中
的图象大致是 ( )
x
k
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
谈谈你的收获
反比例函数的性质及应用
函数
正比例函数
反比例函数
解析式
图象形状
K > 0
K < 0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y 随 x 的增大而增大
一三象限
二四象限
y 随 x 的增大而减小
在每个象限内, y 随 x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y 随 x 的增大而减小
y=kx(k≠0)
k>0
k<0
大致图象
图象所在
象限
y随x的变化的增减性
与x轴交点
x
y
0
x
y
0
一、三
二、四
y 随 x 的增大而增大
y 随 x的增大而减小
(0 , 0)
(0 , 0)
(y轴呢?)
观察课本P.66、P.67练习中反比例函数的
图象思考下列问题:
(1)每个函数图象分别在哪些象限?
(2)在每个象限内,随着x的增大, y是
怎样变化的?
(3)反比例函数的图象与x轴有交点吗?
与y轴有交点吗?为什么?
(k≠0)
k>0
k<0
大致图象
图像所在象限
y随x的变化的增减性
x
y
0
一、三
二、四
在每一个象限内,y 随 x 的增大而减小
在每一个象限内, y 随 x 的增大而增大
无
无
与 x 轴交点
( y 轴呢?)
反比例函数性质
x
y
0
1、反比例函数① 、 ②
③ 、 ④
的图象中:
(1)在第一、三象限的是________________,
在第二、四象限的是________________;
(2)在其所在的每一个象限内,y随x的增大而增大的是
————————。
③
④
①
②
③
2、 已知反比例函数 的图象
在第一、三象限,那么m的取值范围是
________ .
已知反比例函数 的图像经过点A(2,-4).
(1)求k的值.
(2)这个函数的图像在哪几个象限?在每一个象限内,y随x的增大怎样变化?
(3)画出这个函数的图像.
(4)点B( ,-16) , C(-3, 5)在这个函数图像
上吗?
已知反比例函数的图象经过点A(-6,-3).
(1)写出函数关系式;
(2)这个函数的图象在那几个象限?在每个象限内,
y随x的增大怎样变化?
(3)点B(4, )、C(2,-5)在这个函数图象上吗?
1、若点(3,-4)在反比例函数 的图象上,那么下列各点中,在此图象上的是( )
A(3,4) B(-2,-6)
C(-2,6) D(-3,-4)
C
2、如图是反比例函数 的图象的一个
分支.根据图象填空:
(1) 比例系数k___0 ,其
图象上横坐标为正的点
在第______象限;
(2)如果点A(x1,y1)、B(x2,y2)在这个函数图象上,且x1>x2>0, 则y1-y2的值为( )
A、正数 B、负数
C、非负数 D、非正数
y
x
o
<
四
A
A
B
x1
y1
x2
y2
探索发现
思考并交流课本P69的“探索”
你得出结论是什么?
x
y
O
反比例函数 的图象是中心对称图形,它的对称中心是坐标原点.
正比例函数y=3x的图象与反比例函
数 的图象有一个交点
A的横坐标为3.
(1)求k的值.
(2)另一个交点B的坐标是什么?
(3)过A点作AC∥y轴,过B点作BC∥x轴,则△ABC的面积是_______.
o
A
B
C
x
y
54
已知k<0,则函数 y1=kx,
y2= 在同一坐标系中的图象大致是 ( )
x
k
2. 已知k>0,则函数 y1=kx+k与y2 = 在同一坐标系中
的图象大致是 ( )
x
k
x
y
0
x
y
0
x
y
0
x
y
0
(A)
(B)
(C)
(D)
(A)
x
y
0
x
y
0
(B)
(C)
(D)
x
y
0
x
y
0
D
C
谈谈你的收获
反比例函数的性质及应用
函数
正比例函数
反比例函数
解析式
图象形状
K > 0
K < 0
位置
增减性
位置
增减性
y=kx ( k≠0 的常数)
( k≠0的常数 )
y =
x
k
直线
双曲线
一三象限
y 随 x 的增大而增大
一三象限
二四象限
y 随 x 的增大而减小
在每个象限内, y 随 x的增大而增大
比较正比例函数和反比例函数的区别
二四象限
在每个象限内,y 随 x 的增大而减小
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
