江西省兴国县平川中学2012届高三年级第一次月考数学试卷理科
文档属性
| 名称 | 江西省兴国县平川中学2012届高三年级第一次月考数学试卷理科 |

|
|
| 格式 | zip | ||
| 文件大小 | 221.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-21 00:00:00 | ||
图片预览




文档简介
平川中学高三年级第一次月考数学试卷(理)
2011/8/30
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知z1=1-3i,z2=2a+i,且z2=,则实数a的值为
A. B. C.- D.-
2、数列{an}满足a1=2,an=1-(n=2, 3, 4, …),则a2011=
A.-1 B.2 C. D.-2
3、在△ABC中,角A、B、C的对边分别为a、b、c,若(a2+c2-b2)tanB=ac,则角B的值为
A. B. C.或 D.或
4、函数f(x)满足f(x+1)和f(x)都是偶函数,且当0≤x≤1时,f(x)=log3(x+1),则函数g(x)=f(x)-在[-4, 4]上的零点个数为
A.2 B.4
C.6 D.8
5、如右图是计算13+23+…+103的程序框图,图中的①,②分别是
A.①s=s+i,②i=i+1
B.①s=s+i3,②i=i+1
C.①i=i+1,②s=s+i
D.①i=i+1,②s=s+i3
6、一个正三棱柱的三视图如右图所示,则正三棱柱的外接球的表面积是
A.
B.
C.
D.
7、设F1,F2分别是双曲线的左、右焦点,若双曲线上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,则双曲线的离心率为
A. B. C. D.
8、已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得=4a1,则的最小值为
A. B. C. D.不存在
9、如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形内部的概率是
A. B.
C. D.
10、函数f(x)的定义域为D,若对任意x1,x2∈D,当x1A. B. C.1 D.
二.填空题:本大题共5小题,每小题5分,共25分.把答案填写在题中横线上.
(一)必做题(11~14题)
11、根据工作需要,现从4名女教师,a名男教师中选3名教师组成援川团队,其中a=,要求团队中男、女教师都有,则不同的组队方案种数为 。
12、记f(n)=,通过计算f(1),f(2),f(3)的值,归纳出f(n)= 。
13、已知关于x的方程x2+(1+a)x+1+a+b=0(a, b∈R)的两根分别为x1,x2,且014、下列给出的四个命题中:
①已知数列{an},那么对任意n∈N*,“点Pn(n, an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)与坐标轴有4个交点,分别为A(x1, 0),B(x2, 0),C(0, y1),D(0, y2),则x1x2-y1y2=0;
④将函数y=cos2x的图象向右平移个单位,设函数y=sin(2x-)的图象,其中真命题的序号为 。
(二)选做题(注意:考生只能从①②中选做一题)
15、①已知函数f(x)=|x-k|+|x-2k|,若对任意x∈R,f(x)≥f(3)=f(4)都成立,则实数k的取值范围为 。
②已知直线l:(t为参数)与曲线C:ρ=4交于A、B两点,则线段AB的长为 。
三.解答题:本大题共6小题,共75分。其中(16)~(19)每小题12分,(20)题13分,(21)题14分.解答应写出文字说明,证明过程和演算步骤
16、(本小题满分12分)
已知函数f(x)=sin2x-cos2x-,x∈R。
(1)求函数f(x)的最小正周期和最小值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c=,f(C)=0,若向量=(1, sinA)与向量=(2, sinB)共线,求a,b的值。
17、(本小题满分12分)
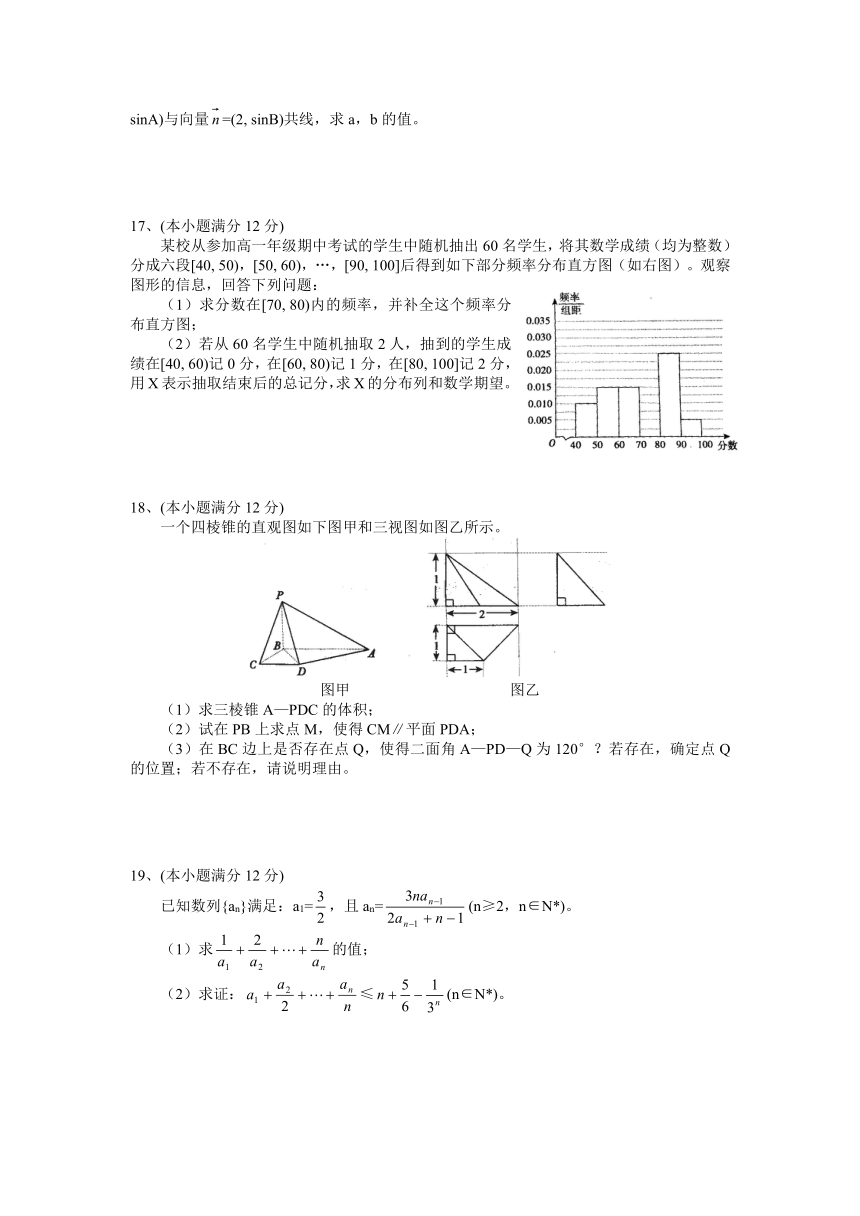
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40, 50),[50, 60),…,[90, 100]后得到如下部分频率分布直方图(如右图)。观察图形的信息,回答下列问题:
(1)求分数在[70, 80)内的频率,并补全这个频率分布直方图;
(2)若从60名学生中随机抽取2人,抽到的学生成绩在[40, 60)记0分,在[60, 80)记1分,在[80, 100]记2分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
18、(本小题满分12分)
一个四棱锥的直观图如下图甲和三视图如图乙所示。
图甲 图乙
(1)求三棱锥A—PDC的体积;
(2)试在PB上求点M,使得CM∥平面PDA;
(3)在BC边上是否存在点Q,使得二面角A—PD—Q为120°?若存在,确定点Q的位置;若不存在,请说明理由。
19、(本小题满分12分)
已知数列{an}满足:a1=,且an=(n≥2,n∈N*)。
(1)求的值;
(2)求证:≤(n∈N*)。
20、(本小题满分13分)
如右图,已知点P(4, 4),圆C:(x-m)2+y2=5(m<3)与椭圆E:(a>b>0)的一个公共点为A(3, 1),F1,F2分别是椭圆的左、右焦点,直线PF1与圆C相切。
(1)求m的值与椭圆E的方程;
(2)设D为直线PF1与圆C的切点,在椭圆E上是否存在点Q,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。
21、(本小题满分14分)
设函数f(x)=x2-mlnx,h(x)=x2-x+a。
(1)当a=0时,f(x)≥h(x)在(1, +∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1, 3]上恰有两个不同零点,求实数a的取值范围;
(3)是否存在实数m使函数f(x)和函数h(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由。
平川高三年级第一次月考数学试卷(理)
参考答案
2011/8/30
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
A B D D B C B A B A
二、填空题(每小题5分,共25分)
11、 70 12、
13、 14、 ①③④
15、① [2, 3] ②
三.解答题:本大题共6小题,共75分。其中(16)~(19)每小题12分,(20)题13分,(21)题14分.解答应写出文字说明,证明过程和演算步骤
16、(本小题满分12分)
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分13分)
21、(本小题满分14分)
y=x2
2011/8/30
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知z1=1-3i,z2=2a+i,且z2=,则实数a的值为
A. B. C.- D.-
2、数列{an}满足a1=2,an=1-(n=2, 3, 4, …),则a2011=
A.-1 B.2 C. D.-2
3、在△ABC中,角A、B、C的对边分别为a、b、c,若(a2+c2-b2)tanB=ac,则角B的值为
A. B. C.或 D.或
4、函数f(x)满足f(x+1)和f(x)都是偶函数,且当0≤x≤1时,f(x)=log3(x+1),则函数g(x)=f(x)-在[-4, 4]上的零点个数为
A.2 B.4
C.6 D.8
5、如右图是计算13+23+…+103的程序框图,图中的①,②分别是
A.①s=s+i,②i=i+1
B.①s=s+i3,②i=i+1
C.①i=i+1,②s=s+i
D.①i=i+1,②s=s+i3
6、一个正三棱柱的三视图如右图所示,则正三棱柱的外接球的表面积是
A.
B.
C.
D.
7、设F1,F2分别是双曲线的左、右焦点,若双曲线上存在点A,使∠F1AF2=90°,且|AF1|=3|AF2|,则双曲线的离心率为
A. B. C. D.
8、已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得=4a1,则的最小值为
A. B. C. D.不存在
9、如图所示,若向圆x2+y2=2内随机投一点(该点落在圆x2+y2=2内任何一点是等可能的),则所投的点落在圆与y轴及曲线y=x2(x≥0)围成的阴影图形内部的概率是
A. B.
C. D.
10、函数f(x)的定义域为D,若对任意x1,x2∈D,当x1
二.填空题:本大题共5小题,每小题5分,共25分.把答案填写在题中横线上.
(一)必做题(11~14题)
11、根据工作需要,现从4名女教师,a名男教师中选3名教师组成援川团队,其中a=,要求团队中男、女教师都有,则不同的组队方案种数为 。
12、记f(n)=,通过计算f(1),f(2),f(3)的值,归纳出f(n)= 。
13、已知关于x的方程x2+(1+a)x+1+a+b=0(a, b∈R)的两根分别为x1,x2,且0
①已知数列{an},那么对任意n∈N*,“点Pn(n, an)都在直线y=2x+1上”是“{an}为等差数列”的充分不必要条件;
②“m=-2”是“直线(m+2)x+my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)与坐标轴有4个交点,分别为A(x1, 0),B(x2, 0),C(0, y1),D(0, y2),则x1x2-y1y2=0;
④将函数y=cos2x的图象向右平移个单位,设函数y=sin(2x-)的图象,其中真命题的序号为 。
(二)选做题(注意:考生只能从①②中选做一题)
15、①已知函数f(x)=|x-k|+|x-2k|,若对任意x∈R,f(x)≥f(3)=f(4)都成立,则实数k的取值范围为 。
②已知直线l:(t为参数)与曲线C:ρ=4交于A、B两点,则线段AB的长为 。
三.解答题:本大题共6小题,共75分。其中(16)~(19)每小题12分,(20)题13分,(21)题14分.解答应写出文字说明,证明过程和演算步骤
16、(本小题满分12分)
已知函数f(x)=sin2x-cos2x-,x∈R。
(1)求函数f(x)的最小正周期和最小值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c=,f(C)=0,若向量=(1, sinA)与向量=(2, sinB)共线,求a,b的值。
17、(本小题满分12分)
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其数学成绩(均为整数)分成六段[40, 50),[50, 60),…,[90, 100]后得到如下部分频率分布直方图(如右图)。观察图形的信息,回答下列问题:
(1)求分数在[70, 80)内的频率,并补全这个频率分布直方图;
(2)若从60名学生中随机抽取2人,抽到的学生成绩在[40, 60)记0分,在[60, 80)记1分,在[80, 100]记2分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
18、(本小题满分12分)
一个四棱锥的直观图如下图甲和三视图如图乙所示。
图甲 图乙
(1)求三棱锥A—PDC的体积;
(2)试在PB上求点M,使得CM∥平面PDA;
(3)在BC边上是否存在点Q,使得二面角A—PD—Q为120°?若存在,确定点Q的位置;若不存在,请说明理由。
19、(本小题满分12分)
已知数列{an}满足:a1=,且an=(n≥2,n∈N*)。
(1)求的值;
(2)求证:≤(n∈N*)。
20、(本小题满分13分)
如右图,已知点P(4, 4),圆C:(x-m)2+y2=5(m<3)与椭圆E:(a>b>0)的一个公共点为A(3, 1),F1,F2分别是椭圆的左、右焦点,直线PF1与圆C相切。
(1)求m的值与椭圆E的方程;
(2)设D为直线PF1与圆C的切点,在椭圆E上是否存在点Q,使△PDQ是以PD为底的等腰三角形?若存在,请指出共有几个这样的点?并说明理由。
21、(本小题满分14分)
设函数f(x)=x2-mlnx,h(x)=x2-x+a。
(1)当a=0时,f(x)≥h(x)在(1, +∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1, 3]上恰有两个不同零点,求实数a的取值范围;
(3)是否存在实数m使函数f(x)和函数h(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由。
平川高三年级第一次月考数学试卷(理)
参考答案
2011/8/30
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中只有一项是符合题目要求的)
1 2 3 4 5 6 7 8 9 10
A B D D B C B A B A
二、填空题(每小题5分,共25分)
11、 70 12、
13、 14、 ①③④
15、① [2, 3] ②
三.解答题:本大题共6小题,共75分。其中(16)~(19)每小题12分,(20)题13分,(21)题14分.解答应写出文字说明,证明过程和演算步骤
16、(本小题满分12分)
17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分12分)
20、(本小题满分13分)
21、(本小题满分14分)
y=x2
同课章节目录
