二次函数单元测试
图片预览



文档简介
2011---2012学年度九年级数学
第一次阶段性检测
一、选择题(10×4分=40分)
1、设抛物线y=x2+4x-k的顶点在x轴上,则k的值为( )
A -4 B 4 C -2 D 2
2、若点(2,5)、(4,5)是抛物线上的两个点,则它的对称轴是 ( )
A、x= B、 C、 D、
3、已知二次函数,当自变量取两个不同的值时,函数值相等,则当自变量取时的函数值与( )
A.时的函数值相等 B.时的函数值相等
C.时的函数值相等 D.时的函数值相等
4、一位篮球运动员站在罚球线后投篮,球入篮得分.下列图象中,可以大致反映篮球出手后到入篮框这一时间段内,篮球的高度与时间之间变化关系的是( )
5、若抛物线的顶点在轴的下方,则的取值范围是( )
A. B. C. D.
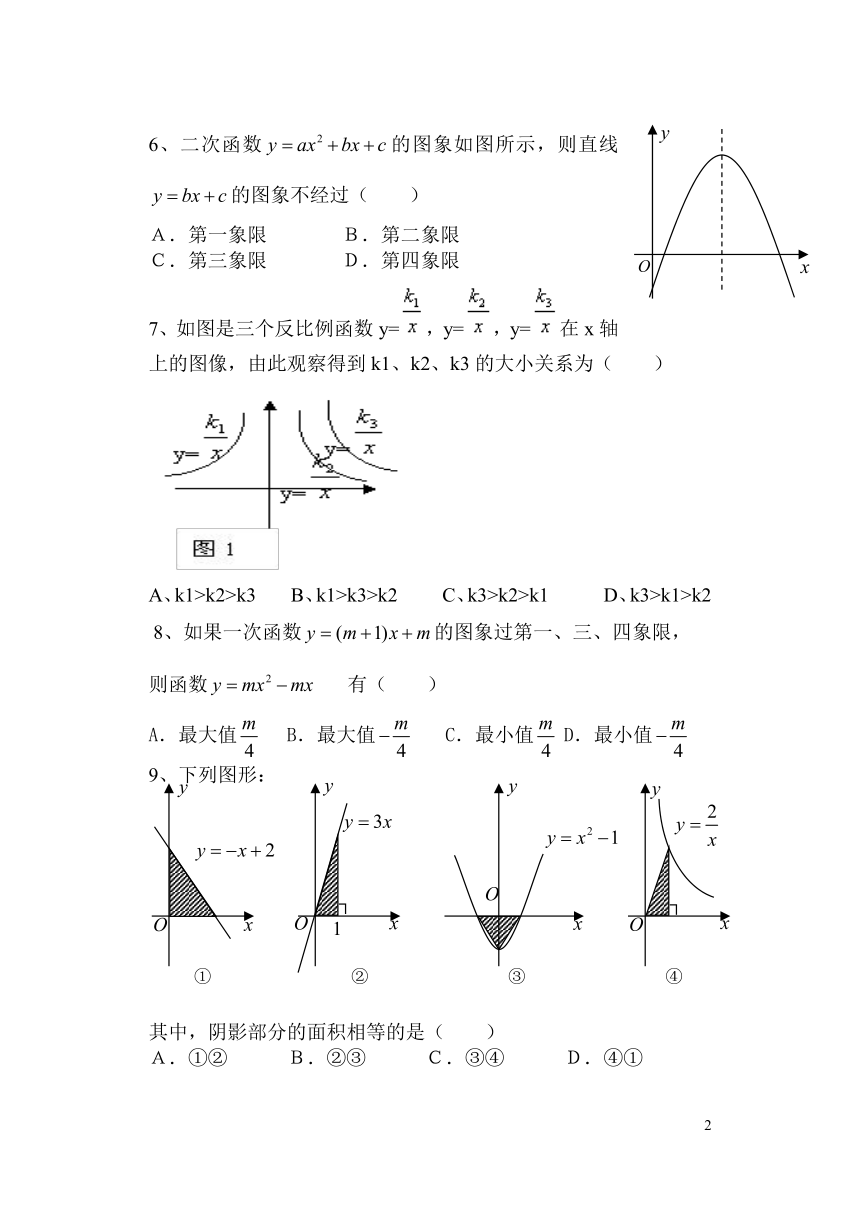
6、二次函数的图象如图所示,则直线的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7、如图是三个反比例函数y=,y=,y=在x轴上的图像,由此观察得到k1、k2、k3的大小关系为( )
A、k1>k2>k3 B、k1>k3>k2 C、k3>k2>k1 D、k3>k1>k2
8、如果一次函数的图象过第一、三、四象限,
则函数 有( )
A.最大值 B.最大值 C.最小值 D.最小值
9、下列图形:
其中,阴影部分的面积相等的是( )
A.①② B.②③ C.③④ D.④①
10、已知二次函数(a≠0)的图象开口向上,并经过点(-1,2),(1,0) . 下列结论正确的是( )
A. 当x>0时,函数值y随x的增大而增大
B. 当x>0时,函数值y随x的增大而减小
C. 存在一负数x。,使得当x当x> x。时,函数值y随x的增大而增大
D. 存在一正数x。,使得当x当x>x。时,函数值y随x的增大而增大
填空题(5×5分=25分)
已知y与(2x+1)成反比例且当x=0时,y=2,
那么当x=-1时,y=________。
12、函数的对称轴和轴相交于点,
则的值为____________.
13、二次函数图象上部分点的对应值如下表:
0 1 2 3 4
6 0 0 6
则使的的取值范围为 .
14、如图,在平面直角坐标系中,二次函数的图象过正方形的三个顶点,则的值是 .
15、反比例函数,当x>0时,y随x的增大而增大,则m的值是 。
简答题:
16、(8分)已知二次函数它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
(1)求此二次函数的解析式;
(2)写出函数值y为正数时,自变量x的取值范围。
(8分)正比例函数与反比例函数的图象都过A(,1)点.求:(1)正比例函数的解析式;
(2)正比例函数与反比例函数的另一个交点的坐标.
18、(10分)某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示)。若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米。
求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要
多少米,才能使喷出的水流不至于落在池外。
19、(10分)已知二次函数图象的顶点是,且过点.
(1)求二次函数的表达式,并在图中画出它的图象;
(2)求证:对任意实数,点都不在这个二次函数的图象上.
20、(11分)已知抛物线经过三点,当时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线顶点坐标;
(2)描出抛物线当时图象;
利用抛物线,写出为何值
时,.
21、(12分)某中学新校舍将于2011年元月动工。在新校舍内将按如图所示设计一个矩形花坛,花坛的长、宽分别为200 m、120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,
那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
22、(12分)已知两个关于的二次函数与
;当时,;且二次函数的图象的对称轴是直线.
(1)求的值;
(2)求函数的表达式;
(3)在同一直角坐标系内,问函数的图象与的图象是否有交点?请说明理由.
23、(14)容积率t是指在房地产开发中建筑面积与用地面积之比,即t=,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
班级 姓名 座位号
答 题 不 超 过 此 线
A.
B.
D.
C.
O
①
②
③
④
1
第一次阶段性检测
一、选择题(10×4分=40分)
1、设抛物线y=x2+4x-k的顶点在x轴上,则k的值为( )
A -4 B 4 C -2 D 2
2、若点(2,5)、(4,5)是抛物线上的两个点,则它的对称轴是 ( )
A、x= B、 C、 D、
3、已知二次函数,当自变量取两个不同的值时,函数值相等,则当自变量取时的函数值与( )
A.时的函数值相等 B.时的函数值相等
C.时的函数值相等 D.时的函数值相等
4、一位篮球运动员站在罚球线后投篮,球入篮得分.下列图象中,可以大致反映篮球出手后到入篮框这一时间段内,篮球的高度与时间之间变化关系的是( )
5、若抛物线的顶点在轴的下方,则的取值范围是( )
A. B. C. D.
6、二次函数的图象如图所示,则直线的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7、如图是三个反比例函数y=,y=,y=在x轴上的图像,由此观察得到k1、k2、k3的大小关系为( )
A、k1>k2>k3 B、k1>k3>k2 C、k3>k2>k1 D、k3>k1>k2
8、如果一次函数的图象过第一、三、四象限,
则函数 有( )
A.最大值 B.最大值 C.最小值 D.最小值
9、下列图形:
其中,阴影部分的面积相等的是( )
A.①② B.②③ C.③④ D.④①
10、已知二次函数(a≠0)的图象开口向上,并经过点(-1,2),(1,0) . 下列结论正确的是( )
A. 当x>0时,函数值y随x的增大而增大
B. 当x>0时,函数值y随x的增大而减小
C. 存在一负数x。,使得当x
D. 存在一正数x。,使得当x
填空题(5×5分=25分)
已知y与(2x+1)成反比例且当x=0时,y=2,
那么当x=-1时,y=________。
12、函数的对称轴和轴相交于点,
则的值为____________.
13、二次函数图象上部分点的对应值如下表:
0 1 2 3 4
6 0 0 6
则使的的取值范围为 .
14、如图,在平面直角坐标系中,二次函数的图象过正方形的三个顶点,则的值是 .
15、反比例函数,当x>0时,y随x的增大而增大,则m的值是 。
简答题:
16、(8分)已知二次函数它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3)。
(1)求此二次函数的解析式;
(2)写出函数值y为正数时,自变量x的取值范围。
(8分)正比例函数与反比例函数的图象都过A(,1)点.求:(1)正比例函数的解析式;
(2)正比例函数与反比例函数的另一个交点的坐标.
18、(10分)某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示)。若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米。
求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要
多少米,才能使喷出的水流不至于落在池外。
19、(10分)已知二次函数图象的顶点是,且过点.
(1)求二次函数的表达式,并在图中画出它的图象;
(2)求证:对任意实数,点都不在这个二次函数的图象上.
20、(11分)已知抛物线经过三点,当时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线顶点坐标;
(2)描出抛物线当时图象;
利用抛物线,写出为何值
时,.
21、(12分)某中学新校舍将于2011年元月动工。在新校舍内将按如图所示设计一个矩形花坛,花坛的长、宽分别为200 m、120 m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3x m、2x m.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168 x元,
那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852 = 7225,862 = 7396,872 = 7569)
22、(12分)已知两个关于的二次函数与
;当时,;且二次函数的图象的对称轴是直线.
(1)求的值;
(2)求函数的表达式;
(3)在同一直角坐标系内,问函数的图象与的图象是否有交点?请说明理由.
23、(14)容积率t是指在房地产开发中建筑面积与用地面积之比,即t=,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
(Ⅰ)试求图(1)中线段l的函数关系式,并求出开发该小区的用地面积;
(Ⅱ)求出图(2)中抛物线段c的函数关系式.
班级 姓名 座位号
答 题 不 超 过 此 线
A.
B.
D.
C.
O
①
②
③
④
1
