2020-2021学年八年级数学北师大版下册第六章 6.2 平行四边形的判定 同步练习题(word版含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册第六章 6.2 平行四边形的判定 同步练习题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 352.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览



文档简介
6.2平行四边形的判定
第二课时
【知识回顾】
定理:对角线___________的四边形是平行四边形.
如果两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离___________,这个距离称为___________________________.
【例题】
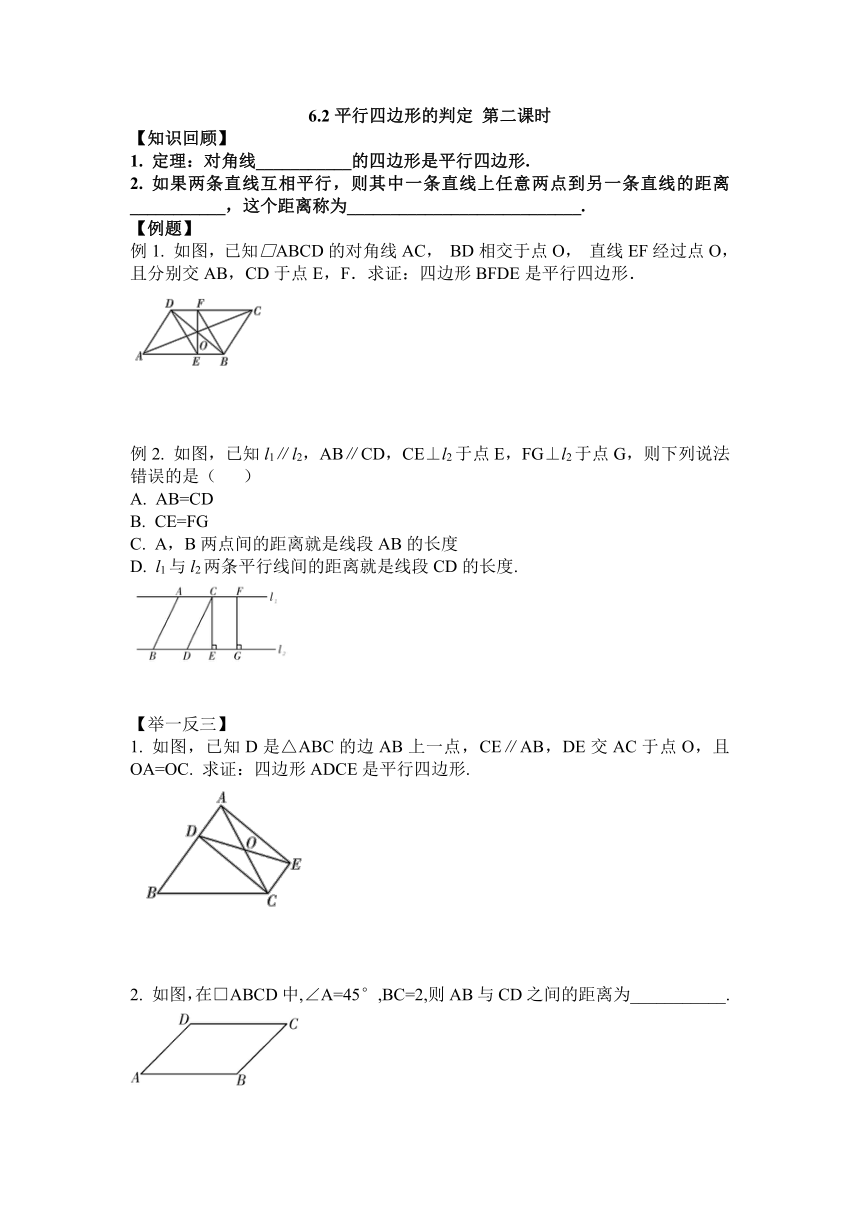
如图,已知□ABCD的对角线AC,
BD相交于点O,
直线EF经过点O,且分别交AB,CD于点E,F.求证:四边形BFDE是平行四边形.
如图,已知l1∥l2,AB∥CD,CE⊥l2于点E,FG⊥l2于点G,则下列说法错误的是(
)
AB=CD
CE=FG
A,B两点间的距离就是线段AB的长度
l1与l2两条平行线间的距离就是线段CD的长度.
【举一反三】
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.
求证:四边形ADCE是平行四边形.
如图,在□ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为___________.
【知识操练】
如图,在四边形ABCD中,已知AD∥BC,AC与BD相交于点O,则添加下列一个条件后,不能判定该四边形为平行四边形的是(
)
A.AD=BC
B.OA=OC
C.OD=OB
D.AB=DC
如图,已知直线a∥b,点A在直线a上,点B,C在直线b上,AC⊥直线b.
如果AB=5
cm,AC=4
cm,那么平行线a与b之间的距离为
(
)
A.
5
cm
B.
4
cm
C.
3
cm
D.
不能确定
如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,且AB=EF=2.
若△CEF的面积为5,则△ABD的面积为
(
)
A.
2
B.
4
C.
5
D.
10
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1,l2,l3上,且∠1=15°,则∠2=(
)
A.
15°
B.
35°
C.
30°
D.
25°
如图,在□ABCD中,AC,BD相交于点O,点E,F在对角线BD上.
下列条件不一定能判定四边形AECF是平行四边形的是(
)
A.
∠BAE=∠DCF
B.
∠AFD=∠CEB
C.
AE=CF
D.
OE=OF
在四边形ABCD中,对角线AC,BD相交于点O.
给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有(
)
3种
B.
4种
C.
5种
D.
6种
如图,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点.
给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF,其中不能判定四边形DEBF是平行四边形的有(
)
A.
0个
B.
1个
C.
2个
D.
3个
如图,在△ABC中,D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,则下列说法错误的是(
)
A.
△ABD≌△ECD
B.
连接BE,四边形ABEC为平行四边形
C.
DA=DE
D.
CE=CA
如图,AO=OC,BD=16
cm,则当OB=___________cm时,四边形ABCD是平行四边形.
如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,B,C,且相互平行.
若l1与l2的距离为3,l2与l3的距离为4,则正方形的面积是___________.
如图,在□ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
求证:四边形BFDE为平行四边形.
如图,在四边形ABCD中,∠A=∠ABC=90°,E是CD的中点,连接BE并延长与AD的延长线相交于点F.
求证:四边形BDFC是平行四边形.
如图,点E,F在四边形ABCD的对角线BD上,且DC∥AB,DC=AB,DE=FB.求证:∠ECF=∠FAE.
如图,平行四边形ABCD的两条对角线AC,BD相交于点O,E,G分别是OA,OC的中点,过点O作任一条直线交AD于点H,交BC于点F.
求证:
(1)OH=OF;
(2)HG=FE.
如图,在□ABCD中,对角线AC,BD相交于点O,过点O作两条直线,分别交AD,BC,AB,CD于点E,F,G,H.求证:四边形EGFH是平行四边形.
答案解析:
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,∠DCO=∠BAO.又∵∠AOE=∠COF,∴△AOE≌△COF(ASA).
∴OE=OF.又∵OB=OD,
∴四边形BFDE是平行四边形.
D
证明:∵AB∥CE,∴∠ADE=∠CED.
在△AOD和△COE中,
∠ADO=∠CEO,
∠AOD=∠COE,
OA=OC,
∴△AOD≌△COE(AAS).
∴OD=OE.
又∵OA=OC,
∴四边形ADCE是平行四边形.
1-8
DBCCCBBD
9.8
10.25
11.证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
又∵E,F分别是OA,OC的中点,
∴EO=AO,FO=CO.
∴EO=FO.
又∵BO=DO,∴四边形BFDE为平行四边形.
12.证明:∵∠A=∠ABC=90°,
∴BC∥AF.
∴∠CBE=∠DFE.
∵E是CD的中点,
∴CE=DE.
在△BEC和△FED中,
∴△BEC≌△FED(AAS).
∴BE=FE.
又∵CE=DE,
∴四边形BDFC是平行四边形.
证明:如答图,连接AC交BD于点O.
∵DC∥AB,DC=AB,
∴四边形ABCD是平行四边形.
∴OA=OC,OB=OD.
又∵DE=FB,
∴OE=OF.
∴四边形AFCE是平行四边形.
∴∠ECF=∠FAE.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,OD=OB.
∴∠ADO=∠CBO,∠DHO=∠BFO.
又∵OD=OB,∴△DHO≌△BFO(AAS).
∴OH=OF.
(2)连接HE,GF,如答图.
答图∵E,G分别是OA,OC的中点,且OA=OC,
∴OG=OE.
又由(1)知,OH=OF,
∴四边形HGFE是平行四边形.
∴HG=FE.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD∥BC.∴∠AEO=∠CFO.
∴△AEO≌△CFO(AAS).∴EO=FO.
同理可得△BGO≌△DHO(ASA).∴GO=HO.
∴四边形EGFH是平行四边形.
第二课时
【知识回顾】
定理:对角线___________的四边形是平行四边形.
如果两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离___________,这个距离称为___________________________.
【例题】
如图,已知□ABCD的对角线AC,
BD相交于点O,
直线EF经过点O,且分别交AB,CD于点E,F.求证:四边形BFDE是平行四边形.
如图,已知l1∥l2,AB∥CD,CE⊥l2于点E,FG⊥l2于点G,则下列说法错误的是(
)
AB=CD
CE=FG
A,B两点间的距离就是线段AB的长度
l1与l2两条平行线间的距离就是线段CD的长度.
【举一反三】
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.
求证:四边形ADCE是平行四边形.
如图,在□ABCD中,∠A=45°,BC=2,则AB与CD之间的距离为___________.
【知识操练】
如图,在四边形ABCD中,已知AD∥BC,AC与BD相交于点O,则添加下列一个条件后,不能判定该四边形为平行四边形的是(
)
A.AD=BC
B.OA=OC
C.OD=OB
D.AB=DC
如图,已知直线a∥b,点A在直线a上,点B,C在直线b上,AC⊥直线b.
如果AB=5
cm,AC=4
cm,那么平行线a与b之间的距离为
(
)
A.
5
cm
B.
4
cm
C.
3
cm
D.
不能确定
如图,已知直线a∥b,点A,B,C在直线a上,点D,E,F在直线b上,且AB=EF=2.
若△CEF的面积为5,则△ABD的面积为
(
)
A.
2
B.
4
C.
5
D.
10
如图,在△ABC中,∠ABC=90°,AB=BC,三角形的顶点分别在相互平行的三条直线l1,l2,l3上,且∠1=15°,则∠2=(
)
A.
15°
B.
35°
C.
30°
D.
25°
如图,在□ABCD中,AC,BD相交于点O,点E,F在对角线BD上.
下列条件不一定能判定四边形AECF是平行四边形的是(
)
A.
∠BAE=∠DCF
B.
∠AFD=∠CEB
C.
AE=CF
D.
OE=OF
在四边形ABCD中,对角线AC,BD相交于点O.
给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD,从中任选两个条件,能使四边形ABCD为平行四边形的选法有(
)
3种
B.
4种
C.
5种
D.
6种
如图,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点.
给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF,其中不能判定四边形DEBF是平行四边形的有(
)
A.
0个
B.
1个
C.
2个
D.
3个
如图,在△ABC中,D为BC的中点,连接AD,过点C作CE∥AB交AD的延长线于点E,则下列说法错误的是(
)
A.
△ABD≌△ECD
B.
连接BE,四边形ABEC为平行四边形
C.
DA=DE
D.
CE=CA
如图,AO=OC,BD=16
cm,则当OB=___________cm时,四边形ABCD是平行四边形.
如图,直线l1,l2,l3分别过正方形ABCD的三个顶点A,B,C,且相互平行.
若l1与l2的距离为3,l2与l3的距离为4,则正方形的面积是___________.
如图,在□ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
求证:四边形BFDE为平行四边形.
如图,在四边形ABCD中,∠A=∠ABC=90°,E是CD的中点,连接BE并延长与AD的延长线相交于点F.
求证:四边形BDFC是平行四边形.
如图,点E,F在四边形ABCD的对角线BD上,且DC∥AB,DC=AB,DE=FB.求证:∠ECF=∠FAE.
如图,平行四边形ABCD的两条对角线AC,BD相交于点O,E,G分别是OA,OC的中点,过点O作任一条直线交AD于点H,交BC于点F.
求证:
(1)OH=OF;
(2)HG=FE.
如图,在□ABCD中,对角线AC,BD相交于点O,过点O作两条直线,分别交AD,BC,AB,CD于点E,F,G,H.求证:四边形EGFH是平行四边形.
答案解析:
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,∠DCO=∠BAO.又∵∠AOE=∠COF,∴△AOE≌△COF(ASA).
∴OE=OF.又∵OB=OD,
∴四边形BFDE是平行四边形.
D
证明:∵AB∥CE,∴∠ADE=∠CED.
在△AOD和△COE中,
∠ADO=∠CEO,
∠AOD=∠COE,
OA=OC,
∴△AOD≌△COE(AAS).
∴OD=OE.
又∵OA=OC,
∴四边形ADCE是平行四边形.
1-8
DBCCCBBD
9.8
10.25
11.证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
又∵E,F分别是OA,OC的中点,
∴EO=AO,FO=CO.
∴EO=FO.
又∵BO=DO,∴四边形BFDE为平行四边形.
12.证明:∵∠A=∠ABC=90°,
∴BC∥AF.
∴∠CBE=∠DFE.
∵E是CD的中点,
∴CE=DE.
在△BEC和△FED中,
∴△BEC≌△FED(AAS).
∴BE=FE.
又∵CE=DE,
∴四边形BDFC是平行四边形.
证明:如答图,连接AC交BD于点O.
∵DC∥AB,DC=AB,
∴四边形ABCD是平行四边形.
∴OA=OC,OB=OD.
又∵DE=FB,
∴OE=OF.
∴四边形AFCE是平行四边形.
∴∠ECF=∠FAE.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,OD=OB.
∴∠ADO=∠CBO,∠DHO=∠BFO.
又∵OD=OB,∴△DHO≌△BFO(AAS).
∴OH=OF.
(2)连接HE,GF,如答图.
答图∵E,G分别是OA,OC的中点,且OA=OC,
∴OG=OE.
又由(1)知,OH=OF,
∴四边形HGFE是平行四边形.
∴HG=FE.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AD∥BC.∴∠AEO=∠CFO.
∴△AEO≌△CFO(AAS).∴EO=FO.
同理可得△BGO≌△DHO(ASA).∴GO=HO.
∴四边形EGFH是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
