5.4 平移(第1课时)
图片预览









文档简介
(共44张PPT)
第五章 相交线与平行线
5.4 平移(1)
重庆市开县西街中学 罗堂喜
请观察课件中几组美丽的图案.⑴它们有什么共同的特点?⑵能否根据每幅图中的一部分绘制出整幅图案?
一、感知图形
图片欣赏
问题:
在滑梯过程中,小朋友身体各部分的运动方向相同吗?运动距离呢?
这些图形的运动过程与小朋友滑滑梯的运动过程,是否有共同点?若有是什么?
二、平移的探究
议一议:
在传送带上,如果货物箱上的A点向左移动50cm ,其他部位会向什么方向移动?移动了多少距离呢?
A
如果小狗向前移动了50米,那么拖着的箱子向什么方向移动?移动了多少距离?
如果小狗向左跑了80cm,那么箱子向 移动了 。
根据上述分析,你能说明什么样的图形运动称为平
移吗?
通过以上的观察,你认为我们应从哪几个方面来说明平移?
移动方向 移动的距离
想一想
平移没有改变图形的形状和大小。
一个图形整体沿着某一直线方向移动,得到一个新的图形,在移动过程中,原图形上的所有的点都向同一个方向运动,且运动相等的距离,这样的图形移动叫做图形的平移变换,简称平移。
特征:
平移的概念
思考:图形平移的方向一定是水平的吗?
说明
图形的平移不一定是水平的,也不一定是竖直的。
如左图的鸟
的飞行也是平移
理性提升
平移有哪些性质?
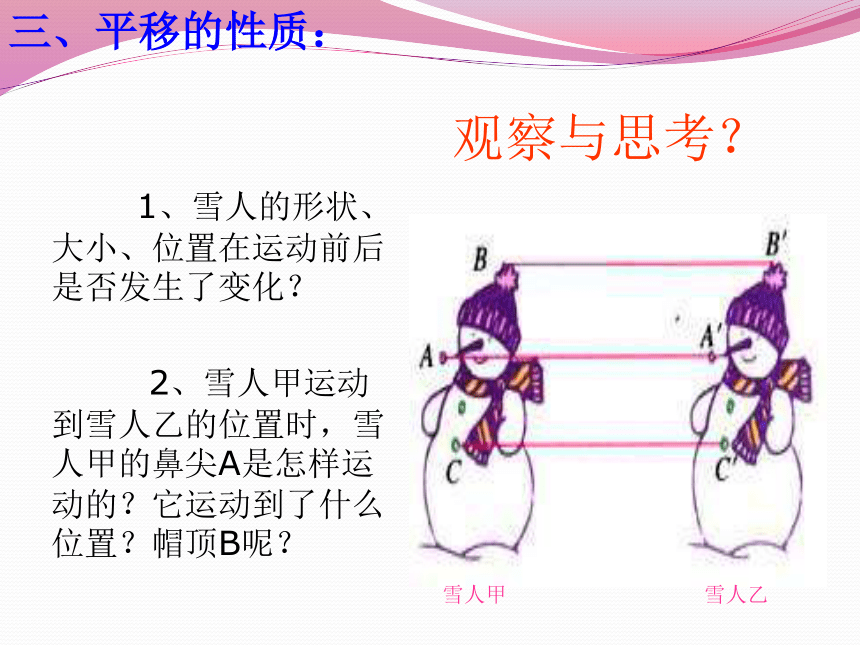
雪人甲
雪人乙
观察与思考?
1、雪人的形状、大小、位置在运动前后是否发生了变化?
2、雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
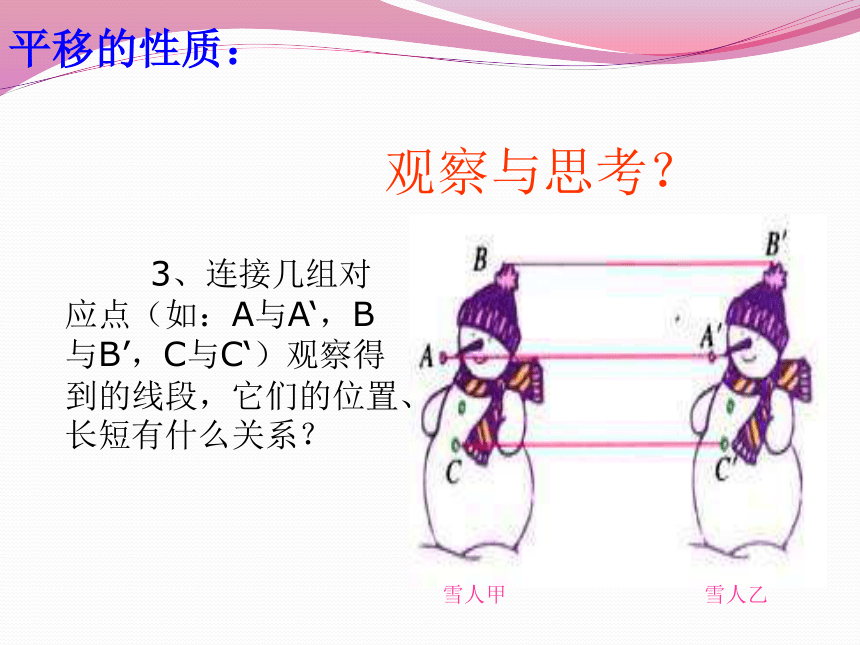
三、平移的性质:
雪人甲
雪人乙
观察与思考?
3、连接几组对应点(如:A与A‘,B与B’,C与C‘)观察得到的线段,它们的位置、长短有什么关系?
平移的性质:
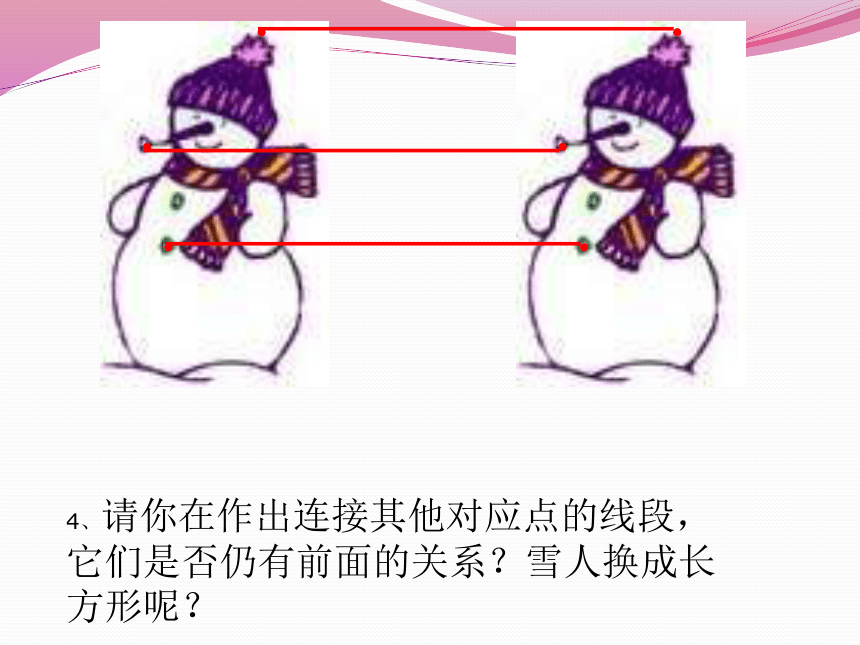
4、请你在作出连接其他对应点的线段,它们是否仍有前面的关系?雪人换成长方形呢?
如果把移动前后的同一台电视机的屏幕分别记做四边形ABCD和四边形EFGH,那么四边形ABCD和四边形EFGH的形状、大小是否相同?
A
B
C
D
E
F
G
H
(1)四边形ABCD经平移变换后得到四边形EFGH,那么它们的形状、大小是否改变?
(2)图中点A经平移到了点E,则点A和点E是一对对应点,你能在图中找出其他各对对应点吗?
(3)请连结各对对应点得出线段,这些线段之间有什么关系呢?
议一议:
A
B
C
D
E
F
G
H
平移的性质
平移变换不改变图形的形状、大小;连结对应点的线段平行且相等。
平移变换不改变图形的形状、大小,这意味着平移前后两图形具有怎样的图形关系?
能完全重合
1、下图中的变换属于平移的有哪些?
F
A
B
D
E
C
随堂练习
2、下图中的变换属于平移的有哪些?
3、下图中,图形(2)可以通过图形(1)平移得到吗?
(1)
(2)
(不考虑颜色)
4、下面这几种物体的运动中,哪些是在平移?
说一说: 请举出现实生活中平移的一些例子。
同学们每天骑自行车沿着笔直的公路来学校上学.
合作交流
在公路上跑着的汽车,天上飞着的飞机.
在笔直的火车路上的火车来来回回的开着
看清这只豹在奔跑中的变化
合作交流
合作交流
解释生活中的现象
装饰工人在墙上用同一个模具刷制图案时,常常每刷制一个图案后移动一次模具,最后形成一幅漂亮的图案。图中任意两个图案之间有何关系?
学以致用
1、 下面两个图形的变换是不是平移?请说明理由。
2、 “小小竹排水中游,巍巍青山两岸走”,所蕴涵的图形变换是__________变换。
3、在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
当堂测试
5、如图所示,是小李家电视机的背景墙面上的装饰板,它是一块底色为蓝色的正方形板,边长18cm, 上面横竖各两道红条进行装饰,红条宽都是2cm,问蓝色部分板面面积是多少?
4、将面积为30cm2的直角三角形ABC向下平移20cm,得到△MNP,则△MNP是 三角形,它的面积是 cm2.
6、下图可以看做是什么“基本图形”通过平移得到的?
观察下列图形,你
能找出基本图案吗?
7、仔细观察下列美丽的图案,回答问题:
(1)这些图案有什么共同特点?
(2)下面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的?
8、在下图中左图是一种“工”字形的砖,右图是怎样通过左图得到的?
9、在下图中,左图是一个正六边形,它经过怎样的平移能得到右图?自己动手做做看,你能得到右图的图案吗?
中考链接
B
(2010四川凉山)下列图案中,只要用其中一部分平移一次就可以得到的是( )
A B C D
经过平移,对应点所连的线段平行且相等; 对应线段平行且相等,对应角相等。
由一个图形改变为另一个图形,在改变过程中,原图形上的所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移。
1、平移的概念:
2、平移的特征:
3、平移的性质:
平移只改变图形的位置,没有改变图形的形状和大小。
小结归纳
图案欣赏:
简单图形经过平移,可以形成复杂而漂亮的图案。
再现情境
图案欣赏:
一个长方形竹园长20米,宽12米,竹园有一条横向宽度都为1.5米的小径(如图).你能求出这个竹园中竹子的种植面积吗(除去小径的面积)?请说明理由.
拓展探究
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
D
A
C
B
E
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
F
D
A
C
B
E
对应顶点:
点D和点C,
点A和点B,
点E和点F.
AD=BC, AE=BF, DE=CF
对应边:
例2 如图所示,已知正方形的边长为4 cm,把它沿AB方向平移3 cm,求平移后两个正方形重叠部分的面积.
D
A
C
B
E
F
解:
S=BC×BF
=4×1
=4(cm2).
BF=4-3=1(cm).
测评题:
1.如图所示,线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3).
(1)线段上所有的点都是沿_____ 移动,并且移动的距离都 .
因此,线段AB,A1B1,A2B2,A3B3的位置关系_______;线段AB,A1B1,A2B2,A3B3的数量关系___________.
(2)在平移变换中,连接各组对应点的线段之间的位置关系是
;数量关系是 .
l1,l2
相等
平行
相等
平行
相等
测评题:
2.如图所示,将三角形ABC平移到三角形A’B’C’ .
在这个平移中:
(1)三角形的整体沿 移动,得到三角形A’B’C’ .三角形A’B’C’与三角形ABC的 和 完全相同.
(2)连接各组对应点的线段即AA’、BB’、CC’之间的数量关系是__________________;位置关系是__________________.
AA’
形状
大小
相等
平行
教科书:
第30页习题5.4 第1、2、3、4题.
第五章 相交线与平行线
5.4 平移(1)
重庆市开县西街中学 罗堂喜
请观察课件中几组美丽的图案.⑴它们有什么共同的特点?⑵能否根据每幅图中的一部分绘制出整幅图案?
一、感知图形
图片欣赏
问题:
在滑梯过程中,小朋友身体各部分的运动方向相同吗?运动距离呢?
这些图形的运动过程与小朋友滑滑梯的运动过程,是否有共同点?若有是什么?
二、平移的探究
议一议:
在传送带上,如果货物箱上的A点向左移动50cm ,其他部位会向什么方向移动?移动了多少距离呢?
A
如果小狗向前移动了50米,那么拖着的箱子向什么方向移动?移动了多少距离?
如果小狗向左跑了80cm,那么箱子向 移动了 。
根据上述分析,你能说明什么样的图形运动称为平
移吗?
通过以上的观察,你认为我们应从哪几个方面来说明平移?
移动方向 移动的距离
想一想
平移没有改变图形的形状和大小。
一个图形整体沿着某一直线方向移动,得到一个新的图形,在移动过程中,原图形上的所有的点都向同一个方向运动,且运动相等的距离,这样的图形移动叫做图形的平移变换,简称平移。
特征:
平移的概念
思考:图形平移的方向一定是水平的吗?
说明
图形的平移不一定是水平的,也不一定是竖直的。
如左图的鸟
的飞行也是平移
理性提升
平移有哪些性质?
雪人甲
雪人乙
观察与思考?
1、雪人的形状、大小、位置在运动前后是否发生了变化?
2、雪人甲运动到雪人乙的位置时,雪人甲的鼻尖A是怎样运动的?它运动到了什么位置?帽顶B呢?
三、平移的性质:
雪人甲
雪人乙
观察与思考?
3、连接几组对应点(如:A与A‘,B与B’,C与C‘)观察得到的线段,它们的位置、长短有什么关系?
平移的性质:
4、请你在作出连接其他对应点的线段,它们是否仍有前面的关系?雪人换成长方形呢?
如果把移动前后的同一台电视机的屏幕分别记做四边形ABCD和四边形EFGH,那么四边形ABCD和四边形EFGH的形状、大小是否相同?
A
B
C
D
E
F
G
H
(1)四边形ABCD经平移变换后得到四边形EFGH,那么它们的形状、大小是否改变?
(2)图中点A经平移到了点E,则点A和点E是一对对应点,你能在图中找出其他各对对应点吗?
(3)请连结各对对应点得出线段,这些线段之间有什么关系呢?
议一议:
A
B
C
D
E
F
G
H
平移的性质
平移变换不改变图形的形状、大小;连结对应点的线段平行且相等。
平移变换不改变图形的形状、大小,这意味着平移前后两图形具有怎样的图形关系?
能完全重合
1、下图中的变换属于平移的有哪些?
F
A
B
D
E
C
随堂练习
2、下图中的变换属于平移的有哪些?
3、下图中,图形(2)可以通过图形(1)平移得到吗?
(1)
(2)
(不考虑颜色)
4、下面这几种物体的运动中,哪些是在平移?
说一说: 请举出现实生活中平移的一些例子。
同学们每天骑自行车沿着笔直的公路来学校上学.
合作交流
在公路上跑着的汽车,天上飞着的飞机.
在笔直的火车路上的火车来来回回的开着
看清这只豹在奔跑中的变化
合作交流
合作交流
解释生活中的现象
装饰工人在墙上用同一个模具刷制图案时,常常每刷制一个图案后移动一次模具,最后形成一幅漂亮的图案。图中任意两个图案之间有何关系?
学以致用
1、 下面两个图形的变换是不是平移?请说明理由。
2、 “小小竹排水中游,巍巍青山两岸走”,所蕴涵的图形变换是__________变换。
3、在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
当堂测试
5、如图所示,是小李家电视机的背景墙面上的装饰板,它是一块底色为蓝色的正方形板,边长18cm, 上面横竖各两道红条进行装饰,红条宽都是2cm,问蓝色部分板面面积是多少?
4、将面积为30cm2的直角三角形ABC向下平移20cm,得到△MNP,则△MNP是 三角形,它的面积是 cm2.
6、下图可以看做是什么“基本图形”通过平移得到的?
观察下列图形,你
能找出基本图案吗?
7、仔细观察下列美丽的图案,回答问题:
(1)这些图案有什么共同特点?
(2)下面这些图案能否根据其中一部分绘制整个图案?若能,你能否想象出是怎么绘制的?
8、在下图中左图是一种“工”字形的砖,右图是怎样通过左图得到的?
9、在下图中,左图是一个正六边形,它经过怎样的平移能得到右图?自己动手做做看,你能得到右图的图案吗?
中考链接
B
(2010四川凉山)下列图案中,只要用其中一部分平移一次就可以得到的是( )
A B C D
经过平移,对应点所连的线段平行且相等; 对应线段平行且相等,对应角相等。
由一个图形改变为另一个图形,在改变过程中,原图形上的所有的点都向同一个方向运动,且运动相等的距离,这样的图形改变叫做图形的平移变换,简称平移。
1、平移的概念:
2、平移的特征:
3、平移的性质:
平移只改变图形的位置,没有改变图形的形状和大小。
小结归纳
图案欣赏:
简单图形经过平移,可以形成复杂而漂亮的图案。
再现情境
图案欣赏:
一个长方形竹园长20米,宽12米,竹园有一条横向宽度都为1.5米的小径(如图).你能求出这个竹园中竹子的种植面积吗(除去小径的面积)?请说明理由.
拓展探究
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
D
A
C
B
E
例1 如图,AB∥CD,AD∥BC,DE⊥AB于E点.将三角DAE形平移,得到三角形CBF.
⑴请画出平移后的三角形CBF .
⑵写出平移前后的对应顶点和对应相等的边.
F
D
A
C
B
E
对应顶点:
点D和点C,
点A和点B,
点E和点F.
AD=BC, AE=BF, DE=CF
对应边:
例2 如图所示,已知正方形的边长为4 cm,把它沿AB方向平移3 cm,求平移后两个正方形重叠部分的面积.
D
A
C
B
E
F
解:
S=BC×BF
=4×1
=4(cm2).
BF=4-3=1(cm).
测评题:
1.如图所示,线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3).
(1)线段上所有的点都是沿_____ 移动,并且移动的距离都 .
因此,线段AB,A1B1,A2B2,A3B3的位置关系_______;线段AB,A1B1,A2B2,A3B3的数量关系___________.
(2)在平移变换中,连接各组对应点的线段之间的位置关系是
;数量关系是 .
l1,l2
相等
平行
相等
平行
相等
测评题:
2.如图所示,将三角形ABC平移到三角形A’B’C’ .
在这个平移中:
(1)三角形的整体沿 移动,得到三角形A’B’C’ .三角形A’B’C’与三角形ABC的 和 完全相同.
(2)连接各组对应点的线段即AA’、BB’、CC’之间的数量关系是__________________;位置关系是__________________.
AA’
形状
大小
相等
平行
教科书:
第30页习题5.4 第1、2、3、4题.
