8.1成对数据的统计相关性 同步训练B-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析)
文档属性
| 名称 | 8.1成对数据的统计相关性 同步训练B-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 796.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 19:24:26 | ||
图片预览


文档简介
8.1成对数据的统计相关性B
一.选择题(共8小题)
1.如图是根据变量,的观测数据,,2,3,,得到的散点图,由这些散点图可以判断变量,具有相关关系的图是
A.①② B.②③ C.③④ D.①④
2.在各散点图中,两个变量具有正相关关系的是
A. B.
C. D.
3.两个变量的相关关系有①正相关,②负相关,③不相关,则下列散点图从左到右分别反映的变量间的相关关系是
A.①②③ B.②③① C.②①③ D.①③②
4.甲、乙、丙、丁四位同学各自对,两变量的线性相关性做试验,并用回归分析方法分别求得相关系数如表:
甲 乙 丙 丁
则哪位同学的试验结果体现,两变量有更强的线性相关性
A.甲 B.乙 C.丙 D.丁
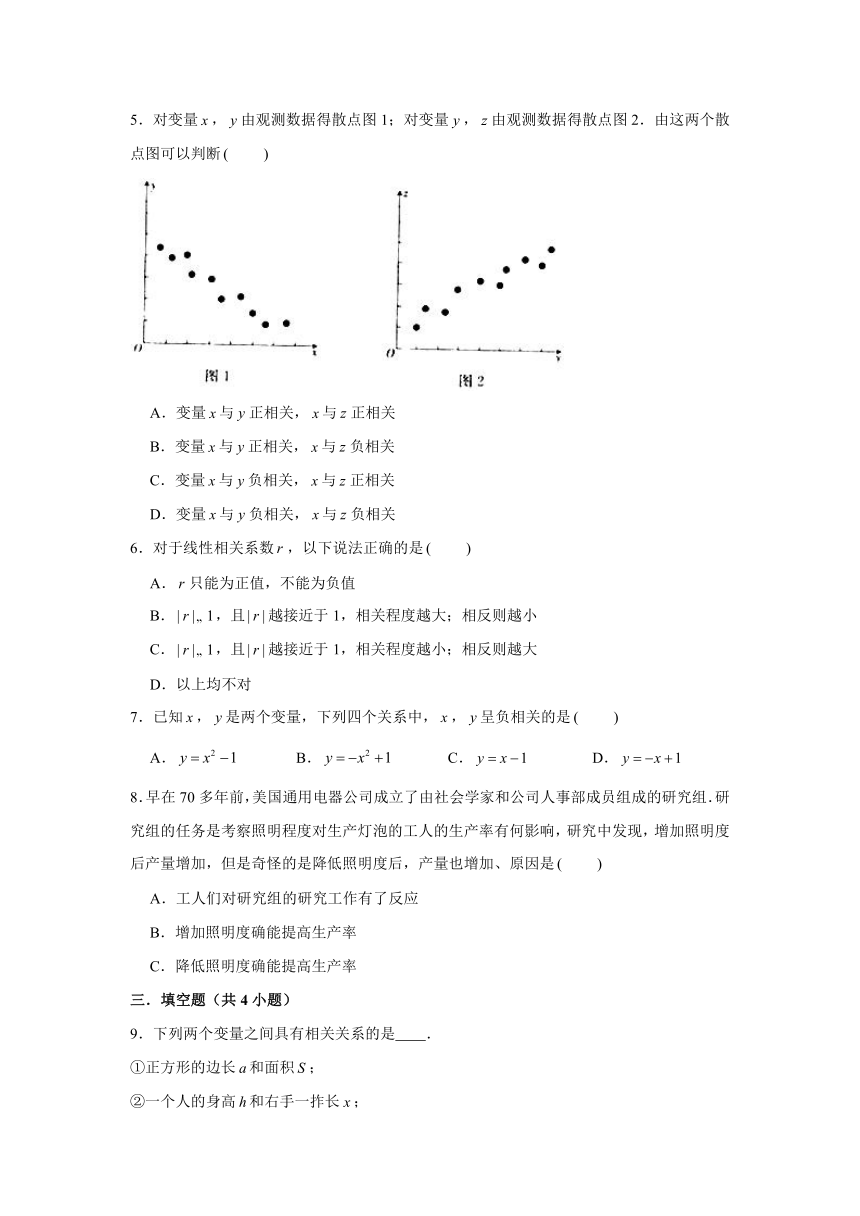
5.对变量,由观测数据得散点图1;对变量,由观测数据得散点图2.由这两个散点图可以判断
A.变量与正相关,与正相关
B.变量与正相关,与负相关
C.变量与负相关,与正相关
D.变量与负相关,与负相关
6.对于线性相关系数,以下说法正确的是
A.只能为正值,不能为负值
B.,且越接近于1,相关程度越大;相反则越小
C.,且越接近于1,相关程度越小;相反则越大
D.以上均不对
7.已知,是两个变量,下列四个关系中,,呈负相关的是
A. B. C. D.
8.早在70多年前,美国通用电器公司成立了由社会学家和公司人事部成员组成的研究组.研究组的任务是考察照明程度对生产灯泡的工人的生产率有何影响,研究中发现,增加照明度后产量增加,但是奇怪的是降低照明度后,产量也增加、原因是
A.工人们对研究组的研究工作有了反应
B.增加照明度确能提高生产率
C.降低照明度确能提高生产率
三.填空题(共4小题)
9.下列两个变量之间具有相关关系的是 .
①正方形的边长和面积;
②一个人的身高和右手一拃长;
③真空中的自由落体运动其下落的距离和下落的时间;
④一个人的身高和体重.
10.下列两个变量之间的关系:
①角度和它的余弦值;
②正边形的边数与内角和;
③家庭的支出与收入;
④某户家庭用电量与电价间的关系.
其中是相关关系的有 .
11.有下列关系:①人的年龄与他(她拥有的财富之间的关系; ②曲线上的点与该点的坐标之间的关系; ③苹果的产量与气候之间的关系;④森林中的同一种树木,其横断面直径与高度之间的关系,其中是相关关系的为 .
12.用线性回归模型求得甲、乙、丙3组不同的数据的线性相关系数分别为0.81,,0.63,其中 (填甲、乙、丙中的一个)组数据的线性相关性最强.
四.解答题(共4小题)
13.举例说明:现实生活中存在两个变量间的相关关系.
14.已知,之间的一组数据如表:
(1)分别从集合,3,6,7,8,,2,3,4,5中各取一个数,,求的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为与,试根据残差平方和:的大小,判断哪条直线拟合程度更好.
15.为了对某班考试成绩进行分析,现从全班同学中随机抽取8位同学,他们的数学、物理成绩对应如表.根据表中数据分析:是否有的把握认为,变量与具有线性相关关系?
学生编号 1 2 3 4 5 6 7 8
数学分数 60 65 70 75 80 85 90 95
无理分数 72 77 80 85 88 90 93 95
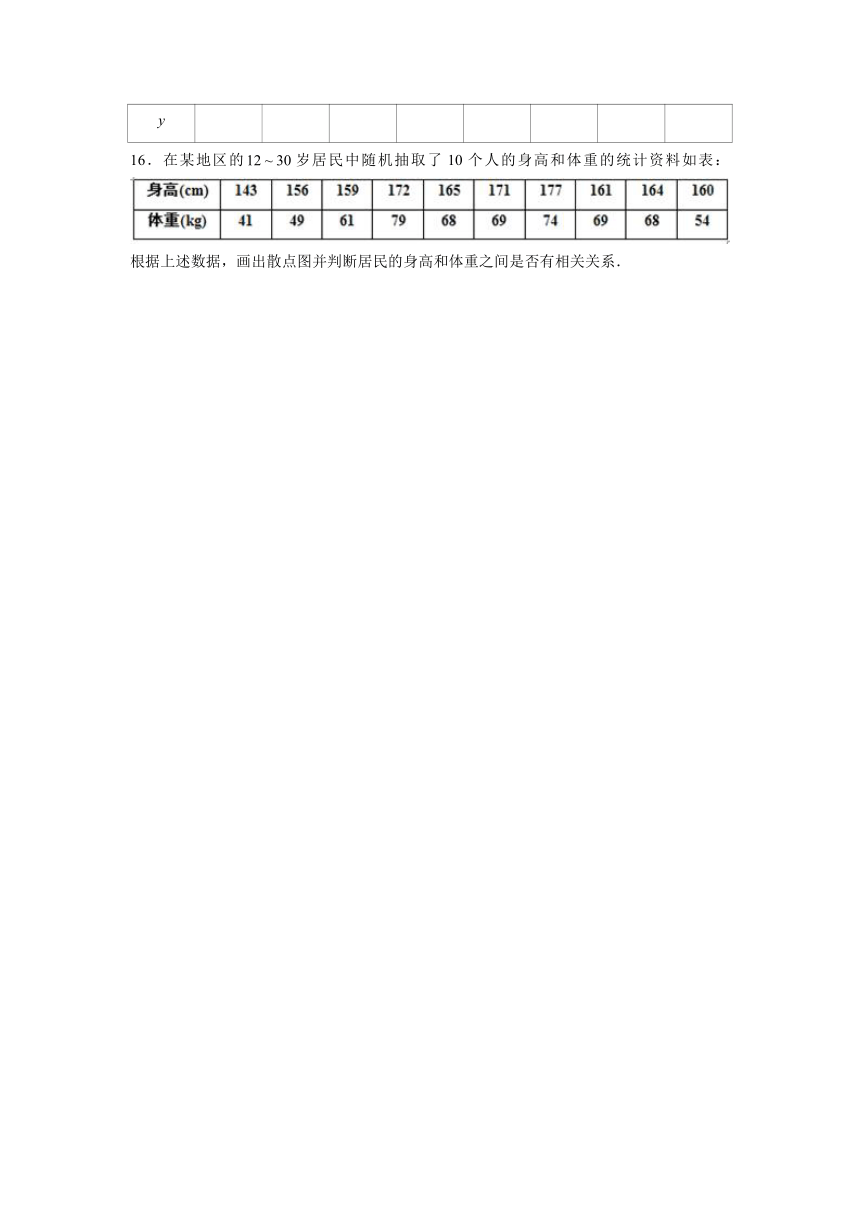
16.在某地区的岁居民中随机抽取了10个人的身高和体重的统计资料如表:
根据上述数据,画出散点图并判断居民的身高和体重之间是否有相关关系.
8.1成对数据的统计相关性B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由图③知,变量随的增大而减小,各点整体呈下降趋势,与有明显的负相关关系,
由图④知,变量随的增大而增大,各点整体呈上升趋势,与有明显的正相关关系.
故选:.
2.【解答】解:根据题意,依次分析选项为:
对于、是相关关系,但不是正相关关系,不符合题意;
对于、是相关关系,也是正相关关系,符合题意;
对于、是相关关系,是负相关关系,不符合题意;
对于、所示的散点图中,样本点不成带状分布,这两个变量不具有线性相关关系,不符合题意.
故选:.
3.【解答】解:对于(1),图中的点成带状分布,且从左到右上升,是正相关关系①;
对于(2),图中的点没有明显的带状分布,是不相关的③;
对于(3),图中的点成带状分布,且从左到右是下降的,是负相关关系②.
故选:.
4.【解答】解:在验证两个变量之间的线性相关关系中,相关指数的绝对值越接近于1,相关性越强,
四个选项中丁的相关指数绝对值最大,
所以,甲的试验结果体现、两变量有更强的线性相关性.
故选:.
5.【解答】解:由这两个散点图可以判断,变量与负相关,与正相关,则与负相关.
故选:.
6.【解答】解:因为线性相关有正相关和负相关,所以对应的线性相关系数,也有正和负,相关系数的取值范围是,,所以错误.
两个变量之间的相关系数,的绝对值越接近于1,表现两个变量的线性相关性越强,相反则越小,所以正确,对应错误.
故选:.
7.【解答】解:根据题意,依次分析选项:
对于,,当增大时,的值不一定减小,两个变量不是负相关,不符合题意;
对于,,当增大时,的值不一定减小,两个变量不是负相关,不符合题意;
对于,,当增大时,的值一定增大,两个变量正相关,不符合题意;
对于,,当增大时,的值一定减小,两个变量负相关,符合题意;
故选:.
8.【解答】解:研究中发现,增加照明度后产量增加,降低照明度后,产量也增加;
原因是“工人们对研究组的研究工作有了反应”.
故选:.
三.填空题(共4小题)
9.【解答】解:对于①,正方形的边长和面积是函数关系,不是相关关系;
对于②,一般情况下,一个人的身高和右手一拃长是正相关关系;
对于③,真空中的自由落体运动其下落的距离和下落的时间是函数关系,不是相关关系;
对于④,一般情况下,一个人的身高和他的体重是正相关关系.
故选:②④.
10.【解答】解:①角度和它的余弦值是函数关系,因为任意一个角总对应唯一的一个余弦值;
②正边形的边数与内角和为:正边形的内角和(正边形的边数,它是函数关系;
③家庭的支出与收入有关,但不是唯一因素,所以它们是相关关系;
④某户家庭用电量与电价间的关系为:电价家庭用电量电的单价,它是函数关系,不是相关关系.
故答案为:③.
11.【解答】解:对于①,一般地,人的年龄与他(她拥有的财富是一种相关关系;
对于②,曲线上的点与该点的坐标,是一种函数关系;
对于③,苹果的产量与气候之间的关系,是一种相关关系;
对于④,森林中的同一种树木,其横断面直径与高度之间的关系,是相关关系.
故答案为:①③④.
12.【解答】解:两个变量与的回归模型中,它们的相关指数越接近于1,
这个模型的拟合效果就越好,
在甲、乙、丙中,所给的数值中0.98是相关指数最大的值,
即乙的拟合效果最好.
故答案为:乙.
四.解答题(共4小题)
13.【解答】解:现实生活中存在大量的相关关系例如:
①商品销售收入与广告费支出之间的关系,商品销售收入与广告费用支出有着密切的联系,但商品销售收入不仅和广告费用支出有关,还和商品质量,居民收入等因素有关.
②粮食产量与施肥量之间的关系,在一定范围内,施肥量越大,粮食产量就越高,但施肥量并不是决定粮食产量的唯一因素,还与土壤质量,降雨量,田间管理水平因素有关.
14.【解答】解:(1)由题意知这是一个古典概型,
试验发生包含的所有事件是分别从集合,中各取一个数组成数对,共有25对,
其中满足的有,,,,,,,,,共9对
故使的概率为.
(2)用作为拟合直线时,所得的实际值与的估计值的差的平方和为:.
用作为拟合直线时,所得的实际值与的估计值的差的平方和为:.
,
故用直线拟合程度更好.
15.【解答】解:,
.
,,.
所以线性相关系数.
所以有把握认为变量与具有线性相关关系.
16.【解答】解:以轴表示身高,轴表示体重,
可得到相应的散点图如图所示,
由散点图可知,两者之间具有相关关系,且为正相关.
一.选择题(共8小题)
1.如图是根据变量,的观测数据,,2,3,,得到的散点图,由这些散点图可以判断变量,具有相关关系的图是
A.①② B.②③ C.③④ D.①④
2.在各散点图中,两个变量具有正相关关系的是
A. B.
C. D.
3.两个变量的相关关系有①正相关,②负相关,③不相关,则下列散点图从左到右分别反映的变量间的相关关系是
A.①②③ B.②③① C.②①③ D.①③②
4.甲、乙、丙、丁四位同学各自对,两变量的线性相关性做试验,并用回归分析方法分别求得相关系数如表:
甲 乙 丙 丁
则哪位同学的试验结果体现,两变量有更强的线性相关性
A.甲 B.乙 C.丙 D.丁
5.对变量,由观测数据得散点图1;对变量,由观测数据得散点图2.由这两个散点图可以判断
A.变量与正相关,与正相关
B.变量与正相关,与负相关
C.变量与负相关,与正相关
D.变量与负相关,与负相关
6.对于线性相关系数,以下说法正确的是
A.只能为正值,不能为负值
B.,且越接近于1,相关程度越大;相反则越小
C.,且越接近于1,相关程度越小;相反则越大
D.以上均不对
7.已知,是两个变量,下列四个关系中,,呈负相关的是
A. B. C. D.
8.早在70多年前,美国通用电器公司成立了由社会学家和公司人事部成员组成的研究组.研究组的任务是考察照明程度对生产灯泡的工人的生产率有何影响,研究中发现,增加照明度后产量增加,但是奇怪的是降低照明度后,产量也增加、原因是
A.工人们对研究组的研究工作有了反应
B.增加照明度确能提高生产率
C.降低照明度确能提高生产率
三.填空题(共4小题)
9.下列两个变量之间具有相关关系的是 .
①正方形的边长和面积;
②一个人的身高和右手一拃长;
③真空中的自由落体运动其下落的距离和下落的时间;
④一个人的身高和体重.
10.下列两个变量之间的关系:
①角度和它的余弦值;
②正边形的边数与内角和;
③家庭的支出与收入;
④某户家庭用电量与电价间的关系.
其中是相关关系的有 .
11.有下列关系:①人的年龄与他(她拥有的财富之间的关系; ②曲线上的点与该点的坐标之间的关系; ③苹果的产量与气候之间的关系;④森林中的同一种树木,其横断面直径与高度之间的关系,其中是相关关系的为 .
12.用线性回归模型求得甲、乙、丙3组不同的数据的线性相关系数分别为0.81,,0.63,其中 (填甲、乙、丙中的一个)组数据的线性相关性最强.
四.解答题(共4小题)
13.举例说明:现实生活中存在两个变量间的相关关系.
14.已知,之间的一组数据如表:
(1)分别从集合,3,6,7,8,,2,3,4,5中各取一个数,,求的概率;
(2)对于表中数据,甲、乙两同学给出的拟合直线分别为与,试根据残差平方和:的大小,判断哪条直线拟合程度更好.
15.为了对某班考试成绩进行分析,现从全班同学中随机抽取8位同学,他们的数学、物理成绩对应如表.根据表中数据分析:是否有的把握认为,变量与具有线性相关关系?
学生编号 1 2 3 4 5 6 7 8
数学分数 60 65 70 75 80 85 90 95
无理分数 72 77 80 85 88 90 93 95
16.在某地区的岁居民中随机抽取了10个人的身高和体重的统计资料如表:
根据上述数据,画出散点图并判断居民的身高和体重之间是否有相关关系.
8.1成对数据的统计相关性B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由图③知,变量随的增大而减小,各点整体呈下降趋势,与有明显的负相关关系,
由图④知,变量随的增大而增大,各点整体呈上升趋势,与有明显的正相关关系.
故选:.
2.【解答】解:根据题意,依次分析选项为:
对于、是相关关系,但不是正相关关系,不符合题意;
对于、是相关关系,也是正相关关系,符合题意;
对于、是相关关系,是负相关关系,不符合题意;
对于、所示的散点图中,样本点不成带状分布,这两个变量不具有线性相关关系,不符合题意.
故选:.
3.【解答】解:对于(1),图中的点成带状分布,且从左到右上升,是正相关关系①;
对于(2),图中的点没有明显的带状分布,是不相关的③;
对于(3),图中的点成带状分布,且从左到右是下降的,是负相关关系②.
故选:.
4.【解答】解:在验证两个变量之间的线性相关关系中,相关指数的绝对值越接近于1,相关性越强,
四个选项中丁的相关指数绝对值最大,
所以,甲的试验结果体现、两变量有更强的线性相关性.
故选:.
5.【解答】解:由这两个散点图可以判断,变量与负相关,与正相关,则与负相关.
故选:.
6.【解答】解:因为线性相关有正相关和负相关,所以对应的线性相关系数,也有正和负,相关系数的取值范围是,,所以错误.
两个变量之间的相关系数,的绝对值越接近于1,表现两个变量的线性相关性越强,相反则越小,所以正确,对应错误.
故选:.
7.【解答】解:根据题意,依次分析选项:
对于,,当增大时,的值不一定减小,两个变量不是负相关,不符合题意;
对于,,当增大时,的值不一定减小,两个变量不是负相关,不符合题意;
对于,,当增大时,的值一定增大,两个变量正相关,不符合题意;
对于,,当增大时,的值一定减小,两个变量负相关,符合题意;
故选:.
8.【解答】解:研究中发现,增加照明度后产量增加,降低照明度后,产量也增加;
原因是“工人们对研究组的研究工作有了反应”.
故选:.
三.填空题(共4小题)
9.【解答】解:对于①,正方形的边长和面积是函数关系,不是相关关系;
对于②,一般情况下,一个人的身高和右手一拃长是正相关关系;
对于③,真空中的自由落体运动其下落的距离和下落的时间是函数关系,不是相关关系;
对于④,一般情况下,一个人的身高和他的体重是正相关关系.
故选:②④.
10.【解答】解:①角度和它的余弦值是函数关系,因为任意一个角总对应唯一的一个余弦值;
②正边形的边数与内角和为:正边形的内角和(正边形的边数,它是函数关系;
③家庭的支出与收入有关,但不是唯一因素,所以它们是相关关系;
④某户家庭用电量与电价间的关系为:电价家庭用电量电的单价,它是函数关系,不是相关关系.
故答案为:③.
11.【解答】解:对于①,一般地,人的年龄与他(她拥有的财富是一种相关关系;
对于②,曲线上的点与该点的坐标,是一种函数关系;
对于③,苹果的产量与气候之间的关系,是一种相关关系;
对于④,森林中的同一种树木,其横断面直径与高度之间的关系,是相关关系.
故答案为:①③④.
12.【解答】解:两个变量与的回归模型中,它们的相关指数越接近于1,
这个模型的拟合效果就越好,
在甲、乙、丙中,所给的数值中0.98是相关指数最大的值,
即乙的拟合效果最好.
故答案为:乙.
四.解答题(共4小题)
13.【解答】解:现实生活中存在大量的相关关系例如:
①商品销售收入与广告费支出之间的关系,商品销售收入与广告费用支出有着密切的联系,但商品销售收入不仅和广告费用支出有关,还和商品质量,居民收入等因素有关.
②粮食产量与施肥量之间的关系,在一定范围内,施肥量越大,粮食产量就越高,但施肥量并不是决定粮食产量的唯一因素,还与土壤质量,降雨量,田间管理水平因素有关.
14.【解答】解:(1)由题意知这是一个古典概型,
试验发生包含的所有事件是分别从集合,中各取一个数组成数对,共有25对,
其中满足的有,,,,,,,,,共9对
故使的概率为.
(2)用作为拟合直线时,所得的实际值与的估计值的差的平方和为:.
用作为拟合直线时,所得的实际值与的估计值的差的平方和为:.
,
故用直线拟合程度更好.
15.【解答】解:,
.
,,.
所以线性相关系数.
所以有把握认为变量与具有线性相关关系.
16.【解答】解:以轴表示身高,轴表示体重,
可得到相应的散点图如图所示,
由散点图可知,两者之间具有相关关系,且为正相关.
