8.2一元线性回归模型及其应用 同步训练B-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析)
文档属性
| 名称 | 8.2一元线性回归模型及其应用 同步训练B-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 19:25:05 | ||
图片预览




文档简介
8.2一元线性回归模型及其应用B
一.选择题(共8小题)
1.已知与之间的一组数据
0 1 2 3
1 3 5 7
则与的线性回归方程必过点
A.,2 B. 1, C.,4 D.,
2.根据如下样本数据:
1 2 3 4 5 6
5 4.5 3.5 3 2.5 2
得到的线性回归方程为,则
A., B., C., D.,
3.已知回归方程,则该方程在样本处的残差为
A. B.1 C.2 D.5
4.根据散点图,对两个具有非线性关系的相关变量,进行回归分析,设,,利用最小二乘法,得到线性回归方程为,则变量的最大值的估计值是
A. B. C. D.
5.某科研型企业,每年都对应聘入围的大学生进行体检,其中一项重要指标就是身高与体重比,其中每年入围大学生体重(单位:与身高(单位:基本都具有线性相关关系,根据今年的一组样本数据,,2,,,用最小二乘法建立的回归方程为,则下列结论中不正确的是
A.与具有正的线性相关关系
B.回归直线过样本点的中心,
C.若某应聘大学生身高增加,则其体重约增加
D.若某应聘大学生身高为,则可断定其体重必为
6.在一组样本数据,,,,,,,,,,不全相等)的散点图中,若所有样本点,,2,,都在直线上,则这组样本数据的样本相关系数为
A. B.1 C. D.
7.在一项调查中有两个变量和,如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为关于的回归方程的函数类型是
A. B.
C. D.
8.广告投入对商品的销售额有较大影响,某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元)
广告费 2 3 4 5 6
销售额 29 41 50 59 71
由上表可得回归方程为,又已知生产该商品的成本(不含广告费)为(单位:万元),据此模型预测最大的纯利润为
A.30.15万元 B.21.00万元 C.19.00万元 D.10.50万元
二.多选题(共2小题)
9.研究变量,得到一组样本数据,进行回归分析,以下说法正确的是
A.残差平方和越小的模型,拟合的效果越好
B.用相关指数来刻画回归效果,越小说明拟合效果越好
C.在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位
D.若变量和之间的相关系数为,则变量和之间的负相关很强.
三.填空题(共4小题)
10.已知与之间的一组数据如表所示:
0 1 2 3
1 3
当变化时,回归直线必经过定点 .
11.已知具有相关关系的两个变量,的一组观测数据如表所示,若据此利用最小二乘估计得到回归方程,则 .
3 4 5 6
2.5
4 4.5
12.某单位为了了解用电量与气温之间的关系,随机统计了某4天的用电量与当天的气温,并制作了对照表:
气温 20 16 12 4
用电量(度 14 28 44 62
由表中数据得到回归直线方程,则预测当气温为时,用电量的度数是 .
13.已知与之间的一组数据:
1 3 5 7
7 9
已求得关于与的线性回归方程,则的值为 .
四.解答题(共4小题)
14.自新冠肺炎疫情爆发以来,国内外数学专家纷纷利用数学模型对新冠病毒的可能感染规模和传播风险等进行预测,为疫情防控作出数据指导.某同学从国家卫健委获取了2020年1月20日至2020年1月25日全国累计报告确诊病例数据,如表:
日期 1月20日 1月21日 1月22日 1月23日 1月24日 1月25日
时间(天 1 2 3 4 5 6
确诊数(人 291 440 571 830 1287 1975
其中,,.
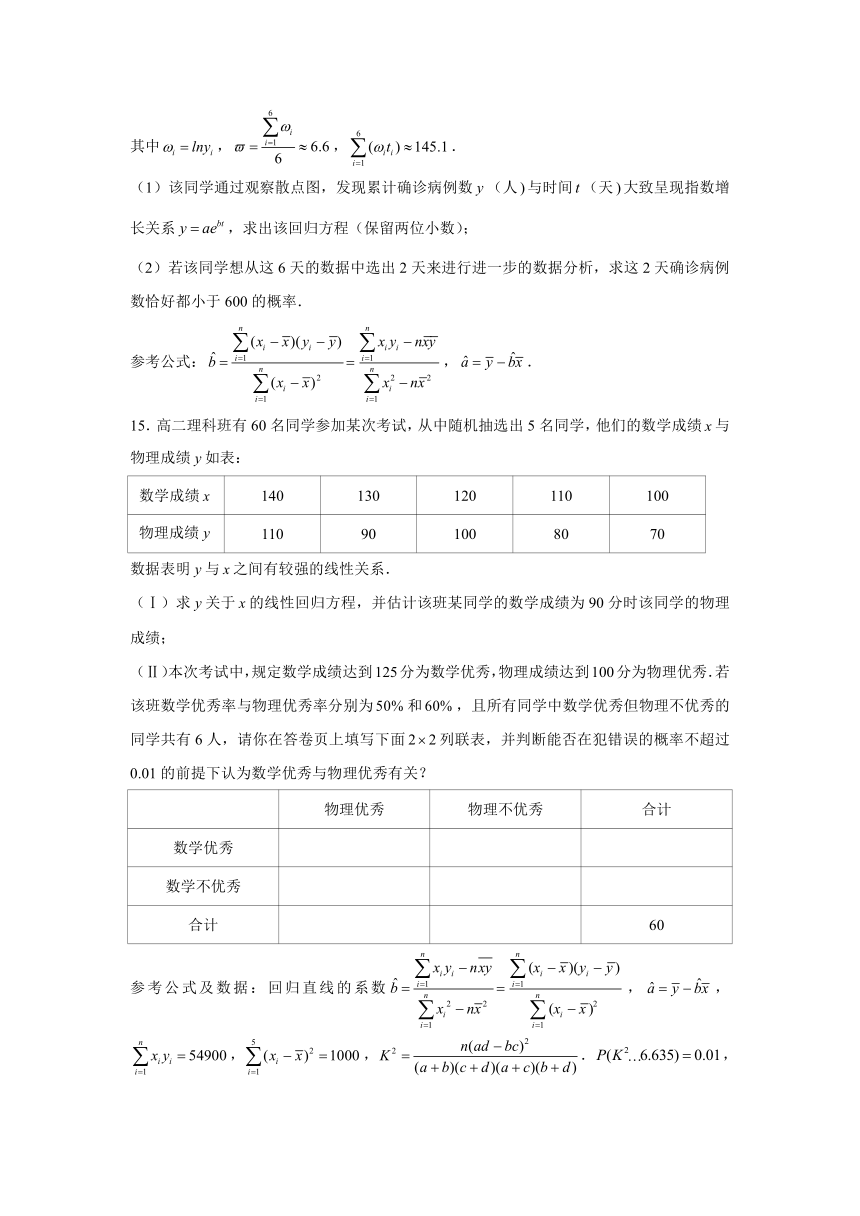
(1)该同学通过观察散点图,发现累计确诊病例数(人与时间(天大致呈现指数增长关系,求出该回归方程(保留两位小数);
(2)若该同学想从这6天的数据中选出2天来进行进一步的数据分析,求这2天确诊病例数恰好都小于600的概率.
参考公式:,.
15.高二理科班有60名同学参加某次考试,从中随机抽选出5名同学,他们的数学成绩与物理成绩如表:
数学成绩 140 130 120 110 100
物理成绩 110 90 100 80 70
数据表明与之间有较强的线性关系.
(Ⅰ)求关于的线性回归方程,并估计该班某同学的数学成绩为90分时该同学的物理成绩;
(Ⅱ)本次考试中,规定数学成绩达到125分为数学优秀,物理成绩达到100分为物理优秀.若该班数学优秀率与物理优秀率分别为和,且所有同学中数学优秀但物理不优秀的同学共有6人,请你在答卷页上填写下面列联表,并判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关?
物理优秀 物理不优秀 合计
数学优秀
数学不优秀
合计
60
参考公式及数据:回归直线的系数,,,,.,.
16.为了了解某校高中生的身体质量情况,某调查机构进行了一次高一学生体重和身高的抽样调查,从中抽取了8名学生(编号为的身高和体重数据.如表:
学生的编号 1 2 3 4 5 6 7 8
身高 164 176 165 163 170 172 168 182
体重 60 72 77 54
72 55
某调查机构分析发现学生的身高和体重之间有较强的线性相关关系,在编号为6的体检数据丢失之前,调查员甲已进行相关的数据分析并计算出该组数据的线性回归方程为,且根据回归方程预估一名身高为的学生体重为,计算得到的其他数据如下:.
(1)求的值及表格中8名学生体重的平均值;
(2)在数据处理时,调查员乙发现编号为8的学生体重数据有误,应为,身高数据无误.请你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为的学生的体重.
附:回归直线方程的斜率和截距的最小二乘法估计分别为:,.
17.某单位共有10名员工,他们某年的收入如表:
员工编号 1 2 3 4 5 6 7 8 9 10
年薪(万元) 4 4.5 6 5 6.5 7.5 8 8.5 9 51
(1)求该单位员工当年年薪的平均值和中位数;
(2)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第六年的年薪为多少?
附:线性回归方程中系数计算公式分别为:,其中、为样本均值.
8.2一元线性回归模型及其应用B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由表格可得,,.
样本中心点为,
则线性回归方程必过点,4 .
故选:.
2.【解答】解:【方法一】根据表中数据,计算,
;
计算;
.
【方法二】根据表中样本数据知,变量随的增大而减小,
所以线性回归方程中,;
又,对应,所以.
故选:.
3.【解答】解:当时,,
方程在样本处的残差是.
故选:.
4.【解答】解:由题意可知,,
所以,
所以.
故选:.
5.【解答】解:由于线性回归方程中的系数为0.83,因此与具有正的线性相关关系,所以正确;
因为线性回归方程必过样本中心点,所以正确;
由线性回归方程中系数的意义知,每增加,其体重约增加,所以正确;
当某大学生的身高为时,其体重估计值是,而不是具体值,所以错误.
故选:.
6.【解答】解:这组样本数据的所有样本点,,2,,都在直线上,
这组样本数据完全相关,
即说明这组数据的样本完全负相关,其相关系数是.
故选:.
7.【解答】解:由散点图可得,图象是抛物线形状,
符合作为关于的回归方程类型的是.
故选:.
8.【解答】解:由表中数据,计算,
,
代入回归方程中,得,
所以,
计算纯利润为,
当且仅当时取“”,
所以据此模型预测最大的纯利润为19.
故选:.
二.多选题(共2小题)
9.【解答】解:残差平方和越小的模型,拟合的效果越好,故正确;
用相关指数来刻画回归效果,越大说明拟合效果越好,故错误;
在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位,故正确;
若变量和之间的相关系数为,接近,则变量和之间的负相关很强,故正确.
故选:.
三.填空题(共4小题)
10.【解答】解:由题意可得;
,
由回归直线方程的性质可知,回归直线必经过定点是样本中心,.
故答案为:,.
11.【解答】解:由题意可知,
,
因为回归直线经过样本中心,
所以,
解得.
故答案为:3.
12.【解答】解:由题意,,,
关于的线性回归方程为,
根据线性回归方程必过样本的中心,
,
.
关于的线性回归方程为.
当气温为时,.
故答案为:70.
13.【解答】解:由题意可得,因为回归直线,经过样本中心,所以,
所以,解得,
故答案为:2.
四.解答题(共4小题)
14.【解答】解:(1)由题意,指数增长关系,
两边取为底的对数,可得,
令,
则,其样本中心点;
根据表中数据得:,
由
则,
所以该回归方程为.
(2)设6天的数据为,,,,,,
所有可能为:,,,,,,,,,,,,
,,,共15种,
选出2天都小于600的,,,
故得这2天确诊病例数恰好都小于600的概率为.
15.【解答】解:(Ⅰ),
.
,
.
关于的线性回归方程为,
取,得.
估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;
(Ⅱ)由题意填写列联表:
物理优秀 物理不优秀 合计
数学优秀 24 6 30
数学不优秀 12 18 30
合计 36 24 60
,
能在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关.
16.【解答】解:(1)调查员由线性回归方程,
预估一名身高为的学生体重为,
由此可计算,
故.
(2)由(1)知更正前的数据.
由,
得,
更正后的数据,
,,,
故.
更正后该组数据的线性回归方程为.
当身高为时,体重为
故一名身高为的学生的体重预估为.
17.【解答】解:(1)该单位员工当年年薪的平均值为万元,
中位数为万元;
(2)设,,2,3,分别表示工作年限及相应年薪,
则,,,
,
,.
线性回归方程:.
取,得.
可预测该员工年后的年薪收入为10.9万元.
一.选择题(共8小题)
1.已知与之间的一组数据
0 1 2 3
1 3 5 7
则与的线性回归方程必过点
A.,2 B. 1, C.,4 D.,
2.根据如下样本数据:
1 2 3 4 5 6
5 4.5 3.5 3 2.5 2
得到的线性回归方程为,则
A., B., C., D.,
3.已知回归方程,则该方程在样本处的残差为
A. B.1 C.2 D.5
4.根据散点图,对两个具有非线性关系的相关变量,进行回归分析,设,,利用最小二乘法,得到线性回归方程为,则变量的最大值的估计值是
A. B. C. D.
5.某科研型企业,每年都对应聘入围的大学生进行体检,其中一项重要指标就是身高与体重比,其中每年入围大学生体重(单位:与身高(单位:基本都具有线性相关关系,根据今年的一组样本数据,,2,,,用最小二乘法建立的回归方程为,则下列结论中不正确的是
A.与具有正的线性相关关系
B.回归直线过样本点的中心,
C.若某应聘大学生身高增加,则其体重约增加
D.若某应聘大学生身高为,则可断定其体重必为
6.在一组样本数据,,,,,,,,,,不全相等)的散点图中,若所有样本点,,2,,都在直线上,则这组样本数据的样本相关系数为
A. B.1 C. D.
7.在一项调查中有两个变量和,如图是由这两个变量近8年来的取值数据得到的散点图,那么适宜作为关于的回归方程的函数类型是
A. B.
C. D.
8.广告投入对商品的销售额有较大影响,某电商对连续5个年度的广告费和销售额进行统计,得到统计数据如表(单位:万元)
广告费 2 3 4 5 6
销售额 29 41 50 59 71
由上表可得回归方程为,又已知生产该商品的成本(不含广告费)为(单位:万元),据此模型预测最大的纯利润为
A.30.15万元 B.21.00万元 C.19.00万元 D.10.50万元
二.多选题(共2小题)
9.研究变量,得到一组样本数据,进行回归分析,以下说法正确的是
A.残差平方和越小的模型,拟合的效果越好
B.用相关指数来刻画回归效果,越小说明拟合效果越好
C.在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位
D.若变量和之间的相关系数为,则变量和之间的负相关很强.
三.填空题(共4小题)
10.已知与之间的一组数据如表所示:
0 1 2 3
1 3
当变化时,回归直线必经过定点 .
11.已知具有相关关系的两个变量,的一组观测数据如表所示,若据此利用最小二乘估计得到回归方程,则 .
3 4 5 6
2.5
4 4.5
12.某单位为了了解用电量与气温之间的关系,随机统计了某4天的用电量与当天的气温,并制作了对照表:
气温 20 16 12 4
用电量(度 14 28 44 62
由表中数据得到回归直线方程,则预测当气温为时,用电量的度数是 .
13.已知与之间的一组数据:
1 3 5 7
7 9
已求得关于与的线性回归方程,则的值为 .
四.解答题(共4小题)
14.自新冠肺炎疫情爆发以来,国内外数学专家纷纷利用数学模型对新冠病毒的可能感染规模和传播风险等进行预测,为疫情防控作出数据指导.某同学从国家卫健委获取了2020年1月20日至2020年1月25日全国累计报告确诊病例数据,如表:
日期 1月20日 1月21日 1月22日 1月23日 1月24日 1月25日
时间(天 1 2 3 4 5 6
确诊数(人 291 440 571 830 1287 1975
其中,,.
(1)该同学通过观察散点图,发现累计确诊病例数(人与时间(天大致呈现指数增长关系,求出该回归方程(保留两位小数);
(2)若该同学想从这6天的数据中选出2天来进行进一步的数据分析,求这2天确诊病例数恰好都小于600的概率.
参考公式:,.
15.高二理科班有60名同学参加某次考试,从中随机抽选出5名同学,他们的数学成绩与物理成绩如表:
数学成绩 140 130 120 110 100
物理成绩 110 90 100 80 70
数据表明与之间有较强的线性关系.
(Ⅰ)求关于的线性回归方程,并估计该班某同学的数学成绩为90分时该同学的物理成绩;
(Ⅱ)本次考试中,规定数学成绩达到125分为数学优秀,物理成绩达到100分为物理优秀.若该班数学优秀率与物理优秀率分别为和,且所有同学中数学优秀但物理不优秀的同学共有6人,请你在答卷页上填写下面列联表,并判断能否在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关?
物理优秀 物理不优秀 合计
数学优秀
数学不优秀
合计
60
参考公式及数据:回归直线的系数,,,,.,.
16.为了了解某校高中生的身体质量情况,某调查机构进行了一次高一学生体重和身高的抽样调查,从中抽取了8名学生(编号为的身高和体重数据.如表:
学生的编号 1 2 3 4 5 6 7 8
身高 164 176 165 163 170 172 168 182
体重 60 72 77 54
72 55
某调查机构分析发现学生的身高和体重之间有较强的线性相关关系,在编号为6的体检数据丢失之前,调查员甲已进行相关的数据分析并计算出该组数据的线性回归方程为,且根据回归方程预估一名身高为的学生体重为,计算得到的其他数据如下:.
(1)求的值及表格中8名学生体重的平均值;
(2)在数据处理时,调查员乙发现编号为8的学生体重数据有误,应为,身高数据无误.请你根据调查员乙更正的数据重新计算线性回归方程,并据此预估一名身高为的学生的体重.
附:回归直线方程的斜率和截距的最小二乘法估计分别为:,.
17.某单位共有10名员工,他们某年的收入如表:
员工编号 1 2 3 4 5 6 7 8 9 10
年薪(万元) 4 4.5 6 5 6.5 7.5 8 8.5 9 51
(1)求该单位员工当年年薪的平均值和中位数;
(2)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元、5.5万元、6万元、8.5万元,预测该员工第六年的年薪为多少?
附:线性回归方程中系数计算公式分别为:,其中、为样本均值.
8.2一元线性回归模型及其应用B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由表格可得,,.
样本中心点为,
则线性回归方程必过点,4 .
故选:.
2.【解答】解:【方法一】根据表中数据,计算,
;
计算;
.
【方法二】根据表中样本数据知,变量随的增大而减小,
所以线性回归方程中,;
又,对应,所以.
故选:.
3.【解答】解:当时,,
方程在样本处的残差是.
故选:.
4.【解答】解:由题意可知,,
所以,
所以.
故选:.
5.【解答】解:由于线性回归方程中的系数为0.83,因此与具有正的线性相关关系,所以正确;
因为线性回归方程必过样本中心点,所以正确;
由线性回归方程中系数的意义知,每增加,其体重约增加,所以正确;
当某大学生的身高为时,其体重估计值是,而不是具体值,所以错误.
故选:.
6.【解答】解:这组样本数据的所有样本点,,2,,都在直线上,
这组样本数据完全相关,
即说明这组数据的样本完全负相关,其相关系数是.
故选:.
7.【解答】解:由散点图可得,图象是抛物线形状,
符合作为关于的回归方程类型的是.
故选:.
8.【解答】解:由表中数据,计算,
,
代入回归方程中,得,
所以,
计算纯利润为,
当且仅当时取“”,
所以据此模型预测最大的纯利润为19.
故选:.
二.多选题(共2小题)
9.【解答】解:残差平方和越小的模型,拟合的效果越好,故正确;
用相关指数来刻画回归效果,越大说明拟合效果越好,故错误;
在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加0.2个单位,故正确;
若变量和之间的相关系数为,接近,则变量和之间的负相关很强,故正确.
故选:.
三.填空题(共4小题)
10.【解答】解:由题意可得;
,
由回归直线方程的性质可知,回归直线必经过定点是样本中心,.
故答案为:,.
11.【解答】解:由题意可知,
,
因为回归直线经过样本中心,
所以,
解得.
故答案为:3.
12.【解答】解:由题意,,,
关于的线性回归方程为,
根据线性回归方程必过样本的中心,
,
.
关于的线性回归方程为.
当气温为时,.
故答案为:70.
13.【解答】解:由题意可得,因为回归直线,经过样本中心,所以,
所以,解得,
故答案为:2.
四.解答题(共4小题)
14.【解答】解:(1)由题意,指数增长关系,
两边取为底的对数,可得,
令,
则,其样本中心点;
根据表中数据得:,
由
则,
所以该回归方程为.
(2)设6天的数据为,,,,,,
所有可能为:,,,,,,,,,,,,
,,,共15种,
选出2天都小于600的,,,
故得这2天确诊病例数恰好都小于600的概率为.
15.【解答】解:(Ⅰ),
.
,
.
关于的线性回归方程为,
取,得.
估计该班某同学的数学成绩为90分时该同学的物理成绩为63分;
(Ⅱ)由题意填写列联表:
物理优秀 物理不优秀 合计
数学优秀 24 6 30
数学不优秀 12 18 30
合计 36 24 60
,
能在犯错误的概率不超过0.01的前提下认为数学优秀与物理优秀有关.
16.【解答】解:(1)调查员由线性回归方程,
预估一名身高为的学生体重为,
由此可计算,
故.
(2)由(1)知更正前的数据.
由,
得,
更正后的数据,
,,,
故.
更正后该组数据的线性回归方程为.
当身高为时,体重为
故一名身高为的学生的体重预估为.
17.【解答】解:(1)该单位员工当年年薪的平均值为万元,
中位数为万元;
(2)设,,2,3,分别表示工作年限及相应年薪,
则,,,
,
,.
线性回归方程:.
取,得.
可预测该员工年后的年薪收入为10.9万元.
