8.3列联表和独立性检验 同步训练A-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析)
文档属性
| 名称 | 8.3列联表和独立性检验 同步训练A-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册(Word含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览




文档简介
8.3列联表和独立性检验A
一.选择题(共8小题)
1.根据下面的列联表得到如下四个判断:
①至少有的把握认为“患肝病与嗜酒有关”;②至少有的把握认为“患肝病与嗜酒有关”;③在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”;④在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”.
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
其中正确命题的个数为
A.0 B.1 C.2 D.3
2.为了调查患胃病是否与生活不规律有关,在患胃病与生活不规律这两个分类变量的计算中,下列说法正确的是
A.越大,“患胃病与生活不规律没有关系”的可信程度越大.
B.越大,“患胃病与生活不规律有关系”的可信程度越小.
C.若计算得,经查临界值表知,则在100个生活不规律的人中必有95人患胃病.
D.从统计量中得知有的把握认为患胃病与生活不规律有关,是指有的可能性使得推断出现错误.
3.如果根据性别与是否爱好运动的列联表得到,所以判断性别与运动有关,那么这种判断犯错的可能性不超过
0.050 0.010 0.001
3.841 6.635 10.828
A. B. C. D.
4.通过随机询问150名大学生是否参加某社团活动,得到如表的列联表:
男 女
参加 55 25
不参加 30 40
总计 85 65
0.05 0.010 0.001
3.841 6.635 10.828
参照如表,得到的正确的结论是
A.在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别无关”
B.在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别有关”
C.有以上的把握认为“是否参加该社团活动与性别有关”
D.有以上的把握认为“是否参加该社团活动与性别无关”
5.假设两个分类变量和,他们的取值分别为,和,,其样本频数列联表如表:
总计
总计
对于以下数据,对同一样本说明与有关的可能性最大的一组是
A.,,, B.,,,
C.,,, D.,,,
6.某生物研究所在新冠病毒疫苗的研制过程中,为验证疫苗的治疗效果,进行了动物的对比试验,现对200只小白鼠进行试验,得到如表数据:
未发病 发病 合计
未接种疫苗 20 60 80
接种疫苗 80 40 120
合计 100 100 200
附:.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
则下列说法正确的是
A.至少有的把握认为“发病与没接种疫苗有关“
B.至多有的把握认为“发病与没接种疫苗有关”
C.至多有的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有
7.2020年12月30日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病.2021年1月3日,北京市人民政府新闻办公室召开疫情防控第200场例行新闻发布会,表示不在岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的110人进行了临床试验,得到如下列联表:
能接种 不能接种 总计
岁内 40 20 60
岁外 20 30 50
总计 60 50 110
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
参照附表,得到的正确结论是
A.在犯错误的概率不超过的前提下,认为“能接种与年龄段无关”
B.在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”
C.有以上的把握认为“能接种与年龄段无关”
D.有以上的把握认为“能接种与年龄段有关”
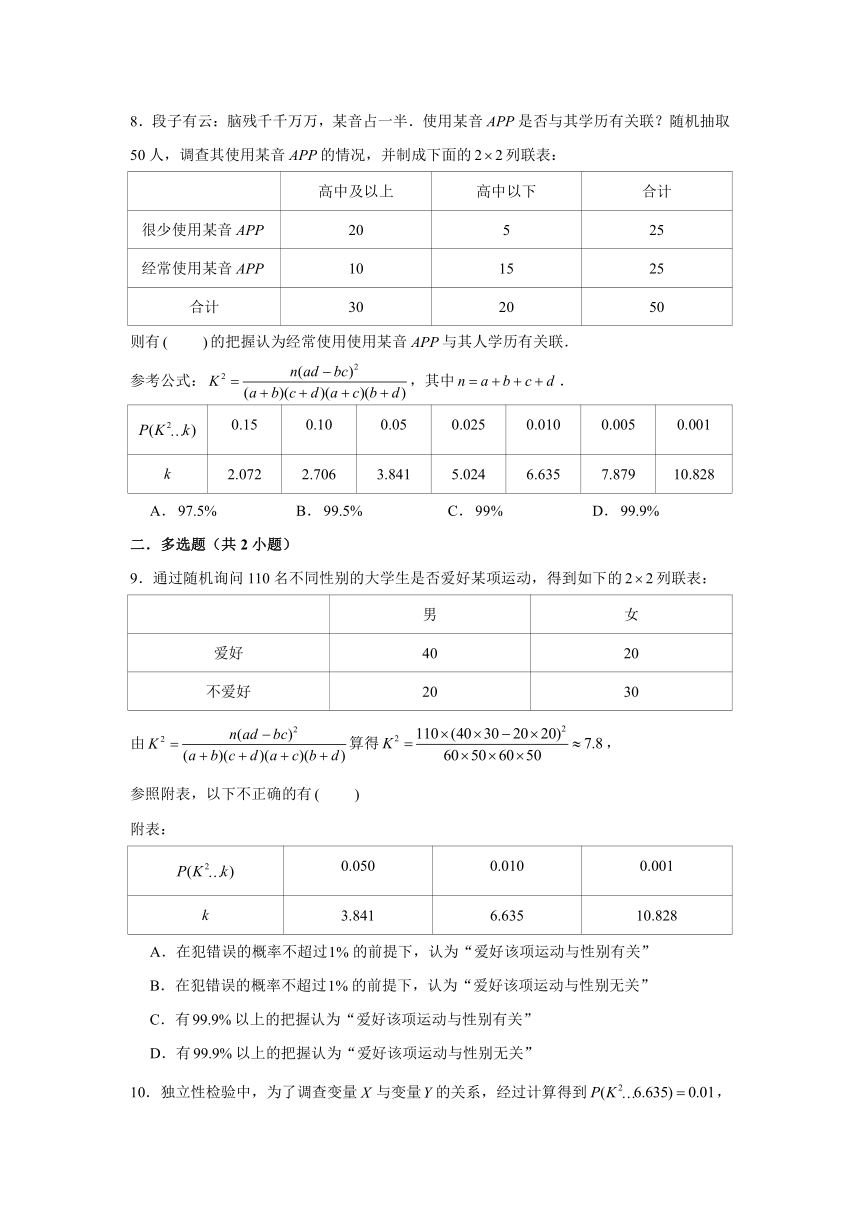
8.段子有云:脑残千千万万,某音占一半.使用某音是否与其学历有关联?随机抽取50人,调查其使用某音的情况,并制成下面的列联表:
高中及以上 高中以下 合计
很少使用某音 20 5 25
经常使用某音 10 15 25
合计 30 20 50
则有 的把握认为经常使用使用某音与其人学历有关联.
参考公式:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
A. B. C. D.
二.多选题(共2小题)
9.通过随机询问110名不同性别的大学生是否爱好某项运动,得到如下的列联表:
男 女
爱好 40 20
不爱好 20 30
由算得,
参照附表,以下不正确的有
附表:
0.050 0.010 0.001
3.841 6.635 10.828
A.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”
C.有以上的把握认为“爱好该项运动与性别有关”
D.有以上的把握认为“爱好该项运动与性别无关”
10.独立性检验中,为了调查变量与变量的关系,经过计算得到,表示的意义是
A.有的把握认为变量与变量没有关系
B.有的把握认为变量与变量有关系
C.有的把握认为变量与变量有关系
D.有的把握认为变量与变量没有关系
三.填空题(共4小题)
11.某手机运营商为了拓展业务,现对该手机使用潜在客户进行调查,随机抽取国内国外潜在用户代表各100名,调查用户对是否使用该手机的态度,得到如图所示的等高条形图.根据等高图, (填“有”或“没有” 以上的把握认为持乐观态度和国内外差异有关.
(参考公式与数据:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
12.已知变量,,由它们的样本数据计算得到的观测值,的部分临界值表如表:
0.10 0.05 0.025 0.010 0.005
2.706 3.841 5.024 6.635 7.879
则最大有 的把握说变量,有关系.(填百分数)
13.某高校有10000名学生,其中女生3000名,男生7000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的列表如表,则 .(用数字作答)
男 女 合计
爱好体育运动
9
不爱好体育运动 28
合计
120
14.如表是不完整的列联表,其中,,则 .
总计
55
总计
120
四.解答题(共4小题)
15.今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占.
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上
40
50岁以下
合计 10
100
(1)请将下面的列联表补充完整,并判断是否有的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁以上的概率.
参考表:
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,其中.
16.“中国式过马路”存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下的列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是.
(Ⅰ)求列联表中的,的值;
男性 女性 合计
反感 10
不反感
8
合计
30
(Ⅱ)根据列联表中的数据,判断是否有把握认为反感“中国式过马路”与性别有关?
临界值表:
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635
参考公式:,.
17.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如表所示(单位:人)
80及80分以 80分以下 总计
试验班 35 15 50
对照班 20
50
总计 55 45
参考公式:
0.025 0.010 0.005 0.001
5.024 6.635 7.879 10.828
(1)求,;
(2)能否在犯错误的概率不超过0.005的情况下认为教学方式与成绩有关系?
18.为了比较两种治疗失眠症的药(分别称为药,药)的疗效,某机构随机地选取20位患者服用药,20位患者服用药,观察这40位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:,以整数部分当茎,小数部分当叶,绘制了如图茎叶图:
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这40名患者日平均增加睡眠时间的中位数,并将日平均增加睡眠时间超过和不超过的患者人数填入如表的列联表:
超过 不超过
服用药
服用药
(3)根据(2)中的列联表,能否有的把握认为,两种药的疗效有差异?
附:.
0.01 0.005 0.001
6.635 7.879 10.828
8.3列联表和独立性检验A
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由列联表中数据可求得随机变量的观测值,
所以在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关系”,即至少有的把握认为“患肝病与嗜酒有关系”.因此②③正确,
故选:.
2.【解答】解:在独立性检验中,越大,“患胃病与生活不规律有关系”的可信程度越大,所以错误、错误;
计算得时,经查临界值表知,不是指在100个生活不规律的人中必有95人患胃病,所以错误;
从统计量中得知有的把握认为患胃病与生活不规律有关,是指有的可能性使得推断出现错误,所以正确.
故选:.
3.【解答】解:根据性别与是否爱好运动的列联表得到,
所以有的把握说明性别与运动有关,
即有的出错可能性.
故选:.
4.【解答】解:根据题意补充列联表为:
男 女 总计
参加 55 25 80
不参加 30 40 70
合计 85 65 150
根据表中数据,计算,
所以有以上的把握认为“是否参加该社团活动与性别有关”,
即在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别有关”.
故选:.
5.【解答】解:根据独立性检验原理知,越大,说明与有关的可能性越大;
选项中,;
选项中,;
选项中,;
选项中,;
所以选项中与有关的可能性最大.
故选:.
6.【解答】解:根据所给表格的数据,结合计算公式,
可得其观测值为,
所以至少有的把握认为“发病与没接种疫苗有关”.
故选:.
7.【解答】解:根据列联表中数据,计算,
参照附表知,在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”,
即有以上的把握认为“能接种与年龄段有关”.
故选:.
8.【解答】解:由表可知,,
所以有的把握认为他们之间有关联.
故选:.
二.多选题(共2小题)
9.【解答】解:由列联表计算,
参照附表知,,
所以在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”, 正确,错误;
即有以上的把握认为“爱好该项运动与性别有关”,
且没有以上的把握认为“爱好该项运动与性别有关”,
也没有以上的把握认为“爱好该项运动与性别无关”,所以、错误.
故选:.
10.【解答】解:独立性检验中,由,
它表示的意义是:有的把握认为变量与变量没有关系,正确;
即有的把握认为变量与变量有关系,正确.
故选:.
三.填空题(共4小题)
11.【解答】解:由题填写列联表如下,
乐观 不乐观 总计
国内代表 60 40 100
国外代表 40 60 100
总计 100 100 200
,
所以有以上的把握认为持乐观态度和国内外差异有关.
故答案为:有.
12.【解答】解:由样本数据计算得到的观测值,
且,
所以最大有的把握说变量,有关系.
故答案为:.
13.【解答】解:根据分层抽样原理,计算抽取男生(人,
女生(人,
所以(人,
(人,
所以(人.
故答案为:29.
14.【解答】解:由题意得,
解得,
故答案为:15.
四.解答题(共4小题)
15.【解答】解:(1)由题意可知
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 6 34 40
50岁以下 4 56 60
合计 10 90 100
,
所以没有的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,
可知抽取的5人中,有3人是50岁以上的,2人是50岁以下的,
随机抽取3人恰有2人是50岁以上的概率.
16.【解答】解:(Ⅰ)在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是,
,解得,
又,解得.
故,.
(Ⅱ)补充完整的列联表如下所示,
男性 女性 合计
反感 10 8 18
不反感 4 8 12
合计 14 16 30
,
故没有把握认为反感“中国式过马路”与性别有关.
17.【解答】解:(1)由列联表知,,
;
(2)由表中数据,计算的观测值为,
因为,
所以能在犯错误的概率不超过0.005的前提下认为教学方式与成绩有关系.
18.【解答】解:(1)四个理由,任意一个均可,(答案不唯一)
①从以上茎叶图可以看出,药疗效的试验结果有的叶集中在茎2和3上,而药疗效的试验结果有的叶集中在茎0和1上,由此可看出药的疗效更好.
②从茎叶图的分布情况可以看出,服用药的患者日平均增加睡眠时间的平均数大于2,而服用药的患者日平均增加睡眠时间的平均数小于2,因此可知药的疗效更好.
③由茎叶图可知,服用药的患者日平均增加睡眠时间的中位数是,而服用药的患者日平均增加睡眠时间的中位数是,因此药的疗效更好.
④由茎叶图可知,服用药的患者日平均增加睡眠时间分布在茎2上的最多,关于茎2大致呈对称分布;而服用药的患者日平均增加睡眠时间分布在茎1上的最多,关于茎1大致呈对称分布;又患者在服用两种药后日平均增加睡眠时间分布的区间相同,故可以认为服用药的患者日平均增加睡眠时间比服用药的患者日平均增加睡眠时间更多,因此药的疗效更好.
(2)由茎叶图可知,40组数据的中位数为,
因此列联表如下:
超过 不超过
服用药 14 6
服用药 5 15
(3)由于;
所以有的把握认为,两种药的疗效有差异.
一.选择题(共8小题)
1.根据下面的列联表得到如下四个判断:
①至少有的把握认为“患肝病与嗜酒有关”;②至少有的把握认为“患肝病与嗜酒有关”;③在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关”;④在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒无关”.
嗜酒 不嗜酒 总计
患肝病 700 60 760
未患肝病 200 32 232
总计 900 92 992
其中正确命题的个数为
A.0 B.1 C.2 D.3
2.为了调查患胃病是否与生活不规律有关,在患胃病与生活不规律这两个分类变量的计算中,下列说法正确的是
A.越大,“患胃病与生活不规律没有关系”的可信程度越大.
B.越大,“患胃病与生活不规律有关系”的可信程度越小.
C.若计算得,经查临界值表知,则在100个生活不规律的人中必有95人患胃病.
D.从统计量中得知有的把握认为患胃病与生活不规律有关,是指有的可能性使得推断出现错误.
3.如果根据性别与是否爱好运动的列联表得到,所以判断性别与运动有关,那么这种判断犯错的可能性不超过
0.050 0.010 0.001
3.841 6.635 10.828
A. B. C. D.
4.通过随机询问150名大学生是否参加某社团活动,得到如表的列联表:
男 女
参加 55 25
不参加 30 40
总计 85 65
0.05 0.010 0.001
3.841 6.635 10.828
参照如表,得到的正确的结论是
A.在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别无关”
B.在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别有关”
C.有以上的把握认为“是否参加该社团活动与性别有关”
D.有以上的把握认为“是否参加该社团活动与性别无关”
5.假设两个分类变量和,他们的取值分别为,和,,其样本频数列联表如表:
总计
总计
对于以下数据,对同一样本说明与有关的可能性最大的一组是
A.,,, B.,,,
C.,,, D.,,,
6.某生物研究所在新冠病毒疫苗的研制过程中,为验证疫苗的治疗效果,进行了动物的对比试验,现对200只小白鼠进行试验,得到如表数据:
未发病 发病 合计
未接种疫苗 20 60 80
接种疫苗 80 40 120
合计 100 100 200
附:.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
则下列说法正确的是
A.至少有的把握认为“发病与没接种疫苗有关“
B.至多有的把握认为“发病与没接种疫苗有关”
C.至多有的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有
7.2020年12月30日,国家药品监督管理局附条件批准国药集团中国生物北京生物制品研究所有限责任公司的新型冠状病毒灭活疫苗细胞)注册申请.该疫苗是首家获批的国产新冠病毒灭活疫苗,适用于预防由新型冠状病毒感染引起的疾病.2021年1月3日,北京市人民政府新闻办公室召开疫情防控第200场例行新闻发布会,表示不在岁接种年龄段范围的人员,需要等待进一步临床试验数据.近日专家对该年龄内和该年龄段外的110人进行了临床试验,得到如下列联表:
能接种 不能接种 总计
岁内 40 20 60
岁外 20 30 50
总计 60 50 110
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
参照附表,得到的正确结论是
A.在犯错误的概率不超过的前提下,认为“能接种与年龄段无关”
B.在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”
C.有以上的把握认为“能接种与年龄段无关”
D.有以上的把握认为“能接种与年龄段有关”
8.段子有云:脑残千千万万,某音占一半.使用某音是否与其学历有关联?随机抽取50人,调查其使用某音的情况,并制成下面的列联表:
高中及以上 高中以下 合计
很少使用某音 20 5 25
经常使用某音 10 15 25
合计 30 20 50
则有 的把握认为经常使用使用某音与其人学历有关联.
参考公式:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
A. B. C. D.
二.多选题(共2小题)
9.通过随机询问110名不同性别的大学生是否爱好某项运动,得到如下的列联表:
男 女
爱好 40 20
不爱好 20 30
由算得,
参照附表,以下不正确的有
附表:
0.050 0.010 0.001
3.841 6.635 10.828
A.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关”
C.有以上的把握认为“爱好该项运动与性别有关”
D.有以上的把握认为“爱好该项运动与性别无关”
10.独立性检验中,为了调查变量与变量的关系,经过计算得到,表示的意义是
A.有的把握认为变量与变量没有关系
B.有的把握认为变量与变量有关系
C.有的把握认为变量与变量有关系
D.有的把握认为变量与变量没有关系
三.填空题(共4小题)
11.某手机运营商为了拓展业务,现对该手机使用潜在客户进行调查,随机抽取国内国外潜在用户代表各100名,调查用户对是否使用该手机的态度,得到如图所示的等高条形图.根据等高图, (填“有”或“没有” 以上的把握认为持乐观态度和国内外差异有关.
(参考公式与数据:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
12.已知变量,,由它们的样本数据计算得到的观测值,的部分临界值表如表:
0.10 0.05 0.025 0.010 0.005
2.706 3.841 5.024 6.635 7.879
则最大有 的把握说变量,有关系.(填百分数)
13.某高校有10000名学生,其中女生3000名,男生7000名.为调查爱好体育运动是否与性别有关,用分层抽样的方法抽取120名学生,制成独立性检验的列表如表,则 .(用数字作答)
男 女 合计
爱好体育运动
9
不爱好体育运动 28
合计
120
14.如表是不完整的列联表,其中,,则 .
总计
55
总计
120
四.解答题(共4小题)
15.今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多,为了严控疫情传播,做好重点人群的预防工作,某地区共统计返乡人员100人,其中50岁及以上的共有40人.这100人中确诊的有10名,其中50岁以下的人占.
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上
40
50岁以下
合计 10
100
(1)请将下面的列联表补充完整,并判断是否有的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,若从这5人中随机抽取3人,求恰有2人为50岁以上的概率.
参考表:
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,其中.
16.“中国式过马路”存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下的列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是.
(Ⅰ)求列联表中的,的值;
男性 女性 合计
反感 10
不反感
8
合计
30
(Ⅱ)根据列联表中的数据,判断是否有把握认为反感“中国式过马路”与性别有关?
临界值表:
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010
0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635
参考公式:,.
17.某校在两个班进行教学方式对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如表所示(单位:人)
80及80分以 80分以下 总计
试验班 35 15 50
对照班 20
50
总计 55 45
参考公式:
0.025 0.010 0.005 0.001
5.024 6.635 7.879 10.828
(1)求,;
(2)能否在犯错误的概率不超过0.005的情况下认为教学方式与成绩有关系?
18.为了比较两种治疗失眠症的药(分别称为药,药)的疗效,某机构随机地选取20位患者服用药,20位患者服用药,观察这40位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:,以整数部分当茎,小数部分当叶,绘制了如图茎叶图:
(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;
(2)求这40名患者日平均增加睡眠时间的中位数,并将日平均增加睡眠时间超过和不超过的患者人数填入如表的列联表:
超过 不超过
服用药
服用药
(3)根据(2)中的列联表,能否有的把握认为,两种药的疗效有差异?
附:.
0.01 0.005 0.001
6.635 7.879 10.828
8.3列联表和独立性检验A
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由列联表中数据可求得随机变量的观测值,
所以在犯错误的概率不超过0.01的前提下认为“患肝病与嗜酒有关系”,即至少有的把握认为“患肝病与嗜酒有关系”.因此②③正确,
故选:.
2.【解答】解:在独立性检验中,越大,“患胃病与生活不规律有关系”的可信程度越大,所以错误、错误;
计算得时,经查临界值表知,不是指在100个生活不规律的人中必有95人患胃病,所以错误;
从统计量中得知有的把握认为患胃病与生活不规律有关,是指有的可能性使得推断出现错误,所以正确.
故选:.
3.【解答】解:根据性别与是否爱好运动的列联表得到,
所以有的把握说明性别与运动有关,
即有的出错可能性.
故选:.
4.【解答】解:根据题意补充列联表为:
男 女 总计
参加 55 25 80
不参加 30 40 70
合计 85 65 150
根据表中数据,计算,
所以有以上的把握认为“是否参加该社团活动与性别有关”,
即在犯错的概率不超过的前提下,认为“是否参加该社团活动与性别有关”.
故选:.
5.【解答】解:根据独立性检验原理知,越大,说明与有关的可能性越大;
选项中,;
选项中,;
选项中,;
选项中,;
所以选项中与有关的可能性最大.
故选:.
6.【解答】解:根据所给表格的数据,结合计算公式,
可得其观测值为,
所以至少有的把握认为“发病与没接种疫苗有关”.
故选:.
7.【解答】解:根据列联表中数据,计算,
参照附表知,在犯错误的概率不超过的前提下,认为“能接种与年龄段有关”,
即有以上的把握认为“能接种与年龄段有关”.
故选:.
8.【解答】解:由表可知,,
所以有的把握认为他们之间有关联.
故选:.
二.多选题(共2小题)
9.【解答】解:由列联表计算,
参照附表知,,
所以在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关”, 正确,错误;
即有以上的把握认为“爱好该项运动与性别有关”,
且没有以上的把握认为“爱好该项运动与性别有关”,
也没有以上的把握认为“爱好该项运动与性别无关”,所以、错误.
故选:.
10.【解答】解:独立性检验中,由,
它表示的意义是:有的把握认为变量与变量没有关系,正确;
即有的把握认为变量与变量有关系,正确.
故选:.
三.填空题(共4小题)
11.【解答】解:由题填写列联表如下,
乐观 不乐观 总计
国内代表 60 40 100
国外代表 40 60 100
总计 100 100 200
,
所以有以上的把握认为持乐观态度和国内外差异有关.
故答案为:有.
12.【解答】解:由样本数据计算得到的观测值,
且,
所以最大有的把握说变量,有关系.
故答案为:.
13.【解答】解:根据分层抽样原理,计算抽取男生(人,
女生(人,
所以(人,
(人,
所以(人.
故答案为:29.
14.【解答】解:由题意得,
解得,
故答案为:15.
四.解答题(共4小题)
15.【解答】解:(1)由题意可知
确诊患新冠肺炎 未确诊患新冠肺炎 合计
50岁及以上 6 34 40
50岁以下 4 56 60
合计 10 90 100
,
所以没有的把握认为是否确诊患新冠肺炎与年龄有关;
(2)现从已确诊的病人中分层抽样抽出5人观察恢复情况,
可知抽取的5人中,有3人是50岁以上的,2人是50岁以下的,
随机抽取3人恰有2人是50岁以上的概率.
16.【解答】解:(Ⅰ)在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是,
,解得,
又,解得.
故,.
(Ⅱ)补充完整的列联表如下所示,
男性 女性 合计
反感 10 8 18
不反感 4 8 12
合计 14 16 30
,
故没有把握认为反感“中国式过马路”与性别有关.
17.【解答】解:(1)由列联表知,,
;
(2)由表中数据,计算的观测值为,
因为,
所以能在犯错误的概率不超过0.005的前提下认为教学方式与成绩有关系.
18.【解答】解:(1)四个理由,任意一个均可,(答案不唯一)
①从以上茎叶图可以看出,药疗效的试验结果有的叶集中在茎2和3上,而药疗效的试验结果有的叶集中在茎0和1上,由此可看出药的疗效更好.
②从茎叶图的分布情况可以看出,服用药的患者日平均增加睡眠时间的平均数大于2,而服用药的患者日平均增加睡眠时间的平均数小于2,因此可知药的疗效更好.
③由茎叶图可知,服用药的患者日平均增加睡眠时间的中位数是,而服用药的患者日平均增加睡眠时间的中位数是,因此药的疗效更好.
④由茎叶图可知,服用药的患者日平均增加睡眠时间分布在茎2上的最多,关于茎2大致呈对称分布;而服用药的患者日平均增加睡眠时间分布在茎1上的最多,关于茎1大致呈对称分布;又患者在服用两种药后日平均增加睡眠时间分布的区间相同,故可以认为服用药的患者日平均增加睡眠时间比服用药的患者日平均增加睡眠时间更多,因此药的疗效更好.
(2)由茎叶图可知,40组数据的中位数为,
因此列联表如下:
超过 不超过
服用药 14 6
服用药 5 15
(3)由于;
所以有的把握认为,两种药的疗效有差异.
