2020-2021学年高中人教A版数学必修3学案 第1章 算法初步 章末综合提升 Word版含解析
文档属性
| 名称 | 2020-2021学年高中人教A版数学必修3学案 第1章 算法初步 章末综合提升 Word版含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 467.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览


文档简介
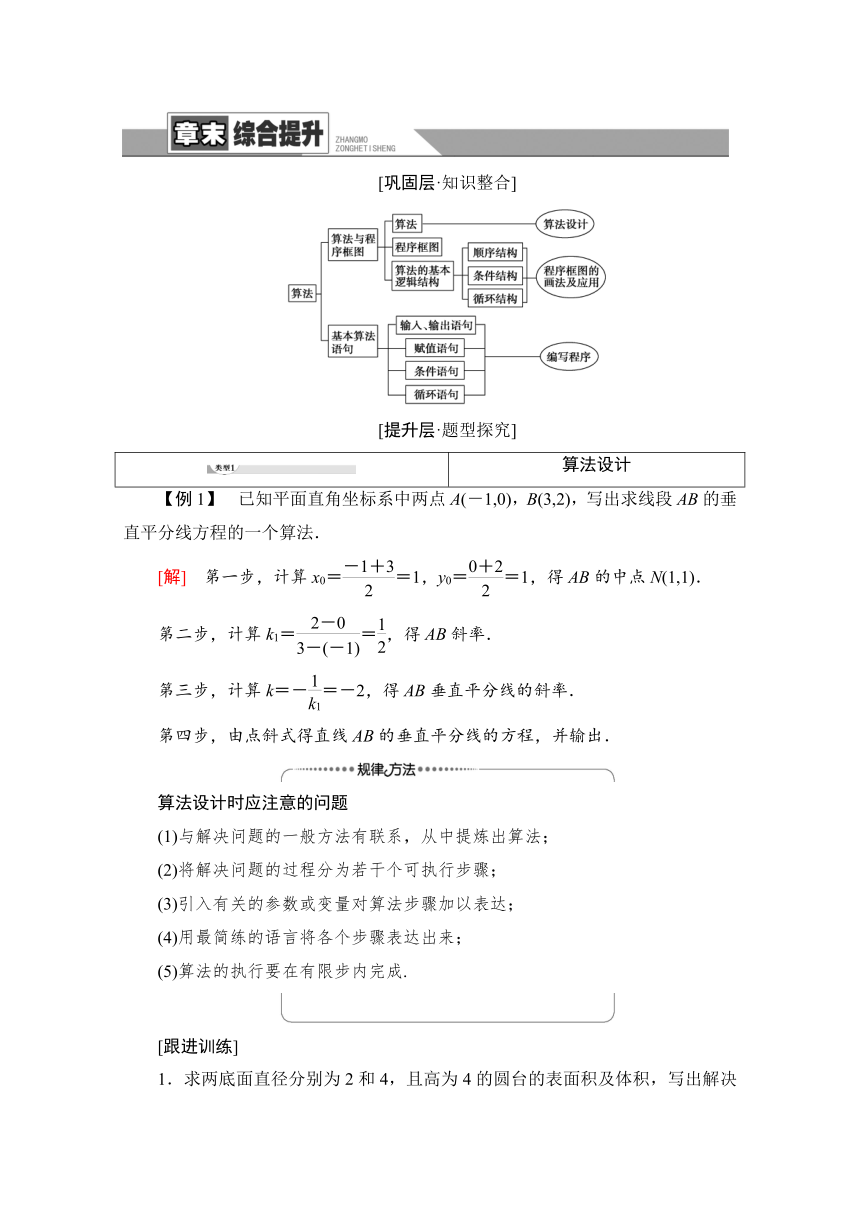
[巩固层·知识整合]
[提升层·题型探究]
算法设计
【例1】 已知平面直角坐标系中两点A(-1,0),B(3,2),写出求线段AB的垂直平分线方程的一个算法.
[解] 第一步,计算x0==1,y0==1,得AB的中点N(1,1).
第二步,计算k1==,得AB斜率.
第三步,计算k=-=-2,得AB垂直平分线的斜率.
第四步,由点斜式得直线AB的垂直平分线的方程,并输出.
算法设计时应注意的问题
(1)与解决问题的一般方法有联系,从中提炼出算法;
(2)将解决问题的过程分为若干个可执行步骤;
(3)引入有关的参数或变量对算法步骤加以表达;
(4)用最简练的语言将各个步骤表达出来;
(5)算法的执行要在有限步内完成.
1.求两底面直径分别为2和4,且高为4的圆台的表面积及体积,写出解决该问题的算法.
[解] 算法如下:
第一步,取r1=1,r2=2,h=4.
第二步,计算l=.
第三步,计算S=πr+πr+π(r1+r2)l与V=π(r+r+r1r2)h.
第四步,输出计算结果.]
画程序框图
【例2】 画出一个计算1×3×5×…×99的程序框图.
[解] 法一:当型循环结构程序框图如图(1)所示.
法二:直到型循环结构程序框图如图(2)所示.
程序框图的画法
对于一个具体的问题,首先设计自然语言描述的算法,这是画框图的基础,其次将算法步骤转化为对应框图.起止框是每个程序框图所不可缺少的,各个框之间用流程线连接,需要断开的地方连接点不可缺少.对于每种框图的功能需要明确,处理框用于数据的处理以及变量的赋值,输入、输出框用于数据的输入与输出,判断框需要填写的是需要进行判断的内容,每个程序框只有一个箭头指向它,并且只能伸出一条流程线(判断框除外).
2.求满足1+2+3+4+…+n>500的最小的正整数n,画出执行该问题的程序框图.
[解] 程序框图:
条件结构与条件语句
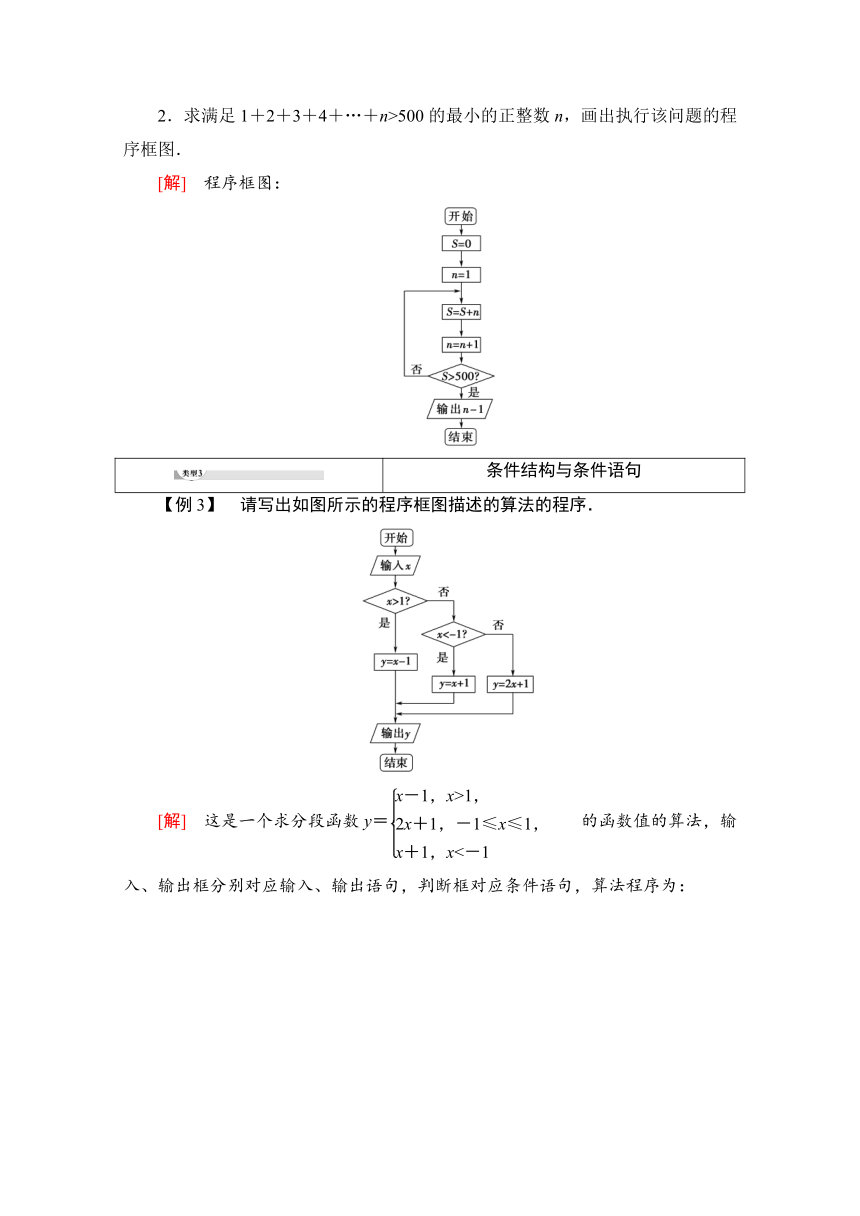
【例3】 请写出如图所示的程序框图描述的算法的程序.
[解] 这是一个求分段函数y=的函数值的算法,输入、输出框分别对应输入、输出语句,判断框对应条件语句,算法程序为:
条件结构与条件语句的应用
(1)条件结构主要用在一些需要依据条件进行判断的算法中,如分段函数的求值,数据的大小比较等.在条件结构中,无论条件是否成立,都只能执行两框之一,两框不可能同时执行,也不可能都不执行.(2)条件语句主要有两种格式,一是IF?THEN?ELSE格式,另一种是IF?THEN格式,它们在用法中有所不同.如果要当表达式的结果为假时,执行另一序列的语句,可采用IF?THEN?ELSE格式,否则,可采用IF?THEN格式.在遇到三段以上分类问题时,往往用到条件语句的嵌套,分清层次,内层执行完再执行外层.
3.请根据下图所示算法语句画出相应的程序框图.算法语句具体如下:
[解] 程序框图如图所示:
循环结构与循环语句
【例4】 计算S=1+(1+2)+(1+2+3)+(1+2+3+4)+…+(1+2+3+4+…+n)的值,画出程序框图并编写程序.
[解] n=1时,S1=1;
n=2时,S2=1+(1+2)=S1+(1+2);
n=3时,S3=S2+(1+2+3);
…
Sn=Sn-1+(1+2+3+4+…+n).
故先考虑Tn=1+2+3+4+…+n的程序框图的画法,求出Tn后,将Sn-1+Tn赋给Sn.
程序框图如下.
程序如下.
循环结构与循环语句的应用
(1)循环结构主要用在一些需要重复执行操作的算法中,如累加、累乘等.循环结构中一定包含条件结构,并且在循环结构中,通常都有一个起循环计数作用的变量,这个变量的取值一般都包括在执行或终止循环的条件中.(2)循环语句也有两种格式,WHILE语句和UNTIL语句.在同一个算法中,它们的判断条件的意义恰好是相反的,初始值有时会不同.当先判断再执行循环体时,用WHILE语句,当先执行循环体再判断时,用UNTIL语句,注意二者间的转化.
4.写出计算-12+22-32+42-…-992+1002的值的程序语句.
[解] 程序语句如下:
[提升层·题型探究]
算法设计
【例1】 已知平面直角坐标系中两点A(-1,0),B(3,2),写出求线段AB的垂直平分线方程的一个算法.
[解] 第一步,计算x0==1,y0==1,得AB的中点N(1,1).
第二步,计算k1==,得AB斜率.
第三步,计算k=-=-2,得AB垂直平分线的斜率.
第四步,由点斜式得直线AB的垂直平分线的方程,并输出.
算法设计时应注意的问题
(1)与解决问题的一般方法有联系,从中提炼出算法;
(2)将解决问题的过程分为若干个可执行步骤;
(3)引入有关的参数或变量对算法步骤加以表达;
(4)用最简练的语言将各个步骤表达出来;
(5)算法的执行要在有限步内完成.
1.求两底面直径分别为2和4,且高为4的圆台的表面积及体积,写出解决该问题的算法.
[解] 算法如下:
第一步,取r1=1,r2=2,h=4.
第二步,计算l=.
第三步,计算S=πr+πr+π(r1+r2)l与V=π(r+r+r1r2)h.
第四步,输出计算结果.]
画程序框图
【例2】 画出一个计算1×3×5×…×99的程序框图.
[解] 法一:当型循环结构程序框图如图(1)所示.
法二:直到型循环结构程序框图如图(2)所示.
程序框图的画法
对于一个具体的问题,首先设计自然语言描述的算法,这是画框图的基础,其次将算法步骤转化为对应框图.起止框是每个程序框图所不可缺少的,各个框之间用流程线连接,需要断开的地方连接点不可缺少.对于每种框图的功能需要明确,处理框用于数据的处理以及变量的赋值,输入、输出框用于数据的输入与输出,判断框需要填写的是需要进行判断的内容,每个程序框只有一个箭头指向它,并且只能伸出一条流程线(判断框除外).
2.求满足1+2+3+4+…+n>500的最小的正整数n,画出执行该问题的程序框图.
[解] 程序框图:
条件结构与条件语句
【例3】 请写出如图所示的程序框图描述的算法的程序.
[解] 这是一个求分段函数y=的函数值的算法,输入、输出框分别对应输入、输出语句,判断框对应条件语句,算法程序为:
条件结构与条件语句的应用
(1)条件结构主要用在一些需要依据条件进行判断的算法中,如分段函数的求值,数据的大小比较等.在条件结构中,无论条件是否成立,都只能执行两框之一,两框不可能同时执行,也不可能都不执行.(2)条件语句主要有两种格式,一是IF?THEN?ELSE格式,另一种是IF?THEN格式,它们在用法中有所不同.如果要当表达式的结果为假时,执行另一序列的语句,可采用IF?THEN?ELSE格式,否则,可采用IF?THEN格式.在遇到三段以上分类问题时,往往用到条件语句的嵌套,分清层次,内层执行完再执行外层.
3.请根据下图所示算法语句画出相应的程序框图.算法语句具体如下:
[解] 程序框图如图所示:
循环结构与循环语句
【例4】 计算S=1+(1+2)+(1+2+3)+(1+2+3+4)+…+(1+2+3+4+…+n)的值,画出程序框图并编写程序.
[解] n=1时,S1=1;
n=2时,S2=1+(1+2)=S1+(1+2);
n=3时,S3=S2+(1+2+3);
…
Sn=Sn-1+(1+2+3+4+…+n).
故先考虑Tn=1+2+3+4+…+n的程序框图的画法,求出Tn后,将Sn-1+Tn赋给Sn.
程序框图如下.
程序如下.
循环结构与循环语句的应用
(1)循环结构主要用在一些需要重复执行操作的算法中,如累加、累乘等.循环结构中一定包含条件结构,并且在循环结构中,通常都有一个起循环计数作用的变量,这个变量的取值一般都包括在执行或终止循环的条件中.(2)循环语句也有两种格式,WHILE语句和UNTIL语句.在同一个算法中,它们的判断条件的意义恰好是相反的,初始值有时会不同.当先判断再执行循环体时,用WHILE语句,当先执行循环体再判断时,用UNTIL语句,注意二者间的转化.
4.写出计算-12+22-32+42-…-992+1002的值的程序语句.
[解] 程序语句如下:
