新人教A版 2020-2021学年 高中第三章 导数及其应用 3.3.1函数的单调性与导案 选修1-1 教案
文档属性
| 名称 | 新人教A版 2020-2021学年 高中第三章 导数及其应用 3.3.1函数的单调性与导案 选修1-1 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 566.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 19:29:01 | ||
图片预览





文档简介
内 容 标 准 学 科 素 养
1.了解导数与函数单调性的关系. 2.掌握利用导数判断函数单调性的方法.
3.能利用导数求不超过三次多项式函数的单调区间. 利用数学抽象
提升逻辑推理
及数学运算
[基础认识]
知识点一 函数的单调性与其导数正负的关系
函数的单调性是怎么定义的?判断单调性的方法有哪些?
提示:如果函数f(x)在定义域内的某区间D上是增函数或减函数,那么就说该函数在区间D上具有单调性.
判断单调性的方法有定义法和图象法.
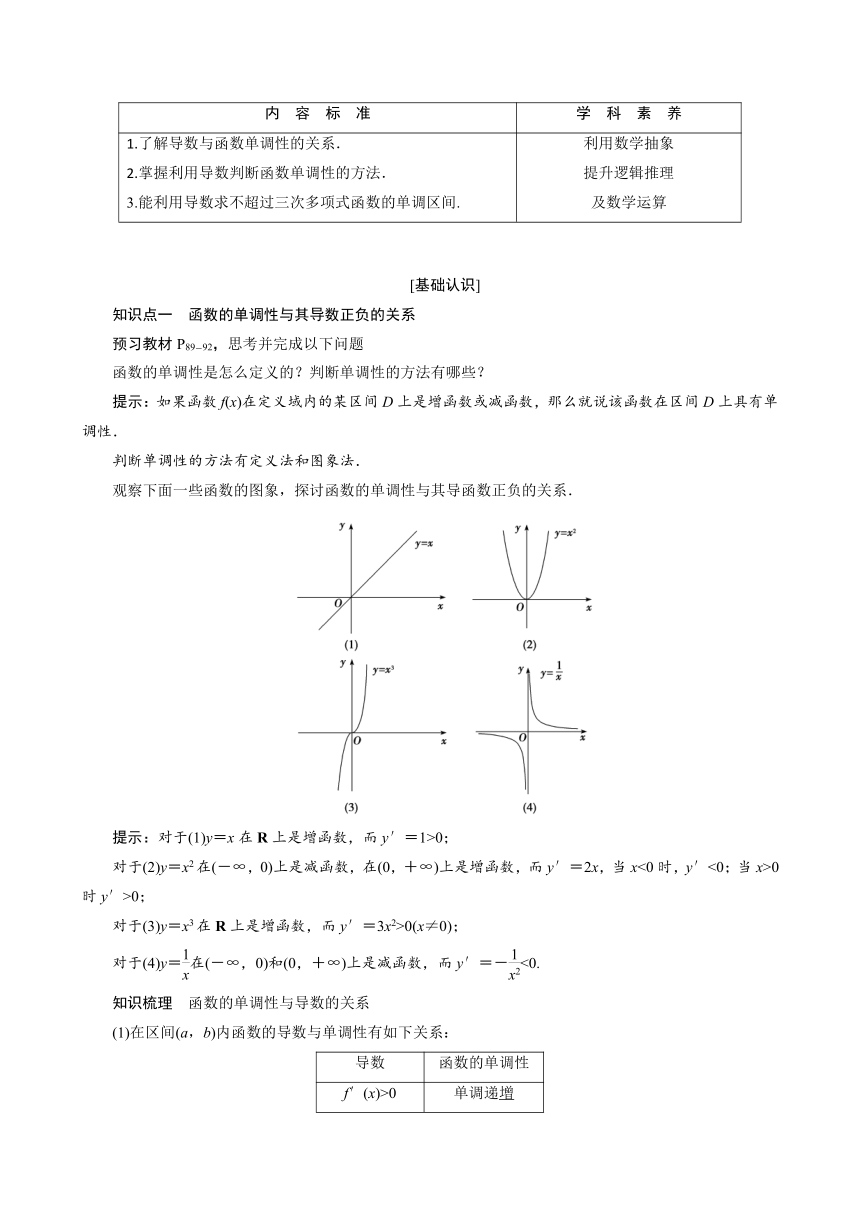
观察下面一些函数的图象,探讨函数的单调性与其导函数正负的关系.
提示:对于(1)y=x在R上是增函数,而y′=1>0;
对于(2)y=x2在(-∞,0)上是减函数,在(0,+∞)上是增函数,而y′=2x,当x<0时,y′<0;当x>0时y′>0;
对于(3)y=x3在R上是增函数,而y′=3x2>0(x≠0);
对于(4)y=在(-∞,0)和(0,+∞)上是减函数,而y′=-<0.
知识梳理 函数的单调性与导数的关系
(1)在区间(a,b)内函数的导数与单调性有如下关系:
导数 函数的单调性
f′(x)>0 单调递增
f′(x)<0 单调递减
f′(x)=0 常函数
(2)在区间(a,b)内函数的单调性与导数有如下关系:
函数的单调性 导数
单调递增 f′(x)≥0
单调递减 f′(x)≤0
常函数 f′(x)=0
特别提醒:(1)若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).
(2)f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为0.
知识点二 函数的变化快慢与导数的关系
通过函数图象,不仅可以看出函数的增或减,还可以看出其变化的快慢.结合图象,你能从导数的角度解释变化快慢的情况吗?
观察下图,函数f(x)在(0,a)和(a,+∞)上都是单调递增的,但在(0,a)内的图象“陡峭”,在(a,+∞)内的图象“平缓”,试比较f(x)在(0,a)和(a,+∞)内导数的大小有什么关系?
提示:根据导数的几何意义,知f(x)在(0,a)内的导数绝对值大于f(x)在(a,+∞)内的导数的绝对值.
知识梳理 函数的变化快慢与导数的关系
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.
[自我检测]
1.函数y=f(x)的导函数f′(x)的图象如图所示,则下列判断中正确的是( )
A.f(x)在(-3,1)上单调递增
B.f(x)在(1,3)上单调递减
C.f(x)在(2,4)上单调递减
D.f(x)在(3,+∞)上单调递增
答案:C
2.函数f(x)=sin x-x在R上是________(填“增函数”或“减函数”).
答案:减函数
探究一 函数与导函数图象间的关系
[阅读教材P91例1]已知导函数f′(x)的下列信息:
当10;
当x>4,或x<1时,f′(x)<0;
当x=4,或x=1时,f′(x)=0.
试画出函数f(x)图象的大致形状.
题型:函数的图象与其导数正负的关系.
方法步骤:①由f′(x)>0得出f(x)在该区间上是增函数.
由f′(x)<0得出f(x)在该区间上是减函数,f(x)=0时为临界点.
②由函数在某区间上的增减性作出f(x)的图象.
[例1] (1)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )
(2)已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
[解析] (1)由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
(2)从f′(x)的图象可以看出,在区间内,导数单调递增;在区间内,导数单调递减.即函数f(x)的图象在内越来越陡,在内越来越平缓,由此可知,只有选项D符合.
[答案] (1)D (2)D
方法技巧 研究函数与导函数图象之间关系的方法
研究一个函数的图象与其导函数图象之间的关系时,注意抓住各自的关键要素,对于原函数,要注意其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,则应注意其函数值在哪个区间内大于零,在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.
跟踪探究 1.函数y=f(x)的图象如图所示,则导函数的图象大致是( )
解析:因为函数f(x)在(0,+∞)和(-∞,0)上都是单调递减的,即f′(x)<0.
答案:D
2.函数y=f(x)在定义域R上有导数,其导函数的图象如图所示,则函数y=f(x)的递增区间为________;递减区间为________.
解析:由f′(x)的图象可知,
当x∈(-2,-1)∪(1,3)∪(4,+∞)时,f′(x)>0;
当x∈(-∞,-2)∪(-1,1)∪(3,4)时,f′(x)<0.
故函数f(x)的增区间为(-2,-1),(1,3),(4,+∞);减区间为(-∞,-2),(-1,1),(3,4).
答案:(-2,-1),(1,3),(4,+∞) (-∞,-2),(-1,1),(3,4)
探究二 利用导数判断(或证明)函数的单调性
[阅读教材P91例2]题型:判断函数的单调性(求单调区间).
方法步骤:①求定义域.
②求导f′(x).
③解不等式f′(x)>0得出f(x)的增区间,解不等式f′(x)<0得出f(x)的减区间.
[例2] (1)求证:函数f(x)=ex-x-1在(0,+∞)内是增函数,在(-∞,0)内是减函数.
[证明] 由于f(x)=ex-x-1,
所以f′(x)=ex-1,
当x∈(0,+∞)时,ex>1,即f′(x)=ex-1>0.
故函数f(x)在(0,+∞)内为增函数,
当x∈(-∞,0)时,ex<1,即f′(x)=ex-1<0.
故函数f(x)在(-∞,0)内为减函数.
(2)求下列函数的单调区间:
①f(x)=x3-2x2+x;
②f(x)=3x2-2ln x.
[解析] ①函数的定义域为R,
∵f(x)=x3-2x2+x,
∴f′(x)=3x2-4x+1.
令f′(x)>0,
解得x>1或x<.
因此f(x)的单调递增区间是,(1,+∞).
令f′(x)<0,解得因此f(x)的单调递减区间是.
②函数的定义域为(0,+∞),
f′(x)=6x-=2·.
令f′(x)>0,即2·>0,
解得-,
又x>0,∴x>;
令f′(x)<0,即2·<0,
解得x<-或0又x>0,∴0∴f(x)的单调递增区间为;
单调递减区间为.
方法技巧 1.利用导数判断函数f(x)在(a,b)内的单调性的步骤
(1)求f′(x);
(2)确定f′(x)在(a,b)内的符号;
(3)得出结论.
2.利用导数求函数单调区间的步骤
(1)求函数的定义域;
(2)求f′(x),解不等式f′(x)>0(或f′(x)<0);
(3)利用不等式的解集与定义域求交集得单调区间.
注意事项:
①求函数的单调区间,必须在函数的定义域内进行.
②如果函数的单调区间有多个时,单调区间不能用“∪”符号连接,只能用“,”或“和”隔开.
③导数法求得的单调区间一般用开区间表示.
跟踪探究 3.函数f(x)=x3-x2-3x+2的单调增区间是________.
解析:x∈R,f′(x)=x2-2x-3=(x-3)(x+1)
由f′(x)>0得x<-1或x>3
∴f(x)的单调增区间是(-∞,-1),(3,+∞)
答案:(-∞,-1),(3,+∞)
4.证明:函数f(x)=在区间上单调递减.
证明:f′(x)=,
又x∈,
则cos x<0,∴xcos x-sin x<0,
∴f′(x)<0,∴f(x)在上单调递减.
探究三 与参数有关的函数单调性问题
[例3] 已知函数f(x)=x3-ax-1.讨论f(x)的单调区间.
[解析] ∵x∈R,∴f′(x)=3x2-a.
(1)当a≤0时,f′(x)≥0,
所以f(x)在(-∞,+∞)上为增函数.
(2)当a>0时,令3x2-a=0,得x=±.
当x>或x<-时,f′(x)>0;
当-因此f(x)在,上为增函数,f(x)在上为减函数.
综上可知,当a≤0时,f(x)在R上为增函数.
当a>0时,f(x)在,上为增函数,在上为减函数.
方法技巧 讨论含有参数的函数的单调性,通常归结为求含参数不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对单调性的影响以及分类讨论的标准.
延伸探究 (1)本例中f(x)不变,若f(x)为单调递增函数,求实数a的取值范围.
解析:(1)由已知得f′(x)=3x2-a,
因为f(x)在(-∞,+∞)上是单调增函数,
所以f′(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立.
因为3x2≥0,
所以只需a≤0.
又因为a=0时,f′(x)=3x2≥0,
f(x)=x3-1在R上是增函数,
所以a≤0.
即实数a的取值范围为(-∞,0].
(2)本例中f(x)不变,若f(x)在区间(1,+∞)内为增函数,求a的取值范围.
解析:(2)因为f′(x)=3x2-a,且f(x)在区间(1,+∞)上为增函数,
所以f′(x)≥0在(1,+∞)恒成立,
即3x2-a≥0在(1,+∞)恒成立,
所以a≤3x2在(1,+∞)恒成立,
即a的取值范围为(-∞,3].
(3)本例中f(x)不变,若f(x)在区间(-1,1)上为减函数,试求a的取值范围.
解析:由f′(x)=3x2-a≤0在(-1,1)上恒成立,得a≥3x2在x∈(-1,1)恒成立.
因为-1所以3x2<3,
所以a≥3.
即a的取值范围是[3,+∞).
(4)本例中f(x)不变,若f(x)的单调递减区间为(-1,1),求a的取值范围.
解析:由例题可知,f(x)的单调递减区间为,∴=1,即a=3.
(5)本例中f(x)不变,若f(x)在区间(-1,1)上不单调,求a的取值范围.
解析:∵f(x)=x3-ax-1,
∴f′(x)=3x2-a,
由f′(x)=0,得x=±(a≥0),
∵f(x)在区间(-1,1)上不单调,
∴0<<1,
即0故a的取值范围为(0,3).
方法技巧 1.已知函数的单调性,求函数解析式中参数的取值范围:
(1)将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
(2)先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
2.恒成立问题的重要思路:
(1)m≥f(x)恒成立?m≥f(x)max;
(2)m≤f(x)恒成立?m≤f(x)min.
跟踪探究 5.(1)若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是________.
(2)试求函数f(x)=kx-ln x的单调区间.
解析:(1)∵f(x)在(1,+∞)上单调递增.
∴f′(x)≥0在(1,+∞)上恒成立.
即k-≥0在(1,+∞)上恒成立
∴k≥在(1,+∞)上恒成立.
∴k≥1.
(2)f(x)=kx-ln x的定义域为(0,+∞),
f′(x)=k-,
当k≤0时,函数的单调递减区间为(0,+∞);
当k>0时,函数的单调递增区间为,单调递减区间为.
答案:(1)[1,+∞) (2)见解析
[课后小结]
(1)导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.
(2)利用导数求函数f(x)的单调区间的一般步骤:
①确定函数f(x)的定义域;
②求导数f′(x);
③在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;
④根据③的结果确定函数f(x)的单调区间.
(3)已知函数的单调性求参数范围,转化为不等式恒成立问题解决.
[素养培优]
1.忽视函数的定义域致错
求函数f(x)=x-ln x的单调区间.
易错分析 由f′(x)>0和f′(x)<0得出不等式的解集即为f(x)的增区间和减区间.忽视函数的定义域致错,考查逻辑推理和数学运算.
自我纠正 x>0,f′(x)=,
由f′(x)>0得x>1,
由f′(x)<0得0∴f(x)的单调增区间为(1,+∞),
单调减区间为(0,1).
2.考虑问题不全面致误
若函数f(x)=x3+x2+mx+1是R上的单调函数,求实数m的取值范围.
易错分析 由f(x)在R上是单调函数得f′(x)>0在R上恒成立,或f′(x)<0在R上恒成立,这种转化不全面,应该f′(x)≥0或f′(x)≤0在R上恒成立,考查逻辑推理的学科素养.
自我纠正 f′(x)=3x2+2x+m.
因为f(x)是R上的单调函数,
所以f′(x)≥0恒成立或f′(x)≤0恒成立.
因为二次项系数3>0,所以只能有f′(x)≥0恒成立.
因此Δ=4-12m≤0,故m≥.
当m=时,使f′(x)=0的点只有一个x=-,也符合题意.
故实数m的取值范围是.
1.了解导数与函数单调性的关系. 2.掌握利用导数判断函数单调性的方法.
3.能利用导数求不超过三次多项式函数的单调区间. 利用数学抽象
提升逻辑推理
及数学运算
[基础认识]
知识点一 函数的单调性与其导数正负的关系
函数的单调性是怎么定义的?判断单调性的方法有哪些?
提示:如果函数f(x)在定义域内的某区间D上是增函数或减函数,那么就说该函数在区间D上具有单调性.
判断单调性的方法有定义法和图象法.
观察下面一些函数的图象,探讨函数的单调性与其导函数正负的关系.
提示:对于(1)y=x在R上是增函数,而y′=1>0;
对于(2)y=x2在(-∞,0)上是减函数,在(0,+∞)上是增函数,而y′=2x,当x<0时,y′<0;当x>0时y′>0;
对于(3)y=x3在R上是增函数,而y′=3x2>0(x≠0);
对于(4)y=在(-∞,0)和(0,+∞)上是减函数,而y′=-<0.
知识梳理 函数的单调性与导数的关系
(1)在区间(a,b)内函数的导数与单调性有如下关系:
导数 函数的单调性
f′(x)>0 单调递增
f′(x)<0 单调递减
f′(x)=0 常函数
(2)在区间(a,b)内函数的单调性与导数有如下关系:
函数的单调性 导数
单调递增 f′(x)≥0
单调递减 f′(x)≤0
常函数 f′(x)=0
特别提醒:(1)若在某区间上有有限个点使f′(x)=0,在其余的点恒有f′(x)>0,则f(x)仍为增函数(减函数的情形完全类似).
(2)f(x)为增函数的充要条件是对任意的x∈(a,b)都有f′(x)≥0且在(a,b)内的任一非空子区间上f′(x)不恒为0.
知识点二 函数的变化快慢与导数的关系
通过函数图象,不仅可以看出函数的增或减,还可以看出其变化的快慢.结合图象,你能从导数的角度解释变化快慢的情况吗?
观察下图,函数f(x)在(0,a)和(a,+∞)上都是单调递增的,但在(0,a)内的图象“陡峭”,在(a,+∞)内的图象“平缓”,试比较f(x)在(0,a)和(a,+∞)内导数的大小有什么关系?
提示:根据导数的几何意义,知f(x)在(0,a)内的导数绝对值大于f(x)在(a,+∞)内的导数的绝对值.
知识梳理 函数的变化快慢与导数的关系
一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得快,这时,函数的图象就比较“陡峭”(向上或向下);反之,函数的图象就“平缓”一些.
[自我检测]
1.函数y=f(x)的导函数f′(x)的图象如图所示,则下列判断中正确的是( )
A.f(x)在(-3,1)上单调递增
B.f(x)在(1,3)上单调递减
C.f(x)在(2,4)上单调递减
D.f(x)在(3,+∞)上单调递增
答案:C
2.函数f(x)=sin x-x在R上是________(填“增函数”或“减函数”).
答案:减函数
探究一 函数与导函数图象间的关系
[阅读教材P91例1]已知导函数f′(x)的下列信息:
当1
当x>4,或x<1时,f′(x)<0;
当x=4,或x=1时,f′(x)=0.
试画出函数f(x)图象的大致形状.
题型:函数的图象与其导数正负的关系.
方法步骤:①由f′(x)>0得出f(x)在该区间上是增函数.
由f′(x)<0得出f(x)在该区间上是减函数,f(x)=0时为临界点.
②由函数在某区间上的增减性作出f(x)的图象.
[例1] (1)设函数f(x)在定义域内可导,y=f(x)的图象如图所示,则导函数y=f′(x)的图象可能为( )
(2)已知f′(x)是f(x)的导函数,f′(x)的图象如图所示,则f(x)的图象只可能是( )
[解析] (1)由函数的图象可知:当x<0时,函数单调递增,导数始终为正;当x>0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.
(2)从f′(x)的图象可以看出,在区间内,导数单调递增;在区间内,导数单调递减.即函数f(x)的图象在内越来越陡,在内越来越平缓,由此可知,只有选项D符合.
[答案] (1)D (2)D
方法技巧 研究函数与导函数图象之间关系的方法
研究一个函数的图象与其导函数图象之间的关系时,注意抓住各自的关键要素,对于原函数,要注意其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,则应注意其函数值在哪个区间内大于零,在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.
跟踪探究 1.函数y=f(x)的图象如图所示,则导函数的图象大致是( )
解析:因为函数f(x)在(0,+∞)和(-∞,0)上都是单调递减的,即f′(x)<0.
答案:D
2.函数y=f(x)在定义域R上有导数,其导函数的图象如图所示,则函数y=f(x)的递增区间为________;递减区间为________.
解析:由f′(x)的图象可知,
当x∈(-2,-1)∪(1,3)∪(4,+∞)时,f′(x)>0;
当x∈(-∞,-2)∪(-1,1)∪(3,4)时,f′(x)<0.
故函数f(x)的增区间为(-2,-1),(1,3),(4,+∞);减区间为(-∞,-2),(-1,1),(3,4).
答案:(-2,-1),(1,3),(4,+∞) (-∞,-2),(-1,1),(3,4)
探究二 利用导数判断(或证明)函数的单调性
[阅读教材P91例2]题型:判断函数的单调性(求单调区间).
方法步骤:①求定义域.
②求导f′(x).
③解不等式f′(x)>0得出f(x)的增区间,解不等式f′(x)<0得出f(x)的减区间.
[例2] (1)求证:函数f(x)=ex-x-1在(0,+∞)内是增函数,在(-∞,0)内是减函数.
[证明] 由于f(x)=ex-x-1,
所以f′(x)=ex-1,
当x∈(0,+∞)时,ex>1,即f′(x)=ex-1>0.
故函数f(x)在(0,+∞)内为增函数,
当x∈(-∞,0)时,ex<1,即f′(x)=ex-1<0.
故函数f(x)在(-∞,0)内为减函数.
(2)求下列函数的单调区间:
①f(x)=x3-2x2+x;
②f(x)=3x2-2ln x.
[解析] ①函数的定义域为R,
∵f(x)=x3-2x2+x,
∴f′(x)=3x2-4x+1.
令f′(x)>0,
解得x>1或x<.
因此f(x)的单调递增区间是,(1,+∞).
令f′(x)<0,解得
②函数的定义域为(0,+∞),
f′(x)=6x-=2·.
令f′(x)>0,即2·>0,
解得-
又x>0,∴x>;
令f′(x)<0,即2·<0,
解得x<-或0
单调递减区间为.
方法技巧 1.利用导数判断函数f(x)在(a,b)内的单调性的步骤
(1)求f′(x);
(2)确定f′(x)在(a,b)内的符号;
(3)得出结论.
2.利用导数求函数单调区间的步骤
(1)求函数的定义域;
(2)求f′(x),解不等式f′(x)>0(或f′(x)<0);
(3)利用不等式的解集与定义域求交集得单调区间.
注意事项:
①求函数的单调区间,必须在函数的定义域内进行.
②如果函数的单调区间有多个时,单调区间不能用“∪”符号连接,只能用“,”或“和”隔开.
③导数法求得的单调区间一般用开区间表示.
跟踪探究 3.函数f(x)=x3-x2-3x+2的单调增区间是________.
解析:x∈R,f′(x)=x2-2x-3=(x-3)(x+1)
由f′(x)>0得x<-1或x>3
∴f(x)的单调增区间是(-∞,-1),(3,+∞)
答案:(-∞,-1),(3,+∞)
4.证明:函数f(x)=在区间上单调递减.
证明:f′(x)=,
又x∈,
则cos x<0,∴xcos x-sin x<0,
∴f′(x)<0,∴f(x)在上单调递减.
探究三 与参数有关的函数单调性问题
[例3] 已知函数f(x)=x3-ax-1.讨论f(x)的单调区间.
[解析] ∵x∈R,∴f′(x)=3x2-a.
(1)当a≤0时,f′(x)≥0,
所以f(x)在(-∞,+∞)上为增函数.
(2)当a>0时,令3x2-a=0,得x=±.
当x>或x<-时,f′(x)>0;
当-
综上可知,当a≤0时,f(x)在R上为增函数.
当a>0时,f(x)在,上为增函数,在上为减函数.
方法技巧 讨论含有参数的函数的单调性,通常归结为求含参数不等式的解集问题,而对含有参数的不等式要针对具体情况进行讨论,但要始终注意定义域对单调性的影响以及分类讨论的标准.
延伸探究 (1)本例中f(x)不变,若f(x)为单调递增函数,求实数a的取值范围.
解析:(1)由已知得f′(x)=3x2-a,
因为f(x)在(-∞,+∞)上是单调增函数,
所以f′(x)=3x2-a≥0在(-∞,+∞)上恒成立,
即a≤3x2对x∈R恒成立.
因为3x2≥0,
所以只需a≤0.
又因为a=0时,f′(x)=3x2≥0,
f(x)=x3-1在R上是增函数,
所以a≤0.
即实数a的取值范围为(-∞,0].
(2)本例中f(x)不变,若f(x)在区间(1,+∞)内为增函数,求a的取值范围.
解析:(2)因为f′(x)=3x2-a,且f(x)在区间(1,+∞)上为增函数,
所以f′(x)≥0在(1,+∞)恒成立,
即3x2-a≥0在(1,+∞)恒成立,
所以a≤3x2在(1,+∞)恒成立,
即a的取值范围为(-∞,3].
(3)本例中f(x)不变,若f(x)在区间(-1,1)上为减函数,试求a的取值范围.
解析:由f′(x)=3x2-a≤0在(-1,1)上恒成立,得a≥3x2在x∈(-1,1)恒成立.
因为-1
所以a≥3.
即a的取值范围是[3,+∞).
(4)本例中f(x)不变,若f(x)的单调递减区间为(-1,1),求a的取值范围.
解析:由例题可知,f(x)的单调递减区间为,∴=1,即a=3.
(5)本例中f(x)不变,若f(x)在区间(-1,1)上不单调,求a的取值范围.
解析:∵f(x)=x3-ax-1,
∴f′(x)=3x2-a,
由f′(x)=0,得x=±(a≥0),
∵f(x)在区间(-1,1)上不单调,
∴0<<1,
即0
方法技巧 1.已知函数的单调性,求函数解析式中参数的取值范围:
(1)将问题转化为不等式在某区间上的恒成立问题,即f′(x)≥0(或f′(x)≤0)恒成立,利用分离参数或函数性质求解参数范围,然后检验参数取“=”时是否满足题意.
(2)先令f′(x)>0(或f′(x)<0),求出参数的取值范围后,再验证参数取“=”时f(x)是否满足题意.
2.恒成立问题的重要思路:
(1)m≥f(x)恒成立?m≥f(x)max;
(2)m≤f(x)恒成立?m≤f(x)min.
跟踪探究 5.(1)若函数f(x)=kx-ln x在区间(1,+∞)上单调递增,则k的取值范围是________.
(2)试求函数f(x)=kx-ln x的单调区间.
解析:(1)∵f(x)在(1,+∞)上单调递增.
∴f′(x)≥0在(1,+∞)上恒成立.
即k-≥0在(1,+∞)上恒成立
∴k≥在(1,+∞)上恒成立.
∴k≥1.
(2)f(x)=kx-ln x的定义域为(0,+∞),
f′(x)=k-,
当k≤0时,函数的单调递减区间为(0,+∞);
当k>0时,函数的单调递增区间为,单调递减区间为.
答案:(1)[1,+∞) (2)见解析
[课后小结]
(1)导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.
(2)利用导数求函数f(x)的单调区间的一般步骤:
①确定函数f(x)的定义域;
②求导数f′(x);
③在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0;
④根据③的结果确定函数f(x)的单调区间.
(3)已知函数的单调性求参数范围,转化为不等式恒成立问题解决.
[素养培优]
1.忽视函数的定义域致错
求函数f(x)=x-ln x的单调区间.
易错分析 由f′(x)>0和f′(x)<0得出不等式的解集即为f(x)的增区间和减区间.忽视函数的定义域致错,考查逻辑推理和数学运算.
自我纠正 x>0,f′(x)=,
由f′(x)>0得x>1,
由f′(x)<0得0
单调减区间为(0,1).
2.考虑问题不全面致误
若函数f(x)=x3+x2+mx+1是R上的单调函数,求实数m的取值范围.
易错分析 由f(x)在R上是单调函数得f′(x)>0在R上恒成立,或f′(x)<0在R上恒成立,这种转化不全面,应该f′(x)≥0或f′(x)≤0在R上恒成立,考查逻辑推理的学科素养.
自我纠正 f′(x)=3x2+2x+m.
因为f(x)是R上的单调函数,
所以f′(x)≥0恒成立或f′(x)≤0恒成立.
因为二次项系数3>0,所以只能有f′(x)≥0恒成立.
因此Δ=4-12m≤0,故m≥.
当m=时,使f′(x)=0的点只有一个x=-,也符合题意.
故实数m的取值范围是.
