人教数六年级数学下册-整理和复习——比和比例 课件(42张PPT)
文档属性
| 名称 | 人教数六年级数学下册-整理和复习——比和比例 课件(42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 06:30:25 | ||
图片预览







文档简介
(共41张PPT)
整理与复习 比和比例
小学六年级 数学
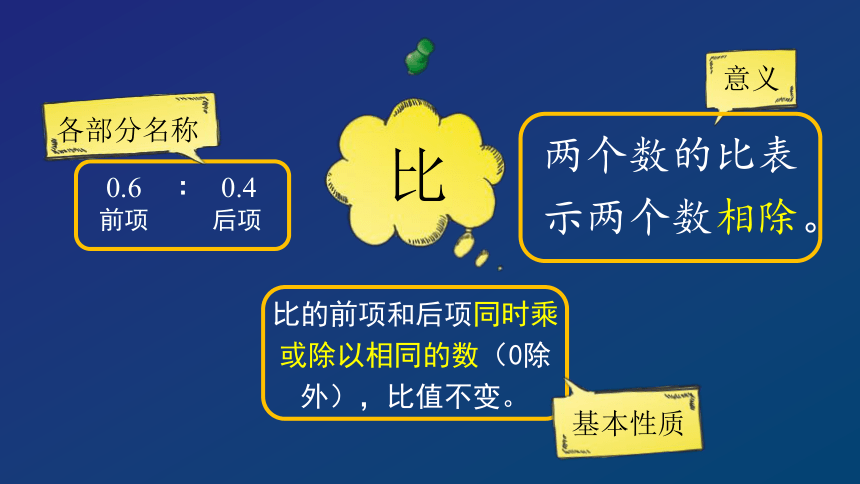
0.6 ∶ 0.4
前项 后项
比
意义
各部分名称
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
基本性质
两个数的比表示两个数相除。
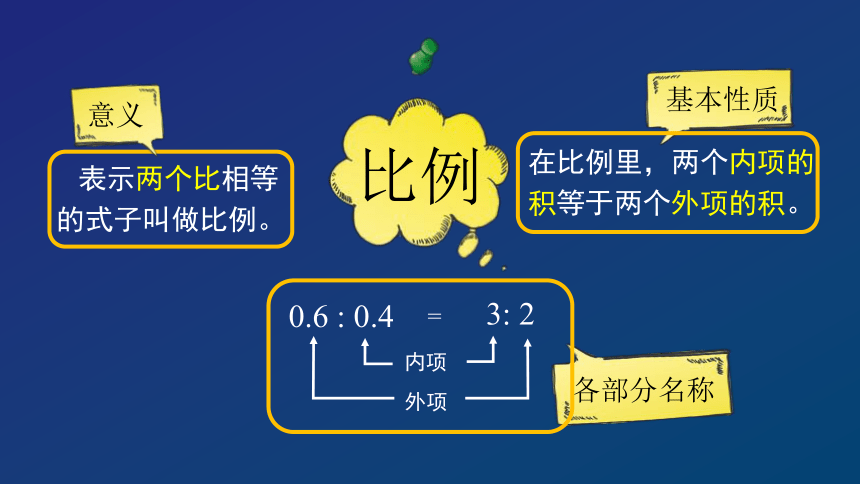
表示两个比相等的式子叫做比例。
比例
基本性质
意义
在比例里,两个内项的积等于两个外项的积。
各部分名称
外项
内项
3: 2
0.6 : 0.4
=
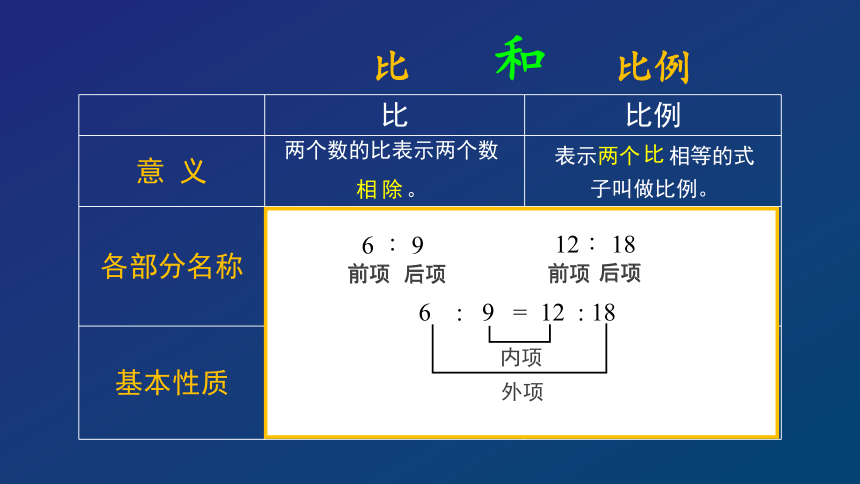
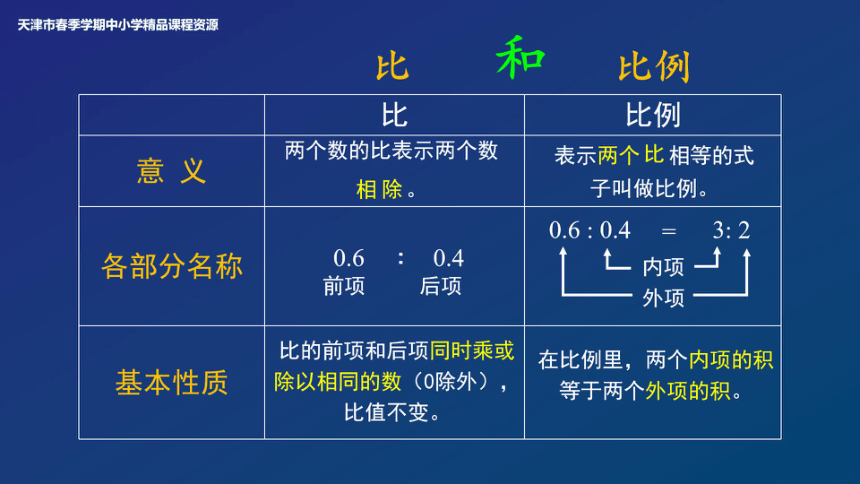
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
①1.5 : 2.4
=1.5÷2.4=
② 5 : 8
= 5÷8 =
1.5 : 2.4
5 : 8
=
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
6 ∶9
12 ∶18
前项
后项
前项
后项
6 : 9 = 12 : 18
内项
外项
前项
后项
前项
后项
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
5 : 8
5×8×3
8×5×3
= 8×5×3
×3
×3
15
: 24
=
( 1 )六年级男生有 80 人,女生有 84 人,男生与女生人数之比为 _ 。
( 2 )小明身高160cm,他一庹长也是160cm,二者之比为 。
( 3 )小丽的脚长23cm ,她的身高是 161 cm ,她的脚长与身高之比为 _ 。
( 4 )如果 3a = 5b ( a、b≠0) ,那么 a : b = _ 。
1 : 1
80 : 84
20 : 21
5 : 3
160:160
1 :7
23 : 161
(教材第85页第1题)
tuǒ
比与分数、除法的关系
联系 例子
区别
各部分名称 分数 分 子 分数线 分 母 分数值 分数是一种数
除法 被除数 除 号 除 数 商 5÷8 除法是一种运算
比 前 项 比 号 后 项 比 值 5:8 比是两个数之间的
倍数关系
a
b
= a ÷ b = a :b (b ≠ 0)
5
8
a
b
= a ÷ b = a :b (b ≠ 0)
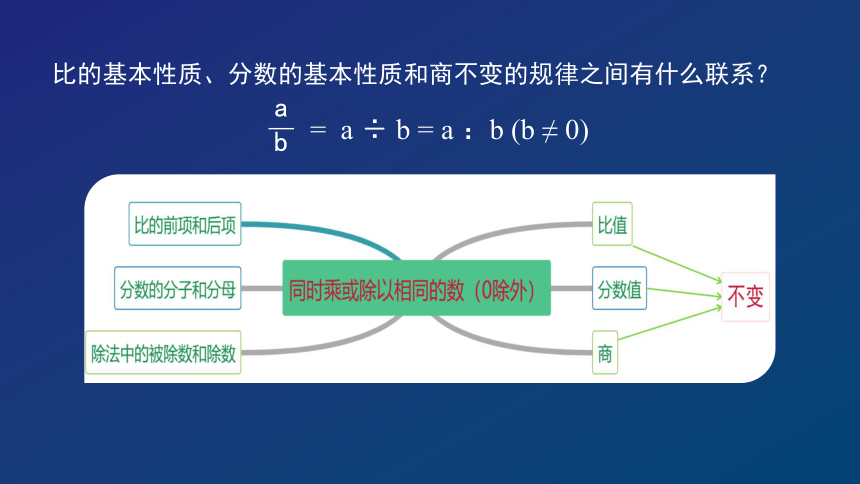
比的基本性质、分数的基本性质和商不变的规律之间有什么联系?
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
1 + 8 = 9
氢:5.4÷9×1=0.6(kg)
氧:5.4÷9×8=4.8(kg)
答:5.4kg的水中含氢0.6kg,氧4.8kg。
1
9
8
9
1 + 8 = 9
氢:5.4× = 0.6 (kg)
氧:5.4× = 4.8 (kg)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
解:设北京到济南全程需要x小时。
120x = 430×1.5 x = 5.375
答:北京到济南全程需要5.375小时。
430
x
120
1.5
=
速度不变,即路程与时间的比值一定
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
路程
时间
=速度(一定)
总页数不变,即每天读的页数与天数的乘积一定
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天读页数×天数 = 总页数(一定)
解:设平均每天要读x页。
6x=30×8
6x=240
x =40
答:平均每天要读40页。
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
路程
时间
40
0.5
80
1
120
1.5
160
2
200
2.5
240
3
...
...
0
40
0.5
2
3
4
时间/时
路程/km
1
1.5
2.5
3.5
80
120
160
200
240
280
320
(1.5,120)
(1,80)
(2,160)
(2.5,200)
(3,240)
(k一定)
(0.5,40)
×2
×2
÷3
÷3
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天页数
天数
60
4
48
5
40
6
7
30
8
...
...
(教材第64页第8题)
×2
÷2
(k一定)
240
7
0
30
1
8
天数/天
每天页数/页
2
4
60
90
120
150
180
(6,40)
(5,48)
(8,30)
(4,60)
3
5
6
7
210
240
(1,240)
(2,120)
(3,80)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
出勤人数+缺勤人数=全班人数(一定)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
比值一定
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
三角形的面积×2=底×高 积一定
(成反比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
表面积
一个面面积
= 6 比值一定
(成正比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
(成正比例)
乘积一定
(成反比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
(成正比例)
(成反比例)
(成正比例)
花生油的质量
花生的质量
×100%= 出油率 商一定
在同一幅地图上,量得甲乙两地的直线距离是 20 cm ,甲丙两地的直线距离是 12 cm ,如果甲乙两地的实际距离是 1600 km ,那么甲丙两地的实际距离是多少?
(教材第85页第6题)
=
1
8000000
12÷ =96000000cm
96000000cm=960km
1
8000000
1600km=160000000cm
答:甲丙两地的实际距离是960km。
20
160000000
图上距离
实际距离
=比例尺
行驶路程 / km
离校距离 / km
(教材第85页第7题)
反思与回顾
同学们 再见!
加工一批零件,原计划要18小时完成,改进工艺后只需12小时就能完成,实际每小时比原计划每小时多加工8个零件,这批零件共有多少个?
解:设原计划每小时加工x个零件。
18 x =12×(x+8)
(18-12)x =12×8
x =16
18×16=288(个)
答:这批零件共有288个。
工作总量不变,即工作效率与工作时间的乘积一定。
工程问题
伦敦奥运会一块金牌的黄金含量与金牌总币的比为 6 : 412 。一块金牌总412g , 302块金牌需要黄金多少克?
421÷412×6 = 6 (g)
6 × 302 = 1812(g)
答:302块金牌需要黄金1812克。
(教材第85页第4题)
整理与复习 比和比例
小学六年级 数学
0.6 ∶ 0.4
前项 后项
比
意义
各部分名称
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
基本性质
两个数的比表示两个数相除。
表示两个比相等的式子叫做比例。
比例
基本性质
意义
在比例里,两个内项的积等于两个外项的积。
各部分名称
外项
内项
3: 2
0.6 : 0.4
=
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
①1.5 : 2.4
=1.5÷2.4=
② 5 : 8
= 5÷8 =
1.5 : 2.4
5 : 8
=
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
6 ∶9
12 ∶18
前项
后项
前项
后项
6 : 9 = 12 : 18
内项
外项
前项
后项
前项
后项
和
比 比例
意 义
各部分名称
基本性质
两个数的比表示两个数相 。
表示两个 相等的式子叫做比例。
0.6 ∶ 0.4
前项 后项
外项
内项
3: 2
0.6 : 0.4
=
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
比
比例
除
比
5 : 8
5×8×3
8×5×3
= 8×5×3
×3
×3
15
: 24
=
( 1 )六年级男生有 80 人,女生有 84 人,男生与女生人数之比为 _ 。
( 2 )小明身高160cm,他一庹长也是160cm,二者之比为 。
( 3 )小丽的脚长23cm ,她的身高是 161 cm ,她的脚长与身高之比为 _ 。
( 4 )如果 3a = 5b ( a、b≠0) ,那么 a : b = _ 。
1 : 1
80 : 84
20 : 21
5 : 3
160:160
1 :7
23 : 161
(教材第85页第1题)
tuǒ
比与分数、除法的关系
联系 例子
区别
各部分名称 分数 分 子 分数线 分 母 分数值 分数是一种数
除法 被除数 除 号 除 数 商 5÷8 除法是一种运算
比 前 项 比 号 后 项 比 值 5:8 比是两个数之间的
倍数关系
a
b
= a ÷ b = a :b (b ≠ 0)
5
8
a
b
= a ÷ b = a :b (b ≠ 0)
比的基本性质、分数的基本性质和商不变的规律之间有什么联系?
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
1 + 8 = 9
氢:5.4÷9×1=0.6(kg)
氧:5.4÷9×8=4.8(kg)
答:5.4kg的水中含氢0.6kg,氧4.8kg。
1
9
8
9
1 + 8 = 9
氢:5.4× = 0.6 (kg)
氧:5.4× = 4.8 (kg)
水是由氢和氧按1 : 8 的质量比化合而成的。5.4 kg 的水含氢和氧各多少?
(教材第85页第3题)
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
解:设北京到济南全程需要x小时。
120x = 430×1.5 x = 5.375
答:北京到济南全程需要5.375小时。
430
x
120
1.5
=
速度不变,即路程与时间的比值一定
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
路程
时间
=速度(一定)
总页数不变,即每天读的页数与天数的乘积一定
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天读页数×天数 = 总页数(一定)
解:设平均每天要读x页。
6x=30×8
6x=240
x =40
答:平均每天要读40页。
北京到济南高速公路距离大约为 430km ,北京到天津大约为 120 km,一辆汽车从北京出发开往济南,当行驶到天津时用了 1.5小时。按照这个速度 ,北京到济南全程需要多少小时?
(教材第85页第5题)
路程
时间
40
0.5
80
1
120
1.5
160
2
200
2.5
240
3
...
...
0
40
0.5
2
3
4
时间/时
路程/km
1
1.5
2.5
3.5
80
120
160
200
240
280
320
(1.5,120)
(1,80)
(2,160)
(2.5,200)
(3,240)
(k一定)
(0.5,40)
×2
×2
÷3
÷3
(教材第64页第8题)
小林读一本文学名著,如果每天读30页,8天可以读完,小林想6天读完,那么平均每天要读多少页?
每天页数
天数
60
4
48
5
40
6
7
30
8
...
...
(教材第64页第8题)
×2
÷2
(k一定)
240
7
0
30
1
8
天数/天
每天页数/页
2
4
60
90
120
150
180
(6,40)
(5,48)
(8,30)
(4,60)
3
5
6
7
210
240
(1,240)
(2,120)
(3,80)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
出勤人数+缺勤人数=全班人数(一定)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
比值一定
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
三角形的面积×2=底×高 积一定
(成反比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
表面积
一个面面积
= 6 比值一定
(成正比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
(成正比例)
乘积一定
(成反比例)
判断下面各题中的两个量是否成正比例或反比例关系。
y
x
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 = 3 ,y 与 x 。
(3)三角形的面积一定,它的底与高。
(教材第85页第2题)
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1 , y 与 x 。
(6)出油率一定,花生油的质量与花生的质量。
(不成比例)
(成正比例)
(成反比例)
(成正比例)
(成反比例)
(成正比例)
花生油的质量
花生的质量
×100%= 出油率 商一定
在同一幅地图上,量得甲乙两地的直线距离是 20 cm ,甲丙两地的直线距离是 12 cm ,如果甲乙两地的实际距离是 1600 km ,那么甲丙两地的实际距离是多少?
(教材第85页第6题)
=
1
8000000
12÷ =96000000cm
96000000cm=960km
1
8000000
1600km=160000000cm
答:甲丙两地的实际距离是960km。
20
160000000
图上距离
实际距离
=比例尺
行驶路程 / km
离校距离 / km
(教材第85页第7题)
反思与回顾
同学们 再见!
加工一批零件,原计划要18小时完成,改进工艺后只需12小时就能完成,实际每小时比原计划每小时多加工8个零件,这批零件共有多少个?
解:设原计划每小时加工x个零件。
18 x =12×(x+8)
(18-12)x =12×8
x =16
18×16=288(个)
答:这批零件共有288个。
工作总量不变,即工作效率与工作时间的乘积一定。
工程问题
伦敦奥运会一块金牌的黄金含量与金牌总币的比为 6 : 412 。一块金牌总412g , 302块金牌需要黄金多少克?
421÷412×6 = 6 (g)
6 × 302 = 1812(g)
答:302块金牌需要黄金1812克。
(教材第85页第4题)
