人教数六年级数学下册-《整理和复习——图形的测量》 课件(59张ppt)
文档属性
| 名称 | 人教数六年级数学下册-《整理和复习——图形的测量》 课件(59张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 57.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 06:35:21 | ||
图片预览






文档简介
(共59张PPT)
整理和复习——图形的测量
小学六年级 数学
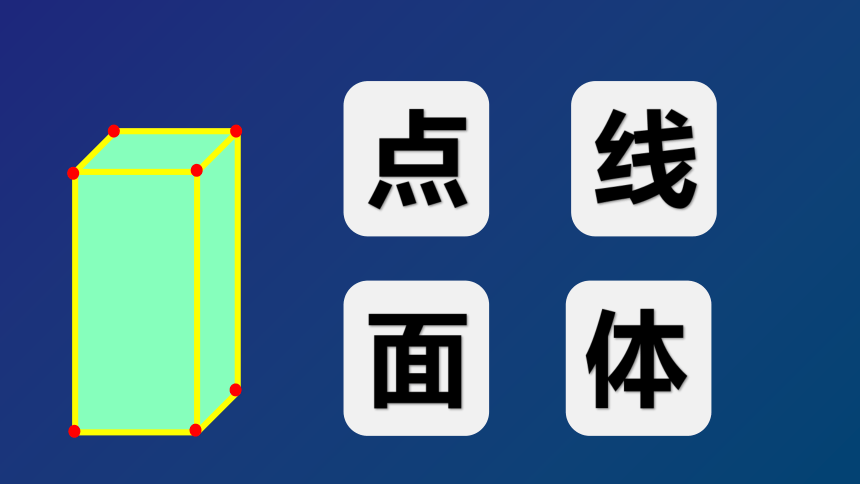
点
线
面
体
线
面
体
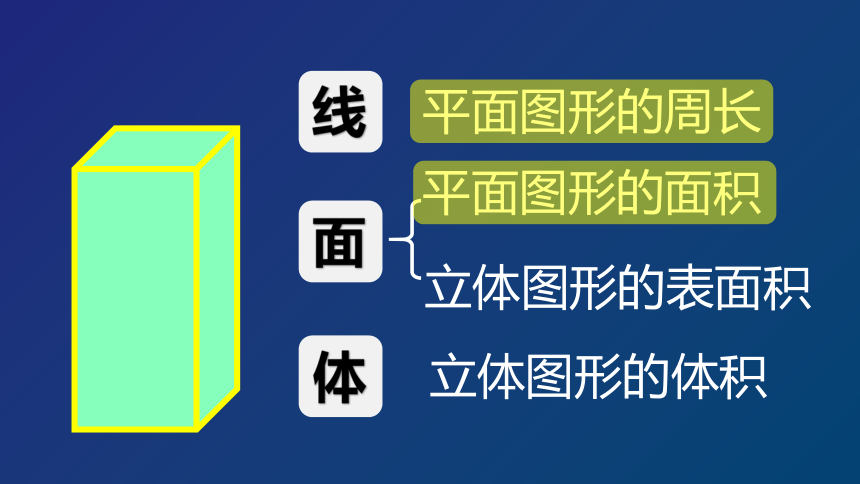
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
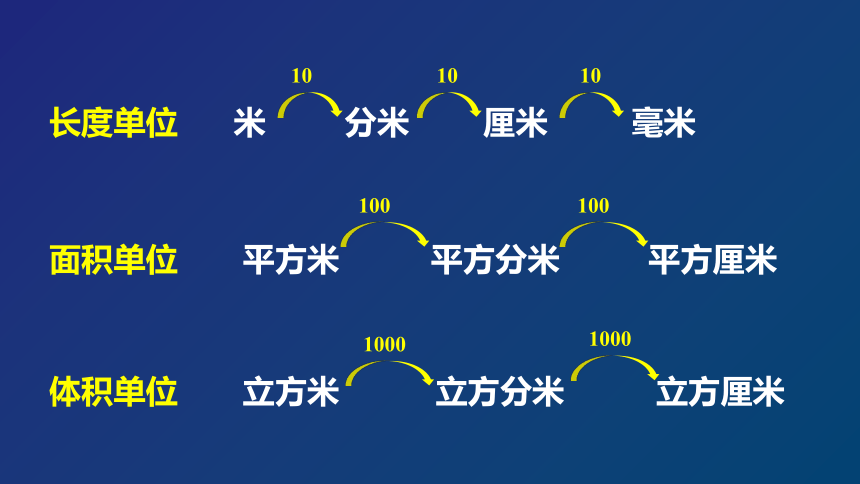
长度单位
米
分米
厘米
毫米
面积单位
平方米
平方分米
平方厘米
体积单位
立方米
立方分米
立方厘米
10
10
10
100
100
1000
1000
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
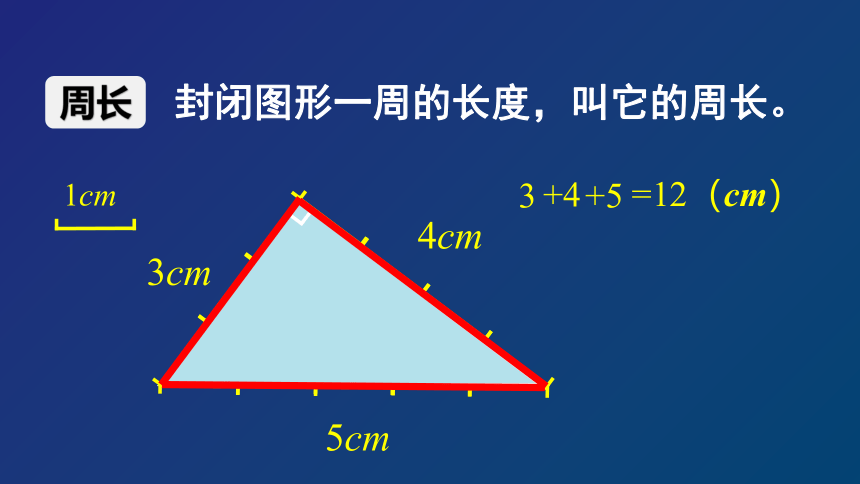
周长
封闭图形一周的长度,叫它的周长。
3
1cm
4cm
3cm
5cm
3
+4
+5
=12(cm)
3
两组对边分别相等
C=(a+b )×2
四条边都相等
C=4a
周长和直径的比值是圆周率
C=πd
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
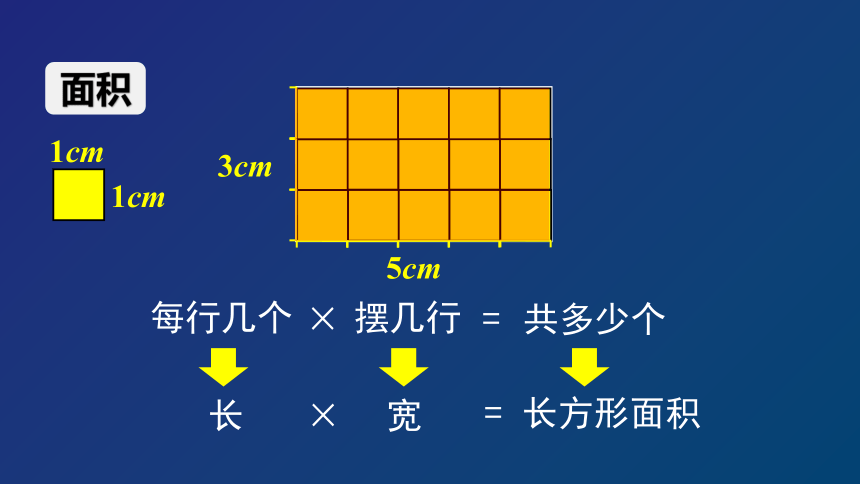
面积
面积
1cm
1cm
5cm
3cm
每行几个
摆几行
共多少个
×
=
长
宽
×
=
长方形面积
长方形面积= 长 × 宽
正方形面积=
边长
边长
S=a
×
a
b
a
S=ab
S=a
先沿高剪开,把三角形向又平移再剪成
可以把平行四边形变成一个长方形
转换成长方形就能计算面积了
平行四边形面积=底×高
S=ah
a
b
a
a
┐
h
S=ab
S=a
S=ah
三角形面积=底×高÷2
S=ah÷2
S=(a+b)÷2
a
b
a
a
┐
h
┐
┐
a
a
b
h
h
S=ab
S=a
S=ah
S=ah÷2
梯形面积公式=(上底+下底)×高÷2
S=(a+b)×h÷2
分割
增补
割补
S=πr
圆的面积=周长的一半×半径
r
a
b
a
a
┐
h
┐
┐
a
a
b
h
h
S=ab
S=a
S=ah
S=ah÷2
S=(a+b)÷2
r
S=πr
需要探索的新图形
转化
学习过的旧图形
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
教材第89页 第4题
每一组中两个图形的周长相等么?面积呢?
周长不相等,面积相等
周长相等,面积不相等
教材第89页 第4题
每一组中两个图形的周长相等么?面积呢?
图形的周长和它的面积大小无关。
教材第90页 第6题
一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
平行四边形面积=底×高
三角形面积=底×高÷2
30÷2=15(cm )
底
高
答:三角形的面积是15cm 。
教材第90页 第6题
一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
平行四边形面积=底×高
三角形面积=底×高÷2
15×2=30(cm )
底
高
答:平行四边形的面积是30cm 。
三角形
的面积是15cm ,平行四边形的面积是多少?
底
高
等底等高的平行四边形和三角形,平行四边形的面积是三角形面积的两倍,三角形的面积是平行四边形面积的二分之一。
等底
等高
三角形面积:15cm
平行四边形面积:30cm
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
6个面的总面积
3个面的总面积
表面积
图形 面的特点
6个面,相对的面是面积相等的长方形
6个相同的面,每个面都是正方形
长方体表面积=上、下面面积+左、右面面积+前、后面的面积
正方体表面积=每个面的面积×6
S=2ab+2bh+2ah
S=6a
圆柱的表面积=圆柱的侧面面积+两个底面的面积
底面周长×高
S表=Ch+2S底
体积
物体所占空间的大小叫做物体的体积。
8cm
5cm
4cm
1cm
8×4×5=160(cm )
长
宽
高
体积
物体所占空间的大小叫做物体的体积。
长方体所含体积单位的数量就是长方体的体积
长方体的体积正好等于长×宽×高的积
长方体体积=长×宽×高
V=abh
长方体体积=长 × 宽 × 高
=棱长×棱长×棱长
正方体体积
V=a
V=πr h
圆柱体积=底面积×高
S
S
S
h
h
h
V=Sh
圆锥体积等于与它等底等高圆柱体积的三分之一。
V= πr h
1
3
把一个棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高大约是多少?(得数保留整厘米。)
正方体体积=圆锥体积
熔铸
正方体体积:10×10×10=1000(cm )
(圆锥体积)
圆锥的半径:20÷2=10(cm)
圆锥的底面积:10×10×3.14=314(cm )
圆锥的高:1000×3÷314
教材第91页 第12题
≈10(cm)
答:这个圆锥形铁块的高大约是10cm。
体积不变
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
大正方体的表面积:6×6×6=216(cm )
小正方体的表面积:2×2×6=24(cm )
27个小正方体的表面积的和:24×27=648(cm )
增加的面积:648-216=432(cm )
3×3×3=27(个)答:可以得到27个小正方体。
教材第90页 第11题
答:它们的表面积之和比原来大正方体的表面积增加了432cm 。
6÷2=3
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
教材第90页 第11题
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
2cm
2cm
2cm
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切6次,每次2个大正方形,
一共增加12个大正方形
6×6×12=432(cm )
答:他们的表面积之和比原来大正方体的
表面积增加了432cm 。
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体
半个圆柱
正方体的5个面
圆柱表面积的一半
表面积
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体的5个面
圆柱表面积的一半
表面积
20×20×5=2000(cm )
(2×3.14×10 +20×3.14×20)÷2
=1884÷2
=942(cm )
表面积:2000+942=2942(cm )
答:它的表面积是2942cm 。
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体体积
半个圆柱的体积
体积
体积:8000+3140=11140(cm )
20×20×20=8000(cm )
10×10×3.14×20÷2=3140(cm )
答:它的体积是11140cm 。
面积
表面积
体积
回顾与小结
周长
平行四边形
三角形
梯形
长方形
圆
圆柱
圆锥
长方体
回顾与小结
平面图形
周长
面积
立体图形
表面积
体积
长、宽、底、高、半径……
回顾与小结
透过现象看本质
线
面
体
每行几个
摆几行
共多少个
×
=
长
宽
×
=
长方形面积
现象
本质
推理
抽象
同学们,再见啦
整理和复习——图形的测量
小学六年级 数学
点
线
面
体
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
长度单位
米
分米
厘米
毫米
面积单位
平方米
平方分米
平方厘米
体积单位
立方米
立方分米
立方厘米
10
10
10
100
100
1000
1000
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
周长
封闭图形一周的长度,叫它的周长。
3
1cm
4cm
3cm
5cm
3
+4
+5
=12(cm)
3
两组对边分别相等
C=(a+b )×2
四条边都相等
C=4a
周长和直径的比值是圆周率
C=πd
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
面积
面积
1cm
1cm
5cm
3cm
每行几个
摆几行
共多少个
×
=
长
宽
×
=
长方形面积
长方形面积= 长 × 宽
正方形面积=
边长
边长
S=a
×
a
b
a
S=ab
S=a
先沿高剪开,把三角形向又平移再剪成
可以把平行四边形变成一个长方形
转换成长方形就能计算面积了
平行四边形面积=底×高
S=ah
a
b
a
a
┐
h
S=ab
S=a
S=ah
三角形面积=底×高÷2
S=ah÷2
S=(a+b)÷2
a
b
a
a
┐
h
┐
┐
a
a
b
h
h
S=ab
S=a
S=ah
S=ah÷2
梯形面积公式=(上底+下底)×高÷2
S=(a+b)×h÷2
分割
增补
割补
S=πr
圆的面积=周长的一半×半径
r
a
b
a
a
┐
h
┐
┐
a
a
b
h
h
S=ab
S=a
S=ah
S=ah÷2
S=(a+b)÷2
r
S=πr
需要探索的新图形
转化
学习过的旧图形
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
教材第89页 第4题
每一组中两个图形的周长相等么?面积呢?
周长不相等,面积相等
周长相等,面积不相等
教材第89页 第4题
每一组中两个图形的周长相等么?面积呢?
图形的周长和它的面积大小无关。
教材第90页 第6题
一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
平行四边形面积=底×高
三角形面积=底×高÷2
30÷2=15(cm )
底
高
答:三角形的面积是15cm 。
教材第90页 第6题
一个平行四边形和一个三角形等底等高。已知平行四边形的面积是30cm ,三角形的面积是多少?
平行四边形面积=底×高
三角形面积=底×高÷2
15×2=30(cm )
底
高
答:平行四边形的面积是30cm 。
三角形
的面积是15cm ,平行四边形的面积是多少?
底
高
等底等高的平行四边形和三角形,平行四边形的面积是三角形面积的两倍,三角形的面积是平行四边形面积的二分之一。
等底
等高
三角形面积:15cm
平行四边形面积:30cm
线
面
体
平面图形的周长
平面图形的面积
立体图形的体积
立体图形的表面积
6个面的总面积
3个面的总面积
表面积
图形 面的特点
6个面,相对的面是面积相等的长方形
6个相同的面,每个面都是正方形
长方体表面积=上、下面面积+左、右面面积+前、后面的面积
正方体表面积=每个面的面积×6
S=2ab+2bh+2ah
S=6a
圆柱的表面积=圆柱的侧面面积+两个底面的面积
底面周长×高
S表=Ch+2S底
体积
物体所占空间的大小叫做物体的体积。
8cm
5cm
4cm
1cm
8×4×5=160(cm )
长
宽
高
体积
物体所占空间的大小叫做物体的体积。
长方体所含体积单位的数量就是长方体的体积
长方体的体积正好等于长×宽×高的积
长方体体积=长×宽×高
V=abh
长方体体积=长 × 宽 × 高
=棱长×棱长×棱长
正方体体积
V=a
V=πr h
圆柱体积=底面积×高
S
S
S
h
h
h
V=Sh
圆锥体积等于与它等底等高圆柱体积的三分之一。
V= πr h
1
3
把一个棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高大约是多少?(得数保留整厘米。)
正方体体积=圆锥体积
熔铸
正方体体积:10×10×10=1000(cm )
(圆锥体积)
圆锥的半径:20÷2=10(cm)
圆锥的底面积:10×10×3.14=314(cm )
圆锥的高:1000×3÷314
教材第91页 第12题
≈10(cm)
答:这个圆锥形铁块的高大约是10cm。
体积不变
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
大正方体的表面积:6×6×6=216(cm )
小正方体的表面积:2×2×6=24(cm )
27个小正方体的表面积的和:24×27=648(cm )
增加的面积:648-216=432(cm )
3×3×3=27(个)答:可以得到27个小正方体。
教材第90页 第11题
答:它们的表面积之和比原来大正方体的表面积增加了432cm 。
6÷2=3
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
教材第90页 第11题
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
2cm
2cm
2cm
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
教材第90页 第11题
把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切1次→2个大正方形
切1次→2个大正方形
切2次→4个大正方形
切6次,每次2个大正方形,
一共增加12个大正方形
6×6×12=432(cm )
答:他们的表面积之和比原来大正方体的
表面积增加了432cm 。
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体
半个圆柱
正方体的5个面
圆柱表面积的一半
表面积
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体的5个面
圆柱表面积的一半
表面积
20×20×5=2000(cm )
(2×3.14×10 +20×3.14×20)÷2
=1884÷2
=942(cm )
表面积:2000+942=2942(cm )
答:它的表面积是2942cm 。
这只工具箱的下半部分是棱长为20cm的正方体,上半部分是
圆柱的一半。算出它的表面积和体积。
圆柱的半径:20÷2=10(cm)
教材第91页 第14题
圆柱的高:20cm
正方体体积
半个圆柱的体积
体积
体积:8000+3140=11140(cm )
20×20×20=8000(cm )
10×10×3.14×20÷2=3140(cm )
答:它的体积是11140cm 。
面积
表面积
体积
回顾与小结
周长
平行四边形
三角形
梯形
长方形
圆
圆柱
圆锥
长方体
回顾与小结
平面图形
周长
面积
立体图形
表面积
体积
长、宽、底、高、半径……
回顾与小结
透过现象看本质
线
面
体
每行几个
摆几行
共多少个
×
=
长
宽
×
=
长方形面积
现象
本质
推理
抽象
同学们,再见啦
