8.4机械能守恒定律 (知识小站+例题精析+课堂练兵)(word版含答案)
文档属性
| 名称 | 8.4机械能守恒定律 (知识小站+例题精析+课堂练兵)(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 185.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览


文档简介
高中物理人教版(2019)必修第二册同步讲练测
第八章 机械能守恒定律
8.4机械能守恒定律
知识点1:动能与势能的相互转化
1.机械能:重力势能、弹性势能与动能统称为机械能。
2.表达式:false
3.通过重力或者弹力做功,机械能可以从一种形式转化成另一种形式。
知识点2:机械能守恒定律
1.基本内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
2.机械能守恒定律的三种常见表达式
①守恒观点:表达式为false,系统的初状态机械能的总和与末状态机械能的总和相等。
②转化的观点:表达式为false,系统机械能守恒时,系统减少(或增加)的重力势能等于系统增加(或减少)的动能。
③转移的观点:表达式为false,如果系统由A、B两部分组成,则A部分物体机械能的增加量与B部分物体机械能的减少量相等。
知识点3:守恒条件:只有重力或系统内弹力做功;机械能守恒是指整个过程中系统机械能始终不变,而不仅仅是指初状态与末状态的机械能相等。
例1.质量为25kg的小孩坐在秋千上,如果秋千摆到最高点时,绳子与竖直方向的夹角是60°,秋千板摆到最低点时,忽略手与绳间的作用力,求小孩对秋千板的压力大小。(不考虑摩擦及空气阻力,g取10m/s2)
【解析】 解;秋千从最高点摆到最低点过程中,只有重力做功,机械能守恒,则 mgl(1?cos60°)=12mv2
在最低点时,设秋千对小孩的支持力为FN , 由牛顿第二定律得 FN?mg=mv2l
解得 FN=500N
由牛顿第三定律得小孩对秋千板的压力大小为500N。
例2.某海湾共占面积1.0×106m2 , 涨潮时水深20m,若利用这个海湾修建一座水坝,此时关上水坝的闸门时,可使水位保持20m不变。退潮时,坝外水位降至18m。假如利用此水坝建水力发电站,已知重力势能转化为电能的效率是10%,每天有两次涨潮,涨潮和退潮时水流都推动水轮机发电,试估算该电站一天能发多少电能?重力加速度g取10m/s2。海水密度近似为1.0×103kg/m3。
【解析】 解:一次涨潮水的质量 m=S×Δ?×ρ
一次涨潮水的重力势能变化 ΔEp=mgΔ?2
一次涨潮水的重力势能转化为电能 ΔE电=ΔEp×10%
电站一天能发电能 E电=ΔE电×4=8.0×109J
1.一质量为m的物块仅在重力作用下运动,物块位于r1和r2时的重力势能分别为3E0和E0(E0>0)。若物块位于r1时速度为0,则位于r2时其速度大小为(?? )
A.?2E0m????????????????????????????????B.?6E0m????????????????????????????????C.?22E0m????????????????????????????????D.?4E0m
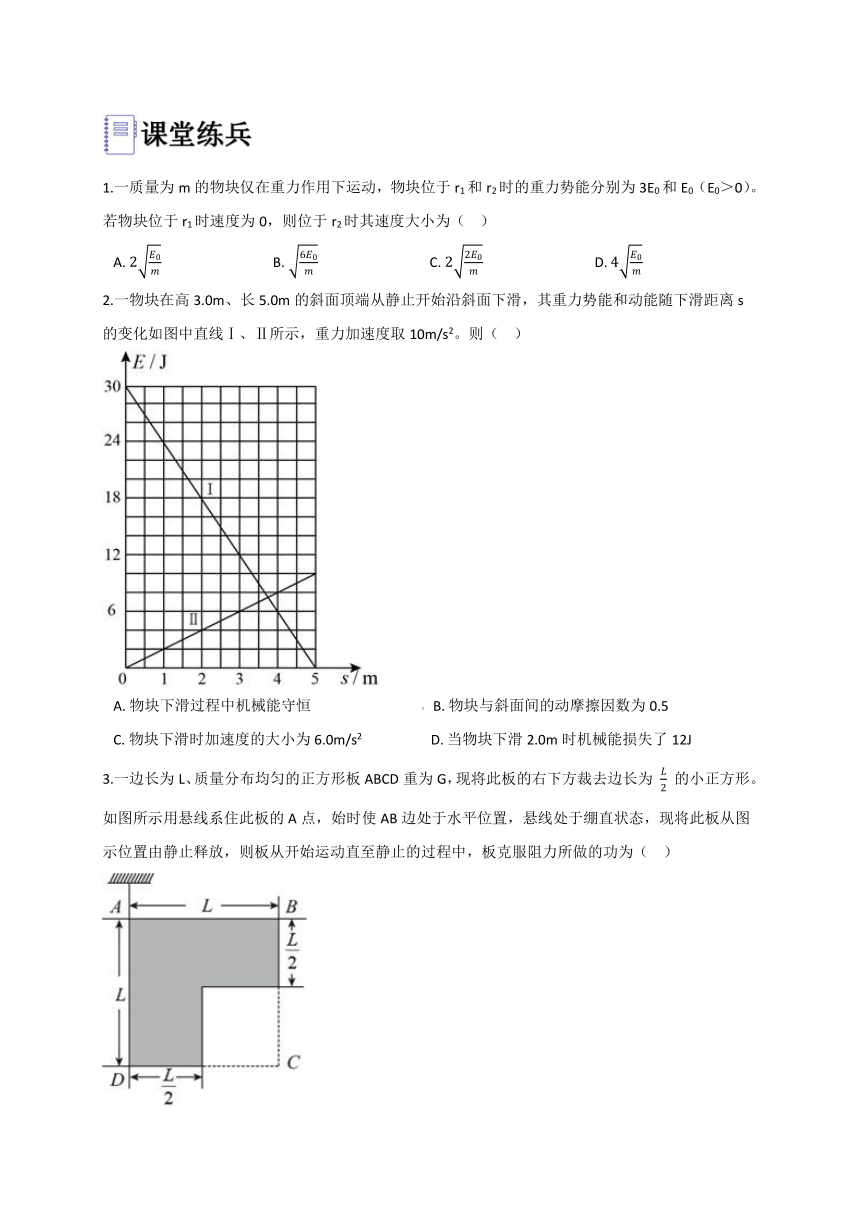
2.一物块在高3.0m、长5.0m的斜面顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示,重力加速度取10m/s2。则(?? )
A.?物块下滑过程中机械能守恒???????????????????????????????? B.?物块与斜面间的动摩擦因数为0.5
C.?物块下滑时加速度的大小为6.0m/s2????????????????????D.?当物块下滑2.0m时机械能损失了12J
3.一边长为L、质量分布均匀的正方形板ABCD重为G,现将此板的右下方裁去边长为 L2 的小正方形。如图所示用悬线系住此板的A点,始时使AB边处于水平位置,悬线处于绷直状态,现将此板从图示位置由静止释放,则板从开始运动直至静止的过程中,板克服阻力所做的功为(?? )
A.?(22?12)GL????????????????B.?(24?14)GL????????????????C.?(528?58)GL????????????????D.?(5216?516)GL
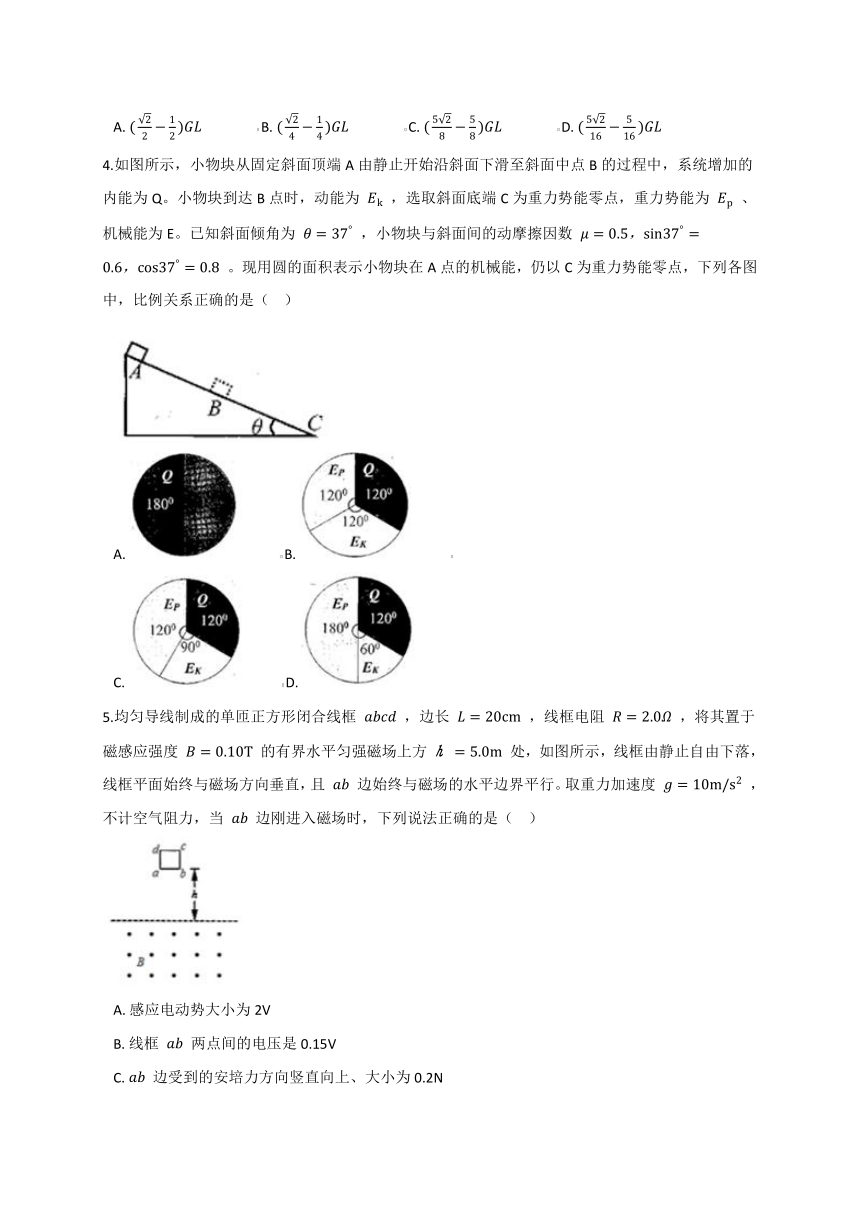
4.如图所示,小物块从固定斜面顶端A由静止开始沿斜面下滑至斜面中点B的过程中,系统增加的内能为Q。小物块到达B点时,动能为 Ek ,选取斜面底端C为重力势能零点,重力势能为 Ep 、机械能为E。已知斜面倾角为 θ=37° ,小物块与斜面间的动摩擦因数 μ=0.5,sin37°=0.6,cos37°=0.8 。现用圆的面积表示小物块在A点的机械能,仍以C为重力势能零点,下列各图中,比例关系正确的是(?? )
A.????????????B.????????????
C.????????????D.?
5.均匀导线制成的单匝正方形闭合线框 abcd ,边长 L=20cm ,线框电阻 R=2.0Ω ,将其置于磁感应强度 B=0.10T 的有界水平匀强磁场上方 ?=5.0m 处,如图所示,线框由静止自由下落,线框平面始终与磁场方向垂直,且 ab 边始终与磁场的水平边界平行。取重力加速度 g=10m/s2 ,不计空气阻力,当 ab 边刚进入磁场时,下列说法正确的是(?? )
A.?感应电动势大小为2V
B.?线框 ab 两点间的电压是0.15V
C.?ab 边受到的安培力方向竖直向上、大小为0.2N
D.?线框全部进入磁场的过程中,通过导线横截面的电荷量为0.2C
6.一物块在高 3.0m 、长 5.0m 的斜面顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示,取 g=10m/s2 。则物块开始下滑 2m 过程中,机械能损失________ J ;物块沿斜面下滑的加速度 a= ________ m/s2 。
7.如图所示,光滑轨道 abc 固定在竖直平面内形成一重力势阱,两侧高分别为 H1 和 H2 。可视为质点的小物块 Q 质量为 m ,静置于水平轨道 b 处。设重力加速度为 g ;若以 a 处所在平面为重力势能零势能面,物块 Q 在 b 处机械能为________,一质量为 m 的小球 P 从 a 处静止落下,在 b 处与滑块 Q 相撞后小球 P 将动能全部传给滑块 Q ,随后滑块 Q 从陷阱右侧滑出,其到达 c 处的速度 v 大小为________。
参考答案
1.【答案】 A
【解析】物体仅在重力作用下运动,物体的机械能守恒,根据机械能守恒定律可知 E1=E2
代入已知条件为 3E0+0=E0+12mv2
解得 r2 处的速度为 v=2E0m
故答案为:A。
2.【答案】 B
【解析】A.下滑5m的过程中,重力势能减少30J,动能增加10J,减小的重力势能并不等于增加的动能,所以机械能不守恒,A不符合题意;
B.斜面高3m、长5m,则斜面倾角为θ=37°。令斜面底端为零势面,则物块在斜面顶端时的重力势能mgh=30J
可得质量m=1kg
下滑5m过程中,由功能原理,机械能的减少量等于克服摩擦力做的功μmg·cosθ·s=20J
求得μ=0.5
B符合题意;
C.由牛顿第二定律mgsinθ-μmgcosθ=ma
求得a=2m/s2
C不符合题意;
D.物块下滑2.0m时,重力势能减少12J,动能增加4J,所以机械能损失了8J,D不符合题意。
故答案为:B。
3.【答案】 D
【解析】如图所示:设将板的右下方裁去边长为 L2 的小正方形后,板的重心在AO的连线上点E处,由杠杆平衡原理可知 34G×OE=24L×14G
解得: OE=212L
将此板从图示位置由静止释放,则板从开始运动直至静止的过程中,重心下降的高度为 ?=AE?EG=(1?22)AE=(1?22)(22?212)L=(5212?512)L
由能量守恒定律可知,板克服阻力所做的功等于板减小的重力势能,为 ΔEp=34G?=34G×(5212?512)L=(5216?516)GL
故答案为:D。
4.【答案】 D
【解析】设斜面的长度为 L ,物块的质量为 m ,小物块开始运动时的机械能等于小物块在 A 点的重力势能,则有 E=mgLsinθ=0.6mgL
小物块在 B 点时的重力势能为 Ep=mg?L2sinθ=E2
此过程中克服摩擦力做的功等于产生的热量,则有 Q=μmgcosθ×L2=0.2mgL=E3
根据功能关系可得 Ek=E?Ep?Q=E?E2?E3=E6
若用圆的面积表示小物块在 A 点的机械能,则重力势能占总面积的 12 ,产生热量占总面积的 13 ,动能占总面积的 16 ,D符合题意,ABC不符合题意。
故答案为:D。
5.【答案】 B
【解析】A.设线框ab刚进磁场时的速度为v,根据机械能守恒定律得 mg?=12mv2 ,解得: v=2g?=10m/s
感应电动势E=BLv=0.2V
A不符合题意;
B.由闭合电路欧姆定律可知,线框ab两点间的电压 Uab=34E=34×0.2V=0.15V
B符合题意;
C.电流 I=ER=0.22A=0.1A
由左手定则可知,ab边受到的安培力方向向上,大小为 F=BIL=0.10×0.1×0.20N=0.002N
C不符合题意;
D.线框全部进入磁场的过程中,通过导线横截面的电荷量为 q=BL2R=0.002C
D不符合题意。
故答案为:B。
6.【答案】 8;2
【解析】由图像可知,物块下滑2m过程中,重力势能减少量为 ΔEp=30J?18J=12J
动能的增加量为 ΔEk=4J?0=4J
故此过程中,机械能的损失为 ΔE=12J?4J=8J 物块机械能的减少量等于克服阻力所做的功,故物块下滑2m过程中,克服阻力做功8J,动能增加量等于合力所做的功,故此过程中,合力做功为4J,由此可知 mgssinθ?fs=4J,fs=8J
解得 f=23mgsinθ
其中 sinθ=3.0m5.0m=0.6
由牛顿第二定律,有 mgsinθ?f=ma
解得 a=13gsinθ=13×10×0.6m/s2=2m/s2
7.【答案】 ?mgH1;2g(H1?H2)
【解析】以 a 处所在平面为重力势能零势能面,则物块 Q 在 b 处的重力势能为 EP=?mgH1
又因为物块 Q 质量为 m ,静置于水平轨道 b 处,则物块 Q 在 b 处的动能为 Ek=0
因此物块 Q 在 b 处机械能为 E=EP+Ek=?mgH1 由题可知,整个过程满足机械能守恒,则有 0=?mg(H1?H2)+12mvc2
解得,物块 Q 到达 c 处的速度 v 大小为 vc=2g(H1?H2)
第八章 机械能守恒定律
8.4机械能守恒定律
知识点1:动能与势能的相互转化
1.机械能:重力势能、弹性势能与动能统称为机械能。
2.表达式:false
3.通过重力或者弹力做功,机械能可以从一种形式转化成另一种形式。
知识点2:机械能守恒定律
1.基本内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
2.机械能守恒定律的三种常见表达式
①守恒观点:表达式为false,系统的初状态机械能的总和与末状态机械能的总和相等。
②转化的观点:表达式为false,系统机械能守恒时,系统减少(或增加)的重力势能等于系统增加(或减少)的动能。
③转移的观点:表达式为false,如果系统由A、B两部分组成,则A部分物体机械能的增加量与B部分物体机械能的减少量相等。
知识点3:守恒条件:只有重力或系统内弹力做功;机械能守恒是指整个过程中系统机械能始终不变,而不仅仅是指初状态与末状态的机械能相等。
例1.质量为25kg的小孩坐在秋千上,如果秋千摆到最高点时,绳子与竖直方向的夹角是60°,秋千板摆到最低点时,忽略手与绳间的作用力,求小孩对秋千板的压力大小。(不考虑摩擦及空气阻力,g取10m/s2)
【解析】 解;秋千从最高点摆到最低点过程中,只有重力做功,机械能守恒,则 mgl(1?cos60°)=12mv2
在最低点时,设秋千对小孩的支持力为FN , 由牛顿第二定律得 FN?mg=mv2l
解得 FN=500N
由牛顿第三定律得小孩对秋千板的压力大小为500N。
例2.某海湾共占面积1.0×106m2 , 涨潮时水深20m,若利用这个海湾修建一座水坝,此时关上水坝的闸门时,可使水位保持20m不变。退潮时,坝外水位降至18m。假如利用此水坝建水力发电站,已知重力势能转化为电能的效率是10%,每天有两次涨潮,涨潮和退潮时水流都推动水轮机发电,试估算该电站一天能发多少电能?重力加速度g取10m/s2。海水密度近似为1.0×103kg/m3。
【解析】 解:一次涨潮水的质量 m=S×Δ?×ρ
一次涨潮水的重力势能变化 ΔEp=mgΔ?2
一次涨潮水的重力势能转化为电能 ΔE电=ΔEp×10%
电站一天能发电能 E电=ΔE电×4=8.0×109J
1.一质量为m的物块仅在重力作用下运动,物块位于r1和r2时的重力势能分别为3E0和E0(E0>0)。若物块位于r1时速度为0,则位于r2时其速度大小为(?? )
A.?2E0m????????????????????????????????B.?6E0m????????????????????????????????C.?22E0m????????????????????????????????D.?4E0m
2.一物块在高3.0m、长5.0m的斜面顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示,重力加速度取10m/s2。则(?? )
A.?物块下滑过程中机械能守恒???????????????????????????????? B.?物块与斜面间的动摩擦因数为0.5
C.?物块下滑时加速度的大小为6.0m/s2????????????????????D.?当物块下滑2.0m时机械能损失了12J
3.一边长为L、质量分布均匀的正方形板ABCD重为G,现将此板的右下方裁去边长为 L2 的小正方形。如图所示用悬线系住此板的A点,始时使AB边处于水平位置,悬线处于绷直状态,现将此板从图示位置由静止释放,则板从开始运动直至静止的过程中,板克服阻力所做的功为(?? )
A.?(22?12)GL????????????????B.?(24?14)GL????????????????C.?(528?58)GL????????????????D.?(5216?516)GL
4.如图所示,小物块从固定斜面顶端A由静止开始沿斜面下滑至斜面中点B的过程中,系统增加的内能为Q。小物块到达B点时,动能为 Ek ,选取斜面底端C为重力势能零点,重力势能为 Ep 、机械能为E。已知斜面倾角为 θ=37° ,小物块与斜面间的动摩擦因数 μ=0.5,sin37°=0.6,cos37°=0.8 。现用圆的面积表示小物块在A点的机械能,仍以C为重力势能零点,下列各图中,比例关系正确的是(?? )
A.????????????B.????????????
C.????????????D.?
5.均匀导线制成的单匝正方形闭合线框 abcd ,边长 L=20cm ,线框电阻 R=2.0Ω ,将其置于磁感应强度 B=0.10T 的有界水平匀强磁场上方 ?=5.0m 处,如图所示,线框由静止自由下落,线框平面始终与磁场方向垂直,且 ab 边始终与磁场的水平边界平行。取重力加速度 g=10m/s2 ,不计空气阻力,当 ab 边刚进入磁场时,下列说法正确的是(?? )
A.?感应电动势大小为2V
B.?线框 ab 两点间的电压是0.15V
C.?ab 边受到的安培力方向竖直向上、大小为0.2N
D.?线框全部进入磁场的过程中,通过导线横截面的电荷量为0.2C
6.一物块在高 3.0m 、长 5.0m 的斜面顶端从静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示,取 g=10m/s2 。则物块开始下滑 2m 过程中,机械能损失________ J ;物块沿斜面下滑的加速度 a= ________ m/s2 。
7.如图所示,光滑轨道 abc 固定在竖直平面内形成一重力势阱,两侧高分别为 H1 和 H2 。可视为质点的小物块 Q 质量为 m ,静置于水平轨道 b 处。设重力加速度为 g ;若以 a 处所在平面为重力势能零势能面,物块 Q 在 b 处机械能为________,一质量为 m 的小球 P 从 a 处静止落下,在 b 处与滑块 Q 相撞后小球 P 将动能全部传给滑块 Q ,随后滑块 Q 从陷阱右侧滑出,其到达 c 处的速度 v 大小为________。
参考答案
1.【答案】 A
【解析】物体仅在重力作用下运动,物体的机械能守恒,根据机械能守恒定律可知 E1=E2
代入已知条件为 3E0+0=E0+12mv2
解得 r2 处的速度为 v=2E0m
故答案为:A。
2.【答案】 B
【解析】A.下滑5m的过程中,重力势能减少30J,动能增加10J,减小的重力势能并不等于增加的动能,所以机械能不守恒,A不符合题意;
B.斜面高3m、长5m,则斜面倾角为θ=37°。令斜面底端为零势面,则物块在斜面顶端时的重力势能mgh=30J
可得质量m=1kg
下滑5m过程中,由功能原理,机械能的减少量等于克服摩擦力做的功μmg·cosθ·s=20J
求得μ=0.5
B符合题意;
C.由牛顿第二定律mgsinθ-μmgcosθ=ma
求得a=2m/s2
C不符合题意;
D.物块下滑2.0m时,重力势能减少12J,动能增加4J,所以机械能损失了8J,D不符合题意。
故答案为:B。
3.【答案】 D
【解析】如图所示:设将板的右下方裁去边长为 L2 的小正方形后,板的重心在AO的连线上点E处,由杠杆平衡原理可知 34G×OE=24L×14G
解得: OE=212L
将此板从图示位置由静止释放,则板从开始运动直至静止的过程中,重心下降的高度为 ?=AE?EG=(1?22)AE=(1?22)(22?212)L=(5212?512)L
由能量守恒定律可知,板克服阻力所做的功等于板减小的重力势能,为 ΔEp=34G?=34G×(5212?512)L=(5216?516)GL
故答案为:D。
4.【答案】 D
【解析】设斜面的长度为 L ,物块的质量为 m ,小物块开始运动时的机械能等于小物块在 A 点的重力势能,则有 E=mgLsinθ=0.6mgL
小物块在 B 点时的重力势能为 Ep=mg?L2sinθ=E2
此过程中克服摩擦力做的功等于产生的热量,则有 Q=μmgcosθ×L2=0.2mgL=E3
根据功能关系可得 Ek=E?Ep?Q=E?E2?E3=E6
若用圆的面积表示小物块在 A 点的机械能,则重力势能占总面积的 12 ,产生热量占总面积的 13 ,动能占总面积的 16 ,D符合题意,ABC不符合题意。
故答案为:D。
5.【答案】 B
【解析】A.设线框ab刚进磁场时的速度为v,根据机械能守恒定律得 mg?=12mv2 ,解得: v=2g?=10m/s
感应电动势E=BLv=0.2V
A不符合题意;
B.由闭合电路欧姆定律可知,线框ab两点间的电压 Uab=34E=34×0.2V=0.15V
B符合题意;
C.电流 I=ER=0.22A=0.1A
由左手定则可知,ab边受到的安培力方向向上,大小为 F=BIL=0.10×0.1×0.20N=0.002N
C不符合题意;
D.线框全部进入磁场的过程中,通过导线横截面的电荷量为 q=BL2R=0.002C
D不符合题意。
故答案为:B。
6.【答案】 8;2
【解析】由图像可知,物块下滑2m过程中,重力势能减少量为 ΔEp=30J?18J=12J
动能的增加量为 ΔEk=4J?0=4J
故此过程中,机械能的损失为 ΔE=12J?4J=8J 物块机械能的减少量等于克服阻力所做的功,故物块下滑2m过程中,克服阻力做功8J,动能增加量等于合力所做的功,故此过程中,合力做功为4J,由此可知 mgssinθ?fs=4J,fs=8J
解得 f=23mgsinθ
其中 sinθ=3.0m5.0m=0.6
由牛顿第二定律,有 mgsinθ?f=ma
解得 a=13gsinθ=13×10×0.6m/s2=2m/s2
7.【答案】 ?mgH1;2g(H1?H2)
【解析】以 a 处所在平面为重力势能零势能面,则物块 Q 在 b 处的重力势能为 EP=?mgH1
又因为物块 Q 质量为 m ,静置于水平轨道 b 处,则物块 Q 在 b 处的动能为 Ek=0
因此物块 Q 在 b 处机械能为 E=EP+Ek=?mgH1 由题可知,整个过程满足机械能守恒,则有 0=?mg(H1?H2)+12mvc2
解得,物块 Q 到达 c 处的速度 v 大小为 vc=2g(H1?H2)
