北师大版数学八年级下册:1.3 线段的垂直平分线 同步练习(word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册:1.3 线段的垂直平分线 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览



文档简介
3 线段的垂直平分线
第1课时 线段垂直平分线的性质定理及其逆定理
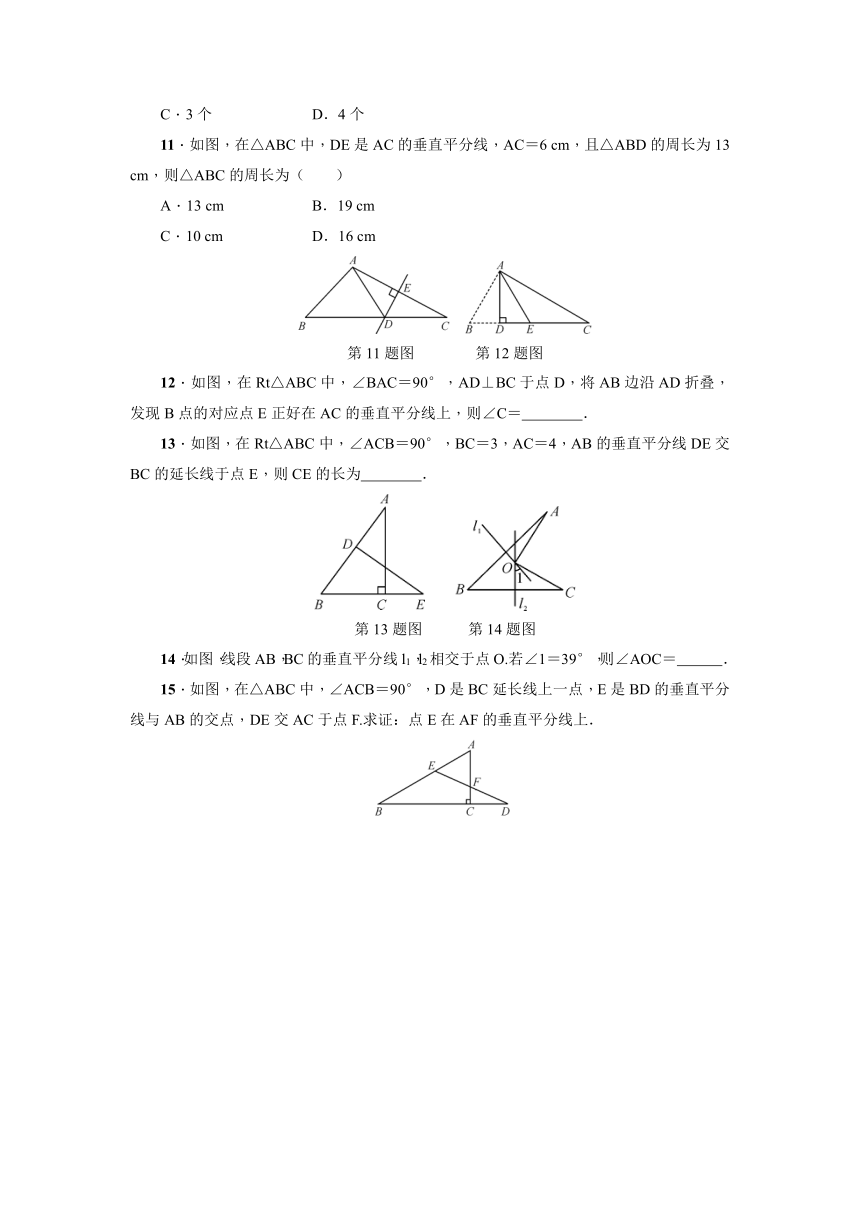
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为( )
A.6 cm B.5 cm
C.4 cm D.3 cm
第1题图 第2题图
2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11
C.16 D.17
第3题图 第4题图
4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为 .
5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
6.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
第6题图 第7题图
7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是( )
A.P是AC的垂直平分线与AB的交点
B.P是BC的垂直平分线与AB的交点
C.P是∠ACB的平分线与AB的交点
D.P是以点B为圆心,AC长为半径的弧与边AB的交点
8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.
9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为 .
10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
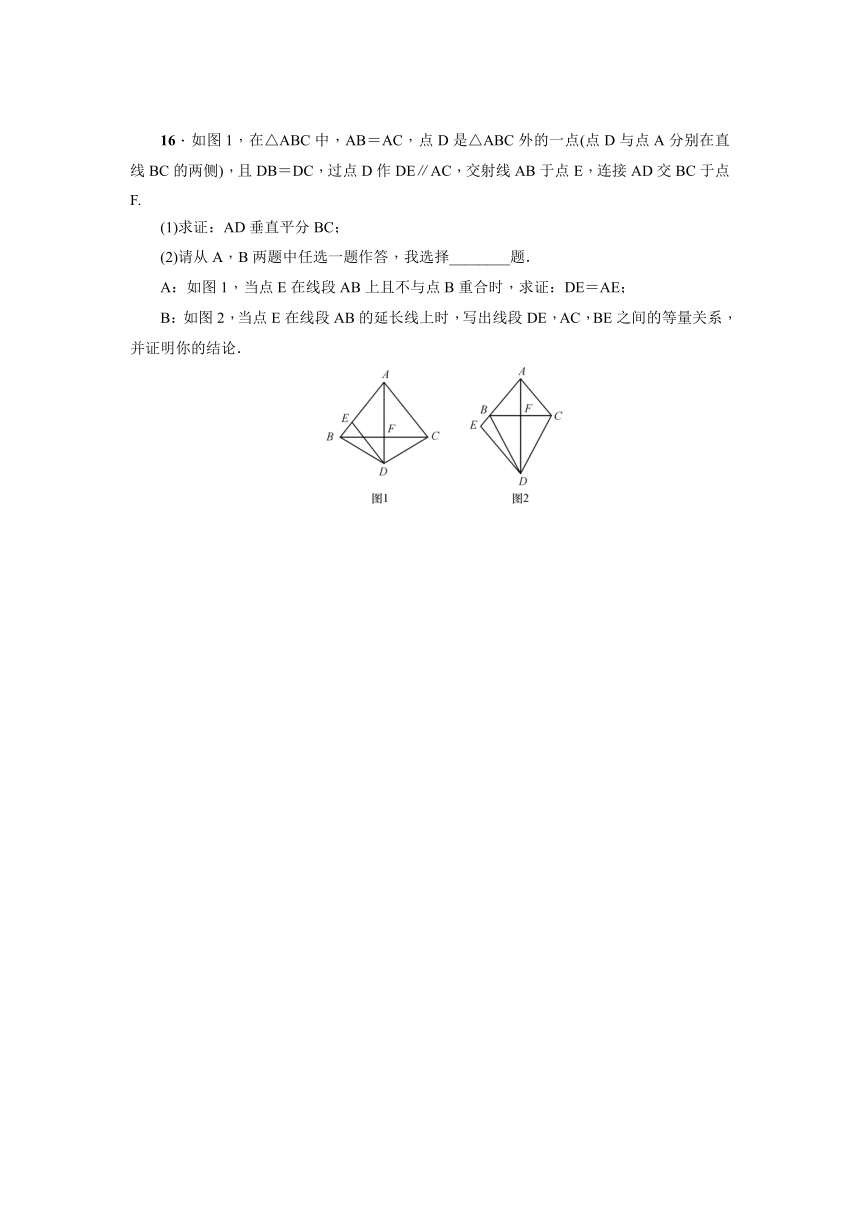
11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为( )
A.13 cm B.19 cm
C.10 cm D.16 cm
第11题图 第12题图
12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C= .
13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为 .
第13题图 第14题图
14.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC= .
15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.
16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择________题.
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.
第2课时 三角形三边的垂直平分线
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条中线的交点
B.三条角平分线的交点
C.三条边的垂直平分线的交点
D.三条高的交点
3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是( )
A.锐角三角形 B.钝角三角形
C.等边三角形 D.直角三角形
4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在( )
23133050A.直线MN上
B.直线MN的左侧
C.直线MN的右侧
D.直线MN的左侧或右侧
5.下列作图语句正确的是( )
A.过点P作线段AB的垂直平分线
B.在线段AB的延长线上取一点C,使AB=AC
C.过直线a和直线b外一点P作直线MN,使MN∥a∥b
D.过点P作直线AB的垂线
6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
第6题图 第7题图
7.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,BC交于点D,E,连接AE,则:
(1)∠ADE= ;
(2)AE EC;(填“=”“>”或“<”)
(3)当AB=3,AC=5时,△ABE的周长等于 .
1985645981075B村
·
B村
·
8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇A村、B村、C村所属的村委会所在地的距离都相等(A,B,C不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作,不写作法,保留作图痕迹.
2473325124460C村
·
C村
·
111696540640A村
·
A村
·
9.在平面内,到三点A,B,C距离相等的点( )
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;
②作直线MN,与边AB相交于点D,连接CD.
下列说法不一定正确的是( )
A.∠BDN=∠CDN B.∠ADC=2∠B
C.∠ACD=∠DCB D.2∠B+∠ACD=90°
11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则( )
A.点P在三角形内
B.点P在三角形外
C.点P在三角形底边上
D.点P的位置与三角形的边长有关
12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案 .
13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).
14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=120°,求∠MCN的度数;
(2)若△CMN的周长为15 cm,求AB的长;
(3)若∠MFN=70°,求∠MCN的度数.
【变式】 如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数;
(2)若△APQ周长为12,BC长为8,求PQ的长.
参考答案:
第1课时 线段垂直平分线的性质定理及其逆定理
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为(D)
A.6 cm B.5 cm
C.4 cm D.3 cm
第1题图 第2题图
2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是(B)
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC=5,则△ACE的周长为(B)
A.8 B.11
C.16 D.17
第3题图 第4题图
4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为30°.
5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
证明:∵DE是AB的垂直平分线,
∴EA=EB.
∴∠EAB=∠B.
∵∠C=90°,
∴∠CAB+∠B=90°.
又∵∠AED+∠EAB=90°,
∴∠CAB=∠AED.
6.如图,AC=AD,BC=BD,则有(A)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
第6题图 第7题图
7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是(B)
A.P是AC的垂直平分线与AB的交点
B.P是BC的垂直平分线与AB的交点
C.P是∠ACB的平分线与AB的交点
D.P是以点B为圆心,AC长为半径的弧与边AB的交点
8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.
证明:∵∠C=90°,∠A=30°,
∴∠ABC=90°-30°=60°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=30°.
∴∠A=∠ABD.
∴DA=DB.
∴点D在AB的垂直平分线上.
9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为20°或70°.
10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有(C)
A.1个 B.2个
C.3个 D.4个
11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为(B)
A.13 cm B.19 cm
C.10 cm D.16 cm
第11题图 第12题图
12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=30°.
13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为.
第13题图 第14题图
14.(2020·南京)如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC=78°.
15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.
证明:∵E是BD的垂直平分线上的一点,
∴EB=ED.
∴∠B=∠D.
∵∠ACB=90°,
∴∠A=90°-∠B,∠CFD=90°-∠D.
∴∠CFD=∠A.
又∵∠AFE=∠CFD,
∴∠AFE=∠A.
∴EF=EA.
∴点E在AF的垂直平分线上.
16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择________题.
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.
解:(1)证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵DB=DC,
∴点D在线段BC的垂直平分线上.
∴AD垂直平分BC.
(2)选择A,证明:
由(1),得AD⊥BC,
又∵AB=AC,∴∠BAF=∠CAF.
∵DE∥AC,∴∠CAF=∠ADE.
∴∠BAF=∠ADE.
∴DE=AE.
选择B,线段DE,AC,BE之间的等量关系为DE=BE+AC.
证明:由(1),得AF⊥BC,
又∵AB=AC,∴∠BAF=∠CAF.
∵DE∥AC,∴∠EDA=∠CAF.
∴∠BAF=∠EDA.
∴AE=DE.
∵AE=EB+AB,AB=AC,
∴DE=BE+AC.
第2课时 三角形三边的垂直平分线
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定(D)
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形(C)
A.三条中线的交点
B.三条角平分线的交点
C.三条边的垂直平分线的交点
D.三条高的交点
3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是(D)
A.锐角三角形 B.钝角三角形
C.等边三角形 D.直角三角形
4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在(A)
A.直线MN上
B.直线MN的左侧
C.直线MN的右侧
D.直线MN的左侧或右侧
5.下列作图语句正确的是(D)
A.过点P作线段AB的垂直平分线
B.在线段AB的延长线上取一点C,使AB=AC
C.过直线a和直线b外一点P作直线MN,使MN∥a∥b
D.过点P作直线AB的垂线
6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
第6题图 第7题图
7.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,BC交于点D,E,连接AE,则:
(1)∠ADE=90°;
(2)AE=EC;(填“=”“>”或“<”)
(3)当AB=3,AC=5时,△ABE的周长等于7.
8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇A村、B村、C村所属的村委会所在地的距离都相等(A,B,C不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作,不写作法,保留作图痕迹.
解:已知:A,B,C三点不在同一直线上.
求作:作一点P,使PA=PB=PC.
如图所示,点P即为所求的点.
9.在平面内,到三点A,B,C距离相等的点(D)
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;
②作直线MN,与边AB相交于点D,连接CD.
下列说法不一定正确的是(C)
A.∠BDN=∠CDN B.∠ADC=2∠B
C.∠ACD=∠DCB D.2∠B+∠ACD=90°
11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则(B)
A.点P在三角形内
B.点P在三角形外
C.点P在三角形底边上
D.点P的位置与三角形的边长有关
12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案③.
13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).
解:作法:(1)作线段AD=a;
(2)过点D作直线MN⊥AD于点D;
(3)以点A为圆心,b为半径画弧,交MN于B,C两点,连接AB,AC,△ABC即为所求,如图所示.
14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=120°,求∠MCN的度数;
(2)若△CMN的周长为15 cm,求AB的长;
(3)若∠MFN=70°,求∠MCN的度数.
解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,CN=BN.
∴∠A=∠ACM,∠B=∠BCN.
∴∠MCN=180°-(∠CMN+∠CNM)
=180°-(2∠A+2∠B)
=180°-2(180°-∠ACB)
=60°.
(2)∵AM=CM,BN=CN,∴△CMN的周长为CM+MN+CN=AM+MN+BN=AB.
∵△CMN的周长为15 cm,∴AB=15 cm.
(3)∵∠MFN=70°,
∴∠MNF+∠NMF=180°-70°=110°.
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠NMF+∠MNF=110°.
∴∠A+∠B=90°-∠AMD+90°-∠BNE=70°.
又∵∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=40°.
【变式】 如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数;
(2)若△APQ周长为12,BC长为8,求PQ的长.
解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ.
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y.
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°.
∴x=20°.
∴∠PAQ=20°.
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12.
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,即BC+2PQ=12.
∵BC=8,
∴PQ=2.
第1课时 线段垂直平分线的性质定理及其逆定理
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为( )
A.6 cm B.5 cm
C.4 cm D.3 cm
第1题图 第2题图
2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是( )
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC=5,则△ACE的周长为( )
A.8 B.11
C.16 D.17
第3题图 第4题图
4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为 .
5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
6.如图,AC=AD,BC=BD,则有( )
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
第6题图 第7题图
7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是( )
A.P是AC的垂直平分线与AB的交点
B.P是BC的垂直平分线与AB的交点
C.P是∠ACB的平分线与AB的交点
D.P是以点B为圆心,AC长为半径的弧与边AB的交点
8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.
9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为 .
10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为( )
A.13 cm B.19 cm
C.10 cm D.16 cm
第11题图 第12题图
12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C= .
13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为 .
第13题图 第14题图
14.如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC= .
15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.
16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择________题.
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.
第2课时 三角形三边的垂直平分线
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定( )
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A.三条中线的交点
B.三条角平分线的交点
C.三条边的垂直平分线的交点
D.三条高的交点
3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是( )
A.锐角三角形 B.钝角三角形
C.等边三角形 D.直角三角形
4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在( )
23133050A.直线MN上
B.直线MN的左侧
C.直线MN的右侧
D.直线MN的左侧或右侧
5.下列作图语句正确的是( )
A.过点P作线段AB的垂直平分线
B.在线段AB的延长线上取一点C,使AB=AC
C.过直线a和直线b外一点P作直线MN,使MN∥a∥b
D.过点P作直线AB的垂线
6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是( )
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
第6题图 第7题图
7.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,BC交于点D,E,连接AE,则:
(1)∠ADE= ;
(2)AE EC;(填“=”“>”或“<”)
(3)当AB=3,AC=5时,△ABE的周长等于 .
1985645981075B村
·
B村
·
8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇A村、B村、C村所属的村委会所在地的距离都相等(A,B,C不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作,不写作法,保留作图痕迹.
2473325124460C村
·
C村
·
111696540640A村
·
A村
·
9.在平面内,到三点A,B,C距离相等的点( )
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;
②作直线MN,与边AB相交于点D,连接CD.
下列说法不一定正确的是( )
A.∠BDN=∠CDN B.∠ADC=2∠B
C.∠ACD=∠DCB D.2∠B+∠ACD=90°
11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则( )
A.点P在三角形内
B.点P在三角形外
C.点P在三角形底边上
D.点P的位置与三角形的边长有关
12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案 .
13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).
14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=120°,求∠MCN的度数;
(2)若△CMN的周长为15 cm,求AB的长;
(3)若∠MFN=70°,求∠MCN的度数.
【变式】 如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数;
(2)若△APQ周长为12,BC长为8,求PQ的长.
参考答案:
第1课时 线段垂直平分线的性质定理及其逆定理
1.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点.已知线段PA=3 cm,则线段PB的长为(D)
A.6 cm B.5 cm
C.4 cm D.3 cm
第1题图 第2题图
2.如图,AB是CD的垂直平分线.若AC=2.3 cm,BD=1.6 cm,则四边形ACBD的周长是(B)
A.3.9 cm B.7.8 cm
C.4 cm D.4.6 cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E.若BC=6,AC=5,则△ACE的周长为(B)
A.8 B.11
C.16 D.17
第3题图 第4题图
4.如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB.若∠A=50°,则∠B的度数为30°.
5.如图,在Rt△ABC中,∠C=90°,AB边的垂直平分线DE交BC于点E,垂足为D.求证:∠CAB=∠AED.
证明:∵DE是AB的垂直平分线,
∴EA=EB.
∴∠EAB=∠B.
∵∠C=90°,
∴∠CAB+∠B=90°.
又∵∠AED+∠EAB=90°,
∴∠CAB=∠AED.
6.如图,AC=AD,BC=BD,则有(A)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
第6题图 第7题图
7.如图,已知△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB.下列描述正确的是(B)
A.P是AC的垂直平分线与AB的交点
B.P是BC的垂直平分线与AB的交点
C.P是∠ACB的平分线与AB的交点
D.P是以点B为圆心,AC长为半径的弧与边AB的交点
8.如图,在△ABC中,∠C=90°,∠A=30°,BD平分∠ABC交AC于点D.求证:点D在AB的垂直平分线上.
证明:∵∠C=90°,∠A=30°,
∴∠ABC=90°-30°=60°.
∵BD平分∠ABC,
∴∠ABD=∠ABC=30°.
∴∠A=∠ABD.
∴DA=DB.
∴点D在AB的垂直平分线上.
9.在△ABC中,AB=AC,边AB的垂直平分线与边AC所在的直线相交所得的锐角为50°,则∠C的度数为20°或70°.
10.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB;②若PA=PB,EA=EB,则直线PE是线段AB的垂直平分线;③若EA=EB,则直线EP是线段AB的垂直平分线;④若PA=PB,则点P在线段AB的垂直平分线上.其中正确的有(C)
A.1个 B.2个
C.3个 D.4个
11.如图,在△ABC中,DE是AC的垂直平分线,AC=6 cm,且△ABD的周长为13 cm,则△ABC的周长为(B)
A.13 cm B.19 cm
C.10 cm D.16 cm
第11题图 第12题图
12.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=30°.
13.如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,AB的垂直平分线DE交BC的延长线于点E,则CE的长为.
第13题图 第14题图
14.(2020·南京)如图,线段AB,BC的垂直平分线l1,l2相交于点O.若∠1=39°,则∠AOC=78°.
15.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是BD的垂直平分线与AB的交点,DE交AC于点F.求证:点E在AF的垂直平分线上.
证明:∵E是BD的垂直平分线上的一点,
∴EB=ED.
∴∠B=∠D.
∵∠ACB=90°,
∴∠A=90°-∠B,∠CFD=90°-∠D.
∴∠CFD=∠A.
又∵∠AFE=∠CFD,
∴∠AFE=∠A.
∴EF=EA.
∴点E在AF的垂直平分线上.
16.如图1,在△ABC中,AB=AC,点D是△ABC外的一点(点D与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择________题.
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.
解:(1)证明:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵DB=DC,
∴点D在线段BC的垂直平分线上.
∴AD垂直平分BC.
(2)选择A,证明:
由(1),得AD⊥BC,
又∵AB=AC,∴∠BAF=∠CAF.
∵DE∥AC,∴∠CAF=∠ADE.
∴∠BAF=∠ADE.
∴DE=AE.
选择B,线段DE,AC,BE之间的等量关系为DE=BE+AC.
证明:由(1),得AF⊥BC,
又∵AB=AC,∴∠BAF=∠CAF.
∵DE∥AC,∴∠EDA=∠CAF.
∴∠BAF=∠EDA.
∴AE=DE.
∵AE=EB+AB,AB=AC,
∴DE=BE+AC.
第2课时 三角形三边的垂直平分线
1.三角形纸片ABC上有一点P,量得PA=3 cm,PB=3 cm,则点P一定(D)
A.是边AB的中点 B.在边AB的中线上
C.在边AB的高上 D.在边AB的垂直平分线上
2.在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形(C)
A.三条中线的交点
B.三条角平分线的交点
C.三条边的垂直平分线的交点
D.三条高的交点
3.如果三角形中两条边的垂直平分线的交点在第三条边上,那么这个三角形一定是(D)
A.锐角三角形 B.钝角三角形
C.等边三角形 D.直角三角形
4.如图,已知直线MN为△ABC的边BC的垂直平分线.若AB,AC两边的垂直平分线相交于点O,当顶点A的位置移动时,点O始终在(A)
A.直线MN上
B.直线MN的左侧
C.直线MN的右侧
D.直线MN的左侧或右侧
5.下列作图语句正确的是(D)
A.过点P作线段AB的垂直平分线
B.在线段AB的延长线上取一点C,使AB=AC
C.过直线a和直线b外一点P作直线MN,使MN∥a∥b
D.过点P作直线AB的垂线
6.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
第6题图 第7题图
7.如图,在Rt△ABC中,∠B=90°,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点M,N,连接MN,分别与AC,BC交于点D,E,连接AE,则:
(1)∠ADE=90°;
(2)AE=EC;(填“=”“>”或“<”)
(3)当AB=3,AC=5时,△ABE的周长等于7.
8.为了推进农村新型合作医疗制度改革,准备在某镇新建一个医疗点P,使P到该镇A村、B村、C村所属的村委会所在地的距离都相等(A,B,C不在同一直线上,地理位置如图),请你用尺规作图的方法确定点P的位置.要求:写出已知、求作,不写作法,保留作图痕迹.
解:已知:A,B,C三点不在同一直线上.
求作:作一点P,使PA=PB=PC.
如图所示,点P即为所求的点.
9.在平面内,到三点A,B,C距离相等的点(D)
A.只有一个 B.有两个
C.有三个或三个以上 D.有一个或没有
10.如图,在△ABC中,∠BAC=90°,AB>AC.按下列步骤作图:
①分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N;
②作直线MN,与边AB相交于点D,连接CD.
下列说法不一定正确的是(C)
A.∠BDN=∠CDN B.∠ADC=2∠B
C.∠ACD=∠DCB D.2∠B+∠ACD=90°
11.等腰三角形的底角为40°,两腰的垂直平分线交于点P,则(B)
A.点P在三角形内
B.点P在三角形外
C.点P在三角形底边上
D.点P的位置与三角形的边长有关
12.如图,由于水资源缺乏,B,C两地不得不从黄河上的扬水站A引水,这就需要A,B,C之间铺设地下输水管道,有人设计了三种铺设方案:如图①②③,图中实线表示管道铺设线路,在图②中,AD垂直BC于点D;在图③中,OA=OB=OC.为减少渗漏,节约水资源,并降低工程造价,铺设线路应尽量缩短,已知△ABC恰好是一个边长为a的等边三角形,那么通过计算,你认为最好的铺设方案是方案③.
13.如图所示,已知线段a,b,求作等腰三角形,使高为a,腰长为b(a<b,尺规作图,保留作图痕迹).
解:作法:(1)作线段AD=a;
(2)过点D作直线MN⊥AD于点D;
(3)以点A为圆心,b为半径画弧,交MN于B,C两点,连接AB,AC,△ABC即为所求,如图所示.
14.如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=120°,求∠MCN的度数;
(2)若△CMN的周长为15 cm,求AB的长;
(3)若∠MFN=70°,求∠MCN的度数.
解:(1)∵DM,EN分别垂直平分AC和BC,
∴AM=CM,CN=BN.
∴∠A=∠ACM,∠B=∠BCN.
∴∠MCN=180°-(∠CMN+∠CNM)
=180°-(2∠A+2∠B)
=180°-2(180°-∠ACB)
=60°.
(2)∵AM=CM,BN=CN,∴△CMN的周长为CM+MN+CN=AM+MN+BN=AB.
∵△CMN的周长为15 cm,∴AB=15 cm.
(3)∵∠MFN=70°,
∴∠MNF+∠NMF=180°-70°=110°.
∵∠AMD=∠NMF,∠BNE=∠MNF,
∴∠AMD+∠BNE=∠NMF+∠MNF=110°.
∴∠A+∠B=90°-∠AMD+90°-∠BNE=70°.
又∵∠A=∠ACM,∠B=∠BCN,
∴∠MCN=180°-2(∠A+∠B)=40°.
【变式】 如图,在△ABC中,∠BAC=80°,若MP和NQ分别垂直平分AB和AC.
(1)求∠PAQ的度数;
(2)若△APQ周长为12,BC长为8,求PQ的长.
解:(1)设∠PAQ=x,∠CAP=y,∠BAQ=z,
∵MP和NQ分别垂直平分AB和AC,
∴AP=PB,AQ=CQ.
∴∠B=∠BAP=x+z,∠C=∠CAQ=x+y.
∵∠BAC=80°,
∴∠B+∠C=100°,
即x+y+z=80°,x+z+x+y=100°.
∴x=20°.
∴∠PAQ=20°.
(2)∵△APQ周长为12,
∴AQ+PQ+AP=12.
∵AQ=CQ,AP=PB,
∴CQ+PQ+PB=12,即BC+2PQ=12.
∵BC=8,
∴PQ=2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
