北师大版数学八年级下册:1.1 等腰三角形 同步练习(word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册:1.1 等腰三角形 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 21:07:38 | ||
图片预览




文档简介
1 等腰三角形
第1课时 全等三角形和等腰三角形的性质
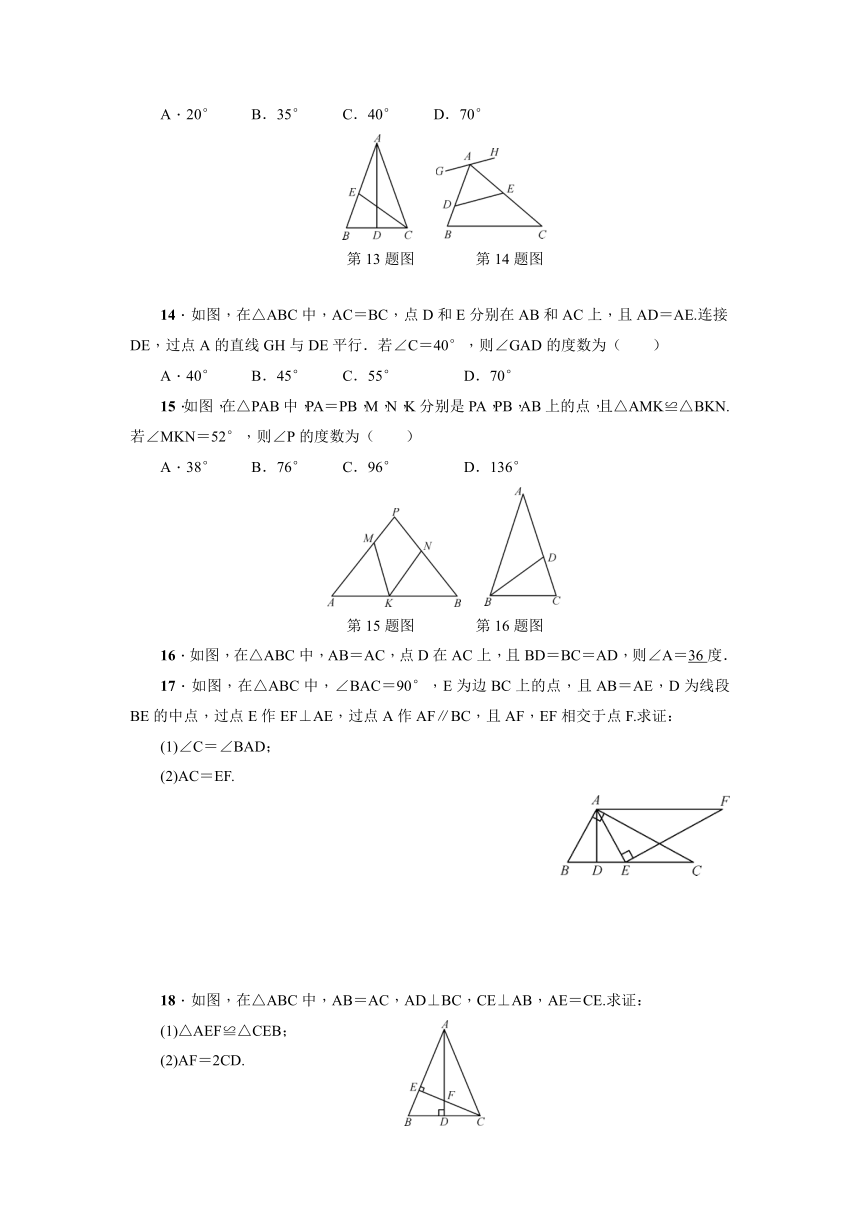
1.如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
第1题图 第2题图
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B= .
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 .
4.如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD= 度.
第4题图 第5题图
5.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE.若BC=15,DE=6,则CE的长为 .
6.已知:如图,在△ABC中,D是边AC上一点,AB=BD=DC,∠ABD=20°,AE∥BD交CB的延长线于点E.求∠AEB的度数.
7.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
第7题图 第8题图
8.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( )
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
9.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,CD=4,则△ABC的周长是 .
10.如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.
11.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17
C.13或17 D.13或10
12.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B等于 .
13.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
第13题图 第14题图
14.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行.若∠C=40°,则∠GAD的度数为( )
A.40° B.45° C.55° D.70°
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且△AMK≌△BKN.若∠MKN=52°,则∠P的度数为( )
A.38° B.76° C.96° D.136°
第15题图 第16题图
16.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=36度.
17.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)∠C=∠BAD;
(2)AC=EF.
18.如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
24123650(1)△AEF≌△CEB;
(2)AF=2CD.
第2课时 等腰三角形的特殊性质和等边三角形的性质
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE分别为AC,AB上的高
B.BD,CE为△ABC的角平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
第1题图 第2题图
2.如图,在△ABC中,AB=AC,BD,CE分别平分∠ABC和∠ACB,则下列结论不一定正确的是( )
A.BD=CE B.AE=AD
C.OC=DC D.∠ABD=∠ACE
3.求证:等腰三角形两腰上的高相等.
4.如图,在等边△ABC中,AD⊥BC于点D.若BD=2,则AC=( )
A.2 B.3 C.2 D.4
第4题图 第5题图
5.如图,在等边△ABC中,D是AC边的中点,延长BC到点E,使BD=DE,则∠CDE的度数为( )
A.15° B.20° C.30° D.40°
6.如图,△ABC为等边三角形,AC∥BD,则∠CBD= .
第6题图 第7题图
7.等边△ABC的边长如图所示,则y= .
8.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1= .
9.如图,在等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=CD,求证:BE=AD.
10.如图,△ABC是等边三角形,AD为中线,AD=AE,点E在边AC上,求∠EDC的度数.
11.如图,一个等边三角形纸片剪去一个角后变成一个四边形,则图中∠1+∠2的度数为( )
A.180° B.220° C.240° D.300°
第11题图 第12题图
12.如图,等边△OAB的边长为2,则点B的坐标为( )
A.(1,1) B.(1,)
C.(,1) D.(,)
13.如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE,交BD于点P,连接CD,分别交BE,AE于点Q,M,连接BM,PQ,则∠AMD的度数为( )
A.45° B.60° C.75° D.90°
第13题图 第14题图
14.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 .
357314535115515.如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
16.如图,△ABC为等边三角形,点M是线段BC上任意一点,点N是线段CA上任意一点,且BM=CN,BN与AM相交于点Q.
(1)求证:AM=BN;
(2)求∠BQM的度数.
17.已知,如图所示,P为等边△ABC内的一点,它到三边AB,AC,BC的距离分别为h1,h2,h3,△ABC的高AM=h,则h与h1,h2,h3有何数量关系?写出你的猜想并加以证明.
第3课时 等腰三角形的判定与反证法
1.在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AD平分外角∠EAC,且AD∥BC,则△ABC一定是( )
22066250A.任意三角形
B.等边三角形
C.等腰三角形
D.直角三角形
3.下列条件中不能说明三角形是等腰三角形的是( )
A.有两个内角分别是70°,40°的三角形
B.有一个角为45°的直角三角形
C.一个外角是130°,与它不相邻的一个内角为50°的三角形
D.有两个内角分别是70°,50°的三角形
4.如图,AC,BD相交于点O,∠A=∠D.如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是( )
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
第4题图 第5题图
5.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E.若DE=5,AE=7,则AC的长为 .
6.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
7.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
8.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
9.如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
10.如图,已知每个小方格的边长都为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
21685250A.8个
B.7个
C.6个
D.5个
11.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
第11题图 第12题图
12.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为( )
A.5 B.6 C.7 D.8
用反证法证明“一个三角形中最多有一个角是直角或钝角”时,应假设
.
14.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能将这个三角形分成两个小等腰三角形的是 (填序号).
,①) ,②) ,③) ,④)
15.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,过点F作FG⊥BC于点G,并交AB于点E,求证:
(1)AD∥FG;
(2)△AEF是等腰三角形.
16.如图,在等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC= ,∠DEC= ;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.在△ABC中,若AB=AC,∠A=∠C,则△ABC是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定
2.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中等边三角形是( )
A.①②③ B.①②④
C.①③④ D.①②③④
3.如图,将两个完全相同的含有30°角的三角板拼接在一起,则拼接后的△ABD是等边三角形.
第3题图 第4题图
4.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
5.如图,在△ABC中,点D是AB上一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
6.如图,点D,E在线段BC上,BD=CE,∠B=∠C,∠ADB=120°,求证:△ADE为等边三角形.
7.如图,在Rt△ABC中,∠C=90°,AB=8,∠A=30°,则BC=( )
A.8 B.6 C.4 D.2
第7题图 第8题图
8.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )
A.2 B.3 C.4 D.5
9.如图,在一次暴风灾害中,一棵大树在离地面2米处折断,树的另一部分倒地后与地面成30°角,那么这棵树折断之前的高度是6米.
第9题图 第10题图
10.如图,这是某超市自动扶梯的示意图,大厅两层之间的距离h=6.5米,自动扶梯的倾角为30°.若自动扶梯运行速度v=0.5米/秒,则顾客乘自动扶梯上一层楼的时间为26秒.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,BC=8 cm,求AD的长.
12.如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处.已知CD=1,∠B=30°,则BD的长是( )
A.1 B.2
C. D.2
第12题图 第13题图
13.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A.平行 B.相交
C.垂直 D.平行、相交或垂直
14.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A.3 B.4 C.5 D.6
第14题图 第15题图
15.如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上.如果边AB与l1的交点D是AB的中点,那么∠1= .
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB,交CD于点E,交BC于点F.若AF=BF,求证:△CEF是等边三角形.
17.在四边形ABCD中,AB=BC=CD=DA,∠B=∠D=60°,连接AC.
(1)如图1,点E,F分别在边BC,CD上,且BE=CF.求证:
①△ABE≌△ACF;
②△AEF是等边三角形;
(2)若点E在BC的延长线上,则在直线CD上是否存在点F,使△AEF是等边三角形?请证明你的结论(图2备用).
参考答案:
第1课时 全等三角形和等腰三角形的性质
1.如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是(A)
A.SAS B.AAS C.SSS D.ASA
第1题图 第2题图
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为34°.
4.如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=40度.
第4题图 第5题图
5.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE.若BC=15,DE=6,则CE的长为4.5.
6.已知:如图,在△ABC中,D是边AC上一点,AB=BD=DC,∠ABD=20°,AE∥BD交CB的延长线于点E.求∠AEB的度数.
解:∵AB=BD,∠ABD=20°,∴∠ADB=80°.
∵BD=DC,∴∠CBD=40°.
∵AE∥BD,∴∠AEB=40°.
7.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于(B)
A.10 B.5 C.4 D.3
第7题图 第8题图
8.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是(C)
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
9.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,CD=4,则△ABC的周长是20.
10.如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.
解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°.
∵AD=AB,
∴∠BDA=×(180°-40°)=70°.
∴∠E=∠BDA-∠CAD=70°-40°=30°.
11.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为(B)
A.13 B.17
C.13或17 D.13或10
12.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B等于70°或20°.
13.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是(B)
A.20° B.35° C.40° D.70°
第13题图 第14题图
14.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行.若∠C=40°,则∠GAD的度数为(C)
A.40° B.45° C.55° D.70°
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且△AMK≌△BKN.若∠MKN=52°,则∠P的度数为(B)
A.38° B.76° C.96° D.136°
第15题图 第16题图
16.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=36度.
17.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)∠C=∠BAD;
(2)AC=EF.
证明:(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC.
∴∠C+∠DAC=90°.
∵∠BAC=90°,
∴∠BAD+∠DAC=90°.
∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB.
∵AB=AE,∴∠B=∠AEB.
∴∠B=∠FAE.
∵EF⊥AE,
∴∠AEF=90°=∠BAC.
在△ABC和△EAF中,
∴△ABC≌△EAF(ASA).
∴AC=EF.
18.如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
证明:(1)∵AD⊥BC,CE⊥AB,
∴∠AEF=∠CEB=∠ADC=90°.
∴∠AFE+∠EAF=∠CFD+∠ECB=90°.
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
∴△AEF≌△CEB(ASA).
(2)∵△AEF≌△CEB,
∴AF=BC.
在△ABC中,AB=AC,AD⊥BC,
∴CD=BD.∴BC=2CD.
∴AF=2CD.
第2课时 等腰三角形的特殊性质和等边三角形的性质
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是(D)
A.BD,CE分别为AC,AB上的高
B.BD,CE为△ABC的角平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
第1题图 第2题图
2.如图,在△ABC中,AB=AC,BD,CE分别平分∠ABC和∠ACB,则下列结论不一定正确的是(C)
A.BD=CE B.AE=AD
C.OC=DC D.∠ABD=∠ACE
3.求证:等腰三角形两腰上的高相等.
已知:如图,在△ABC中,AB=AC,CE⊥AB于点E,BD⊥AC于点D.
求证:CE=BD.
证明:∵CE⊥AB,BD⊥AC,
∴∠AEC=∠ADB=90°.
又∵AC=AB,∠A=∠A,
∴△ACE≌△ABD(AAS).
∴CE=BD.
4.如图,在等边△ABC中,AD⊥BC于点D.若BD=2,则AC=(D)
A.2 B.3 C.2 D.4
第4题图 第5题图
5.如图,在等边△ABC中,D是AC边的中点,延长BC到点E,使BD=DE,则∠CDE的度数为(C)
A.15° B.20° C.30° D.40°
6.如图,△ABC为等边三角形,AC∥BD,则∠CBD=120°.
第6题图 第7题图
7.等边△ABC的边长如图所示,则y=3.
8.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1=40°.
9.如图,在等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=CD,求证:BE=AD.
证明:∵△ABC是等边三角形,
∴AB=CA,∠BAC=∠ACB=60°.
∴∠EAB=∠DCA=120°.
在△EAB和△DCA中,
∴△EAB≌△DCA(SAS).
∴BE=AD.
10.如图,△ABC是等边三角形,AD为中线,AD=AE,点E在边AC上,求∠EDC的度数.
解:∵△ABC是等边三角形,AD为中线,
∴AD⊥BC,∠CAD=30°.
∵AD=AE,
∴∠ADE=∠AED=(180°-∠CAD)=75°.
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
11.如图,一个等边三角形纸片剪去一个角后变成一个四边形,则图中∠1+∠2的度数为(C)
A.180° B.220° C.240° D.300°
第11题图 第12题图
12.如图,等边△OAB的边长为2,则点B的坐标为(B)
A.(1,1) B.(1,)
C.(,1) D.(,)
13.如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE,交BD于点P,连接CD,分别交BE,AE于点Q,M,连接BM,PQ,则∠AMD的度数为(B)
A.45° B.60° C.75° D.90°
第13题图 第14题图
14.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为60°.
15.如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
解:∵△ABC是等边三角形,BF是△ABC的高,
∴∠ABO=∠ABC=30°,
AB=AC.
∵AE=AC,∴AB=AE.
∵AO为∠BAE的平分线,
∴∠BAO=∠EAO.
在△ABO和△AEO中,
∴△ABO≌△AEO(SAS).
∴∠E=∠ABO=30°.
16.如图,△ABC为等边三角形,点M是线段BC上任意一点,点N是线段CA上任意一点,且BM=CN,BN与AM相交于点Q.
(1)求证:AM=BN;
(2)求∠BQM的度数.
解:(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AB=BC.
在△AMB和△BNC中,
∴△AMB≌△BNC(SAS).
∴AM=BN.
(2)∵△AMB≌△BNC,
∴∠MAB=∠NBC.
∴∠BQM=∠MAB+∠ABQ
=∠NBC+∠ABQ
=∠ABC
=60°.
17.已知,如图所示,P为等边△ABC内的一点,它到三边AB,AC,BC的距离分别为h1,h2,h3,△ABC的高AM=h,则h与h1,h2,h3有何数量关系?写出你的猜想并加以证明.
解:猜想:h1+h2+h3=h.
证明:连接PA,PB,PC.
∵S△PAB=AB·h1,
S△PAC=AC·h2,
S△PBC=BC·h3,
S△ABC=BC·h,
S△PAB+S△PAC+S△PBC=S△ABC,
∴AB·h1+AC·h2+BC·h3=BC·h.
∵△ABC是等边三角形,
∴AB=AC=BC.
∴h1+h2+h3=h.
第3课时 等腰三角形的判定与反证法
1.在△ABC中,已知∠B=∠C,则(B)
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AD平分外角∠EAC,且AD∥BC,则△ABC一定是(C)
A.任意三角形
B.等边三角形
C.等腰三角形
D.直角三角形
3.下列条件中不能说明三角形是等腰三角形的是(D)
A.有两个内角分别是70°,40°的三角形
B.有一个角为45°的直角三角形
C.一个外角是130°,与它不相邻的一个内角为50°的三角形
D.有两个内角分别是70°,50°的三角形
4.如图,AC,BD相交于点O,∠A=∠D.如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是(C)
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
第4题图 第5题图
5.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E.若DE=5,AE=7,则AC的长为12.
6.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
证明:∵DE∥AC,
∴∠CAD=∠ADE.
∵AD平分∠BAC,
∴∠CAD=∠DAE.
∴∠DAE=∠ADE.
∵AD⊥BD,
∴∠DAE+∠B=90°,∠ADE+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE.
∴△BDE是等腰三角形.
7.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
∴∠AFB=∠DEC,即∠GFE=∠GEF.
∴GE=GF.
8.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设(A)
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
9.如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
证明:假设AB与EF不垂直,则∠AME≠90°.
∵AB∥CD,
∴∠AME=∠CNE.
∴∠CNE≠90°,与已知条件CD⊥EF相矛盾.
∴假设不成立.
∴AB⊥EF.
10.如图,已知每个小方格的边长都为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有(A)
A.8个
B.7个
C.6个
D.5个
11.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是(D)
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
第11题图 第12题图
12.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为(A)
A.5 B.6 C.7 D.8
13.用反证法证明“一个三角形中最多有一个角是直角或钝角”时,应假设_这个三角形中至少有两个角是直角或钝角.
14.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能将这个三角形分成两个小等腰三角形的是②(填序号).
,①) ,②) ,③) ,④)
15.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,过点F作FG⊥BC于点G,并交AB于点E,求证:
(1)AD∥FG;
(2)△AEF是等腰三角形.
证明:(1)∵AB=AC,D是BC的中点,
∴AD⊥BC.∴∠ADC=90°.
∵FG⊥BC,∴∠FGC=90°.
∴∠ADC=∠FGC.
∴AD∥FG.
(2)∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE.
∴△AEF是等腰三角形.
16.如图,在等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF.
解:(1)∵BD是等边△ABC的中线,
∴BD⊥AC,AD=CD.
∵AB=6,∴AD=3.
在Rt△ABD中,由勾股定理,得
BD==3.
(2)证明:∵BD是等边△ABC的中线,
∴BD平分∠ABC.
∴∠DBE=∠ABC=30°.
∵∠ACB=60°,∴∠ACE=120°.
又∵CE=CD,∴∠E=∠CDE==30°.
∴∠DBE=∠E.∴BD=ED.
又∵DF⊥BE,
∴BF=EF.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=25°,∠DEC=115°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
解:(2)当DC=2时,△ABD≌△DCE.
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠ADB+∠EDC=140°.
∴∠ADB=∠DEC.
又∵AB=DC=2,
∴△ABD≌△DCE(AAS).
(3)可以,∠BDA的度数为110°或80°.
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.在△ABC中,若AB=AC,∠A=∠C,则△ABC是(B)
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定
2.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中等边三角形是(D)
A.①②③ B.①②④
C.①③④ D.①②③④
3.如图,将两个完全相同的含有30°角的三角板拼接在一起,则拼接后的△ABD是等边三角形.
第3题图 第4题图
4.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC=48米.
5.如图,在△ABC中,点D是AB上一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
证明:∵DC=DB,∠B=30°,
∴∠DCB=∠B=30°.
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
6.如图,点D,E在线段BC上,BD=CE,∠B=∠C,∠ADB=120°,求证:△ADE为等边三角形.
证明:∵∠B=∠C,
∴AB=AC.
又∵BD=CE,
∴△ABD≌△ACE(SAS).
∴AD=AE.
∵∠ADB=120°,
∴∠ADE=60°.
∴△ADE为等边三角形.
7.如图,在Rt△ABC中,∠C=90°,AB=8,∠A=30°,则BC=(C)
A.8 B.6 C.4 D.2
第7题图 第8题图
8.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是(D)
A.2 B.3 C.4 D.5
9.如图,在一次暴风灾害中,一棵大树在离地面2米处折断,树的另一部分倒地后与地面成30°角,那么这棵树折断之前的高度是6米.
第9题图 第10题图
10.如图,这是某超市自动扶梯的示意图,大厅两层之间的距离h=6.5米,自动扶梯的倾角为30°.若自动扶梯运行速度v=0.5米/秒,则顾客乘自动扶梯上一层楼的时间为26秒.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,BC=8 cm,求AD的长.
解:∵∠ACB=90°,∠A=30°,BC=8 cm,
∴∠B=60°,AB=2BC=16 cm.
∵CD⊥AB,
∴∠BDC=90°.
∴∠DCB=30°.
∴DB=BC=4 cm.
∴AD=AB-DB=12 cm.
12.如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处.已知CD=1,∠B=30°,则BD的长是(B)
A.1 B.2
C. D.2
第12题图 第13题图
13.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是(A)
A.平行 B.相交
C.垂直 D.平行、相交或垂直
14.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=(C)
A.3 B.4 C.5 D.6
第14题图 第15题图
15.如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上.如果边AB与l1的交点D是AB的中点,那么∠1=120°.
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB,交CD于点E,交BC于点F.若AF=BF,求证:△CEF是等边三角形.
证明:∵AF平分∠CAB,
∴∠CAF=∠BAF.
∵AF=BF,
∴∠BAF=∠B.
∴∠CAF=∠BAF=∠B.
∵∠ACB=90°,
∴∠CAF+∠BAF+∠B=90°.
∴∠BAF=∠B=30°.
∵CD⊥AB,∴∠ADE=∠CDB=90°.
∴∠BCD=∠DEA=60°.∴∠CEF=60°.
∴∠CFA=∠CEF=∠ECF=60°.
∴△CEF是等边三角形.
17.在四边形ABCD中,AB=BC=CD=DA,∠B=∠D=60°,连接AC.
(1)如图1,点E,F分别在边BC,CD上,且BE=CF.求证:
①△ABE≌△ACF;
②△AEF是等边三角形;
(2)若点E在BC的延长线上,则在直线CD上是否存在点F,使△AEF是等边三角形?请证明你的结论(图2备用).
解:(1)证明:①∵AB=BC,∠B=60°,
∴△ABC是等边三角形.∴AB=AC.
同理,△ADC也是等边三角形,
∴∠B=∠ACF=60°.
又∵BE=CF,∴△ABE≌△ACF(SAS).
②∵△ABE≌△ACF,
∴AE=AF,∠BAE=∠CAF.
∵∠BAE+∠CAE=60°,
∴∠CAF+∠CAE=60°,即∠EAF=60°.
∴△AEF是等边三角形.
(2)存在.
证明:在CD的延长线上取点F,在BC的延长线上取点E,使CF=BE,连接AE,EF,AF.
与(1)①同理,可证△ABE≌△ACF,
∴AE=AF,∠BAE=∠CAF.
∴∠BAE-∠CAE=∠CAF-∠CAE,
即∠BAC=∠EAF=60°.
∴△AEF是等边三角形.
第1课时 全等三角形和等腰三角形的性质
1.如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
第1题图 第2题图
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B= .
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为 .
4.如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD= 度.
第4题图 第5题图
5.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE.若BC=15,DE=6,则CE的长为 .
6.已知:如图,在△ABC中,D是边AC上一点,AB=BD=DC,∠ABD=20°,AE∥BD交CB的延长线于点E.求∠AEB的度数.
7.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于( )
A.10 B.5 C.4 D.3
第7题图 第8题图
8.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是( )
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
9.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,CD=4,则△ABC的周长是 .
10.如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.
11.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为( )
A.13 B.17
C.13或17 D.13或10
12.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B等于 .
13.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是( )
A.20° B.35° C.40° D.70°
第13题图 第14题图
14.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行.若∠C=40°,则∠GAD的度数为( )
A.40° B.45° C.55° D.70°
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且△AMK≌△BKN.若∠MKN=52°,则∠P的度数为( )
A.38° B.76° C.96° D.136°
第15题图 第16题图
16.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=36度.
17.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)∠C=∠BAD;
(2)AC=EF.
18.如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
24123650(1)△AEF≌△CEB;
(2)AF=2CD.
第2课时 等腰三角形的特殊性质和等边三角形的性质
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是( )
A.BD,CE分别为AC,AB上的高
B.BD,CE为△ABC的角平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
第1题图 第2题图
2.如图,在△ABC中,AB=AC,BD,CE分别平分∠ABC和∠ACB,则下列结论不一定正确的是( )
A.BD=CE B.AE=AD
C.OC=DC D.∠ABD=∠ACE
3.求证:等腰三角形两腰上的高相等.
4.如图,在等边△ABC中,AD⊥BC于点D.若BD=2,则AC=( )
A.2 B.3 C.2 D.4
第4题图 第5题图
5.如图,在等边△ABC中,D是AC边的中点,延长BC到点E,使BD=DE,则∠CDE的度数为( )
A.15° B.20° C.30° D.40°
6.如图,△ABC为等边三角形,AC∥BD,则∠CBD= .
第6题图 第7题图
7.等边△ABC的边长如图所示,则y= .
8.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1= .
9.如图,在等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=CD,求证:BE=AD.
10.如图,△ABC是等边三角形,AD为中线,AD=AE,点E在边AC上,求∠EDC的度数.
11.如图,一个等边三角形纸片剪去一个角后变成一个四边形,则图中∠1+∠2的度数为( )
A.180° B.220° C.240° D.300°
第11题图 第12题图
12.如图,等边△OAB的边长为2,则点B的坐标为( )
A.(1,1) B.(1,)
C.(,1) D.(,)
13.如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE,交BD于点P,连接CD,分别交BE,AE于点Q,M,连接BM,PQ,则∠AMD的度数为( )
A.45° B.60° C.75° D.90°
第13题图 第14题图
14.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为 .
357314535115515.如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
16.如图,△ABC为等边三角形,点M是线段BC上任意一点,点N是线段CA上任意一点,且BM=CN,BN与AM相交于点Q.
(1)求证:AM=BN;
(2)求∠BQM的度数.
17.已知,如图所示,P为等边△ABC内的一点,它到三边AB,AC,BC的距离分别为h1,h2,h3,△ABC的高AM=h,则h与h1,h2,h3有何数量关系?写出你的猜想并加以证明.
第3课时 等腰三角形的判定与反证法
1.在△ABC中,已知∠B=∠C,则( )
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AD平分外角∠EAC,且AD∥BC,则△ABC一定是( )
22066250A.任意三角形
B.等边三角形
C.等腰三角形
D.直角三角形
3.下列条件中不能说明三角形是等腰三角形的是( )
A.有两个内角分别是70°,40°的三角形
B.有一个角为45°的直角三角形
C.一个外角是130°,与它不相邻的一个内角为50°的三角形
D.有两个内角分别是70°,50°的三角形
4.如图,AC,BD相交于点O,∠A=∠D.如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是( )
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
第4题图 第5题图
5.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E.若DE=5,AE=7,则AC的长为 .
6.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
7.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
8.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
9.如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
10.如图,已知每个小方格的边长都为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
21685250A.8个
B.7个
C.6个
D.5个
11.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
第11题图 第12题图
12.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为( )
A.5 B.6 C.7 D.8
用反证法证明“一个三角形中最多有一个角是直角或钝角”时,应假设
.
14.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能将这个三角形分成两个小等腰三角形的是 (填序号).
,①) ,②) ,③) ,④)
15.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,过点F作FG⊥BC于点G,并交AB于点E,求证:
(1)AD∥FG;
(2)△AEF是等腰三角形.
16.如图,在等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC= ,∠DEC= ;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.在△ABC中,若AB=AC,∠A=∠C,则△ABC是( )
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定
2.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中等边三角形是( )
A.①②③ B.①②④
C.①③④ D.①②③④
3.如图,将两个完全相同的含有30°角的三角板拼接在一起,则拼接后的△ABD是等边三角形.
第3题图 第4题图
4.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.
5.如图,在△ABC中,点D是AB上一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
6.如图,点D,E在线段BC上,BD=CE,∠B=∠C,∠ADB=120°,求证:△ADE为等边三角形.
7.如图,在Rt△ABC中,∠C=90°,AB=8,∠A=30°,则BC=( )
A.8 B.6 C.4 D.2
第7题图 第8题图
8.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是( )
A.2 B.3 C.4 D.5
9.如图,在一次暴风灾害中,一棵大树在离地面2米处折断,树的另一部分倒地后与地面成30°角,那么这棵树折断之前的高度是6米.
第9题图 第10题图
10.如图,这是某超市自动扶梯的示意图,大厅两层之间的距离h=6.5米,自动扶梯的倾角为30°.若自动扶梯运行速度v=0.5米/秒,则顾客乘自动扶梯上一层楼的时间为26秒.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,BC=8 cm,求AD的长.
12.如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处.已知CD=1,∠B=30°,则BD的长是( )
A.1 B.2
C. D.2
第12题图 第13题图
13.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )
A.平行 B.相交
C.垂直 D.平行、相交或垂直
14.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A.3 B.4 C.5 D.6
第14题图 第15题图
15.如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上.如果边AB与l1的交点D是AB的中点,那么∠1= .
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB,交CD于点E,交BC于点F.若AF=BF,求证:△CEF是等边三角形.
17.在四边形ABCD中,AB=BC=CD=DA,∠B=∠D=60°,连接AC.
(1)如图1,点E,F分别在边BC,CD上,且BE=CF.求证:
①△ABE≌△ACF;
②△AEF是等边三角形;
(2)若点E在BC的延长线上,则在直线CD上是否存在点F,使△AEF是等边三角形?请证明你的结论(图2备用).
参考答案:
第1课时 全等三角形和等腰三角形的性质
1.如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是(A)
A.SAS B.AAS C.SSS D.ASA
第1题图 第2题图
2.如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=120°.
3.如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为34°.
4.如图,在△ABC中,点D在边BC上,AB=AD=DC,∠C=35°,则∠BAD=40度.
第4题图 第5题图
5.如图,在△ABC中,AB=AC,点D,E在边BC上,∠BAD=∠CAE.若BC=15,DE=6,则CE的长为4.5.
6.已知:如图,在△ABC中,D是边AC上一点,AB=BD=DC,∠ABD=20°,AE∥BD交CB的延长线于点E.求∠AEB的度数.
解:∵AB=BD,∠ABD=20°,∴∠ADB=80°.
∵BD=DC,∴∠CBD=40°.
∵AE∥BD,∴∠AEB=40°.
7.如图,AD是等腰三角形ABC的顶角平分线,BD=5,则CD等于(B)
A.10 B.5 C.4 D.3
第7题图 第8题图
8.如图,为了让电线杆垂直于地面,工程人员的操作方法通常是:从电线杆DE上一点A往地面拉两条长度相等的固定绳AB与AC,当固定点B,C到杆脚E的距离相等,且B,E,C在同一直线上时,电线杆DE就垂直于BC.工程人员这种操作方法的依据是(C)
A.等边对等角
B.垂线段最短
C.等腰三角形“三线合一”
D.线段垂直平分线上的点到这条线段两端点的距离相等
9.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,CD=4,则△ABC的周长是20.
10.如图,已知在等腰三角形ABC中,AB=AC,∠BAC=80°,AD⊥BC,AD=AB,连接BD并延长,交AC的延长线于点E,求∠E的度数.
解:∵AB=AC,∠BAC=80°,AD⊥BC,
∴∠BAD=∠CAD=∠BAC=40°.
∵AD=AB,
∴∠BDA=×(180°-40°)=70°.
∴∠E=∠BDA-∠CAD=70°-40°=30°.
11.已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为(B)
A.13 B.17
C.13或17 D.13或10
12.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到的锐角为50°,则∠B等于70°或20°.
13.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是(B)
A.20° B.35° C.40° D.70°
第13题图 第14题图
14.如图,在△ABC中,AC=BC,点D和E分别在AB和AC上,且AD=AE.连接DE,过点A的直线GH与DE平行.若∠C=40°,则∠GAD的度数为(C)
A.40° B.45° C.55° D.70°
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且△AMK≌△BKN.若∠MKN=52°,则∠P的度数为(B)
A.38° B.76° C.96° D.136°
第15题图 第16题图
16.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A=36度.
17.如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)∠C=∠BAD;
(2)AC=EF.
证明:(1)∵AB=AE,D为线段BE的中点,
∴AD⊥BC.
∴∠C+∠DAC=90°.
∵∠BAC=90°,
∴∠BAD+∠DAC=90°.
∴∠C=∠BAD.
(2)∵AF∥BC,∴∠FAE=∠AEB.
∵AB=AE,∴∠B=∠AEB.
∴∠B=∠FAE.
∵EF⊥AE,
∴∠AEF=90°=∠BAC.
在△ABC和△EAF中,
∴△ABC≌△EAF(ASA).
∴AC=EF.
18.如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
证明:(1)∵AD⊥BC,CE⊥AB,
∴∠AEF=∠CEB=∠ADC=90°.
∴∠AFE+∠EAF=∠CFD+∠ECB=90°.
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
∴△AEF≌△CEB(ASA).
(2)∵△AEF≌△CEB,
∴AF=BC.
在△ABC中,AB=AC,AD⊥BC,
∴CD=BD.∴BC=2CD.
∴AF=2CD.
第2课时 等腰三角形的特殊性质和等边三角形的性质
1.如图,在△ABC中,AB=AC,下列条件中,不能使BD=CE的是(D)
A.BD,CE分别为AC,AB上的高
B.BD,CE为△ABC的角平分线
C.∠ABD=∠ABC,∠ACE=∠ACB
D.∠ABD=∠BCE
第1题图 第2题图
2.如图,在△ABC中,AB=AC,BD,CE分别平分∠ABC和∠ACB,则下列结论不一定正确的是(C)
A.BD=CE B.AE=AD
C.OC=DC D.∠ABD=∠ACE
3.求证:等腰三角形两腰上的高相等.
已知:如图,在△ABC中,AB=AC,CE⊥AB于点E,BD⊥AC于点D.
求证:CE=BD.
证明:∵CE⊥AB,BD⊥AC,
∴∠AEC=∠ADB=90°.
又∵AC=AB,∠A=∠A,
∴△ACE≌△ABD(AAS).
∴CE=BD.
4.如图,在等边△ABC中,AD⊥BC于点D.若BD=2,则AC=(D)
A.2 B.3 C.2 D.4
第4题图 第5题图
5.如图,在等边△ABC中,D是AC边的中点,延长BC到点E,使BD=DE,则∠CDE的度数为(C)
A.15° B.20° C.30° D.40°
6.如图,△ABC为等边三角形,AC∥BD,则∠CBD=120°.
第6题图 第7题图
7.等边△ABC的边长如图所示,则y=3.
8.如图,直线a∥b,△ABC的顶点C在直线b上,边AB与直线b相交于点D.若△BCD是等边三角形,∠A=20°,则∠1=40°.
9.如图,在等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=CD,求证:BE=AD.
证明:∵△ABC是等边三角形,
∴AB=CA,∠BAC=∠ACB=60°.
∴∠EAB=∠DCA=120°.
在△EAB和△DCA中,
∴△EAB≌△DCA(SAS).
∴BE=AD.
10.如图,△ABC是等边三角形,AD为中线,AD=AE,点E在边AC上,求∠EDC的度数.
解:∵△ABC是等边三角形,AD为中线,
∴AD⊥BC,∠CAD=30°.
∵AD=AE,
∴∠ADE=∠AED=(180°-∠CAD)=75°.
∴∠EDC=∠ADC-∠ADE=90°-75°=15°.
11.如图,一个等边三角形纸片剪去一个角后变成一个四边形,则图中∠1+∠2的度数为(C)
A.180° B.220° C.240° D.300°
第11题图 第12题图
12.如图,等边△OAB的边长为2,则点B的坐标为(B)
A.(1,1) B.(1,)
C.(,1) D.(,)
13.如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE,交BD于点P,连接CD,分别交BE,AE于点Q,M,连接BM,PQ,则∠AMD的度数为(B)
A.45° B.60° C.75° D.90°
第13题图 第14题图
14.三个等边三角形的摆放位置如图所示,若∠1+∠2=120°,则∠3的度数为60°.
15.如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
解:∵△ABC是等边三角形,BF是△ABC的高,
∴∠ABO=∠ABC=30°,
AB=AC.
∵AE=AC,∴AB=AE.
∵AO为∠BAE的平分线,
∴∠BAO=∠EAO.
在△ABO和△AEO中,
∴△ABO≌△AEO(SAS).
∴∠E=∠ABO=30°.
16.如图,△ABC为等边三角形,点M是线段BC上任意一点,点N是线段CA上任意一点,且BM=CN,BN与AM相交于点Q.
(1)求证:AM=BN;
(2)求∠BQM的度数.
解:(1)证明:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AB=BC.
在△AMB和△BNC中,
∴△AMB≌△BNC(SAS).
∴AM=BN.
(2)∵△AMB≌△BNC,
∴∠MAB=∠NBC.
∴∠BQM=∠MAB+∠ABQ
=∠NBC+∠ABQ
=∠ABC
=60°.
17.已知,如图所示,P为等边△ABC内的一点,它到三边AB,AC,BC的距离分别为h1,h2,h3,△ABC的高AM=h,则h与h1,h2,h3有何数量关系?写出你的猜想并加以证明.
解:猜想:h1+h2+h3=h.
证明:连接PA,PB,PC.
∵S△PAB=AB·h1,
S△PAC=AC·h2,
S△PBC=BC·h3,
S△ABC=BC·h,
S△PAB+S△PAC+S△PBC=S△ABC,
∴AB·h1+AC·h2+BC·h3=BC·h.
∵△ABC是等边三角形,
∴AB=AC=BC.
∴h1+h2+h3=h.
第3课时 等腰三角形的判定与反证法
1.在△ABC中,已知∠B=∠C,则(B)
A.AB=BC B.AB=AC
C.BC=AC D.∠A=60°
2.如图,在△ABC中,AD平分外角∠EAC,且AD∥BC,则△ABC一定是(C)
A.任意三角形
B.等边三角形
C.等腰三角形
D.直角三角形
3.下列条件中不能说明三角形是等腰三角形的是(D)
A.有两个内角分别是70°,40°的三角形
B.有一个角为45°的直角三角形
C.一个外角是130°,与它不相邻的一个内角为50°的三角形
D.有两个内角分别是70°,50°的三角形
4.如图,AC,BD相交于点O,∠A=∠D.如果请你再补充一个条件,使得△BOC是等腰三角形,那么你补充的条件不能是(C)
A.OA=OD B.AB=CD
C.∠ABO=∠DCO D.∠ABC=∠DCB
第4题图 第5题图
5.如图,在△ABC中,CD平分∠ACB,DE∥BC交AC于点E.若DE=5,AE=7,则AC的长为12.
6.如图,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE是等腰三角形.
证明:∵DE∥AC,
∴∠CAD=∠ADE.
∵AD平分∠BAC,
∴∠CAD=∠DAE.
∴∠DAE=∠ADE.
∵AD⊥BD,
∴∠DAE+∠B=90°,∠ADE+∠BDE=90°.
∴∠B=∠BDE.
∴BE=DE.
∴△BDE是等腰三角形.
7.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
证明:∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE.
在△ABF和△DCE中,
∴△ABF≌△DCE(SAS).
∴∠AFB=∠DEC,即∠GFE=∠GEF.
∴GE=GF.
8.用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设(A)
A.直角三角形中两个锐角都大于45°
B.直角三角形中两个锐角都不大于45°
C.直角三角形中有一个锐角大于45°
D.直角三角形中有一个锐角不大于45°
9.如图,已知AB∥CD,CD⊥EF,垂足为N,AB与EF交于点M,求证:AB⊥EF.(用反证法证明)
证明:假设AB与EF不垂直,则∠AME≠90°.
∵AB∥CD,
∴∠AME=∠CNE.
∴∠CNE≠90°,与已知条件CD⊥EF相矛盾.
∴假设不成立.
∴AB⊥EF.
10.如图,已知每个小方格的边长都为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有(A)
A.8个
B.7个
C.6个
D.5个
11.如图,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是(D)
A.AE=AD B.BD=CE
C.∠ECB=∠DBC D.∠BEC=∠CDB
第11题图 第12题图
12.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交AB,AC于点D,E.若BD+CE=5,则线段DE的长为(A)
A.5 B.6 C.7 D.8
13.用反证法证明“一个三角形中最多有一个角是直角或钝角”时,应假设_这个三角形中至少有两个角是直角或钝角.
14.如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能将这个三角形分成两个小等腰三角形的是②(填序号).
,①) ,②) ,③) ,④)
15.如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上一点,过点F作FG⊥BC于点G,并交AB于点E,求证:
(1)AD∥FG;
(2)△AEF是等腰三角形.
证明:(1)∵AB=AC,D是BC的中点,
∴AD⊥BC.∴∠ADC=90°.
∵FG⊥BC,∴∠FGC=90°.
∴∠ADC=∠FGC.
∴AD∥FG.
(2)∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD.
∵AD∥FG,
∴∠F=∠CAD,∠AEF=∠BAD.
∴∠F=∠AEF.
∴AF=AE.
∴△AEF是等腰三角形.
16.如图,在等边△ABC中,AB=6,D是AC的中点,E是BC延长线上的一点,CE=CD,DF⊥BE,垂足为F.
(1)求BD的长;
(2)求证:BF=EF.
解:(1)∵BD是等边△ABC的中线,
∴BD⊥AC,AD=CD.
∵AB=6,∴AD=3.
在Rt△ABD中,由勾股定理,得
BD==3.
(2)证明:∵BD是等边△ABC的中线,
∴BD平分∠ABC.
∴∠DBE=∠ABC=30°.
∵∠ACB=60°,∴∠ACE=120°.
又∵CE=CD,∴∠E=∠CDE==30°.
∴∠DBE=∠E.∴BD=ED.
又∵DF⊥BE,
∴BF=EF.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=25°,∠DEC=115°;点D从B向C运动时,∠BDA逐渐变小(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE?请说明理由;
(3)在点D的运动过程中,△ADE可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
解:(2)当DC=2时,△ABD≌△DCE.
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠ADB+∠EDC=140°.
∴∠ADB=∠DEC.
又∵AB=DC=2,
∴△ABD≌△DCE(AAS).
(3)可以,∠BDA的度数为110°或80°.
第4课时 等边三角形的判定与含30°角的直角三角形的性质
1.在△ABC中,若AB=AC,∠A=∠C,则△ABC是(B)
A.等腰三角形 B.等边三角形
C.不等边三角形 D.不能确定
2.下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个角都相等的三角形;④三边都相等的三角形.其中等边三角形是(D)
A.①②③ B.①②④
C.①③④ D.①②③④
3.如图,将两个完全相同的含有30°角的三角板拼接在一起,则拼接后的△ABD是等边三角形.
第3题图 第4题图
4.如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC=48米.
5.如图,在△ABC中,点D是AB上一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
证明:∵DC=DB,∠B=30°,
∴∠DCB=∠B=30°.
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
6.如图,点D,E在线段BC上,BD=CE,∠B=∠C,∠ADB=120°,求证:△ADE为等边三角形.
证明:∵∠B=∠C,
∴AB=AC.
又∵BD=CE,
∴△ABD≌△ACE(SAS).
∴AD=AE.
∵∠ADB=120°,
∴∠ADE=60°.
∴△ADE为等边三角形.
7.如图,在Rt△ABC中,∠C=90°,AB=8,∠A=30°,则BC=(C)
A.8 B.6 C.4 D.2
第7题图 第8题图
8.如图,在△ABC中,∠C=90°,AC=2,∠B=30°,点P是BC边上一动点,连接AP,则AP的长度不可能是(D)
A.2 B.3 C.4 D.5
9.如图,在一次暴风灾害中,一棵大树在离地面2米处折断,树的另一部分倒地后与地面成30°角,那么这棵树折断之前的高度是6米.
第9题图 第10题图
10.如图,这是某超市自动扶梯的示意图,大厅两层之间的距离h=6.5米,自动扶梯的倾角为30°.若自动扶梯运行速度v=0.5米/秒,则顾客乘自动扶梯上一层楼的时间为26秒.
11.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,BC=8 cm,求AD的长.
解:∵∠ACB=90°,∠A=30°,BC=8 cm,
∴∠B=60°,AB=2BC=16 cm.
∵CD⊥AB,
∴∠BDC=90°.
∴∠DCB=30°.
∴DB=BC=4 cm.
∴AD=AB-DB=12 cm.
12.如图,折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处.已知CD=1,∠B=30°,则BD的长是(B)
A.1 B.2
C. D.2
第12题图 第13题图
13.如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是(A)
A.平行 B.相交
C.垂直 D.平行、相交或垂直
14.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=(C)
A.3 B.4 C.5 D.6
第14题图 第15题图
15.如图,已知直线l1∥l2,含30°角的三角板的直角顶点C在l1上,30°角的顶点A在l2上.如果边AB与l1的交点D是AB的中点,那么∠1=120°.
16.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AF平分∠CAB,交CD于点E,交BC于点F.若AF=BF,求证:△CEF是等边三角形.
证明:∵AF平分∠CAB,
∴∠CAF=∠BAF.
∵AF=BF,
∴∠BAF=∠B.
∴∠CAF=∠BAF=∠B.
∵∠ACB=90°,
∴∠CAF+∠BAF+∠B=90°.
∴∠BAF=∠B=30°.
∵CD⊥AB,∴∠ADE=∠CDB=90°.
∴∠BCD=∠DEA=60°.∴∠CEF=60°.
∴∠CFA=∠CEF=∠ECF=60°.
∴△CEF是等边三角形.
17.在四边形ABCD中,AB=BC=CD=DA,∠B=∠D=60°,连接AC.
(1)如图1,点E,F分别在边BC,CD上,且BE=CF.求证:
①△ABE≌△ACF;
②△AEF是等边三角形;
(2)若点E在BC的延长线上,则在直线CD上是否存在点F,使△AEF是等边三角形?请证明你的结论(图2备用).
解:(1)证明:①∵AB=BC,∠B=60°,
∴△ABC是等边三角形.∴AB=AC.
同理,△ADC也是等边三角形,
∴∠B=∠ACF=60°.
又∵BE=CF,∴△ABE≌△ACF(SAS).
②∵△ABE≌△ACF,
∴AE=AF,∠BAE=∠CAF.
∵∠BAE+∠CAE=60°,
∴∠CAF+∠CAE=60°,即∠EAF=60°.
∴△AEF是等边三角形.
(2)存在.
证明:在CD的延长线上取点F,在BC的延长线上取点E,使CF=BE,连接AE,EF,AF.
与(1)①同理,可证△ABE≌△ACF,
∴AE=AF,∠BAE=∠CAF.
∴∠BAE-∠CAE=∠CAF-∠CAE,
即∠BAC=∠EAF=60°.
∴△AEF是等边三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
