北师大版数学八年级下册:1.4 角平分线 同步练习(word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册:1.4 角平分线 同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 232.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 21:01:42 | ||
图片预览



文档简介
4 角平分线
第1课时 角平分线的性质定理及其逆定理
1.下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是( )
2.如图,点P是∠AOB的平分线上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD交OP于点E,下列结论不一定正确的是( )
A.PC=PD B.OC=OD
C.OP垂直平分CD D.OE=CD
第2题图 第3题图
3.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
4.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为 .
第4题图 第5题图
5.如图,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则△ABD的面积为 .
6.已知:如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,求证:OB=OC.
7.如图,DA⊥AC,DE⊥BC.若AD=5 cm,DE=5 cm,∠ACD=30°,则∠DCE=( )
23056850A.30°
B.40°
C.50°
D.60°
8.如图,BE=CF,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
9.已知D,E分别是△ABC中AB边,AC边上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB,理由如下:
因为点O到∠CAB两边的距离相等,所以点O在∠CAB的平分线上.所以AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
10.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
第10题图 第11题图
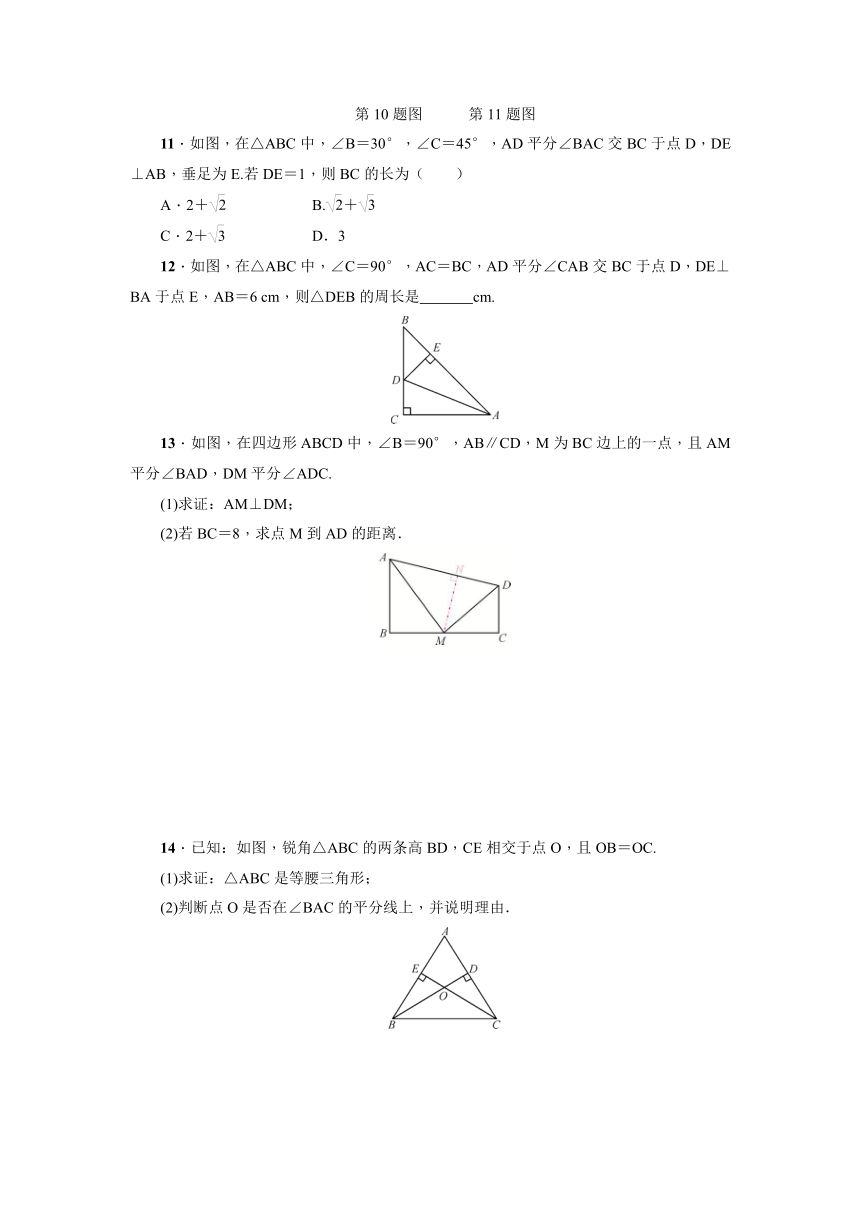
11.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )
A.2+ B.+
C.2+ D.3
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥BA于点E,AB=6 cm,则△DEB的周长是 cm.
13.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
14.已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
15.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=.若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
第2课时 三角形三个内角的平分线
1.到三角形三条边的距离相等的点是三角形________的交点( )
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1=2∠2
第2题图 第3题图
3.如图,在Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线相交于点O,OM⊥AB于点M.若OM=4,S△ABC=180,则△ABC的周长是 .
4.如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,求图中阴影部分的面积.
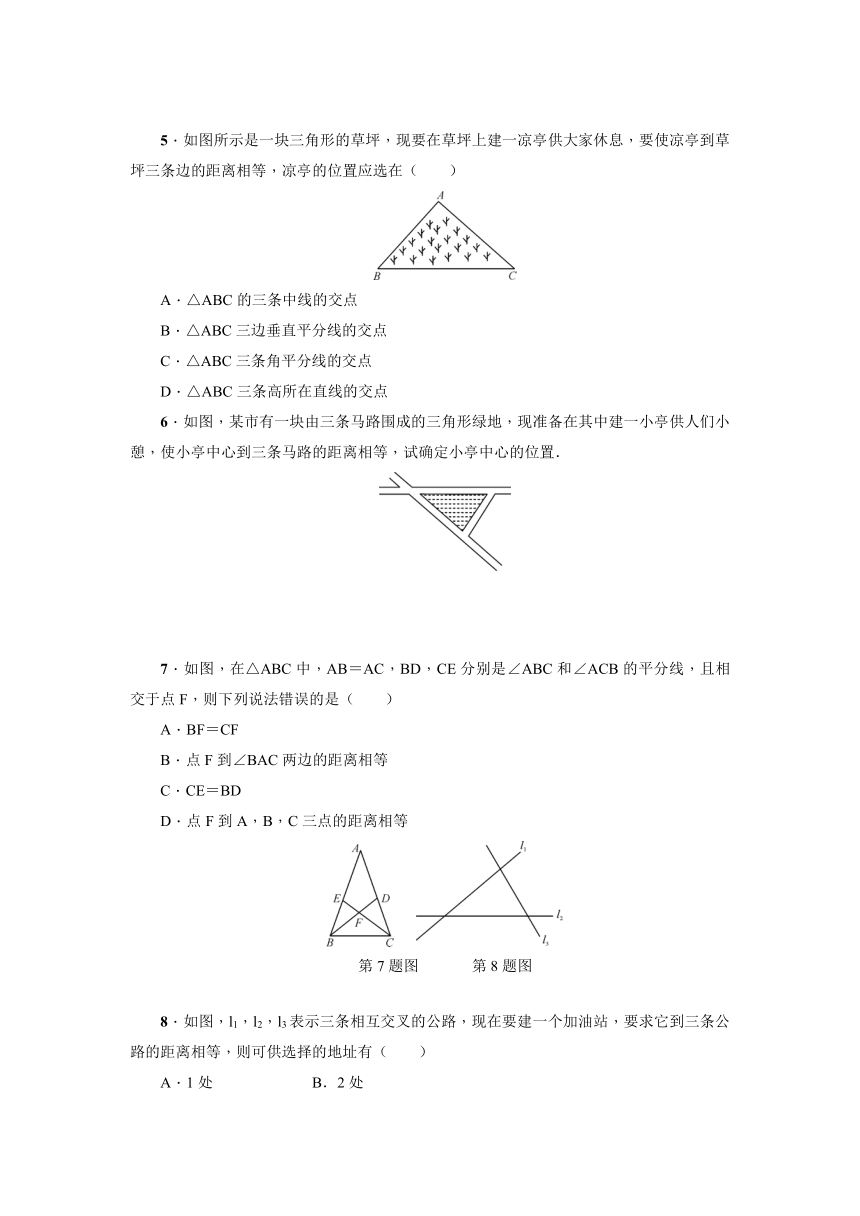
5.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
6.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
7.如图,在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的平分线,且相交于点F,则下列说法错误的是( )
A.BF=CF
B.点F到∠BAC两边的距离相等
C.CE=BD
D.点F到A,B,C三点的距离相等
第7题图 第8题图
8.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处
C.3处 D.4处
9.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,AE=7 cm,AP=4 cm,则点P到直线AB的距离是 .
10.如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+∠BAC.
11.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形(四边相等,四个角都是直角).
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
参考答案:
第1课时 角平分线的性质定理及其逆定理
1.下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是(D)
2.如图,点P是∠AOB的平分线上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD交OP于点E,下列结论不一定正确的是(D)
A.PC=PD B.OC=OD
C.OP垂直平分CD D.OE=CD
第2题图 第3题图
3.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于(C)
A.4 B.3 C.2 D.1
4.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为3.
第4题图 第5题图
5.如图,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则△ABD的面积为14.
6.已知:如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,求证:OB=OC.
证明:∵点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO和△CDO中,
∴△BEO≌△CDO(ASA).
∴OB=OC.
7.如图,DA⊥AC,DE⊥BC.若AD=5 cm,DE=5 cm,∠ACD=30°,则∠DCE=(A)
A.30°
B.40°
C.50°
D.60°
8.如图,BE=CF,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).
∴DE=DF.
∴AD是∠BAC的平分线.
9.已知D,E分别是△ABC中AB边,AC边上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB,理由如下:
因为点O到∠CAB两边的距离相等,所以点O在∠CAB的平分线上.所以AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
解:不正确.以上解法忽视了OD,OE分别垂直于AB,AC的条件,故产生错误.正确的结论是“AO不一定平分∠CAB”.
10.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是(A)
A.M点 B.N点 C.P点 D.Q点
第10题图 第11题图
11.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为(A)
A.2+ B.+
C.2+ D.3
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥BA于点E,AB=6 cm,则△DEB的周长是6cm.
13.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
解:(1)证明:∵AM平分∠BAD,DM平分∠ADC,
∴∠MAD=∠BAD,∠ADM=∠ADC.
∵AB∥CD,
∴∠BAD+∠ADC=180°.
∴∠MAD+∠ADM=(∠BAD+∠ADC)=90°.
又∵∠AMD+∠MAD+∠ADM=180°,
∴∠AMD=90°.
∴AM⊥DM.
(2)过点M作MN⊥AD于点N.
∵AB∥CD,∠B=90°,
∴∠C=90°,即BM⊥AB,MC⊥DC.
又∵AM,DM分别平分∠BAD,∠ADC,
∴BM=MN,MN=MC.
∴MN=BC=4.
∴点M到AD的距离为4.
14.已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
解:(1)证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°.
又∵∠EOB=∠DOC,
∴∠ABD=∠ACE.
∵OB=OC,
∴∠OBC=∠OCB.
∴∠ABC=∠ACB.
∴AB=AC.
∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:∵∠BEO=∠CDO=90°,∠BOE=∠COD,OB=OC,
∴△BOE≌△COD(AAS).
∴OE=OD.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上.
15.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=.若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
第2课时 三角形三个内角的平分线
1.到三角形三条边的距离相等的点是三角形________的交点(A)
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是(B)
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1=2∠2
第2题图 第3题图
3.如图,在Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线相交于点O,OM⊥AB于点M.若OM=4,S△ABC=180,则△ABC的周长是90.
4.如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,求图中阴影部分的面积.
解:连接OA,过点O作OE⊥AB于点E,OF⊥AC于点F.
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3.
同理可得OF=OD=3.
∴S阴影=S△AOB+S△AOC=AB·OE+AC·OF=(AB+AC)·OE=×20×3=30.
5.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(C)
A.△ABC的三条中线的交点
B.△ABC三边垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
6.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
解:如图所示,分别作三角形绿地两个角的平分线交于点P,点P即为所求.
7.如图,在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的平分线,且相交于点F,则下列说法错误的是(D)
A.BF=CF
B.点F到∠BAC两边的距离相等
C.CE=BD
D.点F到A,B,C三点的距离相等
第7题图 第8题图
8.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有(D)
A.1处 B.2处
C.3处 D.4处
9.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,AE=7 cm,AP=4 cm,则点P到直线AB的距离是3_cm.
10.如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+∠BAC.
证明:∵PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,
∴点P是△ABC三个内角平分线的交点.
∴CP平分∠ACB,BP平分∠ABC.
∴∠PCB=∠ACB,∠PBC=∠ABC.
∴∠BPC=180°-∠PCB-∠PBC
=180°-∠ACB-∠ABC
=180°-(∠ACB+∠ABC)
=180°-(180°-∠BAC)
=90°+∠BAC.
11.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形(四边相等,四个角都是直角).
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
解:(1)证明:过点O作OM⊥AB于点M.
∵BD是△ABC的一条角平分线,OM⊥AB,OE⊥BC,
∴OE=OM.
∵四边形OECF是正方形,
∴OE=OF,OF⊥AC.∴OM=OF.
∴点O在∠BAC的平分线上.
(2)∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴由勾股定理,得AB=13.
易证BE=BM,AM=AF.
∵BE=BC-CE,AF=AC-CF,CE=CF=OE,
∴BE=12-OE,AF=5-OE.
∵BM+AM=AB,
∴BE+AF=13,即12-OE+5-OE=13.
解得OE=2,即OE的长为2.
第1课时 角平分线的性质定理及其逆定理
1.下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是( )
2.如图,点P是∠AOB的平分线上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD交OP于点E,下列结论不一定正确的是( )
A.PC=PD B.OC=OD
C.OP垂直平分CD D.OE=CD
第2题图 第3题图
3.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于( )
A.4 B.3 C.2 D.1
4.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为 .
第4题图 第5题图
5.如图,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则△ABD的面积为 .
6.已知:如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,求证:OB=OC.
7.如图,DA⊥AC,DE⊥BC.若AD=5 cm,DE=5 cm,∠ACD=30°,则∠DCE=( )
23056850A.30°
B.40°
C.50°
D.60°
8.如图,BE=CF,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
9.已知D,E分别是△ABC中AB边,AC边上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB,理由如下:
因为点O到∠CAB两边的距离相等,所以点O在∠CAB的平分线上.所以AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
10.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是( )
A.M点 B.N点 C.P点 D.Q点
第10题图 第11题图
11.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为( )
A.2+ B.+
C.2+ D.3
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥BA于点E,AB=6 cm,则△DEB的周长是 cm.
13.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
14.已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
15.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=.若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
第2课时 三角形三个内角的平分线
1.到三角形三条边的距离相等的点是三角形________的交点( )
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是( )
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1=2∠2
第2题图 第3题图
3.如图,在Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线相交于点O,OM⊥AB于点M.若OM=4,S△ABC=180,则△ABC的周长是 .
4.如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,求图中阴影部分的面积.
5.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点
B.△ABC三边垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
6.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
7.如图,在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的平分线,且相交于点F,则下列说法错误的是( )
A.BF=CF
B.点F到∠BAC两边的距离相等
C.CE=BD
D.点F到A,B,C三点的距离相等
第7题图 第8题图
8.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处
C.3处 D.4处
9.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,AE=7 cm,AP=4 cm,则点P到直线AB的距离是 .
10.如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+∠BAC.
11.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形(四边相等,四个角都是直角).
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
参考答案:
第1课时 角平分线的性质定理及其逆定理
1.下列各图中,OP是∠MON的平分线,点E,F,G分别在射线OM,ON,OP上,则可以解释定理“角平分线上的点到角的两边的距离相等”的图形是(D)
2.如图,点P是∠AOB的平分线上一点,PC⊥OA于点C,PD⊥OB于点D,连接CD交OP于点E,下列结论不一定正确的是(D)
A.PC=PD B.OC=OD
C.OP垂直平分CD D.OE=CD
第2题图 第3题图
3.如图,在△ABC中,∠C=90°,AC=8,DC=AD,BD平分∠ABC,则点D到AB的距离等于(C)
A.4 B.3 C.2 D.1
4.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为3.
第4题图 第5题图
5.如图,BD平分∠ABC,DE⊥BC于点E,AB=7,DE=4,则△ABD的面积为14.
6.已知:如图所示,点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,垂足分别为D,E,DO,EO的延长线分别交AE,AD的延长线于点B,C,求证:OB=OC.
证明:∵点O在∠BAC的平分线上,OD⊥AC,OE⊥AB,
∴OE=OD,∠BEO=∠CDO=90°.
在△BEO和△CDO中,
∴△BEO≌△CDO(ASA).
∴OB=OC.
7.如图,DA⊥AC,DE⊥BC.若AD=5 cm,DE=5 cm,∠ACD=30°,则∠DCE=(A)
A.30°
B.40°
C.50°
D.60°
8.如图,BE=CF,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,且DB=DC,求证:AD是∠BAC的平分线.
证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠DFC=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).
∴DE=DF.
∴AD是∠BAC的平分线.
9.已知D,E分别是△ABC中AB边,AC边上的一点,在△ABC内有一点O,使OE=OD,则AO平分∠CAB吗?
解:AO平分∠CAB,理由如下:
因为点O到∠CAB两边的距离相等,所以点O在∠CAB的平分线上.所以AO平分∠CAB.
以上解法是否正确?若不正确,请说明理由,并写出正确的结论.
解:不正确.以上解法忽视了OD,OE分别垂直于AB,AC的条件,故产生错误.正确的结论是“AO不一定平分∠CAB”.
10.在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是(A)
A.M点 B.N点 C.P点 D.Q点
第10题图 第11题图
11.如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若DE=1,则BC的长为(A)
A.2+ B.+
C.2+ D.3
12.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥BA于点E,AB=6 cm,则△DEB的周长是6cm.
13.如图,在四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.
(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
解:(1)证明:∵AM平分∠BAD,DM平分∠ADC,
∴∠MAD=∠BAD,∠ADM=∠ADC.
∵AB∥CD,
∴∠BAD+∠ADC=180°.
∴∠MAD+∠ADM=(∠BAD+∠ADC)=90°.
又∵∠AMD+∠MAD+∠ADM=180°,
∴∠AMD=90°.
∴AM⊥DM.
(2)过点M作MN⊥AD于点N.
∵AB∥CD,∠B=90°,
∴∠C=90°,即BM⊥AB,MC⊥DC.
又∵AM,DM分别平分∠BAD,∠ADC,
∴BM=MN,MN=MC.
∴MN=BC=4.
∴点M到AD的距离为4.
14.已知:如图,锐角△ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
解:(1)证明:∵BD,CE是△ABC的高,
∴∠BEC=∠CDB=90°.
又∵∠EOB=∠DOC,
∴∠ABD=∠ACE.
∵OB=OC,
∴∠OBC=∠OCB.
∴∠ABC=∠ACB.
∴AB=AC.
∴△ABC是等腰三角形.
(2)点O在∠BAC的平分线上.
理由:∵∠BEO=∠CDO=90°,∠BOE=∠COD,OB=OC,
∴△BOE≌△COD(AAS).
∴OE=OD.
又∵OD⊥AC,OE⊥AB,
∴点O在∠BAC的平分线上.
15.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,AC=.若点P是AD上一动点,且作PN⊥AC于点N,则PN+PC的最小值是.
第2课时 三角形三个内角的平分线
1.到三角形三条边的距离相等的点是三角形________的交点(A)
A.三个内角平分线 B.三边垂直平分线
C.三条中线 D.三条高线
2.如图,在△ABC中,∠ABC,∠ACB的平分线相交于点O,下面结论中正确的是(B)
A.∠1>∠2 B.∠1=∠2
C.∠1<∠2 D.∠1=2∠2
第2题图 第3题图
3.如图,在Rt△ABC中,∠ACB=90°,△ABC的三条内角平分线相交于点O,OM⊥AB于点M.若OM=4,S△ABC=180,则△ABC的周长是90.
4.如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,求图中阴影部分的面积.
解:连接OA,过点O作OE⊥AB于点E,OF⊥AC于点F.
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3.
同理可得OF=OD=3.
∴S阴影=S△AOB+S△AOC=AB·OE+AC·OF=(AB+AC)·OE=×20×3=30.
5.如图所示是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在(C)
A.△ABC的三条中线的交点
B.△ABC三边垂直平分线的交点
C.△ABC三条角平分线的交点
D.△ABC三条高所在直线的交点
6.如图,某市有一块由三条马路围成的三角形绿地,现准备在其中建一小亭供人们小憩,使小亭中心到三条马路的距离相等,试确定小亭中心的位置.
解:如图所示,分别作三角形绿地两个角的平分线交于点P,点P即为所求.
7.如图,在△ABC中,AB=AC,BD,CE分别是∠ABC和∠ACB的平分线,且相交于点F,则下列说法错误的是(D)
A.BF=CF
B.点F到∠BAC两边的距离相等
C.CE=BD
D.点F到A,B,C三点的距离相等
第7题图 第8题图
8.如图,l1,l2,l3表示三条相互交叉的公路,现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有(D)
A.1处 B.2处
C.3处 D.4处
9.如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于点P,AE=7 cm,AP=4 cm,则点P到直线AB的距离是3_cm.
10.如图,在△ABC中,PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,求证:∠BPC=90°+∠BAC.
证明:∵PD⊥AC,PE⊥AB,PF⊥BC,PD=PE=PF,
∴点P是△ABC三个内角平分线的交点.
∴CP平分∠ACB,BP平分∠ABC.
∴∠PCB=∠ACB,∠PBC=∠ABC.
∴∠BPC=180°-∠PCB-∠PBC
=180°-∠ACB-∠ABC
=180°-(∠ACB+∠ABC)
=180°-(180°-∠BAC)
=90°+∠BAC.
11.如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形(四边相等,四个角都是直角).
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
解:(1)证明:过点O作OM⊥AB于点M.
∵BD是△ABC的一条角平分线,OM⊥AB,OE⊥BC,
∴OE=OM.
∵四边形OECF是正方形,
∴OE=OF,OF⊥AC.∴OM=OF.
∴点O在∠BAC的平分线上.
(2)∵在Rt△ABC中,∠C=90°,AC=5,BC=12,
∴由勾股定理,得AB=13.
易证BE=BM,AM=AF.
∵BE=BC-CE,AF=AC-CF,CE=CF=OE,
∴BE=12-OE,AF=5-OE.
∵BM+AM=AB,
∴BE+AF=13,即12-OE+5-OE=13.
解得OE=2,即OE的长为2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
