北师大版数学八年级下册:第三章 图形的平移与旋转 章末练习(word版含答案)
文档属性
| 名称 | 北师大版数学八年级下册:第三章 图形的平移与旋转 章末练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 267.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 20:36:14 | ||
图片预览



文档简介
图形的平移与旋转 章末练习
知识点1 平移
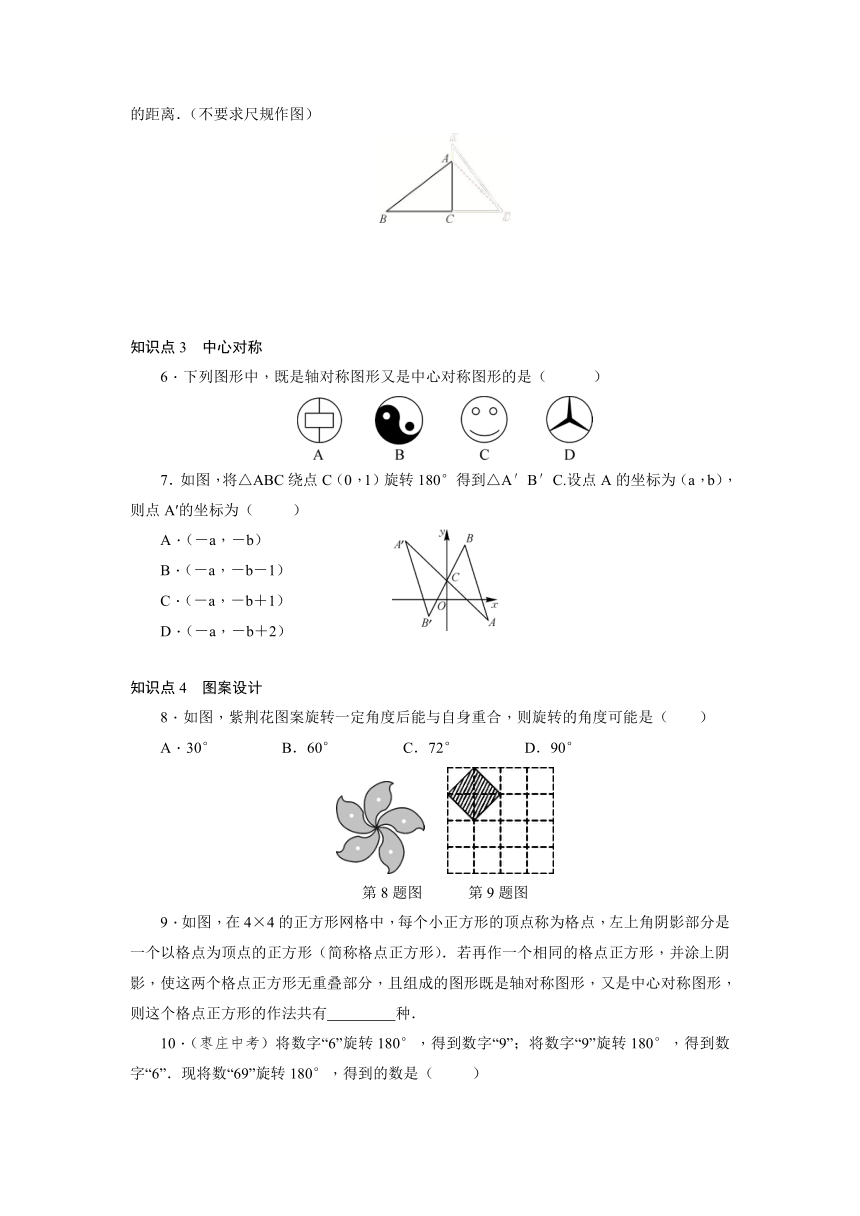
1.下列图形中,可由左图经过平移得到的是( )
A B C D
2.(2020·自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(-1,1) B.(5,1)
C.(2,4) D.(2,-2)
3.如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A,B,C的坐标;
(2)求出△AOA1的面积.
知识点2 旋转
4.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
5.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°.若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
知识点3 中心对称
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
7.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为( )
23056850A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
知识点4 图案设计
8.如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.72° D.90°
第8题图 第9题图
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个相同的格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 种.
10.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数“69”旋转180°,得到的数是( )
A.96 B.69 C.66 D.99
11.【分类讨论思想】如图,在△ABO中,AB⊥OB,OB=,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为 .
12.(2020·枣庄)如图的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A B C D
13.(2020·德阳)如图,在Rt△ABC中,∠A=30°,∠ABC=90°.将Rt△ABC绕点B逆时针方向旋转得到△A′BC′.此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为( )
A. B. C. D.
第13题图 第14题图
14.(2020·泰安)如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为 .
15.(2020·金昌)如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为 .
第15题图 第16题图
16.(2019·新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为 .
17.(2020·桂林)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点 中心对称.
18.窗棂即窗格(窗里面横的或竖的格)是中国传统木构建筑的框架结构设计.如图是我国古代窗棂样式结构的几种图案,其中既是中心对称图形又是轴对称图形的是( )
A B C D
参考答案:
知识点1 平移
1.下列图形中,可由左图经过平移得到的是(C)
A B C D
2.(2020·自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是(D)
A.(-1,1) B.(5,1)
C.(2,4) D.(2,-2)
3.如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A,B,C的坐标;
(2)求出△AOA1的面积.
解:(1)如图所示,A(-3,1),B(0,2),C(-1,4).
(2)S△AOA1=×4×1=2.
知识点2 旋转
4.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为15°.
5.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°.若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
解:如图.连接AD.
在Rt△ABC中,AB=5,BC=4,
∴AC==3.
由旋转的性质,得CD=AC=3,∠ACD=90°.
∴AD==3.
知识点3 中心对称
6.下列图形中,既是轴对称图形又是中心对称图形的是(A)
7.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为(D)
A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
知识点4 图案设计
8.如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是(C)
A.30° B.60° C.72° D.90°
第8题图 第9题图
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个相同的格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
10.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数“69”旋转180°,得到的数是(B)
A.96 B.69 C.66 D.99
11.【分类讨论思想】如图,在△ABO中,AB⊥OB,OB=,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为(-1,)或(1,-).
12.(2020·枣庄)如图的四个三角形中,不能由△ABC经过旋转或平移得到的是(B)
A B C D
13.(2020·德阳)如图,在Rt△ABC中,∠A=30°,∠ABC=90°.将Rt△ABC绕点B逆时针方向旋转得到△A′BC′.此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为(D)
A. B. C. D.
第13题图 第14题图
14.(2020·泰安)如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为(-2,1).
15.(2020·金昌)如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为(7,0).
第15题图 第16题图
16.(2019·新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为2-2.
17.(2020·桂林)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点(-2,0)中心对称.
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
18.窗棂即窗格(窗里面横的或竖的格)是中国传统木构建筑的框架结构设计.如图是我国古代窗棂样式结构的几种图案,其中既是中心对称图形又是轴对称图形的是(A)
A B C D
知识点1 平移
1.下列图形中,可由左图经过平移得到的是( )
A B C D
2.(2020·自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是( )
A.(-1,1) B.(5,1)
C.(2,4) D.(2,-2)
3.如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A,B,C的坐标;
(2)求出△AOA1的面积.
知识点2 旋转
4.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为 .
5.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°.若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
知识点3 中心对称
6.下列图形中,既是轴对称图形又是中心对称图形的是( )
7.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为( )
23056850A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
知识点4 图案设计
8.如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是( )
A.30° B.60° C.72° D.90°
第8题图 第9题图
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个相同的格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 种.
10.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数“69”旋转180°,得到的数是( )
A.96 B.69 C.66 D.99
11.【分类讨论思想】如图,在△ABO中,AB⊥OB,OB=,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为 .
12.(2020·枣庄)如图的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
A B C D
13.(2020·德阳)如图,在Rt△ABC中,∠A=30°,∠ABC=90°.将Rt△ABC绕点B逆时针方向旋转得到△A′BC′.此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为( )
A. B. C. D.
第13题图 第14题图
14.(2020·泰安)如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为 .
15.(2020·金昌)如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为 .
第15题图 第16题图
16.(2019·新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为 .
17.(2020·桂林)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点 中心对称.
18.窗棂即窗格(窗里面横的或竖的格)是中国传统木构建筑的框架结构设计.如图是我国古代窗棂样式结构的几种图案,其中既是中心对称图形又是轴对称图形的是( )
A B C D
参考答案:
知识点1 平移
1.下列图形中,可由左图经过平移得到的是(C)
A B C D
2.(2020·自贡)在平面直角坐标系中,将点(2,1)向下平移3个单位长度,所得点的坐标是(D)
A.(-1,1) B.(5,1)
C.(2,4) D.(2,-2)
3.如图,△A1B1C1是△ABC向右平移4个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
(1)请画出△ABC,并写出点A,B,C的坐标;
(2)求出△AOA1的面积.
解:(1)如图所示,A(-3,1),B(0,2),C(-1,4).
(2)S△AOA1=×4×1=2.
知识点2 旋转
4.如图,将△ABC绕点A逆时针旋转150°,得到△ADE,这时点B,C,D恰好在同一直线上,则∠B的度数为15°.
5.如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°.若点A,B的对应点分别是点D,E,画出旋转后的三角形,并求点A与点D之间的距离.(不要求尺规作图)
解:如图.连接AD.
在Rt△ABC中,AB=5,BC=4,
∴AC==3.
由旋转的性质,得CD=AC=3,∠ACD=90°.
∴AD==3.
知识点3 中心对称
6.下列图形中,既是轴对称图形又是中心对称图形的是(A)
7.如图,将△ABC绕点C(0,1)旋转180°得到△A′B′C.设点A的坐标为(a,b),则点A′的坐标为(D)
A.(-a,-b)
B.(-a,-b-1)
C.(-a,-b+1)
D.(-a,-b+2)
知识点4 图案设计
8.如图,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度可能是(C)
A.30° B.60° C.72° D.90°
第8题图 第9题图
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个相同的格点正方形,并涂上阴影,使这两个格点正方形无重叠部分,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.
10.(枣庄中考)将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数“69”旋转180°,得到的数是(B)
A.96 B.69 C.66 D.99
11.【分类讨论思想】如图,在△ABO中,AB⊥OB,OB=,AB=1.将△ABO绕O点旋转90°后得到△A1B1O,则点A1的坐标为(-1,)或(1,-).
12.(2020·枣庄)如图的四个三角形中,不能由△ABC经过旋转或平移得到的是(B)
A B C D
13.(2020·德阳)如图,在Rt△ABC中,∠A=30°,∠ABC=90°.将Rt△ABC绕点B逆时针方向旋转得到△A′BC′.此时恰好点C在A′C′上,A′B交AC于点E,则△ABE与△ABC的面积之比为(D)
A. B. C. D.
第13题图 第14题图
14.(2020·泰安)如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A,B,C的坐标分别为A(0,3),B(-1,1),C(3,1).△A′B′C′是△ABC关于x轴的对称图形,将△A′B′C′绕点B′逆时针旋转180°,点A′的对应点为M,则点M的坐标为(-2,1).
15.(2020·金昌)如图,在平面直角坐标系中,△OAB的顶点A,B的坐标分别为(3,),(4,0).把△OAB沿x轴向右平移得到△CDE,如果点D的坐标为(6,),则点E的坐标为(7,0).
第15题图 第16题图
16.(2019·新疆)如图,在△ABC中,AB=AC=4,将△ABC绕点A顺时针旋转30°,得到△ACD,延长AD交BC的延长线于点E,则DE的长为2-2.
17.(2020·桂林)如图,在平面直角坐标系中,△ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把△ABC向左平移4个单位后得到对应的△A1B1C1,请画出平移后的△A1B1C1;
(2)把△ABC绕原点O旋转180°后得到对应的△A2B2C2,请画出旋转后的△A2B2C2;
(3)观察图形可知,△A1B1C1与△A2B2C2关于点(-2,0)中心对称.
解:(1)如图所示,△A1B1C1即为所求.
(2)如图所示,△A2B2C2即为所求.
18.窗棂即窗格(窗里面横的或竖的格)是中国传统木构建筑的框架结构设计.如图是我国古代窗棂样式结构的几种图案,其中既是中心对称图形又是轴对称图形的是(A)
A B C D
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
