北师大版数学八年级下册:第一章 三角形的证明 专题练习(word含答案)
文档属性
| 名称 | 北师大版数学八年级下册:第一章 三角形的证明 专题练习(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 676.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 20:33:05 | ||
图片预览




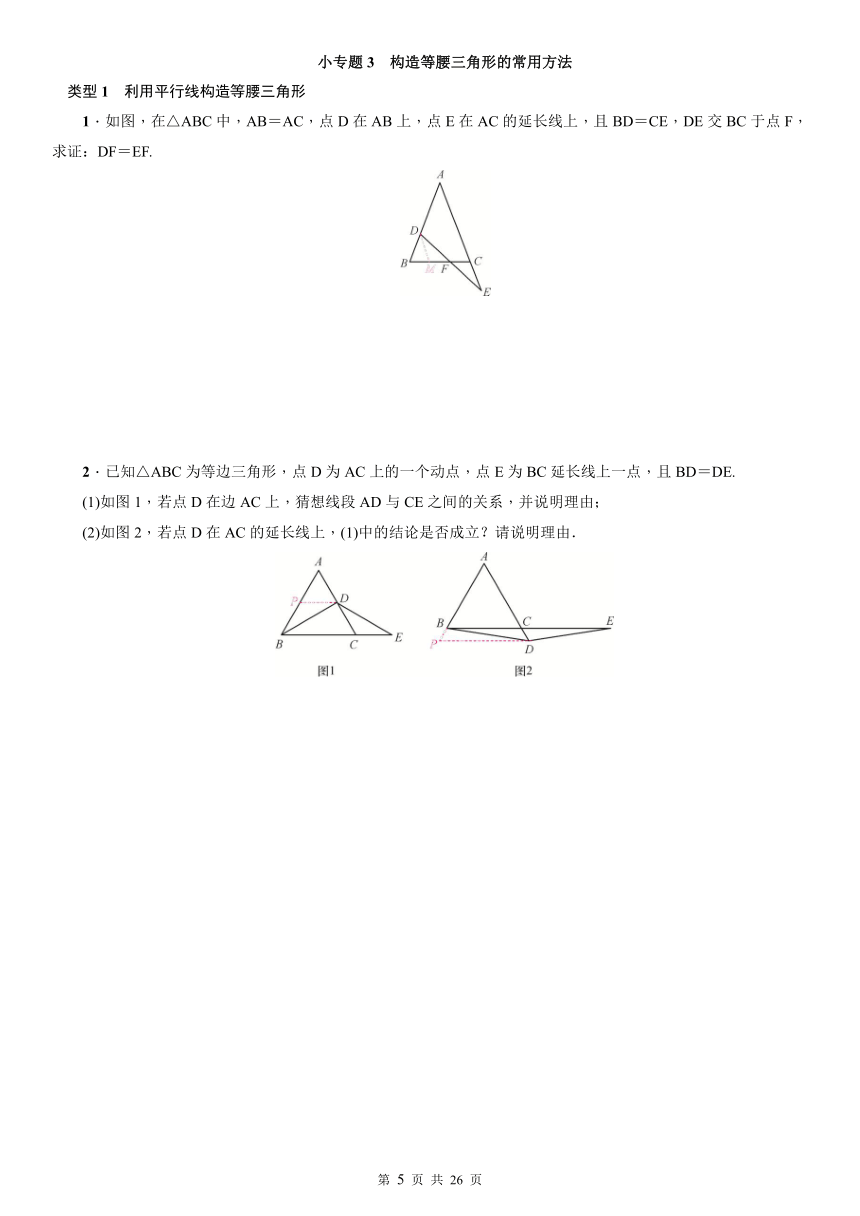
文档简介
小专题1 等腰三角形中的分类讨论思想
类型1 针对腰长和底边长进行分类
1.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .
2.若实数x,y满足|x-5|+=0,则以x,y的值为边长的等腰三角形的周长为 .
类型2 针对顶角和底角进行分类
3.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
4.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=80°,则它的特征值k= .
5.若等腰三角形中有一个角为52°,则它的一条腰上的高与底边的夹角的度数为 .
类型3 针对锐角、直角和钝角三角形进行分类
6.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为40°,则底角∠B等于( )
A.20° B.60°或20°
C.65°或25° D.60°
7.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其底边上的高是 .
8.已知等腰三角形一腰上的高与另一腰的夹角为36°,求这个等腰三角形的底角的度数.
类型4 确定等腰三角形的数目
9.如图,在平面直角坐标系中,已知A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5 B.6
C.7 D.8
第9题图 第10题图
10.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A.1个 B.2个
C.3个 D.3个以上
类型5 等腰三角形中的动点问题
11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10 cm,动点P从点A出发沿AB以2 cm/s的速度移动,动点Q从点O出发沿OC以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=或10时,△POQ是等腰三角形.
小专题2 特殊三角形中常用辅助线的作法
类型1 利用等腰三角形“三线合一”作辅助线
方法1 遇到等腰三角形常作底边上的高
1.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于点D,E是AD上一点,且EA=EC,求证:EB⊥AB.
方法2 当等腰三角形中有底边中点时,常连底边上的中线
2.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O为AB的中点,OE⊥OF分别交AC,BC于点E,F.求证:OE=OF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,求CE的长.
类型2 巧用特殊角构造含30°角的直角三角形
方法1 连接两点构造含30°角的直角三角形
4.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,DE=2,则BC的长为 .
方法2 延长两边构造含30°角的直角三角形(补形)
5.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,则CD= .
第5题图 第6题图
方法3 作垂线构造含30°角的直角三角形
6.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= .
7.如图,在△ABC中,BD是AC边上的中线,BD⊥BC于点B,∠ABD=30°,求证:AB=2BC.
小专题3 构造等腰三角形的常用方法
类型1 利用平行线构造等腰三角形
1.如图,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F,求证:DF=EF.
2.已知△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立?请说明理由.
类型2 运用倍角关系构造等腰三角形
3.如图,在△ABC中,AD平分∠BAC交BC于点D,且∠ABC=2∠C,求证:AB+BD=AC.
类型3 截长补短构造等腰三角形
4.如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数.(用截长法与补短法两种方法解答)
5.如图,在△ABC中,∠ABC=2∠ACB<90°,且AD⊥BC于点D.求证:AB+BD=CD.
小专题4 等腰直角三角形常见的解题模型
模型1 等腰直角三角形+斜边的中点→连接直角顶点和斜边中点
1.如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形.
【变式1】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别在AC,AB上,且DE⊥DF.试判断DE,DF的数量关系,并说明理由.
【变式2】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别为AB,CA延长线上的点,且BE=AF,那么△DEF是否仍为等腰直角三角形?证明你的结论.
模型2 等腰直角三角形+8字模型中有两直角,常用截长补短构造全等
2.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若CE⊥BD于点E,连接AE.求证:∠AEB=45°.
模型2变式 等腰直角三角形及8字模型中只有一个直角,过等腰直角三角形的顶点作垂线构造直角
3.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若∠AEB=45°.求证:CE⊥BD.
【变式】 将第3题中的“∠AEB=45°”改为“∠AEC=135°”,第3题中的结论还成立吗?并说明理由.
补充模型 三垂直模型
4.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
小专题5 角平分线的综合运用
模型1 双垂线型
1.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC;
(2)如图3,AD平分∠BAC,BD=DC,AC≠AB,求证:∠ABD+∠ACD=180°.
,图1) ,图2) ,图3)
【变式】 如图,∠CAB=40°,点D为∠CAB的平分线与线段BC的垂直平分线的交点,连接CD,试求∠DCB的度数.
模型2 截长补短型
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD.
【变式】 已知,在△ABC中,BD为∠ABC的平分线.
(1)如图1,若∠A=100°,∠C=50°,求证:BC=BA+AD;
(2)如图2,若∠BAC=100°,∠C=40°,求证:BC=BD+AD.
图1 图2
模型3 延长相交型
3.如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
模型4 平行等腰型
4.如图,在△ABC中,∠ABC=2∠ACB,AO,BO分别平分∠BAC,∠ABC,连接OC.
(1)求证:OC平分∠ACB;
(2)若AB=6,AC=10,求OB的长.
【变式】 如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC.若AN=1,则BC的长为 .
参考答案:
小专题1 等腰三角形中的分类讨论思想
类型1 针对腰长和底边长进行分类
1.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是10或11.
2.若实数x,y满足|x-5|+=0,则以x,y的值为边长的等腰三角形的周长为25.
类型2 针对顶角和底角进行分类
3.等腰三角形的一个内角为70°,则另外两个内角的度数分别是(D)
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
4.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=80°,则它的特征值k=或.
5.若等腰三角形中有一个角为52°,则它的一条腰上的高与底边的夹角的度数为26°或38°.
类型3 针对锐角、直角和钝角三角形进行分类
6.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为40°,则底角∠B等于(C)
A.20° B.60°或20°
C.65°或25° D.60°
7.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其底边上的高是3或3.
8.已知等腰三角形一腰上的高与另一腰的夹角为36°,求这个等腰三角形的底角的度数.
解:分两种情况讨论:
①若∠A<90°,如图1所示.
∵BD⊥AC,∴∠A+∠ABD=90°.
∵∠ABD=36°,∴∠A=90°-36°=54°.
∵AB=AC,
∴∠ABC=∠C=×(180°-54°)=63°.
②若∠A>90°,如图2所示.
同①可得∠DAB=90°-36°=54°,
∵AB=AC,
∴∠ABC=∠C=∠DAB=27°.
综上所述,等腰三角形底角的度数为63°或27°.
类型4 确定等腰三角形的数目
9.如图,在平面直角坐标系中,已知A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是(A)
A.5 B.6
C.7 D.8
第9题图 第10题图
10.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有(D)
A.1个 B.2个
C.3个 D.3个以上
类型5 等腰三角形中的动点问题
11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10 cm,动点P从点A出发沿AB以2 cm/s的速度移动,动点Q从点O出发沿OC以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=或10时,△POQ是等腰三角形.
小专题2 特殊三角形中常用辅助线的作法
类型1 利用等腰三角形“三线合一”作辅助线
方法1 遇到等腰三角形常作底边上的高
1.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于点D,E是AD上一点,且EA=EC,求证:EB⊥AB.
证明:过点E作EF⊥AC于点F.
∵EA=EC,
∴AF=FC=AC.
∵AC=2AB,∴AF=AB.
∵AD平分∠BAC,∴∠BAD=∠CAD.
在△ABE和△AFE中,
∴△ABE≌△AFE(SAS).
∴∠ABE=∠AFE=90°.∴EB⊥AB.
方法2 当等腰三角形中有底边中点时,常连底边上的中线
2.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O为AB的中点,OE⊥OF分别交AC,BC于点E,F.求证:OE=OF.
证明:连接OC.
∵AC=BC,∠ACB=90°,点O为AB的中点,
∴∠B=∠ACO=∠BCO=45°,CO⊥AB.
∴OC=OB,∠COB=90°.
又∵∠EOF=90°,∴∠EOC=∠FOB.
在△EOC和△FOB中,
∴△EOC≌△FOB(ASA).∴OE=OF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,求CE的长.
解:连接AD.
∵AB=AC,∠BAC=120°,D为BC的中点,
∴∠DAC=∠BAC=60°,∠ADC=90°.
∵DE⊥AC,∴∠ADE=90°-60°=30°.
∴AD=2AE=4.
又∵∠C=90°-∠DAC=30°,
∴AC=2AD=8.
∴CE=AC-AE=8-2=6.
类型2 巧用特殊角构造含30°角的直角三角形
方法1 连接两点构造含30°角的直角三角形
4.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,DE=2,则BC的长为12.
方法2 延长两边构造含30°角的直角三角形(补形)
5.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,则CD=2.
第5题图 第6题图
方法3 作垂线构造含30°角的直角三角形
6.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF=2.
7.如图,在△ABC中,BD是AC边上的中线,BD⊥BC于点B,∠ABD=30°,求证:AB=2BC.
证明:过点A作AM⊥BD,交BD的延长线于点M.
∵在Rt△ABM中,∠ABD=30°,
∴AB=2AM.
∵BD为AC边上的中线,∴AD=CD.
∵DB⊥BC,AM⊥BD,∴∠DBC=∠M=90°.
在△BCD和△MAD中,
∴△BCD≌△MAD(AAS).
∴BC=AM.
∴AB=2BC.
小专题3 构造等腰三角形的常用方法
类型1 利用平行线构造等腰三角形
1.如图,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F,求证:DF=EF.
证明:过点D作DM∥AC,交BC于点M.
∴∠DMB=∠ACB,∠FDM=∠E.
∵AB=AC,∴∠B=∠ACB.
∴∠B=∠DMB.∴BD=MD.
∵BD=CE,∴MD=CE.
在△DMF和△ECF中,
∴△DMF≌△ECF(AAS).
∴DF=EF.
2.已知△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立?请说明理由.
解:(1)AD=CE.
理由:过点D作DP∥BC,交AB于点P.
∵△ABC是等边三角形,
∴∠APD=∠ABC=∠ACB=∠PDA=60°.
∴△APD也是等边三角形.
∴AP=PD=AD.
∵DB=DE,∴∠DBC=∠DEC.
∵DP∥BC,∴∠PDB=∠CBD.
∴∠PDB=∠DEC.
∵∠BPD=180°-∠APD=120°,∠DCE=180°-∠ACB=120°,∴∠BPD=∠DCE.
在△BPD和△DCE中,
∴△BPD≌△DCE(AAS).
∴PD=CE.∴AD=CE.
(2)AD=CE成立.
理由:过点D作DP∥BC,交AB的延长线于点P.
∵△ABC是等边三角形,
∴∠APD=∠ABC=∠ACB=∠PDC=60°.
∴△APD也是等边三角形.
∴AP=PD=AD.
∵DB=DE,∴∠DBC=∠DEC.
∵DP∥BC,∴∠PDB=∠CBD.
∴∠PDB=∠DEC.
∵∠DCE=∠ACB=60°,
∴∠P=∠DCE.
在△BPD和△DCE中,
∴△BPD≌△DCE(AAS).∴PD=CE.
∴AD=CE.
类型2 运用倍角关系构造等腰三角形
3.如图,在△ABC中,AD平分∠BAC交BC于点D,且∠ABC=2∠C,求证:AB+BD=AC.
证明:方法1:在边AC上截取AP=AB,连接PD.
∵AD是∠BAC的平分线,
∴∠BAD=∠PAD.
在△ABD和△APD中,
∴△ABD≌△APD(SAS).
∴∠B=∠APD,BD=PD.
∵∠B=2∠C,∠APD=∠PDC+∠C,
∴∠PDC=∠C.
∴PD=PC.∴BD=PC.
∴AB+BD=AP+PC=AC.
方法2:延长AB至点E,使BE=BD,连接DE,证△AED≌△ACD即可.
方法3:延长CB至点E,使BE=AB,连接AE,则∠E=∠C=∠EAB,易证∠EAD=∠EDA,∴AC=EA=ED=EB+BD=AB+BD.
类型3 截长补短构造等腰三角形
4.如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数.(用截长法与补短法两种方法解答)
解:方法1(截长法):在CD上取点E,使DE=BD,连接AE,则△ADB≌△ADE(SAS),
∴CE=AB=AE.
∴∠B=∠AED=∠C+∠CAE=2∠C.
∵∠BAC=120°,∴∠B+∠C=2∠C+∠C=60°.∴∠C=20°.
方法2(补短法):延长DB至点F,使BF=AB,连接AF,则AB+BD=DF=CD.
∴△ADF≌△ADC(SAS).
∴AF=AC,∠C=∠F=∠ABC.
∵∠BAC=120°,
∴∠ABC+∠C=∠ABC+∠ABC=60°.
∴∠ABC=40°.
∴∠C=20°.
5.如图,在△ABC中,∠ABC=2∠ACB<90°,且AD⊥BC于点D.求证:AB+BD=CD.
证明:方法1(截长法):在CD上取点E,使DE=BD,连接AE,
易证△ABD≌△AED,则AB=AE,∠ABC=∠AED.
∵∠ABC=2∠ACB,
∴∠AED=∠ACB+∠CAE=2∠ACB.
∴∠CAE=∠ACB.
∴AE=EC.
∴AB+BD=EC+DE=CD.
方法2(补短法):延长DB至点F,使BF=AB,连接AF,
由BF=AB可知,∠F=∠FAB,
∴∠ABC=2∠F.
∵∠ABC=2∠ACB,
∴∠F=∠ACB.
易证△ADF≌△ADC,则AB+BD=DF=CD.
小专题4 等腰直角三角形常见的解题模型
模型1 等腰直角三角形+斜边的中点→连接直角顶点和斜边中点
1.如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形.
证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=BD=CD,∠BAD=∠CAD=∠B=45°,AD⊥BC.
在△BDE和△ADF中,
∴△BDE≌△ADF(SAS).
∴DE=DF,∠BDE=∠ADF.
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°.
∴△EDF为等腰直角三角形.
【变式1】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别在AC,AB上,且DE⊥DF.试判断DE,DF的数量关系,并说明理由.
解:DE=DF,理由如下:
连接AD,∵∠BAC=90°,AB=AC,D为BC中点,
∴CD=AD,∠C=∠DAF=45°,AD⊥BC.
∴∠CDE+∠EDA=∠ADF+∠EDA=90°.
∴∠CDE=∠ADF.
在△CDE和△ADF中,
∴△CDE≌△ADF(ASA).
∴DE=DF.
【变式2】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别为AB,CA延长线上的点,且BE=AF,那么△DEF是否仍为等腰直角三角形?证明你的结论.
解:△DEF仍为等腰直角三角形.
证明:连接AD,
∵AB=AC,
∴△ABC为等腰三角形.
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC.
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又∵AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
模型2 等腰直角三角形+8字模型中有两直角,常用截长补短构造全等
2.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若CE⊥BD于点E,连接AE.求证:∠AEB=45°.
证明:在BE上截取BF=CE,
连接AF.
易证∠ABF=∠ACE,
△ABF≌△ACE(SAS),
得等腰Rt△AFE,
∴∠AEB=45°.
模型2变式 等腰直角三角形及8字模型中只有一个直角,过等腰直角三角形的顶点作垂线构造直角
3.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若∠AEB=45°.求证:CE⊥BD.
证明:过点A作AF⊥AE交BE于点F,得等腰直角△AFE,
△ABF≌△ACE(SAS).
∴∠ABE=∠ACE.
∴∠BEC=∠BAC=90°,
即CE⊥BD.
【变式】 将第3题中的“∠AEB=45°”改为“∠AEC=135°”,第3题中的结论还成立吗?并说明理由.
解:第3题中的结论仍然成立.
理由:如图,过点A作AF⊥AE,交CE的延长线于点F,
则∠BAE=90°+∠CAE=∠CAF.
∵∠AEC=135°,
∴∠AEF=45°.
∴△AEF为等腰直角三角形,AE=AF.
在△BAE和△CAF中,
∴△BAE≌△CAF(SAS).
∴∠BEA=∠CFA=45°.
∴∠BEC=∠AEC-∠BEA=135°-45°=90°,
即CE⊥BE.
补充模型 三垂直模型
4.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为(-1,5).
小专题5 角平分线的综合运用
模型1 双垂线型
1.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC;
(2)如图3,AD平分∠BAC,BD=DC,AC≠AB,求证:∠ABD+∠ACD=180°.
,图1) ,图2) ,图3)
证明:(1)过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠F=∠DEB=90°.
∵∠EBD+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠EBD=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).∴DC=DB.
(2)过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DFC=∠DEB=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).
∴∠ABD=∠DCF.
∵∠DCF+∠ACD=180°,
∴∠ABD+∠ACD=180°.
【变式】 如图,∠CAB=40°,点D为∠CAB的平分线与线段BC的垂直平分线的交点,连接CD,试求∠DCB的度数.
解:过点D作DE⊥AC于点E,DF⊥AB于点F,连接BD.
∵AD平分∠BAC,DE⊥AC,DF⊥AB,
∴DE=DF,∠DEC=∠DFB=90°.
∵∠CAB=40°,∴∠EDF=140°.
∵点D在线段BC的垂直平分线上,
∴DC=DB.
∴Rt△DEC≌Rt△DFB(HL).
∴∠EDC=∠FDB.
∴∠CDB=∠CDF+∠FDB=∠CDF+∠EDC=∠EDF=140°.
∴∠DCB=×(180°-40°)=20°.
模型2 截长补短型
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD.
证明:在BC上截取BF=AB,连接EF.
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE=∠FBE,∠FCE=∠DCE.
在△ABE和△FBE中,
∴△ABE≌△FBE(SAS).∴∠A=∠BFE.
∵AB∥CD,∴∠A+∠D=180°.
∴∠BFE+∠D=180°.
∵∠BFE+∠CFE=180°,∴∠CFE=∠D.
在△FCE和△DCE中,
∴△FCE≌△DCE(AAS).∴CF=CD.
∴BC=BF+CF=AB+CD.
【变式】 已知,在△ABC中,BD为∠ABC的平分线.
(1)如图1,若∠A=100°,∠C=50°,求证:BC=BA+AD;
(2)如图2,若∠BAC=100°,∠C=40°,求证:BC=BD+AD.
图1 图2
证明:(1)在边BC上截取BE=BA,连接DE.
∵BD为∠ABC的平分线,∴∠ABD=∠DBE.
又∵BA=BE,BD=BD,
∴△ABD≌△EBD(SAS).
∴AD=DE,∠A=∠BED.
∵∠A=100°,∴∠BED=100°.
∵∠C=50°,∴∠CDE=50°.∴∠C=∠CDE.
∴DE=CE.∴AD=CE.
∵BC=BE+CE,∴BC=BA+AD.
(2)以BC为边作等边△A′BC,在A′C上截取CD′=BD,连接AA′,AD′.
∵∠BAC=100°,∠ACB=40°,∴∠ABC=40°.
∴∠ABC=∠ACB.∴AB=AC.
∵BD为∠ABC的平分线,
∴∠ABD=∠ABC=20°.
∴△A′BC为等边三角形.
∴A′B=A′C=BC,
∠A′BC=∠A′CB=∠BA′C=60°.
∴∠A′CA=∠A′CB-∠ACB=20°.
∵A′B=A′C,AB=AC,A′A=A′A,
∴△A′BA≌△A′CA(SSS).
∴∠BA′A=∠CA′A=30°.
∵AB=AC,∠ABD=∠ACD′,BD=CD′,
∴△ABD≌△ACD′(SAS).
∴∠BAD=∠CAD′=100°,AD=AD′.
∴∠AD′C=180°-∠CAD′-∠ACD′=60°.
∴∠D′AA′=∠AD′C-∠D′A′A=30°.
∴∠D′AA′=∠DA′A.
∴A′D′=AD′.∴A′D′=AD.
∴BC=A′C=A′D′+CD′=AD+BD.
模型3 延长相交型
3.如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
证明:延长BA,CD相交于点Q.
∵∠CAQ=∠BAE=∠BDC=90°,
∴∠ACQ+∠Q=90°,∠ABE+∠Q=90°.
∴∠ACQ=∠ABE.
在△ABE和△ACQ中,
∴△ABE≌△ACQ(ASA).∴BE=CQ.
∵BD平分∠ABC,∴∠QBD=∠CBD.
∵∠BDC=90°,∴∠BDC=∠BDQ=90°.
在△QDB和△CDB中,
∴△QDB≌△CDB(ASA).∴CD=DQ.
∴BE=CQ=2CD.
模型4 平行等腰型
4.如图,在△ABC中,∠ABC=2∠ACB,AO,BO分别平分∠BAC,∠ABC,连接OC.
(1)求证:OC平分∠ACB;
(2)若AB=6,AC=10,求OB的长.
解:(1)证明:过点O分别作AB,BC,AC的垂线,垂足分别为M,N,E,易得OE=OM=ON,
∴CO平分∠ACB.
(2)过点O作OD∥BC交AC于点D.
∵BO平分∠ABC,∠ABC=2∠ACB,
∴∠ABO=∠ACB.
∵OD∥BC,∴∠ADO=∠ACB.
∴∠ABO=∠ADO.
又∵∠BAO=∠DAO,AO=AO,
∴△BAO≌△DAO(AAS).
∴OB=OD,AD=AB=6.
∴DC=AC-AD=10-6=4.
∵OD∥BC,∴∠DOC=∠OCB=∠ACO.
∴OB=OD=DC=4.
【变式】 如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC.若AN=1,则BC的长为6.
类型1 针对腰长和底边长进行分类
1.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .
2.若实数x,y满足|x-5|+=0,则以x,y的值为边长的等腰三角形的周长为 .
类型2 针对顶角和底角进行分类
3.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
4.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=80°,则它的特征值k= .
5.若等腰三角形中有一个角为52°,则它的一条腰上的高与底边的夹角的度数为 .
类型3 针对锐角、直角和钝角三角形进行分类
6.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为40°,则底角∠B等于( )
A.20° B.60°或20°
C.65°或25° D.60°
7.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其底边上的高是 .
8.已知等腰三角形一腰上的高与另一腰的夹角为36°,求这个等腰三角形的底角的度数.
类型4 确定等腰三角形的数目
9.如图,在平面直角坐标系中,已知A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
A.5 B.6
C.7 D.8
第9题图 第10题图
10.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
A.1个 B.2个
C.3个 D.3个以上
类型5 等腰三角形中的动点问题
11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10 cm,动点P从点A出发沿AB以2 cm/s的速度移动,动点Q从点O出发沿OC以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=或10时,△POQ是等腰三角形.
小专题2 特殊三角形中常用辅助线的作法
类型1 利用等腰三角形“三线合一”作辅助线
方法1 遇到等腰三角形常作底边上的高
1.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于点D,E是AD上一点,且EA=EC,求证:EB⊥AB.
方法2 当等腰三角形中有底边中点时,常连底边上的中线
2.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O为AB的中点,OE⊥OF分别交AC,BC于点E,F.求证:OE=OF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,求CE的长.
类型2 巧用特殊角构造含30°角的直角三角形
方法1 连接两点构造含30°角的直角三角形
4.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,DE=2,则BC的长为 .
方法2 延长两边构造含30°角的直角三角形(补形)
5.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,则CD= .
第5题图 第6题图
方法3 作垂线构造含30°角的直角三角形
6.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF= .
7.如图,在△ABC中,BD是AC边上的中线,BD⊥BC于点B,∠ABD=30°,求证:AB=2BC.
小专题3 构造等腰三角形的常用方法
类型1 利用平行线构造等腰三角形
1.如图,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F,求证:DF=EF.
2.已知△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立?请说明理由.
类型2 运用倍角关系构造等腰三角形
3.如图,在△ABC中,AD平分∠BAC交BC于点D,且∠ABC=2∠C,求证:AB+BD=AC.
类型3 截长补短构造等腰三角形
4.如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数.(用截长法与补短法两种方法解答)
5.如图,在△ABC中,∠ABC=2∠ACB<90°,且AD⊥BC于点D.求证:AB+BD=CD.
小专题4 等腰直角三角形常见的解题模型
模型1 等腰直角三角形+斜边的中点→连接直角顶点和斜边中点
1.如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形.
【变式1】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别在AC,AB上,且DE⊥DF.试判断DE,DF的数量关系,并说明理由.
【变式2】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别为AB,CA延长线上的点,且BE=AF,那么△DEF是否仍为等腰直角三角形?证明你的结论.
模型2 等腰直角三角形+8字模型中有两直角,常用截长补短构造全等
2.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若CE⊥BD于点E,连接AE.求证:∠AEB=45°.
模型2变式 等腰直角三角形及8字模型中只有一个直角,过等腰直角三角形的顶点作垂线构造直角
3.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若∠AEB=45°.求证:CE⊥BD.
【变式】 将第3题中的“∠AEB=45°”改为“∠AEC=135°”,第3题中的结论还成立吗?并说明理由.
补充模型 三垂直模型
4.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
小专题5 角平分线的综合运用
模型1 双垂线型
1.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC;
(2)如图3,AD平分∠BAC,BD=DC,AC≠AB,求证:∠ABD+∠ACD=180°.
,图1) ,图2) ,图3)
【变式】 如图,∠CAB=40°,点D为∠CAB的平分线与线段BC的垂直平分线的交点,连接CD,试求∠DCB的度数.
模型2 截长补短型
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD.
【变式】 已知,在△ABC中,BD为∠ABC的平分线.
(1)如图1,若∠A=100°,∠C=50°,求证:BC=BA+AD;
(2)如图2,若∠BAC=100°,∠C=40°,求证:BC=BD+AD.
图1 图2
模型3 延长相交型
3.如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
模型4 平行等腰型
4.如图,在△ABC中,∠ABC=2∠ACB,AO,BO分别平分∠BAC,∠ABC,连接OC.
(1)求证:OC平分∠ACB;
(2)若AB=6,AC=10,求OB的长.
【变式】 如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC.若AN=1,则BC的长为 .
参考答案:
小专题1 等腰三角形中的分类讨论思想
类型1 针对腰长和底边长进行分类
1.等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是10或11.
2.若实数x,y满足|x-5|+=0,则以x,y的值为边长的等腰三角形的周长为25.
类型2 针对顶角和底角进行分类
3.等腰三角形的一个内角为70°,则另外两个内角的度数分别是(D)
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
4.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=80°,则它的特征值k=或.
5.若等腰三角形中有一个角为52°,则它的一条腰上的高与底边的夹角的度数为26°或38°.
类型3 针对锐角、直角和钝角三角形进行分类
6.在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为40°,则底角∠B等于(C)
A.20° B.60°或20°
C.65°或25° D.60°
7.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为6,则其底边上的高是3或3.
8.已知等腰三角形一腰上的高与另一腰的夹角为36°,求这个等腰三角形的底角的度数.
解:分两种情况讨论:
①若∠A<90°,如图1所示.
∵BD⊥AC,∴∠A+∠ABD=90°.
∵∠ABD=36°,∴∠A=90°-36°=54°.
∵AB=AC,
∴∠ABC=∠C=×(180°-54°)=63°.
②若∠A>90°,如图2所示.
同①可得∠DAB=90°-36°=54°,
∵AB=AC,
∴∠ABC=∠C=∠DAB=27°.
综上所述,等腰三角形底角的度数为63°或27°.
类型4 确定等腰三角形的数目
9.如图,在平面直角坐标系中,已知A(2,2),B(4,0).若在坐标轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是(A)
A.5 B.6
C.7 D.8
第9题图 第10题图
10.如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有(D)
A.1个 B.2个
C.3个 D.3个以上
类型5 等腰三角形中的动点问题
11.如图,∠BOC=60°,点A是BO延长线上的一点,OA=10 cm,动点P从点A出发沿AB以2 cm/s的速度移动,动点Q从点O出发沿OC以1 cm/s的速度移动.如果点P,Q同时出发,用t(s)表示移动的时间,当t=或10时,△POQ是等腰三角形.
小专题2 特殊三角形中常用辅助线的作法
类型1 利用等腰三角形“三线合一”作辅助线
方法1 遇到等腰三角形常作底边上的高
1.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于点D,E是AD上一点,且EA=EC,求证:EB⊥AB.
证明:过点E作EF⊥AC于点F.
∵EA=EC,
∴AF=FC=AC.
∵AC=2AB,∴AF=AB.
∵AD平分∠BAC,∴∠BAD=∠CAD.
在△ABE和△AFE中,
∴△ABE≌△AFE(SAS).
∴∠ABE=∠AFE=90°.∴EB⊥AB.
方法2 当等腰三角形中有底边中点时,常连底边上的中线
2.如图,在Rt△ABC中,AC=BC,∠ACB=90°,点O为AB的中点,OE⊥OF分别交AC,BC于点E,F.求证:OE=OF.
证明:连接OC.
∵AC=BC,∠ACB=90°,点O为AB的中点,
∴∠B=∠ACO=∠BCO=45°,CO⊥AB.
∴OC=OB,∠COB=90°.
又∵∠EOF=90°,∴∠EOC=∠FOB.
在△EOC和△FOB中,
∴△EOC≌△FOB(ASA).∴OE=OF.
3.如图,在△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于点E,AE=2,求CE的长.
解:连接AD.
∵AB=AC,∠BAC=120°,D为BC的中点,
∴∠DAC=∠BAC=60°,∠ADC=90°.
∵DE⊥AC,∴∠ADE=90°-60°=30°.
∴AD=2AE=4.
又∵∠C=90°-∠DAC=30°,
∴AC=2AD=8.
∴CE=AC-AE=8-2=6.
类型2 巧用特殊角构造含30°角的直角三角形
方法1 连接两点构造含30°角的直角三角形
4.如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点D,交AC于点E,DE=2,则BC的长为12.
方法2 延长两边构造含30°角的直角三角形(补形)
5.如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,则CD=2.
第5题图 第6题图
方法3 作垂线构造含30°角的直角三角形
6.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C.若EC=1,则OF=2.
7.如图,在△ABC中,BD是AC边上的中线,BD⊥BC于点B,∠ABD=30°,求证:AB=2BC.
证明:过点A作AM⊥BD,交BD的延长线于点M.
∵在Rt△ABM中,∠ABD=30°,
∴AB=2AM.
∵BD为AC边上的中线,∴AD=CD.
∵DB⊥BC,AM⊥BD,∴∠DBC=∠M=90°.
在△BCD和△MAD中,
∴△BCD≌△MAD(AAS).
∴BC=AM.
∴AB=2BC.
小专题3 构造等腰三角形的常用方法
类型1 利用平行线构造等腰三角形
1.如图,在△ABC中,AB=AC,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于点F,求证:DF=EF.
证明:过点D作DM∥AC,交BC于点M.
∴∠DMB=∠ACB,∠FDM=∠E.
∵AB=AC,∴∠B=∠ACB.
∴∠B=∠DMB.∴BD=MD.
∵BD=CE,∴MD=CE.
在△DMF和△ECF中,
∴△DMF≌△ECF(AAS).
∴DF=EF.
2.已知△ABC为等边三角形,点D为AC上的一个动点,点E为BC延长线上一点,且BD=DE.
(1)如图1,若点D在边AC上,猜想线段AD与CE之间的关系,并说明理由;
(2)如图2,若点D在AC的延长线上,(1)中的结论是否成立?请说明理由.
解:(1)AD=CE.
理由:过点D作DP∥BC,交AB于点P.
∵△ABC是等边三角形,
∴∠APD=∠ABC=∠ACB=∠PDA=60°.
∴△APD也是等边三角形.
∴AP=PD=AD.
∵DB=DE,∴∠DBC=∠DEC.
∵DP∥BC,∴∠PDB=∠CBD.
∴∠PDB=∠DEC.
∵∠BPD=180°-∠APD=120°,∠DCE=180°-∠ACB=120°,∴∠BPD=∠DCE.
在△BPD和△DCE中,
∴△BPD≌△DCE(AAS).
∴PD=CE.∴AD=CE.
(2)AD=CE成立.
理由:过点D作DP∥BC,交AB的延长线于点P.
∵△ABC是等边三角形,
∴∠APD=∠ABC=∠ACB=∠PDC=60°.
∴△APD也是等边三角形.
∴AP=PD=AD.
∵DB=DE,∴∠DBC=∠DEC.
∵DP∥BC,∴∠PDB=∠CBD.
∴∠PDB=∠DEC.
∵∠DCE=∠ACB=60°,
∴∠P=∠DCE.
在△BPD和△DCE中,
∴△BPD≌△DCE(AAS).∴PD=CE.
∴AD=CE.
类型2 运用倍角关系构造等腰三角形
3.如图,在△ABC中,AD平分∠BAC交BC于点D,且∠ABC=2∠C,求证:AB+BD=AC.
证明:方法1:在边AC上截取AP=AB,连接PD.
∵AD是∠BAC的平分线,
∴∠BAD=∠PAD.
在△ABD和△APD中,
∴△ABD≌△APD(SAS).
∴∠B=∠APD,BD=PD.
∵∠B=2∠C,∠APD=∠PDC+∠C,
∴∠PDC=∠C.
∴PD=PC.∴BD=PC.
∴AB+BD=AP+PC=AC.
方法2:延长AB至点E,使BE=BD,连接DE,证△AED≌△ACD即可.
方法3:延长CB至点E,使BE=AB,连接AE,则∠E=∠C=∠EAB,易证∠EAD=∠EDA,∴AC=EA=ED=EB+BD=AB+BD.
类型3 截长补短构造等腰三角形
4.如图,在△ABC中,∠BAC=120°,AD⊥BC于点D,且AB+BD=DC,求∠C的度数.(用截长法与补短法两种方法解答)
解:方法1(截长法):在CD上取点E,使DE=BD,连接AE,则△ADB≌△ADE(SAS),
∴CE=AB=AE.
∴∠B=∠AED=∠C+∠CAE=2∠C.
∵∠BAC=120°,∴∠B+∠C=2∠C+∠C=60°.∴∠C=20°.
方法2(补短法):延长DB至点F,使BF=AB,连接AF,则AB+BD=DF=CD.
∴△ADF≌△ADC(SAS).
∴AF=AC,∠C=∠F=∠ABC.
∵∠BAC=120°,
∴∠ABC+∠C=∠ABC+∠ABC=60°.
∴∠ABC=40°.
∴∠C=20°.
5.如图,在△ABC中,∠ABC=2∠ACB<90°,且AD⊥BC于点D.求证:AB+BD=CD.
证明:方法1(截长法):在CD上取点E,使DE=BD,连接AE,
易证△ABD≌△AED,则AB=AE,∠ABC=∠AED.
∵∠ABC=2∠ACB,
∴∠AED=∠ACB+∠CAE=2∠ACB.
∴∠CAE=∠ACB.
∴AE=EC.
∴AB+BD=EC+DE=CD.
方法2(补短法):延长DB至点F,使BF=AB,连接AF,
由BF=AB可知,∠F=∠FAB,
∴∠ABC=2∠F.
∵∠ABC=2∠ACB,
∴∠F=∠ACB.
易证△ADF≌△ADC,则AB+BD=DF=CD.
小专题4 等腰直角三角形常见的解题模型
模型1 等腰直角三角形+斜边的中点→连接直角顶点和斜边中点
1.如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.求证:△DEF为等腰直角三角形.
证明:连接AD,
∵AB=AC,∠BAC=90°,D为BC中点,
∴AD=BD=CD,∠BAD=∠CAD=∠B=45°,AD⊥BC.
在△BDE和△ADF中,
∴△BDE≌△ADF(SAS).
∴DE=DF,∠BDE=∠ADF.
∵∠BDE+∠ADE=90°,
∴∠ADF+∠ADE=90°,即∠EDF=90°.
∴△EDF为等腰直角三角形.
【变式1】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别在AC,AB上,且DE⊥DF.试判断DE,DF的数量关系,并说明理由.
解:DE=DF,理由如下:
连接AD,∵∠BAC=90°,AB=AC,D为BC中点,
∴CD=AD,∠C=∠DAF=45°,AD⊥BC.
∴∠CDE+∠EDA=∠ADF+∠EDA=90°.
∴∠CDE=∠ADF.
在△CDE和△ADF中,
∴△CDE≌△ADF(ASA).
∴DE=DF.
【变式2】 如图,在△ABC中,∠BAC=90°,AB=AC,D为BC的中点,E,F分别为AB,CA延长线上的点,且BE=AF,那么△DEF是否仍为等腰直角三角形?证明你的结论.
解:△DEF仍为等腰直角三角形.
证明:连接AD,
∵AB=AC,
∴△ABC为等腰三角形.
∵∠BAC=90°,D为BC的中点,
∴AD=BD,AD⊥BC.
∴∠DAC=∠ABD=45°.
∴∠DAF=∠DBE=135°.
又∵AF=BE,
∴△DAF≌△DBE(SAS).
∴FD=ED,∠FDA=∠EDB.
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.
∴△DEF仍为等腰直角三角形.
模型2 等腰直角三角形+8字模型中有两直角,常用截长补短构造全等
2.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若CE⊥BD于点E,连接AE.求证:∠AEB=45°.
证明:在BE上截取BF=CE,
连接AF.
易证∠ABF=∠ACE,
△ABF≌△ACE(SAS),
得等腰Rt△AFE,
∴∠AEB=45°.
模型2变式 等腰直角三角形及8字模型中只有一个直角,过等腰直角三角形的顶点作垂线构造直角
3.如图,△ABC为等腰直角三角形,∠BAC=90°,AB=AC,D是AC上一点.若∠AEB=45°.求证:CE⊥BD.
证明:过点A作AF⊥AE交BE于点F,得等腰直角△AFE,
△ABF≌△ACE(SAS).
∴∠ABE=∠ACE.
∴∠BEC=∠BAC=90°,
即CE⊥BD.
【变式】 将第3题中的“∠AEB=45°”改为“∠AEC=135°”,第3题中的结论还成立吗?并说明理由.
解:第3题中的结论仍然成立.
理由:如图,过点A作AF⊥AE,交CE的延长线于点F,
则∠BAE=90°+∠CAE=∠CAF.
∵∠AEC=135°,
∴∠AEF=45°.
∴△AEF为等腰直角三角形,AE=AF.
在△BAE和△CAF中,
∴△BAE≌△CAF(SAS).
∴∠BEA=∠CFA=45°.
∴∠BEC=∠AEC-∠BEA=135°-45°=90°,
即CE⊥BE.
补充模型 三垂直模型
4.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为(-1,5).
小专题5 角平分线的综合运用
模型1 双垂线型
1.感知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:(1)如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC;
(2)如图3,AD平分∠BAC,BD=DC,AC≠AB,求证:∠ABD+∠ACD=180°.
,图1) ,图2) ,图3)
证明:(1)过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠F=∠DEB=90°.
∵∠EBD+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠EBD=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).∴DC=DB.
(2)过点D作DE⊥AB于点E,DF⊥AC交AC的延长线于点F.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠DFC=∠DEB=90°.
在Rt△DEB和Rt△DFC中,
∴Rt△DEB≌Rt△DFC(HL).
∴∠ABD=∠DCF.
∵∠DCF+∠ACD=180°,
∴∠ABD+∠ACD=180°.
【变式】 如图,∠CAB=40°,点D为∠CAB的平分线与线段BC的垂直平分线的交点,连接CD,试求∠DCB的度数.
解:过点D作DE⊥AC于点E,DF⊥AB于点F,连接BD.
∵AD平分∠BAC,DE⊥AC,DF⊥AB,
∴DE=DF,∠DEC=∠DFB=90°.
∵∠CAB=40°,∴∠EDF=140°.
∵点D在线段BC的垂直平分线上,
∴DC=DB.
∴Rt△DEC≌Rt△DFB(HL).
∴∠EDC=∠FDB.
∴∠CDB=∠CDF+∠FDB=∠CDF+∠EDC=∠EDF=140°.
∴∠DCB=×(180°-40°)=20°.
模型2 截长补短型
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点E在AD上,求证:BC=AB+CD.
证明:在BC上截取BF=AB,连接EF.
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE=∠FBE,∠FCE=∠DCE.
在△ABE和△FBE中,
∴△ABE≌△FBE(SAS).∴∠A=∠BFE.
∵AB∥CD,∴∠A+∠D=180°.
∴∠BFE+∠D=180°.
∵∠BFE+∠CFE=180°,∴∠CFE=∠D.
在△FCE和△DCE中,
∴△FCE≌△DCE(AAS).∴CF=CD.
∴BC=BF+CF=AB+CD.
【变式】 已知,在△ABC中,BD为∠ABC的平分线.
(1)如图1,若∠A=100°,∠C=50°,求证:BC=BA+AD;
(2)如图2,若∠BAC=100°,∠C=40°,求证:BC=BD+AD.
图1 图2
证明:(1)在边BC上截取BE=BA,连接DE.
∵BD为∠ABC的平分线,∴∠ABD=∠DBE.
又∵BA=BE,BD=BD,
∴△ABD≌△EBD(SAS).
∴AD=DE,∠A=∠BED.
∵∠A=100°,∴∠BED=100°.
∵∠C=50°,∴∠CDE=50°.∴∠C=∠CDE.
∴DE=CE.∴AD=CE.
∵BC=BE+CE,∴BC=BA+AD.
(2)以BC为边作等边△A′BC,在A′C上截取CD′=BD,连接AA′,AD′.
∵∠BAC=100°,∠ACB=40°,∴∠ABC=40°.
∴∠ABC=∠ACB.∴AB=AC.
∵BD为∠ABC的平分线,
∴∠ABD=∠ABC=20°.
∴△A′BC为等边三角形.
∴A′B=A′C=BC,
∠A′BC=∠A′CB=∠BA′C=60°.
∴∠A′CA=∠A′CB-∠ACB=20°.
∵A′B=A′C,AB=AC,A′A=A′A,
∴△A′BA≌△A′CA(SSS).
∴∠BA′A=∠CA′A=30°.
∵AB=AC,∠ABD=∠ACD′,BD=CD′,
∴△ABD≌△ACD′(SAS).
∴∠BAD=∠CAD′=100°,AD=AD′.
∴∠AD′C=180°-∠CAD′-∠ACD′=60°.
∴∠D′AA′=∠AD′C-∠D′A′A=30°.
∴∠D′AA′=∠DA′A.
∴A′D′=AD′.∴A′D′=AD.
∴BC=A′C=A′D′+CD′=AD+BD.
模型3 延长相交型
3.如图,在△ABC中,AB=AC,∠A=90°,BE是角平分线,CD⊥BE交BE的延长线于点D,求证:BE=2CD.
证明:延长BA,CD相交于点Q.
∵∠CAQ=∠BAE=∠BDC=90°,
∴∠ACQ+∠Q=90°,∠ABE+∠Q=90°.
∴∠ACQ=∠ABE.
在△ABE和△ACQ中,
∴△ABE≌△ACQ(ASA).∴BE=CQ.
∵BD平分∠ABC,∴∠QBD=∠CBD.
∵∠BDC=90°,∴∠BDC=∠BDQ=90°.
在△QDB和△CDB中,
∴△QDB≌△CDB(ASA).∴CD=DQ.
∴BE=CQ=2CD.
模型4 平行等腰型
4.如图,在△ABC中,∠ABC=2∠ACB,AO,BO分别平分∠BAC,∠ABC,连接OC.
(1)求证:OC平分∠ACB;
(2)若AB=6,AC=10,求OB的长.
解:(1)证明:过点O分别作AB,BC,AC的垂线,垂足分别为M,N,E,易得OE=OM=ON,
∴CO平分∠ACB.
(2)过点O作OD∥BC交AC于点D.
∵BO平分∠ABC,∠ABC=2∠ACB,
∴∠ABO=∠ACB.
∵OD∥BC,∴∠ADO=∠ACB.
∴∠ABO=∠ADO.
又∵∠BAO=∠DAO,AO=AO,
∴△BAO≌△DAO(AAS).
∴OB=OD,AD=AB=6.
∴DC=AC-AD=10-6=4.
∵OD∥BC,∴∠DOC=∠OCB=∠ACO.
∴OB=OD=DC=4.
【变式】 如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC.若AN=1,则BC的长为6.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
