6.4.2向量在物理中的应用举例(教案)-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册
文档属性
| 名称 | 6.4.2向量在物理中的应用举例(教案)-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册 |  | |
| 格式 | doc | ||
| 文件大小 | 243.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 19:39:11 | ||
图片预览

文档简介
第六章 平面向量及其应用
6.4.2 向量在物理中的应用举例
一、教学目标
1. 会用平面向量知识解决简单的物理问题的两种方法-----向量法和坐标法;?
2.体会向量在解决速度、力学等一些简单实际问题中的作用;
3.通过对用向量法解决物理问题的学习,培养学生数学抽象、数学运算、数学建模、数据分析等数学素养。
二、教学重难点
1.用向量方法解决物理问题的基本方法:“四步曲”;
2.能够将物理问题转化为平面向量问题。
三、教学过程:
1、预习自主完成
(1)力与向量的区别
问题1:物理中力是不是就是向量?
①相同点:力和向量都既要考虑 大小 又要考虑 方向 .
②不同点:向量与 始点 无关,力和 作用点 有关,大小和方向相同的两个力,如果作用点不同,那么它们是不相等的.
(2)向量方法在物理中的应用
问题2:物理中力、速度、加速度、位移是向量吗?它们涉及的运算与向量的运算相符合吗?
①力、速度、加速度、位移都是 向量 .
②力、速度、加速度、位移的合成与分解就是向量的 加、减
______运算,运动的叠加亦用到向量的合成.
问题2:物理中还有哪些量对应向量的运算?
③动量mν是 向量的数乘 .
④功即是力F与所产生位移s的 数量积 .
2.探索新知
例1.如图,在重的物体上有两根绳子,绳子与铅垂线的夹角分别为,物体平衡时,求两根绳子拉力的大小.
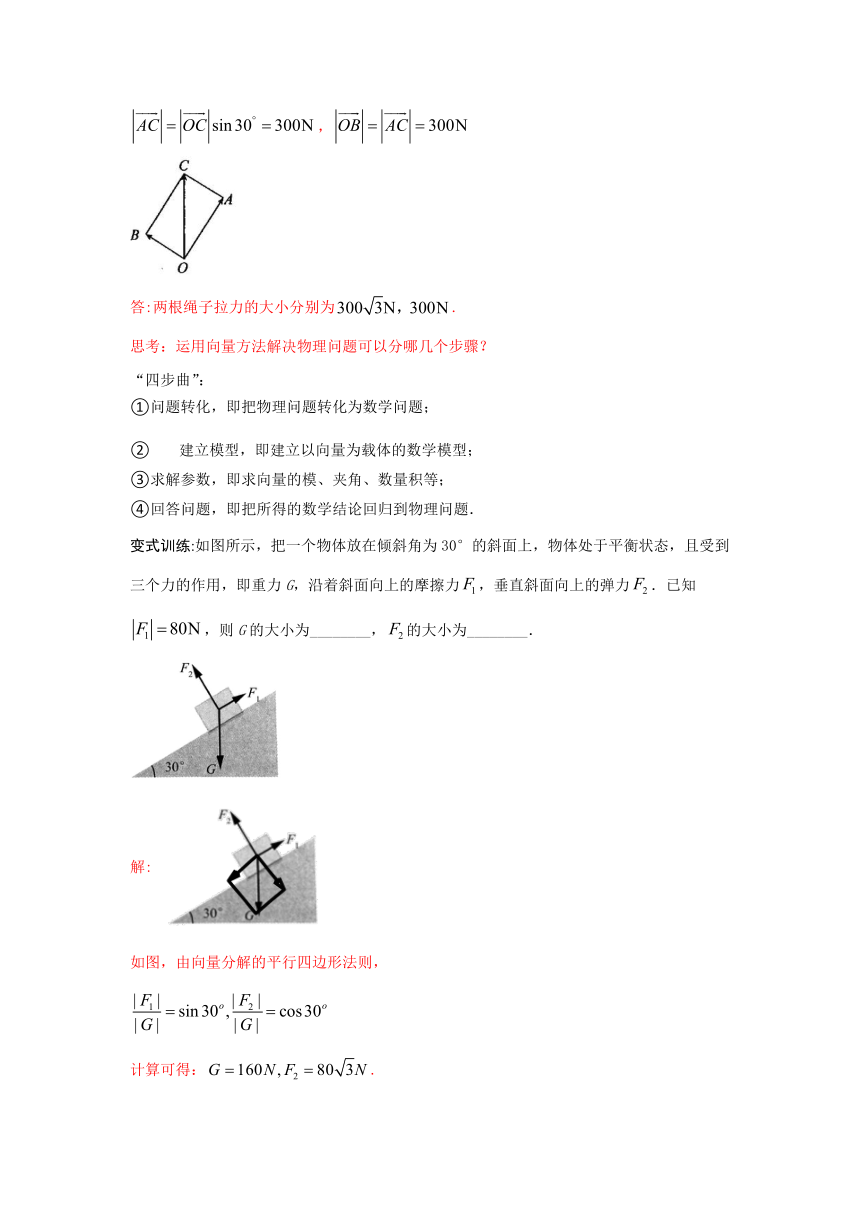
解:作,使.在中,,,,
答:两根绳子拉力的大小分别为.
思考:运用向量方法解决物理问题可以分哪几个步骤?
“四步曲”:
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
④回答问题,即把所得的数学结论回归到物理问题.
变式训练:如图所示,把一个物体放在倾斜角为30°的斜面上,物体处于平衡状态,且受到三个力的作用,即重力G,沿着斜面向上的摩擦力,垂直斜面向上的弹力.已知,则G的大小为________,的大小为________.
解:
如图,由向量分解的平行四边形法则,
计算可得:.
例2.若渡船在静水中的速度大小为,河宽为,水流的速度大小为,则(1)此船渡过该河所用时间的最小值是多少?(2)此船渡过该河的位移最小时,需要多长时间才能从此岸到达彼岸?
解:(1)当船头方向与河岸垂直时,渡河时间最短,
最短时间.
(2)当合速度的方向垂直于河岸时,此船渡过该河的位移最小,
如图所示,水流的速度为,则,船的速度为,则,合速度为,合速度的大小为,则,
设船速与合速度的夹角为,则,
此时.
渡河时间为.
答:此船渡过该河所用时间的最小值是;此船渡过该河的位移最小时,需要才能从此岸到达彼岸.
变式训练:长江流域内某地南北两岸平行,如图所示已知游船在静水中的航行速度的大小,水流的速度的大小,设和所成角为,若游船要从航行到正北方向上位于北岸的码头处,则求的值
解:由题意知有即所以,
答:的值为.
小结:
向量方法解决物理问题“四步曲”;
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
④回答问题,即把所得的数学结论回归到物理问题.
五、作业:习题6.4.1
6.4.2 向量在物理中的应用举例
一、教学目标
1. 会用平面向量知识解决简单的物理问题的两种方法-----向量法和坐标法;?
2.体会向量在解决速度、力学等一些简单实际问题中的作用;
3.通过对用向量法解决物理问题的学习,培养学生数学抽象、数学运算、数学建模、数据分析等数学素养。
二、教学重难点
1.用向量方法解决物理问题的基本方法:“四步曲”;
2.能够将物理问题转化为平面向量问题。
三、教学过程:
1、预习自主完成
(1)力与向量的区别
问题1:物理中力是不是就是向量?
①相同点:力和向量都既要考虑 大小 又要考虑 方向 .
②不同点:向量与 始点 无关,力和 作用点 有关,大小和方向相同的两个力,如果作用点不同,那么它们是不相等的.
(2)向量方法在物理中的应用
问题2:物理中力、速度、加速度、位移是向量吗?它们涉及的运算与向量的运算相符合吗?
①力、速度、加速度、位移都是 向量 .
②力、速度、加速度、位移的合成与分解就是向量的 加、减
______运算,运动的叠加亦用到向量的合成.
问题2:物理中还有哪些量对应向量的运算?
③动量mν是 向量的数乘 .
④功即是力F与所产生位移s的 数量积 .
2.探索新知
例1.如图,在重的物体上有两根绳子,绳子与铅垂线的夹角分别为,物体平衡时,求两根绳子拉力的大小.
解:作,使.在中,,,,
答:两根绳子拉力的大小分别为.
思考:运用向量方法解决物理问题可以分哪几个步骤?
“四步曲”:
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
④回答问题,即把所得的数学结论回归到物理问题.
变式训练:如图所示,把一个物体放在倾斜角为30°的斜面上,物体处于平衡状态,且受到三个力的作用,即重力G,沿着斜面向上的摩擦力,垂直斜面向上的弹力.已知,则G的大小为________,的大小为________.
解:
如图,由向量分解的平行四边形法则,
计算可得:.
例2.若渡船在静水中的速度大小为,河宽为,水流的速度大小为,则(1)此船渡过该河所用时间的最小值是多少?(2)此船渡过该河的位移最小时,需要多长时间才能从此岸到达彼岸?
解:(1)当船头方向与河岸垂直时,渡河时间最短,
最短时间.
(2)当合速度的方向垂直于河岸时,此船渡过该河的位移最小,
如图所示,水流的速度为,则,船的速度为,则,合速度为,合速度的大小为,则,
设船速与合速度的夹角为,则,
此时.
渡河时间为.
答:此船渡过该河所用时间的最小值是;此船渡过该河的位移最小时,需要才能从此岸到达彼岸.
变式训练:长江流域内某地南北两岸平行,如图所示已知游船在静水中的航行速度的大小,水流的速度的大小,设和所成角为,若游船要从航行到正北方向上位于北岸的码头处,则求的值
解:由题意知有即所以,
答:的值为.
小结:
向量方法解决物理问题“四步曲”;
①问题转化,即把物理问题转化为数学问题;
②建立模型,即建立以向量为载体的数学模型;
③求解参数,即求向量的模、夹角、数量积等;
④回答问题,即把所得的数学结论回归到物理问题.
五、作业:习题6.4.1
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
