1.3带电粒子在匀强磁场中的运动 同步练习 word版含答案
文档属性
| 名称 | 1.3带电粒子在匀强磁场中的运动 同步练习 word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 128.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 20:39:59 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.3带电粒子在匀强磁场中的运动
一、单选题
1.平行板电容器两板之间距离为d,接在电压为U的电源上。现有一质量为m,带电量为+q的粒子,以速度v沿水平方向射入两板之间(粒子重力不计),如图所示。若要使粒子能以速度v沿直线匀速穿过,则可以在两板间加(??
)
A.?磁感应强度大小B=
,方向向里的匀强磁场???B.?磁感应强度大小B=
,方向向外的匀强磁场
C.?磁感应强度大小B=Udv,方向向里的匀强磁场????D.?磁感应强度大小B=Udv,方向向外的匀强磁场
2.如图所示,两个相同的带电粒子,不计重力,同时从A孔沿AD方向射入一正方形空腔中,空腔中有垂直纸面向里的匀强磁场,两粒子的运动轨迹分别为a和b,则两粒子的速率和在空腔中运动的时间的关系是(?
)
A.?va=vb
,
tavb
,
ta>tb??????????????C.?va>vb
,
ta,
ta=tb
3.如图所示,一带电粒子沿x轴正方向进入一个垂直纸面向里的匀强磁场中,若要使该粒子所受合外力为零(重力不计),应该加的匀强电场的方向是(??
)
A.?+y方向????????????????????B.?﹣y方向????????????????????C.?﹣x方向????????????????????D.?因不知q的正负,无法确定
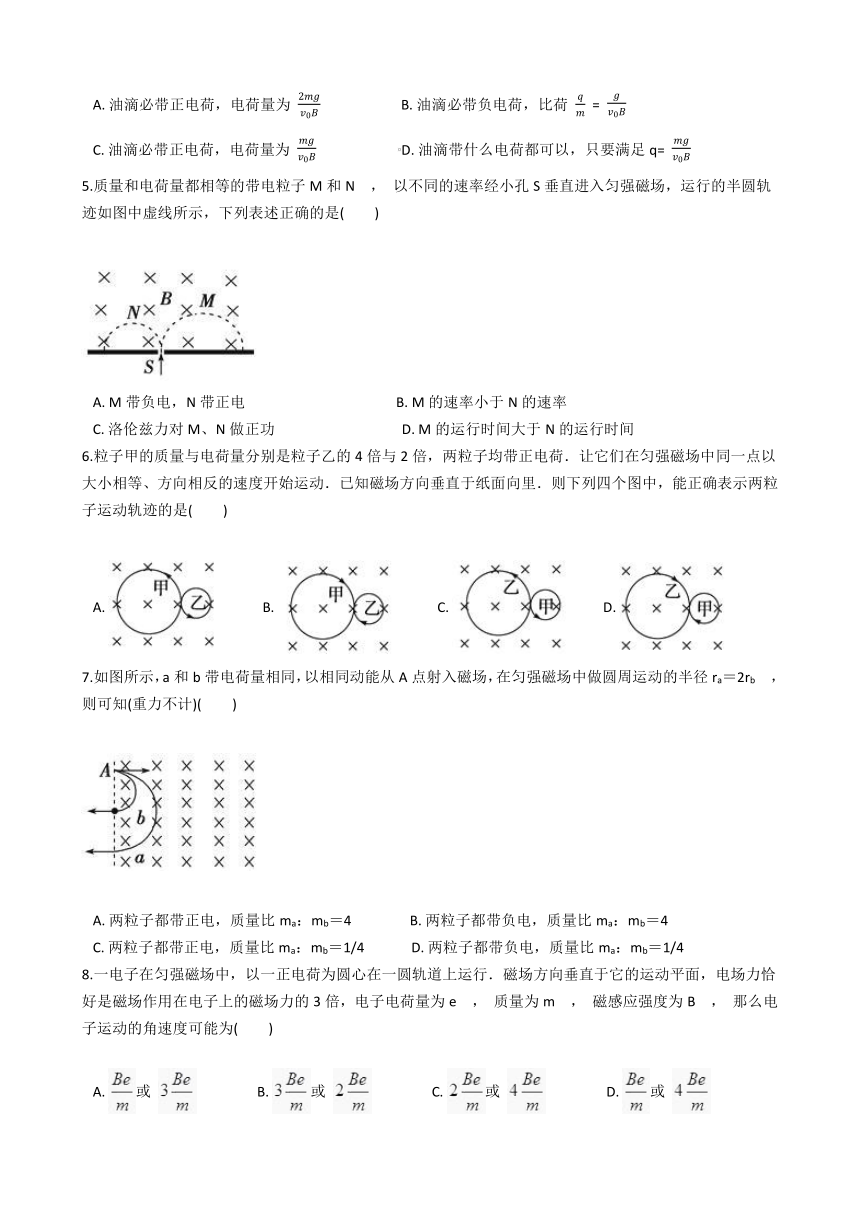
4.带电油滴以水平速度v0垂直进入磁场,并恰好做匀速直线运动,如图所示,若油滴的质量为m,磁感应强度大小为B,则下列说法正确的是(??
)
A.?油滴必带正电荷,电荷量为
???????????????????????B.?油滴必带负电荷,比荷
=
C.?油滴必带正电荷,电荷量为
????????????????????????D.?油滴带什么电荷都可以,只要满足q=
5.质量和电荷量都相等的带电粒子M和N
,
以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
A.?M带负电,N带正电????????????????????????????????????????????B.?M的速率小于N的速率
C.?洛伦兹力对M、N做正功?????????????????????????????????????D.?M的运行时间大于N的运行时间
6.粒子甲的质量与电荷量分别是粒子乙的4倍与2倍,两粒子均带正电荷.让它们在匀强磁场中同一点以大小相等、方向相反的速度开始运动.已知磁场方向垂直于纸面向里.则下列四个图中,能正确表示两粒子运动轨迹的是( )??????????
A.???????????B.???????????C.???????????D.?
7.如图所示,a和b带电荷量相同,以相同动能从A点射入磁场,在匀强磁场中做圆周运动的半径ra=2rb
,
则可知(重力不计)( )
A.?两粒子都带正电,质量比ma:mb=4?????????????????B.?两粒子都带负电,质量比ma:mb=4
C.?两粒子都带正电,质量比ma:mb=1/4?????????????D.?两粒子都带负电,质量比ma:mb=1/4
8.一电子在匀强磁场中,以一正电荷为圆心在一圆轨道上运行.磁场方向垂直于它的运动平面,电场力恰好是磁场作用在电子上的磁场力的3倍,电子电荷量为e
,
质量为m
,
磁感应强度为B
,
那么电子运动的角速度可能为( )
A.?或
?????????????????B.?或
?????????????????C.?或
?????????????????D.?或
9.如图所示,水平导线中有电流I通过,导线正下方的电子初速度的方向与电流I的方向相同,则电子将( )
A.?沿路径a运动,轨迹是圆?????????????????????????????????????B.?沿路径a运动,轨迹半径越来越大
C.?沿路径a运动,轨迹半径越来越小???????????????????????D.?沿路径b运动,轨迹半径越来越小
10.如图,正方形ABCD内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,从B点以不同的速率沿着BC方向射入磁场,粒子a从D点射出,粒子b从AD边的中点E射出,粒子c从AB边的中点F射出。若带电粒子仅受磁场力的作用,下列说法正确的是(??
)
A.?a粒子的速率是b粒子速率的两倍
B.?在磁场中运动的时间,c是a的两倍
C.?在磁场中运动的弧长,a等于c
D.?若c粒子的速率稍微减小,在磁场中的运动时间变短
二、填空题
11.如图所示,一束电子(电量为e)以速度v垂直射入磁感强度为B
,
宽度为d的匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是________,穿透磁场的时间是________。
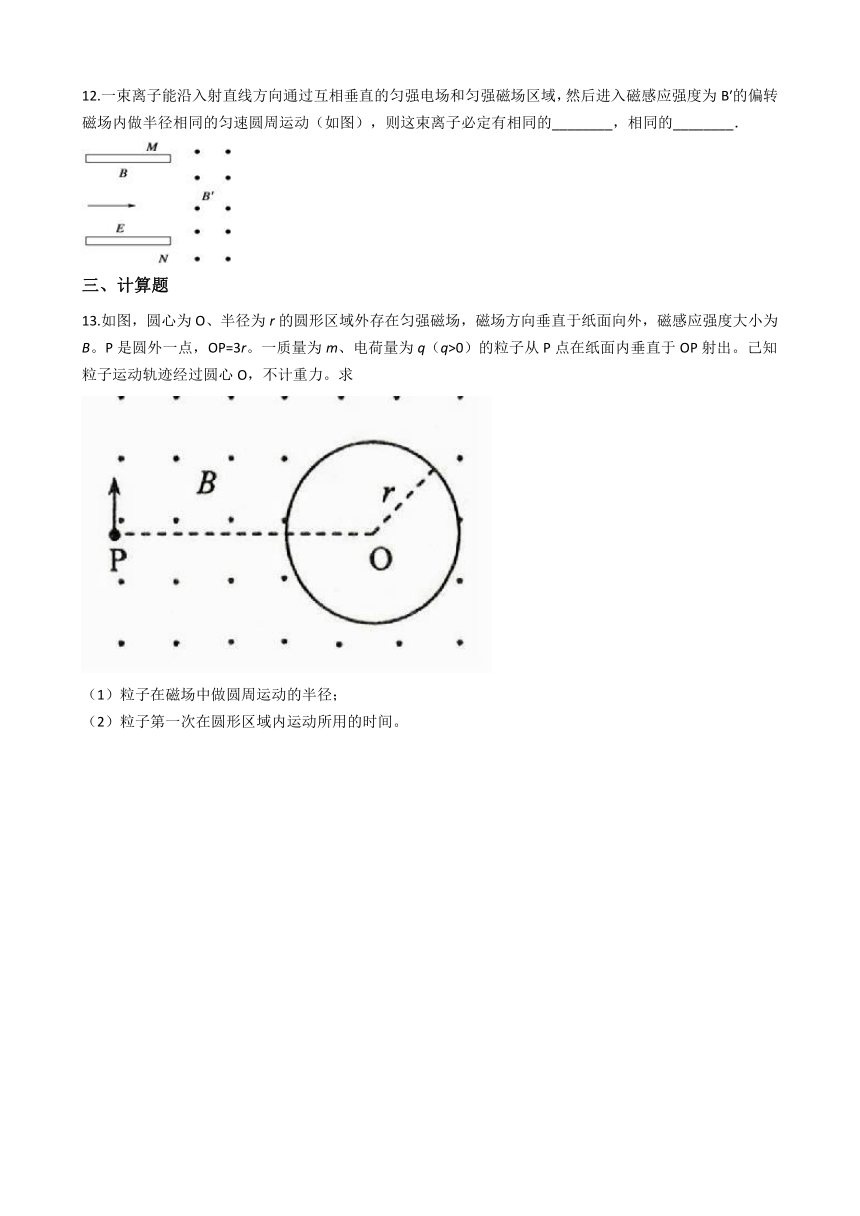
12.一束离子能沿入射直线方向通过互相垂直的匀强电场和匀强磁场区域,然后进入磁感应强度为B′的偏转磁场内做半径相同的匀速圆周运动(如图),则这束离子必定有相同的________,相同的________.
三、计算题
13.如图,圆心为O、半径为r的圆形区域外存在匀强磁场,磁场方向垂直于纸面向外,磁感应强度大小为B。P是圆外一点,OP=3r。一质量为m、电荷量为q(q>0)的粒子从P点在纸面内垂直于OP射出。己知粒子运动轨迹经过圆心O,不计重力。求
(1)粒子在磁场中做圆周运动的半径;
?
(2)粒子第一次在圆形区域内运动所用的时间。
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】若要使粒子能以速度v沿直线匀速穿过,则满足Eq=qvB,解得
;因粒子带正电,所受电场力方向向上,则洛伦兹力向下,由左手定则可知,B的方向向外;B符合题意,ACD不符合题意.
故答案为:B
【分析】粒子要想水平穿过电容器,受到的电场力和洛伦兹力要等大反向,列方程求解磁场强度。
2.【答案】
C
【解析】【解答】由题图可知,半径Ra=2Rb
,
由于带电粒子在匀强磁场中做匀速圆周运动的半径为R=
,又两个带电粒子相同,所以va=2vb。带电粒子在磁场中做匀速圆周运动的周期T=
,则两带电粒子运动的周期相同,设周期为T,从C孔射出的粒子运动的时间ta=
,从B孔射出的粒子运动的时间tb=
,所以tb=2ta
,
故选项C正确。
【分析】分析速度需看半径大小,同种粒子在同一磁场中运动半径大,速度大;运动时间看圆心角,圆心角大,时间长。
3.【答案】
B
【解析】【解答】解:
带电粒子在电场和磁场的复合场中运动,合外力为零,可知所受到的电场力和洛伦兹力大小相等方向相反,假设粒子带正电,由左手定则可知,所受的洛伦兹力的方向沿y轴正方向,则电场力的方向沿y轴的负方向,可知电场方向沿y轴负方向;若粒子带负电,电场力和洛伦兹力方向都将反向,合外力仍为零,电场的方向还是沿y轴负方向.(电场的方向与粒子的电性无关),所以选项B正确,选项ACD错误.
故选B.
【分析】首先根据粒子所受合外力为零,可判断粒子的电场力和洛伦兹力为平衡力,再分别假设粒子带正电或负电,可判知电场的方向,并发现电场的方向与电性无关.
4.【答案】
C
【解析】【解答】解:根据平衡条件知油滴受向上的洛伦兹力,根据左手定则判断油滴必带正电荷;
由受力平衡:qv0B=mg
得:q=
故C正确;
故选:C.
【分析】带电油滴恰好做匀速直线运动,则重力与洛伦兹力等大反向.
5.【答案】
A
【解析】【解答】根据左手定则可知N带正电,M带负电,A正确;
利用洛伦兹力提供向心力
可得
,而M的半径大于N的半径,所以M的速率大于N的速率,B错误;
因为洛伦兹力不做功,C错误;
M和N做圆周运动的周期
,如图所示是半个周期,所以运行时间
,D错误。
故选A
【分析】利用洛伦兹力提供向心力分析计算
。
6.【答案】
A
【解析】【解答】由洛伦兹力f=qvB和牛顿第二定律可得
,
,故
,由左手定则对其运动的方向判断可知A正确。
故选A
【分析】粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力求解半径之比,同时利用左手定则判断洛伦兹力方向。
7.【答案】
B
【解析】【解答】由于qa=qb、Eka=Ekb
,
动能Ek=
mv2和粒子偏转半径
,可得
,所以m与半径r的平方成正比,故ma∶mb=4∶1,由左手定则判知粒子应带负电。
故选B
【分析】粒子在磁场中做圆周运动,利用圆周运动规律求质量之比和左手定则判断带电性质。
8.【答案】
C
【解析】【解答】向心力可能是F电+FB或F电-FB
,
即4eBv1=m
=mωR或2eBv2=m
=mωR;
所以角速度为ω1=
或ω2=
。故C正确。
故选C?
【分析】电子在匀强磁场中做匀速圆周运动,结合圆周运动规律可求解。
9.【答案】
B
【解析】【解答】.由左手定则可判断电子运动轨迹向下弯曲,洛伦兹力提供向心力:
,所以
,B减小,r越来越大,故电子的径迹是a。
故选B
【分析】电子在匀强磁场中做匀速圆周运动,结合圆周运动规律可求解。
10.【答案】
B
【解析】【解答】带电粒子的质量和电荷量都相等,分别设为m和q,由洛伦兹力提供向心力得知
则:v=
找到粒子b的圆心O如图所示,设正方形的边长为d,在△OAE中,
解得:
即
粒子a的半径:Ra=d
粒子c的半径:
A.粒子a和b的速率之比:
A不符合题意;
B.带电粒子在磁场中的运动时间
其中
由几何关系可知,粒子
c的轨迹圆心角为π,粒子a的轨迹圆心角为
,而且两个粒子的周期T一样,故在磁场中运动的时间,c是a的两倍,B符合题意;
C.由弧长公式l=αr可知,
所以在磁场中运动的弧长,a是c的两倍,C不符合题意;
D.由洛伦兹力提供向心力可知,轨迹半径
粒子c的速率稍微减少,半径减少,在磁场中运动仍然可以从AB边射出,轨迹对应的圆心角仍然为π,运动时间为
,其中周期不变,所以c粒子的速率稍微减小,在磁场中的运动时间不变,D不符合题意。
故答案为:B。
【分析】
三个质量和电荷量都相同的带电粒子a、b、c?在方形匀强磁场内做匀速圆周运动,在洛伦兹力提供向心力。根据几何关系可以求得它们各自的轨迹半径。从而求解它们的速率,时间等问题。
二、填空题
11.【答案】;?
【解析】【解答】根据几何关系可知运动半径为r=2d
,
又
,所以
,所以可得电子质量;
根据
得周期
,电子在磁场中转过30°角,所以穿透磁场的时间
。
【分析】带电粒子在磁场中做匀周运动,需要确定半径和圆心角。
12.【答案】速率;比荷
【解析】【解答】解:沿入射方向通过互相垂直的匀强电场和匀强磁场区域,则有电场力与洛伦兹力平衡,即qE=Bqv,解得:v=
;故说明粒子具有相同的速度;
当进入磁感应强度为B的偏转磁场内做半径相同的匀速圆周运动,则有:B′qv=
,解得:R=
,
由于半径相同,则说明离子的比荷相同;
故答案为:速率;比荷.
【分析】通过互相垂直的匀强电场和匀强磁场区域,根据电场力与洛伦兹力平衡,则有相同的速度大小;再由洛伦兹力提供向心力作匀速圆周运动,根据牛顿第二定律,即可求解.
三、计算题
13.【答案】
(1)解:如图,
在三角形OPQ中,根据正弦定理,
,得
。
据几何关系,
,解得
。
(2)解:根据
,得
,
带电粒子在园内做匀速直线运动,
。
【解析】【分析】要使粒子运动轨迹经过圆心O,则应满足
,
作出带电粒子运动轨迹,根据几何关系可得粒子在磁场中做圆周运动的半径R;在磁场中,粒子在洛伦兹力作用下作匀速圆周运动,根据洛伦兹力等于向心力可求v,进而得出粒子在圆中匀速直线运动的时间。
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.3带电粒子在匀强磁场中的运动
一、单选题
1.平行板电容器两板之间距离为d,接在电压为U的电源上。现有一质量为m,带电量为+q的粒子,以速度v沿水平方向射入两板之间(粒子重力不计),如图所示。若要使粒子能以速度v沿直线匀速穿过,则可以在两板间加(??
)
A.?磁感应强度大小B=
,方向向里的匀强磁场???B.?磁感应强度大小B=
,方向向外的匀强磁场
C.?磁感应强度大小B=Udv,方向向里的匀强磁场????D.?磁感应强度大小B=Udv,方向向外的匀强磁场
2.如图所示,两个相同的带电粒子,不计重力,同时从A孔沿AD方向射入一正方形空腔中,空腔中有垂直纸面向里的匀强磁场,两粒子的运动轨迹分别为a和b,则两粒子的速率和在空腔中运动的时间的关系是(?
)
A.?va=vb
,
ta
,
ta>tb??????????????C.?va>vb
,
ta
ta=tb
3.如图所示,一带电粒子沿x轴正方向进入一个垂直纸面向里的匀强磁场中,若要使该粒子所受合外力为零(重力不计),应该加的匀强电场的方向是(??
)
A.?+y方向????????????????????B.?﹣y方向????????????????????C.?﹣x方向????????????????????D.?因不知q的正负,无法确定
4.带电油滴以水平速度v0垂直进入磁场,并恰好做匀速直线运动,如图所示,若油滴的质量为m,磁感应强度大小为B,则下列说法正确的是(??
)
A.?油滴必带正电荷,电荷量为
???????????????????????B.?油滴必带负电荷,比荷
=
C.?油滴必带正电荷,电荷量为
????????????????????????D.?油滴带什么电荷都可以,只要满足q=
5.质量和电荷量都相等的带电粒子M和N
,
以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
A.?M带负电,N带正电????????????????????????????????????????????B.?M的速率小于N的速率
C.?洛伦兹力对M、N做正功?????????????????????????????????????D.?M的运行时间大于N的运行时间
6.粒子甲的质量与电荷量分别是粒子乙的4倍与2倍,两粒子均带正电荷.让它们在匀强磁场中同一点以大小相等、方向相反的速度开始运动.已知磁场方向垂直于纸面向里.则下列四个图中,能正确表示两粒子运动轨迹的是( )??????????
A.???????????B.???????????C.???????????D.?
7.如图所示,a和b带电荷量相同,以相同动能从A点射入磁场,在匀强磁场中做圆周运动的半径ra=2rb
,
则可知(重力不计)( )
A.?两粒子都带正电,质量比ma:mb=4?????????????????B.?两粒子都带负电,质量比ma:mb=4
C.?两粒子都带正电,质量比ma:mb=1/4?????????????D.?两粒子都带负电,质量比ma:mb=1/4
8.一电子在匀强磁场中,以一正电荷为圆心在一圆轨道上运行.磁场方向垂直于它的运动平面,电场力恰好是磁场作用在电子上的磁场力的3倍,电子电荷量为e
,
质量为m
,
磁感应强度为B
,
那么电子运动的角速度可能为( )
A.?或
?????????????????B.?或
?????????????????C.?或
?????????????????D.?或
9.如图所示,水平导线中有电流I通过,导线正下方的电子初速度的方向与电流I的方向相同,则电子将( )
A.?沿路径a运动,轨迹是圆?????????????????????????????????????B.?沿路径a运动,轨迹半径越来越大
C.?沿路径a运动,轨迹半径越来越小???????????????????????D.?沿路径b运动,轨迹半径越来越小
10.如图,正方形ABCD内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,从B点以不同的速率沿着BC方向射入磁场,粒子a从D点射出,粒子b从AD边的中点E射出,粒子c从AB边的中点F射出。若带电粒子仅受磁场力的作用,下列说法正确的是(??
)
A.?a粒子的速率是b粒子速率的两倍
B.?在磁场中运动的时间,c是a的两倍
C.?在磁场中运动的弧长,a等于c
D.?若c粒子的速率稍微减小,在磁场中的运动时间变短
二、填空题
11.如图所示,一束电子(电量为e)以速度v垂直射入磁感强度为B
,
宽度为d的匀强磁场中,穿透磁场时速度方向与电子原来入射方向的夹角是30°,则电子的质量是________,穿透磁场的时间是________。
12.一束离子能沿入射直线方向通过互相垂直的匀强电场和匀强磁场区域,然后进入磁感应强度为B′的偏转磁场内做半径相同的匀速圆周运动(如图),则这束离子必定有相同的________,相同的________.
三、计算题
13.如图,圆心为O、半径为r的圆形区域外存在匀强磁场,磁场方向垂直于纸面向外,磁感应强度大小为B。P是圆外一点,OP=3r。一质量为m、电荷量为q(q>0)的粒子从P点在纸面内垂直于OP射出。己知粒子运动轨迹经过圆心O,不计重力。求
(1)粒子在磁场中做圆周运动的半径;
?
(2)粒子第一次在圆形区域内运动所用的时间。
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】若要使粒子能以速度v沿直线匀速穿过,则满足Eq=qvB,解得
;因粒子带正电,所受电场力方向向上,则洛伦兹力向下,由左手定则可知,B的方向向外;B符合题意,ACD不符合题意.
故答案为:B
【分析】粒子要想水平穿过电容器,受到的电场力和洛伦兹力要等大反向,列方程求解磁场强度。
2.【答案】
C
【解析】【解答】由题图可知,半径Ra=2Rb
,
由于带电粒子在匀强磁场中做匀速圆周运动的半径为R=
,又两个带电粒子相同,所以va=2vb。带电粒子在磁场中做匀速圆周运动的周期T=
,则两带电粒子运动的周期相同,设周期为T,从C孔射出的粒子运动的时间ta=
,从B孔射出的粒子运动的时间tb=
,所以tb=2ta
,
故选项C正确。
【分析】分析速度需看半径大小,同种粒子在同一磁场中运动半径大,速度大;运动时间看圆心角,圆心角大,时间长。
3.【答案】
B
【解析】【解答】解:
带电粒子在电场和磁场的复合场中运动,合外力为零,可知所受到的电场力和洛伦兹力大小相等方向相反,假设粒子带正电,由左手定则可知,所受的洛伦兹力的方向沿y轴正方向,则电场力的方向沿y轴的负方向,可知电场方向沿y轴负方向;若粒子带负电,电场力和洛伦兹力方向都将反向,合外力仍为零,电场的方向还是沿y轴负方向.(电场的方向与粒子的电性无关),所以选项B正确,选项ACD错误.
故选B.
【分析】首先根据粒子所受合外力为零,可判断粒子的电场力和洛伦兹力为平衡力,再分别假设粒子带正电或负电,可判知电场的方向,并发现电场的方向与电性无关.
4.【答案】
C
【解析】【解答】解:根据平衡条件知油滴受向上的洛伦兹力,根据左手定则判断油滴必带正电荷;
由受力平衡:qv0B=mg
得:q=
故C正确;
故选:C.
【分析】带电油滴恰好做匀速直线运动,则重力与洛伦兹力等大反向.
5.【答案】
A
【解析】【解答】根据左手定则可知N带正电,M带负电,A正确;
利用洛伦兹力提供向心力
可得
,而M的半径大于N的半径,所以M的速率大于N的速率,B错误;
因为洛伦兹力不做功,C错误;
M和N做圆周运动的周期
,如图所示是半个周期,所以运行时间
,D错误。
故选A
【分析】利用洛伦兹力提供向心力分析计算
。
6.【答案】
A
【解析】【解答】由洛伦兹力f=qvB和牛顿第二定律可得
,
,故
,由左手定则对其运动的方向判断可知A正确。
故选A
【分析】粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力求解半径之比,同时利用左手定则判断洛伦兹力方向。
7.【答案】
B
【解析】【解答】由于qa=qb、Eka=Ekb
,
动能Ek=
mv2和粒子偏转半径
,可得
,所以m与半径r的平方成正比,故ma∶mb=4∶1,由左手定则判知粒子应带负电。
故选B
【分析】粒子在磁场中做圆周运动,利用圆周运动规律求质量之比和左手定则判断带电性质。
8.【答案】
C
【解析】【解答】向心力可能是F电+FB或F电-FB
,
即4eBv1=m
=mωR或2eBv2=m
=mωR;
所以角速度为ω1=
或ω2=
。故C正确。
故选C?
【分析】电子在匀强磁场中做匀速圆周运动,结合圆周运动规律可求解。
9.【答案】
B
【解析】【解答】.由左手定则可判断电子运动轨迹向下弯曲,洛伦兹力提供向心力:
,所以
,B减小,r越来越大,故电子的径迹是a。
故选B
【分析】电子在匀强磁场中做匀速圆周运动,结合圆周运动规律可求解。
10.【答案】
B
【解析】【解答】带电粒子的质量和电荷量都相等,分别设为m和q,由洛伦兹力提供向心力得知
则:v=
找到粒子b的圆心O如图所示,设正方形的边长为d,在△OAE中,
解得:
即
粒子a的半径:Ra=d
粒子c的半径:
A.粒子a和b的速率之比:
A不符合题意;
B.带电粒子在磁场中的运动时间
其中
由几何关系可知,粒子
c的轨迹圆心角为π,粒子a的轨迹圆心角为
,而且两个粒子的周期T一样,故在磁场中运动的时间,c是a的两倍,B符合题意;
C.由弧长公式l=αr可知,
所以在磁场中运动的弧长,a是c的两倍,C不符合题意;
D.由洛伦兹力提供向心力可知,轨迹半径
粒子c的速率稍微减少,半径减少,在磁场中运动仍然可以从AB边射出,轨迹对应的圆心角仍然为π,运动时间为
,其中周期不变,所以c粒子的速率稍微减小,在磁场中的运动时间不变,D不符合题意。
故答案为:B。
【分析】
三个质量和电荷量都相同的带电粒子a、b、c?在方形匀强磁场内做匀速圆周运动,在洛伦兹力提供向心力。根据几何关系可以求得它们各自的轨迹半径。从而求解它们的速率,时间等问题。
二、填空题
11.【答案】;?
【解析】【解答】根据几何关系可知运动半径为r=2d
,
又
,所以
,所以可得电子质量;
根据
得周期
,电子在磁场中转过30°角,所以穿透磁场的时间
。
【分析】带电粒子在磁场中做匀周运动,需要确定半径和圆心角。
12.【答案】速率;比荷
【解析】【解答】解:沿入射方向通过互相垂直的匀强电场和匀强磁场区域,则有电场力与洛伦兹力平衡,即qE=Bqv,解得:v=
;故说明粒子具有相同的速度;
当进入磁感应强度为B的偏转磁场内做半径相同的匀速圆周运动,则有:B′qv=
,解得:R=
,
由于半径相同,则说明离子的比荷相同;
故答案为:速率;比荷.
【分析】通过互相垂直的匀强电场和匀强磁场区域,根据电场力与洛伦兹力平衡,则有相同的速度大小;再由洛伦兹力提供向心力作匀速圆周运动,根据牛顿第二定律,即可求解.
三、计算题
13.【答案】
(1)解:如图,
在三角形OPQ中,根据正弦定理,
,得
。
据几何关系,
,解得
。
(2)解:根据
,得
,
带电粒子在园内做匀速直线运动,
。
【解析】【分析】要使粒子运动轨迹经过圆心O,则应满足
,
作出带电粒子运动轨迹,根据几何关系可得粒子在磁场中做圆周运动的半径R;在磁场中,粒子在洛伦兹力作用下作匀速圆周运动,根据洛伦兹力等于向心力可求v,进而得出粒子在圆中匀速直线运动的时间。
