2020-2021学年高二下学期物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器 同步练习
文档属性
| 名称 | 2020-2021学年高二下学期物理人教版(2019)选择性必修第二册1.4质谱仪与回旋加速器 同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 343.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 20:38:20 | ||
图片预览




文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.4质谱仪与回旋加速器
一、单选题
1.回旋加速器是加速带电粒子的装置,其核心部分是分别与高频电源的两极相连接的两个D形金属盒,两盒间的狭缝中有周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示。下列说法中正确的是(??
)
A.?只增大金属盒的半径,带电粒子离开加速器时的动能不变
B.?只增大磁场的磁感应强度,带电粒子离开加速器时的动能增大
C.?只增大狭缝间的加速电压,带电粒子离开加速器时的动能增大
D.?只增大狭缝间的加速电压,带电粒子在加速器中运动的时间增大
2.回旋加速器是加速带电粒子的装置。如图所示,其核心部件是分别与高频交流电源两极相连接的两个D形金属盒(
、
),两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,D形盒的半径为R。质量为m、电荷量为q的质子从
盒的质子源(A点)由静止释放,加速到最大动能后经粒子出口处射出。若忽略质子在电场中的加速时间,且不考虑相对论效应,则下列说法正确的是(??
)
A.?交变电压U越大,质子获得的最大动能越大
B.?质子在加速器中的加速次数越多,质子获得的最大动能越大
C.?增大D型盒的半径,质子获得的最大动能增大
D.?质子不断加速,它做圆周运动的周期越来越小
3.关于下列四幅课本上的插图的说法正确的是(??
)
A.?图甲是速度选择器示意图,由图可以判断出带电粒子的电性,不计重力的粒子能够沿直线匀速通过速度选择器的条件是
B.?图乙是磁流体发电机结构示意图,由图可以判断出A极板是发电机的正极
C.?图丙是质谱仪结构示意图,打在底片上的位置越靠近狭缝
说明粒子的比荷越大
D.?图丁是回旋加速器示意图,要使粒子飞出加速器时的动能增大,可仅增加电压U
4.如图所示为某回旋加速器示意图,利用回旋加速器对
粒子进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T,加速电压为U。忽略相对论效应和粒子在D形盒缝隙间的运动时间,下列说法中正确的是(??
)
A.?粒子从磁场中获得能量
B.?保持B,U和T不变,该回旋加速器可以加速质子
C.?只增大加速电压
粒子在回旋加速器中运动的时间变短
D.?只增大加速电压
粒子获得的最大动能增大
5.1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示,这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法不正确的是
(??
)
A.?带电粒子由加速器的中心附近进入加速器????????B.?带电粒子由加速器的边缘进入加速器
C.?电场使带电粒子加速,磁场使带电粒子旋转????D.?离子从D形盒射出时的动能与加速电场的电压无关
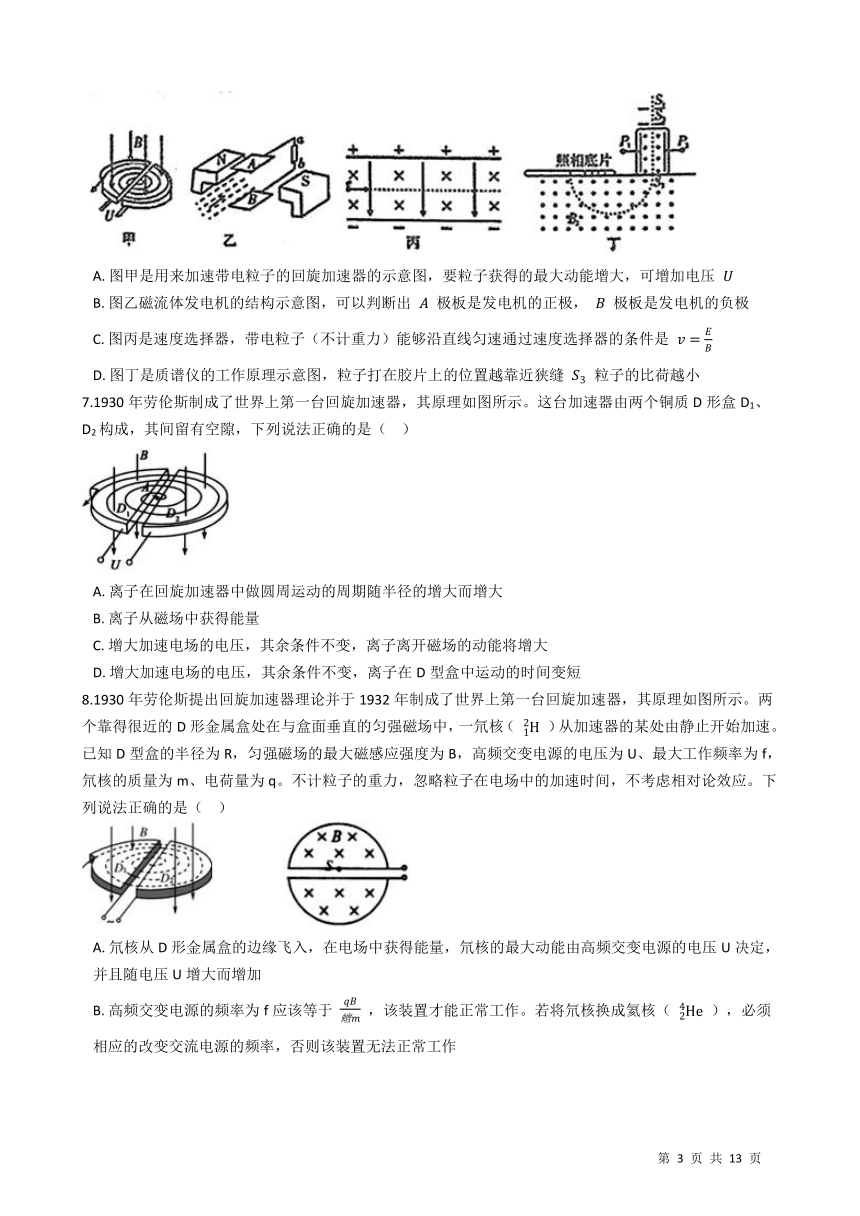
6.下列说法正确的是(??
)
A.?图甲是用来加速带电粒子的回旋加速器的示意图,要粒子获得的最大动能增大,可增加电压
B.?图乙磁流体发电机的结构示意图,可以判断出
极板是发电机的正极,
极板是发电机的负极
C.?图丙是速度选择器,带电粒子(不计重力)能够沿直线匀速通过速度选择器的条件是
D.?图丁是质谱仪的工作原理示意图,粒子打在胶片上的位置越靠近狭缝
粒子的比荷越小
7.1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示。这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法正确的是(??
)
A.?离子在回旋加速器中做圆周运动的周期随半径的增大而增大
B.?离子从磁场中获得能量
C.?增大加速电场的电压,其余条件不变,离子离开磁场的动能将增大
D.?增大加速电场的电压,其余条件不变,离子在D型盒中运动的时间变短
8.1930年劳伦斯提出回旋加速器理论并于1932年制成了世界上第一台回旋加速器,其原理如图所示。两个靠得很近的D形金属盒处在与盒面垂直的匀强磁场中,一氘核(
)从加速器的某处由静止开始加速。已知D型盒的半径为R,匀强磁场的最大磁感应强度为B,高频交变电源的电压为U、最大工作频率为f,氘核的质量为m、电荷量为q。不计粒子的重力,忽略粒子在电场中的加速时间,不考虑相对论效应。下列说法正确的是(??
)
A.?氘核从D形金属盒的边缘飞入,在电场中获得能量,氘核的最大动能由高频交变电源的电压U决定,并且随电压U增大而增加
B.?高频交变电源的频率为f应该等于
,该装置才能正常工作。若将氘核换成氦核(
),必须相应的改变交流电源的频率,否则该装置无法正常工作
C.?氘核第1次加速和第2次加速后在磁场中运动的轨道半径之比为1:2
D.?当
时,氘核的最大动能为
9.如图是回旋加速器的示意图,其核心部分是两个半径为R的D形金属盒,两金属盒表面与磁感应强度为B的匀强磁场垂直,并分别与一个高频电源两端相连.现用它来加速质量为m、电荷量为q的微观粒子(忽略相对论效应),则下列说法正确的是(??
)
A.?要使回旋加速器正常工作,高频电源的频率应为
B.?输出粒子获得的最大动能为
C.?要提高粒子输出时的最大速度,需提高电源的电压
D.?若先后用来加速氘核
和氦核
,则必须调整电源的频率
10.回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个半径为R的D形金属盒,两盒间宽d的狭缝中形成的变化的电场,电压为U;两D形金属盒处于垂直于盒底的匀强磁场B中,一电子利用其加速,则下列说法中正确的是(????
)
A.?电子获得的最大速度为2eBR/m???????????????????????B.?电子获得的最大动能为e2B2R2/(2m)
C.?电子的加速时间为2BdR/U??????????????????????????????D.?增大D形金属盒的半径,电子获得的最大动能减小
二、填空题
11.回旋加速器的构造如图所示,D1、D2是半圆形金属盒,D形盒的缝隙处接交流电源,D形盒处于匀强磁场中。工作时交流电的周期和粒子做圆周运动的周期________(选填“相等”或“不相等”),粒子经电场加速,经磁场回旋,获得的最大动能由________和D形盒的________决定,与加速电压无关。
12.某型号的回旋加速器的工作原理图如图甲所示,图乙为俯视图.回旋加速器的核心部分为D形盒,D形盒置于真空容器中,整个装置放在电磁铁两极之间的磁场中,磁场可以认为是匀强磁场,且与D形盒盒面垂直.两盒间狭缝很小,带电粒子穿过的时间可以忽略不计.带电从粒子源A处进入加速电场的初速度不计,从静止开始加速到出口处所需的时间为t(带电粒子达到最大速度在磁场中完成半个圆周后被导引出来),已知磁场的磁感应强度大小为B,加速器接一高频交流电源,其电压为U,可以使带电粒子每次经过狭缝都能被加速,不考虑相对论效应和重力作用,D形盒半径R=________,D型盒内部带电粒子前三次做匀速圆周的轨道半径之比(由内到外)为________.
三、计算题
13.一台质谱仪的工作原理如图所示.大量的甲、乙两种离子飘入电压力为U0的加速电场,其初速度几乎为0,经过加速后,通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片上.已知甲、乙两种离子的电荷量均为+q,质量分别为2m和m,图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹.不考虑离子间的相互作用.
(1)求甲种离子打在底片上的位置到N点的最小距离x;
(2)在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;
(3)若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】ABC.根据
可得
带电粒子离开加速器时的最大动能
可见带电粒子离开加速器时的最大动能与金属盒之间的电压无关,与D形金属盒内的磁感应强度、及金属盒的半径有关,只增大金属盒的半径,带电粒子离开加速器时的动能增大;只增大磁场的磁感应强度,带电粒子离开加速器时的动能增大,A、C不符合题意,B符合题意;
D.根据
可知,粒子在磁场中做圆周运动的周期与速度大小无关,即粒子在磁场中每半圈的运动时间相同,则粒子在回旋加速器中运动的时间决定于做圆周运动的次数,在磁场中做半圆周运动的次数与加速的次数相同;根据动能定理可得
可得加速次数为
由此可知狭缝间的加速电压越大,加速次数越少,则粒子在回旋加速器中运动的时间越短,D不符合题意;
故答案为:B。
【分析】利用牛顿第二定律结合动能的表达式可以判别最大动能的影响因数;利用周期公式可以判别与速度的大小无关;利用加速电压的大小可以判别加速的次数进而判别运动的时间。
2.【答案】
C
【解析】【解答】AC.质子射出回旋加速器时的速度最大,此时的半径为R,由洛伦兹力提供向心力得
所以当轨道半径最大时,最大速度为
最大动能
质子加速后的最大动能Ek与交变电压U大小无关,A不符合题意,C符合题意;
B.粒子离开回旋加速器的动能是一定的,与加速电压无关;而每次经过电场加速获得的动能为qU,故电压越大,加速的次数n越少,B不符合题意;
D.质子不断加速,它做圆周运动的周期与交变电流的周期相同即不变,D不符合题意。
故答案为:C。
【分析】粒子在磁场中运动时,洛伦兹力提供向心力,满足
,据此求得最大速度;质子被加速后的最大速度与加速电场的电压大小无关;回旋加速器加速粒子使粒子获得的最大动能应该由加速器的半径和磁感应强度B的大小有关;当粒子从D形盒中出来时,速度最大,此时运动的半径等于D形盒的半径?;质子在回旋加速器运动周期T=,
与v大小无关。
3.【答案】
C
【解析】【解答】A.图甲是速度选择器示意图,由图无法判断出带电粒子的电性,不计重力的粒子能够沿直线匀速通过速度选择器的条件是
,A不符合题意;
B.图乙时磁流体发电机结构示意图,由左手定则知正离子向下偏转,所以下极板带正电,A板是电源的负极,B板是电源的正极,B不符合题意;
C.图丙是质谱仪结构示意图,粒子经过速度选择器后的速度一定,根据洛伦兹力提供向心力可得
解得
则可知知R越小,比荷越大,即打在底片上的位置越靠近狭缝
说明粒子的比荷越大,C符合题意;
D.图丁是回旋加速器示意图,根据公式
解得
故最大动能
可知与加速电压无关,D不符合题意。
故答案为:C。
【分析】速度选择器是利用粒子在磁场和电场中受力平衡qvB=qE从而做匀速直线运动,无法判断出电性;根据左手定则判断上下极板的电性进而判断电源正负极;有洛伦兹力提供向心力公式推导比荷决定因素;有洛伦兹力提供向心力公式推导速度公式,可看出比荷一定的粒子速度大小与磁场强度和半径大小有关,与其他因素无关。
?
4.【答案】
C
【解析】【解答】A.粒子在磁场中运动时,磁场的作用只改变粒子的运动方向,不改变粒子的运动速度大小,粒子只在加速电场中获得能量,A不符合题意;
B.粒子在磁场中运动的周期
由于质子
与
粒子的比荷不同,保持B、U和T不变的情况下不能加速质子,B不符合题意;
C.由
解得
粒子射出时的动能
粒子每旋转一周增加的动能是2qU,动能达到Ek时粒子旋转的周数是N,则有
每周的运动时间
则粒子在回旋加速器中的运动时间
若只增大加速电压U,
粒子在回旋加速器中运动的时间变短,C符合题意;
D.设回旋加速器的最大半径是Rm
,
因此粒子在最大半径处运动时速度最大,根据
解得
射出时的最大动能是
若只增大加速电压,由上式可知,
粒子获得的最大动能与加速器的半径、磁感应强度以及电荷的电量和质量有关,与加速电场的电压无关,D不符合题意。
故答案为:C。
【分析】由于洛伦兹力对粒子不做功所以粒子是从交变电场中获得能量;利用周期的表达式可以判别该回旋加速器不能加速质子;利用加速电压的变化可以判别粒子在回旋加速器中运动的时间变短;利用牛顿第二定律可以判别最大动能与加速电压大小无关。
5.【答案】
B
【解析】【解答】AB.根据回旋加速器的加速原理,被加速离子只能由加速器的中心附近进入加速器,从边缘离开加速器,A正确,不符合题意;B错误,符合题意;
C.在磁场中洛伦兹力不做功,离子是从电场中获得能量,C正确,不符合题意;
D.当离子离开回旋加速器时,半径最大,动能最大,则有:
与加速的电压无关,D正确,不符合题意。
故答案为:B。
【分析】带电粒子从加速器的中心附近进入加速器;电场使粒子加速,磁场使粒子偏转;利用牛顿第二定律可以判别最大动能与加速电压大小无关。
6.【答案】
C
【解析】【解答】A.图甲是用来加速带电粒子的回旋加速器的示意图,设
形盒的半径为
,粒子从
形盒射出时,在磁场中的轨道半径等于
形盒的半径,此时粒子的速度最大,动能也达到最大,根据洛伦兹力提供向心力有
,
可得粒子的最大动能为
可知粒子获得的最大动能与电压
无关,A不符合题意;
B.图乙磁流体发电机的结构示意图,根据左手定则可知正离子所受洛伦兹力的方向向下,则可以判断出
极板是发电机的负极,
极板是发电机的正极,B不符合题意;
C.图丙是速度选择器,带电粒子(不计重力)能够沿直线匀速通过速度选择器的条件是
即
C符合题意;
D.图丁是质谱仪的工作原理示意图,由图可知
间是一个速度选择器,所以粒子进入磁场的速度相同,粒子打在胶片上的位置与狭缝
的距离为轨道半径的两倍,设粒子进入磁场的速度为
,则粒子打在胶片上的位置与狭缝
的距离为
则粒子打在胶片上的位置越靠近狭缝
粒子的比荷越大,D不符合题意。
故答案为:C。
【分析】利用牛顿第二定律可以判别粒子最大动能与加速电压的大小无关;利用左手定则可以判别磁流发电机的正负极;利用牛顿第二定律结合粒子在胶片上的位置可以比较比荷的大小。
7.【答案】
D
【解析】【解答】A.离子在回旋加速器中做圆周运动的周期与交变电流的周期相同即不变,A不符合题意;
B.回旋加速器是利用电场加速,粒子获得的能量从电场中获取,B不符合题意;
C.根据
得
最大动能
则离子离开磁场的动能与加速电压无关,C不符合题意;
D.增大加速电场的电压,其余条件不变,每次加速后粒子获得的动能增加,但最终的动能不变,故在磁场中加速的次数减小,带电粒子在D形盒中运动的时间变短,D符合题意。
故答案为:D。
【分析】回旋加速度器中,磁场对粒子进行偏转,洛伦兹力提供向心力,电场对粒子进行加速,根据向心力公式列方程,可以看出粒子的末速度与电场无关,与磁场有关。
8.【答案】
D
【解析】【解答】A.粒子在磁场中做圆周运动,由洛伦兹力提供向心力有
得
当
时,粒子的速度最大,即为
最大动能为
所以粒子的最大动能与电压无关,A不符合题意;
B.当粒子做圆周运动的频率与交流电的频率相等时,装置正常工作,即
B不符合题意;
C.由动能定理可得
粒子加速第1次的速度为
粒子加速第2次的速度为
由公式
可知,半径之比等于速度之比即为
,C不符合题意;
D.当
时,由公式
可知,粒子做圆周运动的频率小于最大工作频率,即装置能正常工作,所以粒子的最大动能为
D符合题意。
故答案为:D。
【分析】利用牛顿第二定律结合动能的表达式可以判别最大动能与电压大小无关;利用粒子运动的周期可以求出交流电的频率大小;利用动能定理结合牛顿第二定律可以求出运动半径之比;利用动能的表达式可以求出最大动能的大小。
9.【答案】
B
【解析】【解答】A、要使回旋加速器正常工作,高频电源的在粒子偏转一周时,电压方向偏转两次,则两次偏转为高频电源的一个周期,则
?,
?,A项错误。
B、输出粒子的最大运动半径为R,即
?得:
?,,粒子的最大动能为
?,B项正确。
C项,由B项
知,要提高粒子输出时的最大速度,需提高磁场强度B或金属盒半径R,提高电源电压只能减小提速时间,不能改变输出时粒子速度大小,C项错误。
D项,由于氘核和氦核的荷质比相同,则两种粒子在金属盒中偏转周期相同,所以不需要调整电源频率,D项错误。
故答案为:B
【分析】回旋加速度器中,磁场对粒子进行偏转,洛伦兹力提供向心力,电场对粒子进行加速,根据向心力公式列方程,可以看出粒子的末速度与电场无关,与磁场有关。
10.【答案】
B
【解析】【解答】粒子离开回旋加速器时满足:
,解得最大速度为:
,最大动能为:
,A不符合题意,B符合题意;粒子在狭缝中运动的距离为s=nd,运动的时间为:
,C不符合题意;由上可知增大D形金属盒的半径,电子获得的最大动能增大,D不符合题意。
故答案为:B
【分析】利用牛顿第二定律可以求出最大的速度和最大的动能;利用位移除以时间可以求出加速运动的时间;利用最大动能和半径的关系可以判别半径变大最大动能变大。
二、填空题
11.【答案】
相等;磁感应强度;半径
【解析】【解答】工作时为了使得带电粒子不断在D型盒的缝隙处被加速,则交流电的周期和粒子做圆周运动的周期相等;]粒子经电场加速,经磁场回旋,由
获得的最大动能
则最大动能由磁感应强度B和D形盒的半径R决定,与加速电压无关。
【分析】利用牛顿第二定律结合动能的表达式可以求出最大动能的影响因数;交变电流的周期和粒子做匀速圆周运动的周期相等。
12.【答案】
;
【解析】【解答】设粒子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v,则
质子圆周运动的周期
质子运动的总时间
t=nT
联立解得
;
设质子第1次经过狭缝被加速后的速度为v1
由动能定理得
由牛顿第二定律有
联立解得:
同理,粒子经2次加速后做圆周运动的半径:
粒子经3次加速后做圆周运动的半径:
可知D型盒内部带电粒子前三次做匀速圆周的轨道半径之比(由内到外)为:
【分析】利用牛顿第二定律可以求出半径的大小;利用牛顿第二定律可以求出轨道半径之比。
三、计算题
13.【答案】
(1)设甲种离子在磁场中的运动半径为r1
电场加速由动能定理得
??????
再由
?
解得
根据几何关系x=2r1﹣L
解得
答:甲种离子打在底片上的位置到N点的最小距离x为
;
(2)最窄处位于过两虚线交点的垂线上
?
?=?1??12?(?2)2
解得
?=2???0??4??0??2?24
答:在答题卡的图中用斜线标出磁场中甲种离子经过的区域如上图所示,该区域最窄处的宽度d为
;
(3)设乙种离子在磁场中的运动半径为
的最小半径
?的最大半径
由题意知
,即
﹣
>L
解得L<
[2
﹣
]
答:若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,狭缝宽度L满足的条件
?????
L<
[2
﹣
]
【解析】【分析】(1)从M进入磁场的粒子打在底片上的位置到N点距离最小,由动能定理求出粒子进入磁场的速度,根据洛伦兹力提供向心力求出轨道半径,由几何关系即可求解甲种离子打在底片上的位置到N点的最小距离x;
(2)就是将一个虚线半圆平移到另一个虚线半圆,最窄处位于过两虚线交点的垂线上,把两个虚线圆心找到,并连接两圆的最高点,两个圆的最高点的距离为L,根据几何关系求解;
(3)从M点射进磁场的最慢甲种离子即加速电压最小时到底片的距离,比从N点射入得最快的乙种离子即加速电压最大时到达底片的距离要大L,两轨迹的直径相差为L,列式即可求解;
(
第
一
页
共
1
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
1.4质谱仪与回旋加速器
一、单选题
1.回旋加速器是加速带电粒子的装置,其核心部分是分别与高频电源的两极相连接的两个D形金属盒,两盒间的狭缝中有周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示。下列说法中正确的是(??
)
A.?只增大金属盒的半径,带电粒子离开加速器时的动能不变
B.?只增大磁场的磁感应强度,带电粒子离开加速器时的动能增大
C.?只增大狭缝间的加速电压,带电粒子离开加速器时的动能增大
D.?只增大狭缝间的加速电压,带电粒子在加速器中运动的时间增大
2.回旋加速器是加速带电粒子的装置。如图所示,其核心部件是分别与高频交流电源两极相连接的两个D形金属盒(
、
),两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,D形盒的半径为R。质量为m、电荷量为q的质子从
盒的质子源(A点)由静止释放,加速到最大动能后经粒子出口处射出。若忽略质子在电场中的加速时间,且不考虑相对论效应,则下列说法正确的是(??
)
A.?交变电压U越大,质子获得的最大动能越大
B.?质子在加速器中的加速次数越多,质子获得的最大动能越大
C.?增大D型盒的半径,质子获得的最大动能增大
D.?质子不断加速,它做圆周运动的周期越来越小
3.关于下列四幅课本上的插图的说法正确的是(??
)
A.?图甲是速度选择器示意图,由图可以判断出带电粒子的电性,不计重力的粒子能够沿直线匀速通过速度选择器的条件是
B.?图乙是磁流体发电机结构示意图,由图可以判断出A极板是发电机的正极
C.?图丙是质谱仪结构示意图,打在底片上的位置越靠近狭缝
说明粒子的比荷越大
D.?图丁是回旋加速器示意图,要使粒子飞出加速器时的动能增大,可仅增加电压U
4.如图所示为某回旋加速器示意图,利用回旋加速器对
粒子进行加速,此时D形盒中的磁场的磁感应强度大小为B,D形盒缝隙间电场变化周期为T,加速电压为U。忽略相对论效应和粒子在D形盒缝隙间的运动时间,下列说法中正确的是(??
)
A.?粒子从磁场中获得能量
B.?保持B,U和T不变,该回旋加速器可以加速质子
C.?只增大加速电压
粒子在回旋加速器中运动的时间变短
D.?只增大加速电压
粒子获得的最大动能增大
5.1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示,这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法不正确的是
(??
)
A.?带电粒子由加速器的中心附近进入加速器????????B.?带电粒子由加速器的边缘进入加速器
C.?电场使带电粒子加速,磁场使带电粒子旋转????D.?离子从D形盒射出时的动能与加速电场的电压无关
6.下列说法正确的是(??
)
A.?图甲是用来加速带电粒子的回旋加速器的示意图,要粒子获得的最大动能增大,可增加电压
B.?图乙磁流体发电机的结构示意图,可以判断出
极板是发电机的正极,
极板是发电机的负极
C.?图丙是速度选择器,带电粒子(不计重力)能够沿直线匀速通过速度选择器的条件是
D.?图丁是质谱仪的工作原理示意图,粒子打在胶片上的位置越靠近狭缝
粒子的比荷越小
7.1930年劳伦斯制成了世界上第一台回旋加速器,其原理如图所示。这台加速器由两个铜质D形盒D1、D2构成,其间留有空隙,下列说法正确的是(??
)
A.?离子在回旋加速器中做圆周运动的周期随半径的增大而增大
B.?离子从磁场中获得能量
C.?增大加速电场的电压,其余条件不变,离子离开磁场的动能将增大
D.?增大加速电场的电压,其余条件不变,离子在D型盒中运动的时间变短
8.1930年劳伦斯提出回旋加速器理论并于1932年制成了世界上第一台回旋加速器,其原理如图所示。两个靠得很近的D形金属盒处在与盒面垂直的匀强磁场中,一氘核(
)从加速器的某处由静止开始加速。已知D型盒的半径为R,匀强磁场的最大磁感应强度为B,高频交变电源的电压为U、最大工作频率为f,氘核的质量为m、电荷量为q。不计粒子的重力,忽略粒子在电场中的加速时间,不考虑相对论效应。下列说法正确的是(??
)
A.?氘核从D形金属盒的边缘飞入,在电场中获得能量,氘核的最大动能由高频交变电源的电压U决定,并且随电压U增大而增加
B.?高频交变电源的频率为f应该等于
,该装置才能正常工作。若将氘核换成氦核(
),必须相应的改变交流电源的频率,否则该装置无法正常工作
C.?氘核第1次加速和第2次加速后在磁场中运动的轨道半径之比为1:2
D.?当
时,氘核的最大动能为
9.如图是回旋加速器的示意图,其核心部分是两个半径为R的D形金属盒,两金属盒表面与磁感应强度为B的匀强磁场垂直,并分别与一个高频电源两端相连.现用它来加速质量为m、电荷量为q的微观粒子(忽略相对论效应),则下列说法正确的是(??
)
A.?要使回旋加速器正常工作,高频电源的频率应为
B.?输出粒子获得的最大动能为
C.?要提高粒子输出时的最大速度,需提高电源的电压
D.?若先后用来加速氘核
和氦核
,则必须调整电源的频率
10.回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电极相连接的两个半径为R的D形金属盒,两盒间宽d的狭缝中形成的变化的电场,电压为U;两D形金属盒处于垂直于盒底的匀强磁场B中,一电子利用其加速,则下列说法中正确的是(????
)
A.?电子获得的最大速度为2eBR/m???????????????????????B.?电子获得的最大动能为e2B2R2/(2m)
C.?电子的加速时间为2BdR/U??????????????????????????????D.?增大D形金属盒的半径,电子获得的最大动能减小
二、填空题
11.回旋加速器的构造如图所示,D1、D2是半圆形金属盒,D形盒的缝隙处接交流电源,D形盒处于匀强磁场中。工作时交流电的周期和粒子做圆周运动的周期________(选填“相等”或“不相等”),粒子经电场加速,经磁场回旋,获得的最大动能由________和D形盒的________决定,与加速电压无关。
12.某型号的回旋加速器的工作原理图如图甲所示,图乙为俯视图.回旋加速器的核心部分为D形盒,D形盒置于真空容器中,整个装置放在电磁铁两极之间的磁场中,磁场可以认为是匀强磁场,且与D形盒盒面垂直.两盒间狭缝很小,带电粒子穿过的时间可以忽略不计.带电从粒子源A处进入加速电场的初速度不计,从静止开始加速到出口处所需的时间为t(带电粒子达到最大速度在磁场中完成半个圆周后被导引出来),已知磁场的磁感应强度大小为B,加速器接一高频交流电源,其电压为U,可以使带电粒子每次经过狭缝都能被加速,不考虑相对论效应和重力作用,D形盒半径R=________,D型盒内部带电粒子前三次做匀速圆周的轨道半径之比(由内到外)为________.
三、计算题
13.一台质谱仪的工作原理如图所示.大量的甲、乙两种离子飘入电压力为U0的加速电场,其初速度几乎为0,经过加速后,通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片上.已知甲、乙两种离子的电荷量均为+q,质量分别为2m和m,图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹.不考虑离子间的相互作用.
(1)求甲种离子打在底片上的位置到N点的最小距离x;
(2)在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;
(3)若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.
答案解析部分
一、单选题
1.【答案】
B
【解析】【解答】ABC.根据
可得
带电粒子离开加速器时的最大动能
可见带电粒子离开加速器时的最大动能与金属盒之间的电压无关,与D形金属盒内的磁感应强度、及金属盒的半径有关,只增大金属盒的半径,带电粒子离开加速器时的动能增大;只增大磁场的磁感应强度,带电粒子离开加速器时的动能增大,A、C不符合题意,B符合题意;
D.根据
可知,粒子在磁场中做圆周运动的周期与速度大小无关,即粒子在磁场中每半圈的运动时间相同,则粒子在回旋加速器中运动的时间决定于做圆周运动的次数,在磁场中做半圆周运动的次数与加速的次数相同;根据动能定理可得
可得加速次数为
由此可知狭缝间的加速电压越大,加速次数越少,则粒子在回旋加速器中运动的时间越短,D不符合题意;
故答案为:B。
【分析】利用牛顿第二定律结合动能的表达式可以判别最大动能的影响因数;利用周期公式可以判别与速度的大小无关;利用加速电压的大小可以判别加速的次数进而判别运动的时间。
2.【答案】
C
【解析】【解答】AC.质子射出回旋加速器时的速度最大,此时的半径为R,由洛伦兹力提供向心力得
所以当轨道半径最大时,最大速度为
最大动能
质子加速后的最大动能Ek与交变电压U大小无关,A不符合题意,C符合题意;
B.粒子离开回旋加速器的动能是一定的,与加速电压无关;而每次经过电场加速获得的动能为qU,故电压越大,加速的次数n越少,B不符合题意;
D.质子不断加速,它做圆周运动的周期与交变电流的周期相同即不变,D不符合题意。
故答案为:C。
【分析】粒子在磁场中运动时,洛伦兹力提供向心力,满足
,据此求得最大速度;质子被加速后的最大速度与加速电场的电压大小无关;回旋加速器加速粒子使粒子获得的最大动能应该由加速器的半径和磁感应强度B的大小有关;当粒子从D形盒中出来时,速度最大,此时运动的半径等于D形盒的半径?;质子在回旋加速器运动周期T=,
与v大小无关。
3.【答案】
C
【解析】【解答】A.图甲是速度选择器示意图,由图无法判断出带电粒子的电性,不计重力的粒子能够沿直线匀速通过速度选择器的条件是
,A不符合题意;
B.图乙时磁流体发电机结构示意图,由左手定则知正离子向下偏转,所以下极板带正电,A板是电源的负极,B板是电源的正极,B不符合题意;
C.图丙是质谱仪结构示意图,粒子经过速度选择器后的速度一定,根据洛伦兹力提供向心力可得
解得
则可知知R越小,比荷越大,即打在底片上的位置越靠近狭缝
说明粒子的比荷越大,C符合题意;
D.图丁是回旋加速器示意图,根据公式
解得
故最大动能
可知与加速电压无关,D不符合题意。
故答案为:C。
【分析】速度选择器是利用粒子在磁场和电场中受力平衡qvB=qE从而做匀速直线运动,无法判断出电性;根据左手定则判断上下极板的电性进而判断电源正负极;有洛伦兹力提供向心力公式推导比荷决定因素;有洛伦兹力提供向心力公式推导速度公式,可看出比荷一定的粒子速度大小与磁场强度和半径大小有关,与其他因素无关。
?
4.【答案】
C
【解析】【解答】A.粒子在磁场中运动时,磁场的作用只改变粒子的运动方向,不改变粒子的运动速度大小,粒子只在加速电场中获得能量,A不符合题意;
B.粒子在磁场中运动的周期
由于质子
与
粒子的比荷不同,保持B、U和T不变的情况下不能加速质子,B不符合题意;
C.由
解得
粒子射出时的动能
粒子每旋转一周增加的动能是2qU,动能达到Ek时粒子旋转的周数是N,则有
每周的运动时间
则粒子在回旋加速器中的运动时间
若只增大加速电压U,
粒子在回旋加速器中运动的时间变短,C符合题意;
D.设回旋加速器的最大半径是Rm
,
因此粒子在最大半径处运动时速度最大,根据
解得
射出时的最大动能是
若只增大加速电压,由上式可知,
粒子获得的最大动能与加速器的半径、磁感应强度以及电荷的电量和质量有关,与加速电场的电压无关,D不符合题意。
故答案为:C。
【分析】由于洛伦兹力对粒子不做功所以粒子是从交变电场中获得能量;利用周期的表达式可以判别该回旋加速器不能加速质子;利用加速电压的变化可以判别粒子在回旋加速器中运动的时间变短;利用牛顿第二定律可以判别最大动能与加速电压大小无关。
5.【答案】
B
【解析】【解答】AB.根据回旋加速器的加速原理,被加速离子只能由加速器的中心附近进入加速器,从边缘离开加速器,A正确,不符合题意;B错误,符合题意;
C.在磁场中洛伦兹力不做功,离子是从电场中获得能量,C正确,不符合题意;
D.当离子离开回旋加速器时,半径最大,动能最大,则有:
与加速的电压无关,D正确,不符合题意。
故答案为:B。
【分析】带电粒子从加速器的中心附近进入加速器;电场使粒子加速,磁场使粒子偏转;利用牛顿第二定律可以判别最大动能与加速电压大小无关。
6.【答案】
C
【解析】【解答】A.图甲是用来加速带电粒子的回旋加速器的示意图,设
形盒的半径为
,粒子从
形盒射出时,在磁场中的轨道半径等于
形盒的半径,此时粒子的速度最大,动能也达到最大,根据洛伦兹力提供向心力有
,
可得粒子的最大动能为
可知粒子获得的最大动能与电压
无关,A不符合题意;
B.图乙磁流体发电机的结构示意图,根据左手定则可知正离子所受洛伦兹力的方向向下,则可以判断出
极板是发电机的负极,
极板是发电机的正极,B不符合题意;
C.图丙是速度选择器,带电粒子(不计重力)能够沿直线匀速通过速度选择器的条件是
即
C符合题意;
D.图丁是质谱仪的工作原理示意图,由图可知
间是一个速度选择器,所以粒子进入磁场的速度相同,粒子打在胶片上的位置与狭缝
的距离为轨道半径的两倍,设粒子进入磁场的速度为
,则粒子打在胶片上的位置与狭缝
的距离为
则粒子打在胶片上的位置越靠近狭缝
粒子的比荷越大,D不符合题意。
故答案为:C。
【分析】利用牛顿第二定律可以判别粒子最大动能与加速电压的大小无关;利用左手定则可以判别磁流发电机的正负极;利用牛顿第二定律结合粒子在胶片上的位置可以比较比荷的大小。
7.【答案】
D
【解析】【解答】A.离子在回旋加速器中做圆周运动的周期与交变电流的周期相同即不变,A不符合题意;
B.回旋加速器是利用电场加速,粒子获得的能量从电场中获取,B不符合题意;
C.根据
得
最大动能
则离子离开磁场的动能与加速电压无关,C不符合题意;
D.增大加速电场的电压,其余条件不变,每次加速后粒子获得的动能增加,但最终的动能不变,故在磁场中加速的次数减小,带电粒子在D形盒中运动的时间变短,D符合题意。
故答案为:D。
【分析】回旋加速度器中,磁场对粒子进行偏转,洛伦兹力提供向心力,电场对粒子进行加速,根据向心力公式列方程,可以看出粒子的末速度与电场无关,与磁场有关。
8.【答案】
D
【解析】【解答】A.粒子在磁场中做圆周运动,由洛伦兹力提供向心力有
得
当
时,粒子的速度最大,即为
最大动能为
所以粒子的最大动能与电压无关,A不符合题意;
B.当粒子做圆周运动的频率与交流电的频率相等时,装置正常工作,即
B不符合题意;
C.由动能定理可得
粒子加速第1次的速度为
粒子加速第2次的速度为
由公式
可知,半径之比等于速度之比即为
,C不符合题意;
D.当
时,由公式
可知,粒子做圆周运动的频率小于最大工作频率,即装置能正常工作,所以粒子的最大动能为
D符合题意。
故答案为:D。
【分析】利用牛顿第二定律结合动能的表达式可以判别最大动能与电压大小无关;利用粒子运动的周期可以求出交流电的频率大小;利用动能定理结合牛顿第二定律可以求出运动半径之比;利用动能的表达式可以求出最大动能的大小。
9.【答案】
B
【解析】【解答】A、要使回旋加速器正常工作,高频电源的在粒子偏转一周时,电压方向偏转两次,则两次偏转为高频电源的一个周期,则
?,
?,A项错误。
B、输出粒子的最大运动半径为R,即
?得:
?,,粒子的最大动能为
?,B项正确。
C项,由B项
知,要提高粒子输出时的最大速度,需提高磁场强度B或金属盒半径R,提高电源电压只能减小提速时间,不能改变输出时粒子速度大小,C项错误。
D项,由于氘核和氦核的荷质比相同,则两种粒子在金属盒中偏转周期相同,所以不需要调整电源频率,D项错误。
故答案为:B
【分析】回旋加速度器中,磁场对粒子进行偏转,洛伦兹力提供向心力,电场对粒子进行加速,根据向心力公式列方程,可以看出粒子的末速度与电场无关,与磁场有关。
10.【答案】
B
【解析】【解答】粒子离开回旋加速器时满足:
,解得最大速度为:
,最大动能为:
,A不符合题意,B符合题意;粒子在狭缝中运动的距离为s=nd,运动的时间为:
,C不符合题意;由上可知增大D形金属盒的半径,电子获得的最大动能增大,D不符合题意。
故答案为:B
【分析】利用牛顿第二定律可以求出最大的速度和最大的动能;利用位移除以时间可以求出加速运动的时间;利用最大动能和半径的关系可以判别半径变大最大动能变大。
二、填空题
11.【答案】
相等;磁感应强度;半径
【解析】【解答】工作时为了使得带电粒子不断在D型盒的缝隙处被加速,则交流电的周期和粒子做圆周运动的周期相等;]粒子经电场加速,经磁场回旋,由
获得的最大动能
则最大动能由磁感应强度B和D形盒的半径R决定,与加速电压无关。
【分析】利用牛顿第二定律结合动能的表达式可以求出最大动能的影响因数;交变电流的周期和粒子做匀速圆周运动的周期相等。
12.【答案】
;
【解析】【解答】设粒子从静止开始加速到出口处运动了n圈,质子在出口处的速度为v,则
质子圆周运动的周期
质子运动的总时间
t=nT
联立解得
;
设质子第1次经过狭缝被加速后的速度为v1
由动能定理得
由牛顿第二定律有
联立解得:
同理,粒子经2次加速后做圆周运动的半径:
粒子经3次加速后做圆周运动的半径:
可知D型盒内部带电粒子前三次做匀速圆周的轨道半径之比(由内到外)为:
【分析】利用牛顿第二定律可以求出半径的大小;利用牛顿第二定律可以求出轨道半径之比。
三、计算题
13.【答案】
(1)设甲种离子在磁场中的运动半径为r1
电场加速由动能定理得
??????
再由
?
解得
根据几何关系x=2r1﹣L
解得
答:甲种离子打在底片上的位置到N点的最小距离x为
;
(2)最窄处位于过两虚线交点的垂线上
?
?=?1??12?(?2)2
解得
?=2???0??4??0??2?24
答:在答题卡的图中用斜线标出磁场中甲种离子经过的区域如上图所示,该区域最窄处的宽度d为
;
(3)设乙种离子在磁场中的运动半径为
的最小半径
?的最大半径
由题意知
,即
﹣
>L
解得L<
[2
﹣
]
答:若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,狭缝宽度L满足的条件
?????
L<
[2
﹣
]
【解析】【分析】(1)从M进入磁场的粒子打在底片上的位置到N点距离最小,由动能定理求出粒子进入磁场的速度,根据洛伦兹力提供向心力求出轨道半径,由几何关系即可求解甲种离子打在底片上的位置到N点的最小距离x;
(2)就是将一个虚线半圆平移到另一个虚线半圆,最窄处位于过两虚线交点的垂线上,把两个虚线圆心找到,并连接两圆的最高点,两个圆的最高点的距离为L,根据几何关系求解;
(3)从M点射进磁场的最慢甲种离子即加速电压最小时到底片的距离,比从N点射入得最快的乙种离子即加速电压最大时到达底片的距离要大L,两轨迹的直径相差为L,列式即可求解;
(
第
一
页
共
1
页
)
