19.1.1平行四边形的性质(第1课时)
文档属性
| 名称 | 19.1.1平行四边形的性质(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 344.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-22 19:53:48 | ||
图片预览





文档简介
(共27张PPT)
第一课时
教学目标:
理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
培养学生发现问题、解决问题的能力及逻辑推理能力.
教学重点:
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
教学难点:
运用平行四边形的性质进行有关的论证和计算.
知识回顾:
思考:平行线性质、全等三角形的性质及判定和四边形的概念是什么?
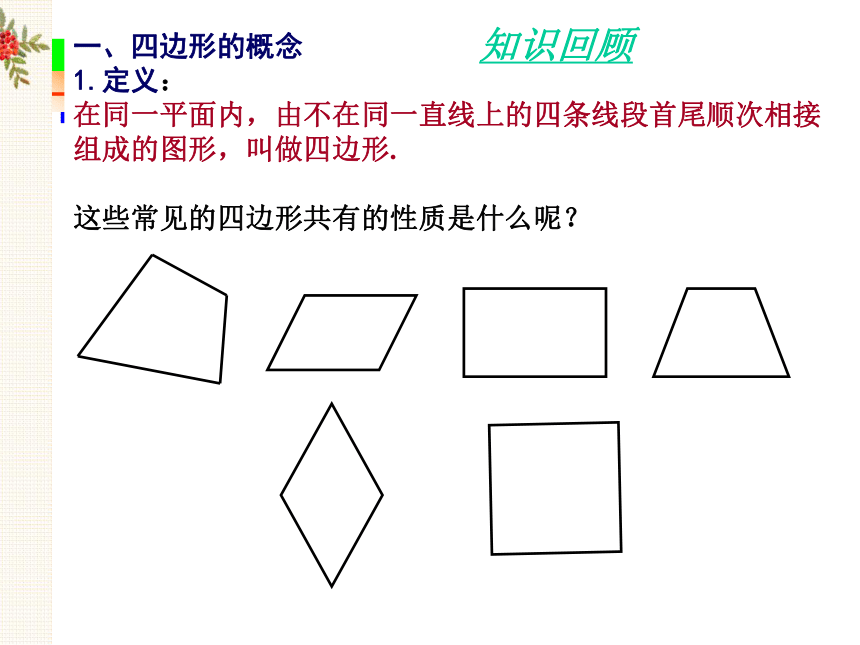
一、四边形的概念
1.定义:
在同一平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形,叫做四边形.
这些常见的四边形共有的性质是什么呢?
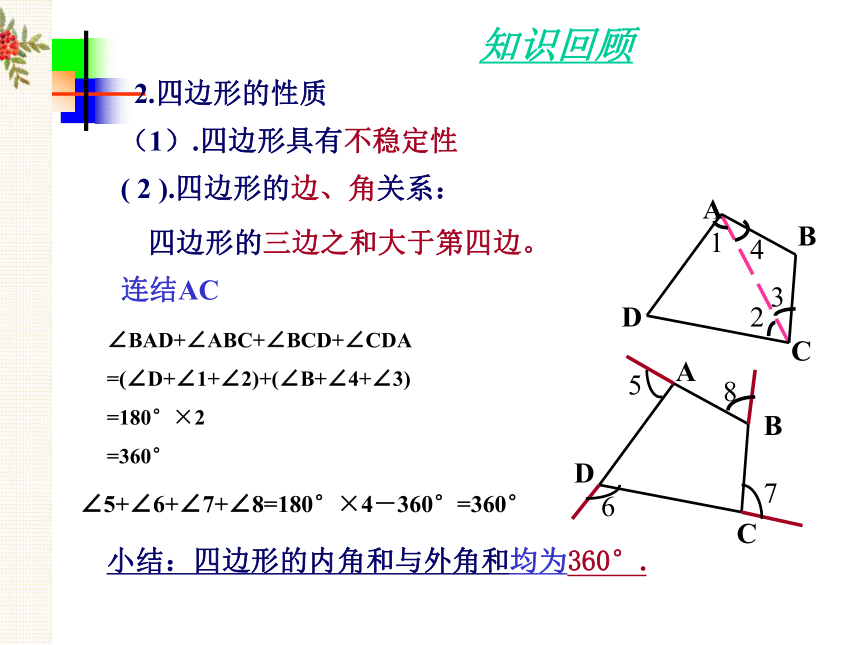
知识回顾
( 2 ).四边形的边、角关系:
(1).四边形具有不稳定性
A
D
C
B
4
3
2
1
∠BAD+∠ABC+∠BCD+∠CDA
=(∠D+∠1+∠2)+(∠B+∠4+∠3)
=180°×2
=360°
D
C
B
A
8
7
6
5
∠5+∠6+∠7+∠8=180°×4-360°=360°
小结:四边形的内角和与外角和均为360°.
知识回顾
2.四边形的性质
四边形的三边之和大于第四边。
连结AC
知识回顾
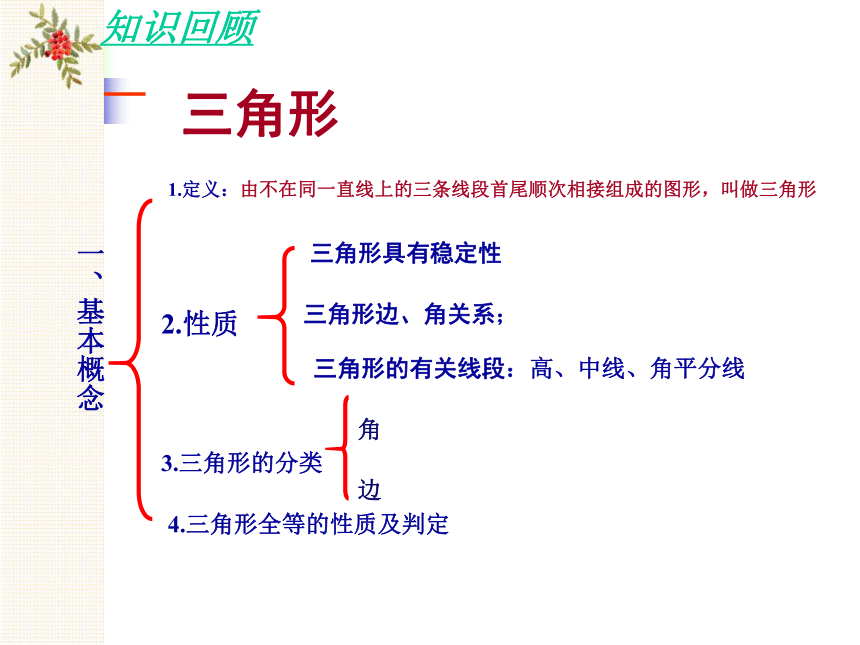
一、基本概念
1.定义:由不在同一直线上的三条线段首尾顺次相接组成的图形,叫做三角形
三角形边、角关系;
三角形的有关线段:高、中线、角平分线
三角形具有稳定性
3.三角形的分类
4.三角形全等的性质及判定
三角形
2.性质
角
边
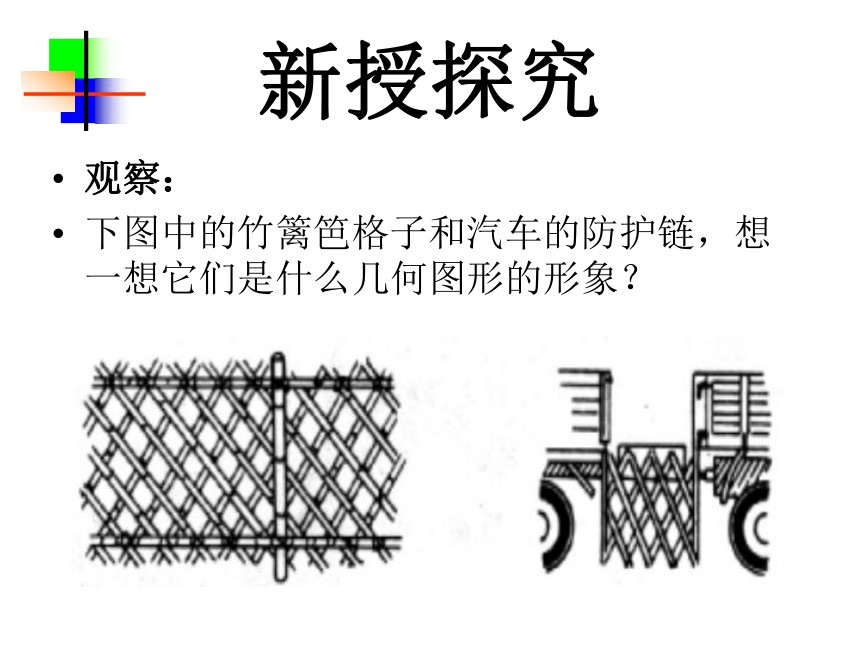
新授探究
观察:
下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
思考:
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
你能总结出平行四边形的定义吗?
平行四边形
1.定义:
A
D
C
B
即:
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形。
定义的双重性
具备“两组对边分别平行”的四边形,才是“平行四边形”,
反过来,“平行四边形”就一定具有“两组对边分别平行”性质。
平行四边形记法:
“ 平行四边形 ” 可用符号“ ”表示。
平行四边形ABCD 记作: ABCD
注意: 图形中字母的标识顺序应为顺时针方向或逆时针方向。
两组对边分别平行的四边形是平行四边形.
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
D
O
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
已知:如图,在平行四边形 ABCD中,
求证:AB=CD,AD=BC,
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ AB=CD,CB=AD,
(作对角线是解决四边形问题常用的辅助线,
通过作对角线,可以把未知问题转化为已知的
关于三角形的问题.)
A
D
C
B
1
4
2
3
已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ ∠B=∠D.
又∵ ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
(作对角线是解决四边形问题常用的辅助线,
通过作对角线,可以把未知问题转化为已知的
关于三角形的问题.)
A
D
C
B
1
4
2
3
已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明: ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠A+ ∠D =180°,
∠A+∠B=180°
∴∠ D=∠ B,
同理:
∠A+ ∠D =180°,
∠C+∠D=180°,
∴∠A= ∠C
A
D
C
B
如图:在 ABCD中,AC与BD相交与点O。
求证:OA=OC OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC OB=OD
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
探讨平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
巩固练习:
如图,在平行四边形ABCD中,AE=CF,
求证:AF=CE.
1.在 ABCD中,∠A= ,则∠B= °,∠D= °
2.如果 ABCD中,∠A+∠C=240°,则∠A= °,
∠B= °.
3.如果 ABCD的周长为28cm,且AB:BC=2∶5,那么
AB= cm,BC= cm,CD= cm,CD= cm.
填空
4.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_______.
O
B
A
C
D
4
60
120
10
4
10
26
130
130
如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
相信自己,你是最棒的!!
课内总结:
今天,你收获了什么?
相信自己,你是最棒的!!
(1)什么样的四边形是平行四边形?
四边形与平行四边形的关系是:
(2)平行四边形的性质:
①具有一般四边形的性质(内角和是360°).
②角:平行四边形的对角相等,邻角互补.
③边:平行四边形的对边平行且相等.
④对角线:对角线互相平分。
小结:
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠BAD=∠BCD,
∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
课后作业
填空:
(1)在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
(2)如果ABCD中,∠A—∠B=240,则∠A= 度,∠B= 度,∠C= 度,∠D= 度.
(3)如果ABCD的周长为28cm,且AB:BC=2∶5,那么AB= cm,BC= cm,CD= cm,CD= cm.
如图4.3-9,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF
第一课时
教学目标:
理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
培养学生发现问题、解决问题的能力及逻辑推理能力.
教学重点:
平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
教学难点:
运用平行四边形的性质进行有关的论证和计算.
知识回顾:
思考:平行线性质、全等三角形的性质及判定和四边形的概念是什么?
一、四边形的概念
1.定义:
在同一平面内,由不在同一直线上的四条线段首尾顺次相接组成的图形,叫做四边形.
这些常见的四边形共有的性质是什么呢?
知识回顾
( 2 ).四边形的边、角关系:
(1).四边形具有不稳定性
A
D
C
B
4
3
2
1
∠BAD+∠ABC+∠BCD+∠CDA
=(∠D+∠1+∠2)+(∠B+∠4+∠3)
=180°×2
=360°
D
C
B
A
8
7
6
5
∠5+∠6+∠7+∠8=180°×4-360°=360°
小结:四边形的内角和与外角和均为360°.
知识回顾
2.四边形的性质
四边形的三边之和大于第四边。
连结AC
知识回顾
一、基本概念
1.定义:由不在同一直线上的三条线段首尾顺次相接组成的图形,叫做三角形
三角形边、角关系;
三角形的有关线段:高、中线、角平分线
三角形具有稳定性
3.三角形的分类
4.三角形全等的性质及判定
三角形
2.性质
角
边
新授探究
观察:
下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
思考:
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
你能总结出平行四边形的定义吗?
平行四边形
1.定义:
A
D
C
B
即:
∵AB//CD,AD//BC
∴四边形ABCD是平行四边形。
定义的双重性
具备“两组对边分别平行”的四边形,才是“平行四边形”,
反过来,“平行四边形”就一定具有“两组对边分别平行”性质。
平行四边形记法:
“ 平行四边形 ” 可用符号“ ”表示。
平行四边形ABCD 记作: ABCD
注意: 图形中字母的标识顺序应为顺时针方向或逆时针方向。
两组对边分别平行的四边形是平行四边形.
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
D
O
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
探讨平行四边形的性质
如图,在方格纸上有A、B、C三点,请画出以这三点为顶点的平行四边形。
通过画图,试写出平行四边形的关于边、角、对角线的结论。
O
D
已知:如图,在平行四边形 ABCD中,
求证:AB=CD,AD=BC,
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ AB=CD,CB=AD,
(作对角线是解决四边形问题常用的辅助线,
通过作对角线,可以把未知问题转化为已知的
关于三角形的问题.)
A
D
C
B
1
4
2
3
已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明:连接AC, ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AC=CA,
∴ △ABC≌△CDA (ASA)
∴ ∠B=∠D.
又∵ ∠1+∠4=∠2+∠3,
∴ ∠BAD=∠BCD.
(作对角线是解决四边形问题常用的辅助线,
通过作对角线,可以把未知问题转化为已知的
关于三角形的问题.)
A
D
C
B
1
4
2
3
已知:如图,在平行四边形 ABCD中,
求证:∠A=∠C, ∠B=∠D
证明: ABCD中
∵ AB∥CD,AD∥BC,
∴ ∠A+ ∠D =180°,
∠A+∠B=180°
∴∠ D=∠ B,
同理:
∠A+ ∠D =180°,
∠C+∠D=180°,
∴∠A= ∠C
A
D
C
B
如图:在 ABCD中,AC与BD相交与点O。
求证:OA=OC OB=OD
1
4
2
3
A
D
C
B
o
证明: ABCD中
∵ AD∥BC,
∴ ∠1=∠3,∠2=∠4.
又 AD=BC,
∴ △BOC≌△DOA(ASA)
∴ OA=OC OB=OD
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
探讨平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠A=∠C,∠B=∠D
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
巩固练习:
如图,在平行四边形ABCD中,AE=CF,
求证:AF=CE.
1.在 ABCD中,∠A= ,则∠B= °,∠D= °
2.如果 ABCD中,∠A+∠C=240°,则∠A= °,
∠B= °.
3.如果 ABCD的周长为28cm,且AB:BC=2∶5,那么
AB= cm,BC= cm,CD= cm,CD= cm.
填空
4.已知O是 ABCD的对角线交点,
AC=10cm,BD=18cm,AD=12cm,
则△BOC的周长是_______.
O
B
A
C
D
4
60
120
10
4
10
26
130
130
如图所示,平行四边形ABCD的对角线相交于O点,且AB≠BC,过O点作OE⊥AC,交BC于E,如果△ABE的周长为b,则平行四边形ABCD的周长是( )
A. b B. 1.5b C. 2b D. 3b
相信自己,你是最棒的!!
课内总结:
今天,你收获了什么?
相信自己,你是最棒的!!
(1)什么样的四边形是平行四边形?
四边形与平行四边形的关系是:
(2)平行四边形的性质:
①具有一般四边形的性质(内角和是360°).
②角:平行四边形的对角相等,邻角互补.
③边:平行四边形的对边平行且相等.
④对角线:对角线互相平分。
小结:
研究对象 研究结果 几何表示法
边 对边
邻边
角 对角
邻角
对角线
平行四边形的性质
A
D
C
B
平行且相等
相等
互补
∠BAD=∠BCD,
∠ABC=∠ADC
AB∥CD,AD∥BC
=
=
∠A+∠B=180°(略)
互相平分
AO=CO , BO=DO
O
B
A
C
D
邻边之和相等
AB+BC=AD+DC
课后作业
填空:
(1)在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
(2)如果ABCD中,∠A—∠B=240,则∠A= 度,∠B= 度,∠C= 度,∠D= 度.
(3)如果ABCD的周长为28cm,且AB:BC=2∶5,那么AB= cm,BC= cm,CD= cm,CD= cm.
如图4.3-9,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF
