第三章第六节 带电粒子在有界匀强磁场中的运动 课件 23张ppt
文档属性
| 名称 | 第三章第六节 带电粒子在有界匀强磁场中的运动 课件 23张ppt | 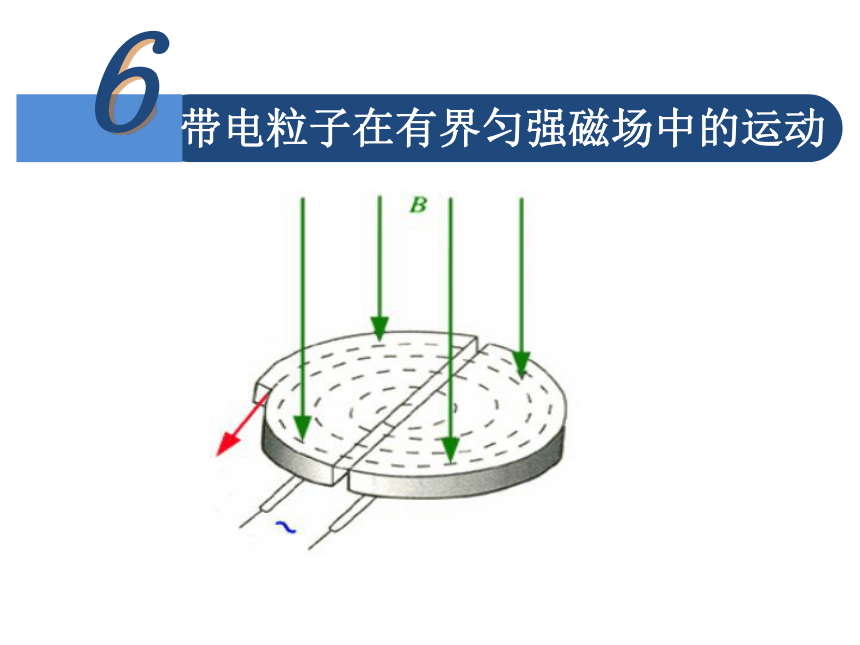 | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 20:58:11 | ||
图片预览


文档简介
(共23张PPT)
6
带电粒子在有界匀强磁场中的运动
B
m,q
v
由洛伦兹力提供向心力:
⑴轨道半径:
⑵运动周期:
⑶动能:
㈠基本规律及物理量
一、带电粒子在匀强磁场中的运动
对于确定磁场,有
,仅由粒子种类决定,与r和v无关
F
O
v0
P
M
v
O
v0
P
M
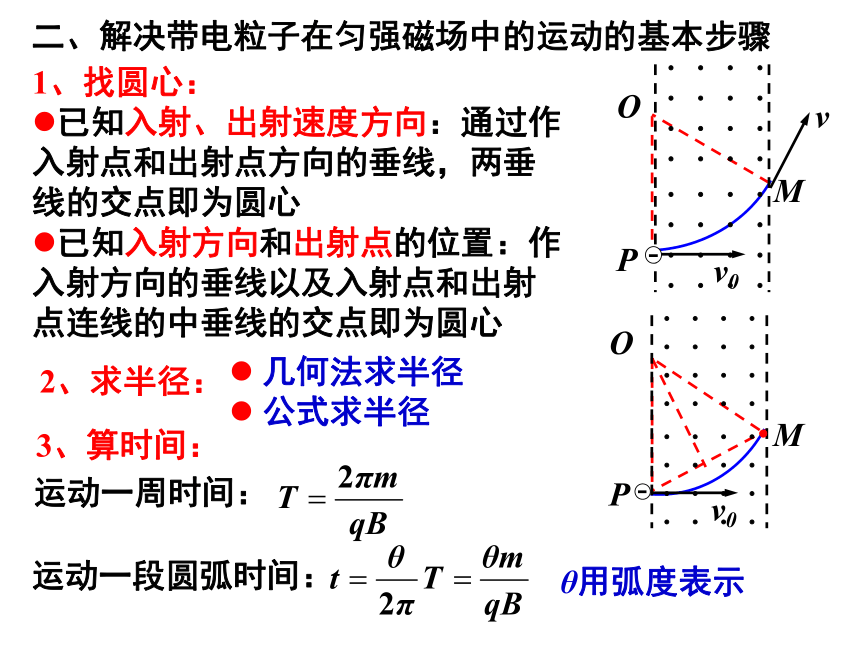
1、找圆心:
已知入射、出射速度方向:通过作入射点和出射点方向的垂线,两垂线的交点即为圆心
已知入射方向和出射点的位置:作入射方向的垂线以及入射点和出射点连线的中垂线的交点即为圆心
2、求半径:
几何法求半径
公式求半径
二、解决带电粒子在匀强磁场中的运动的基本步骤
运动一周时间:
运动一段圆弧时间:
3、算时间:
θ用弧度表示
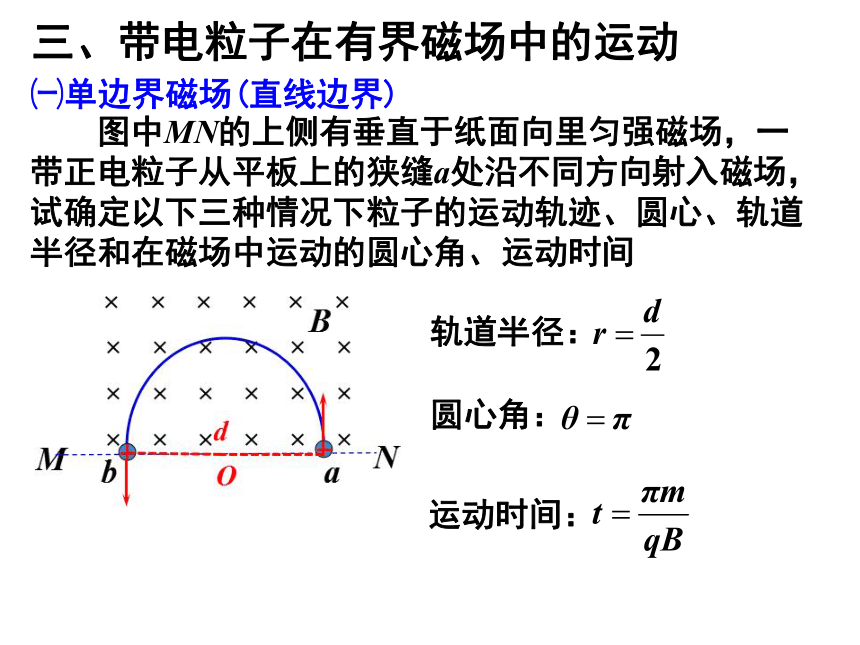
图中MN的上侧有垂直于纸面向里匀强磁场,一带正电粒子从平板上的狭缝a处沿不同方向射入磁场,试确定以下三种情况下粒子的运动轨迹、圆心、轨道半径和在磁场中运动的圆心角、运动时间
㈠单边界磁场(直线边界)
三、带电粒子在有界磁场中的运动
轨道半径:
圆心角:
运动时间:
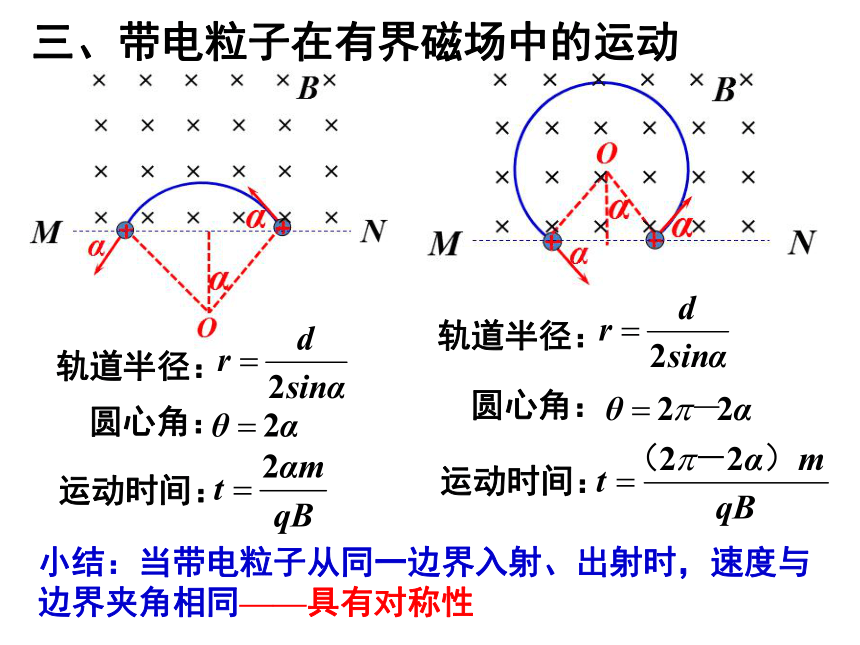
小结:当带电粒子从同一边界入射、出射时,速度与边界夹角相同——具有对称性
三、带电粒子在有界磁场中的运动
轨道半径:
圆心角:
运动时间:
轨道半径:
圆心角:
运动时间:
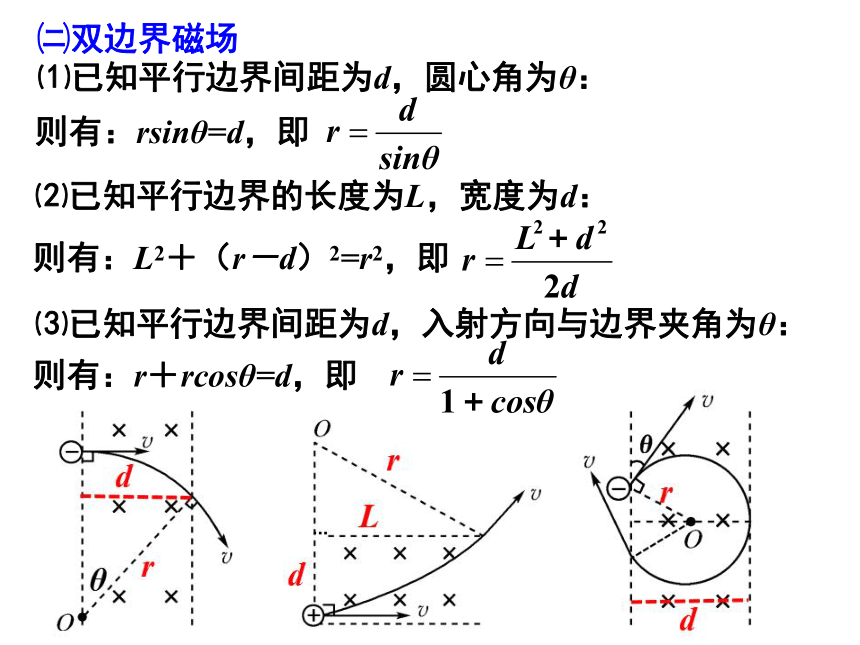
㈡双边界磁场
⑴已知平行边界间距为d,圆心角为θ:
则有:rsinθ=d,即
⑵已知平行边界的长度为L,宽度为d:
则有:L2+(r-d)2=r2,即
⑶已知平行边界间距为d,入射方向与边界夹角为θ:
则有:r+rcosθ=d,即
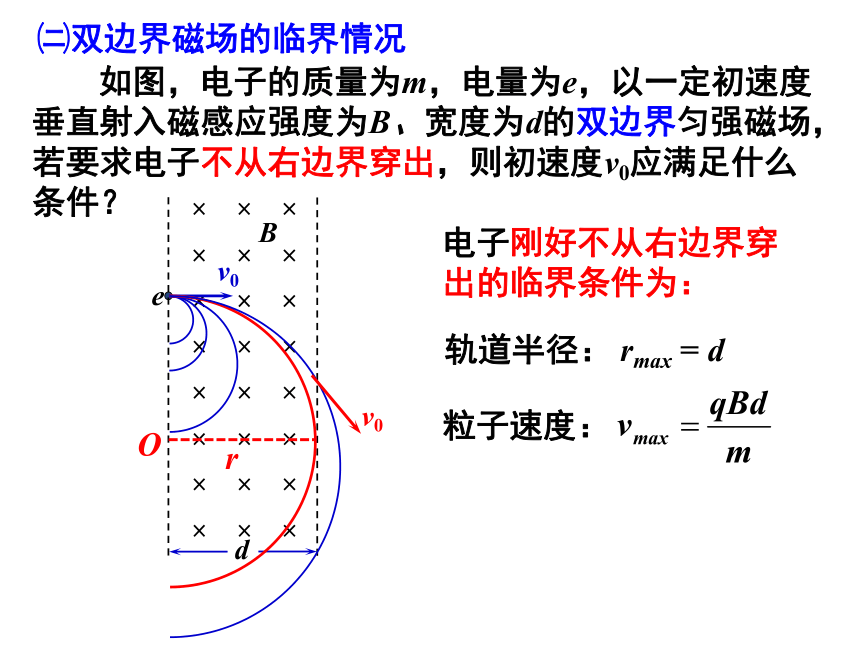
如图,电子的质量为m,电量为e,以一定初速度垂直射入磁感应强度为B、宽度为d的双边界匀强磁场,若要求电子不从右边界穿出,则初速度v0应满足什么条件?
d
e
B
v0
㈡双边界磁场的临界情况
v0
rmax
=
d
轨道半径:
粒子速度:
电子刚好不从右边界穿出的临界条件为:
O
r
d
e
B
v0
d
e
B
v0
r+rcos60?
=
d
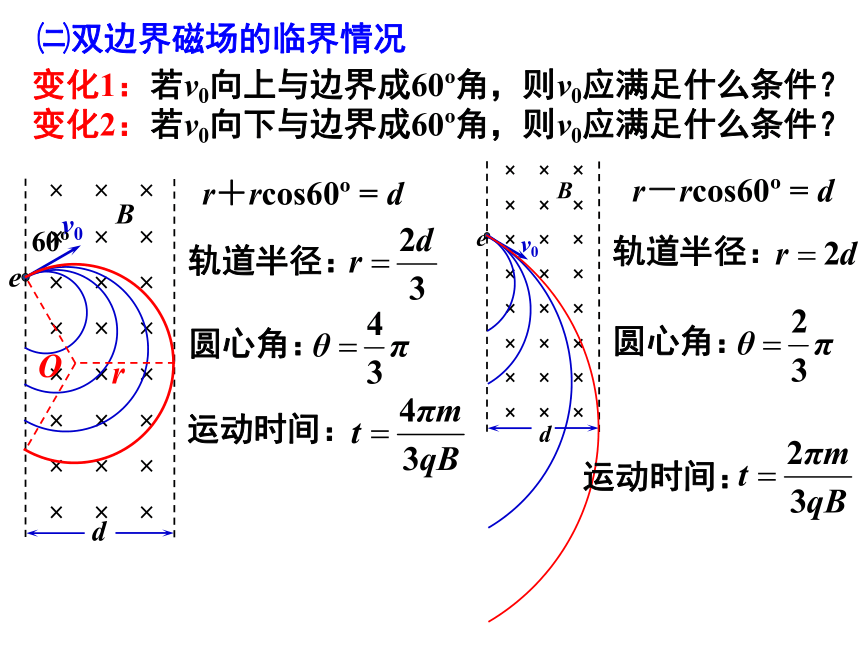
变化1:若v0向上与边界成60?角,则v0应满足什么条件?
变化2:若v0向下与边界成60?角,则v0应满足什么条件?
r-rcos60?
=
d
㈡双边界磁场的临界情况
60?
轨道半径:
圆心角:
运动时间:
轨道半径:
圆心角:
运动时间:
O
r
B
v0
O
边界圆
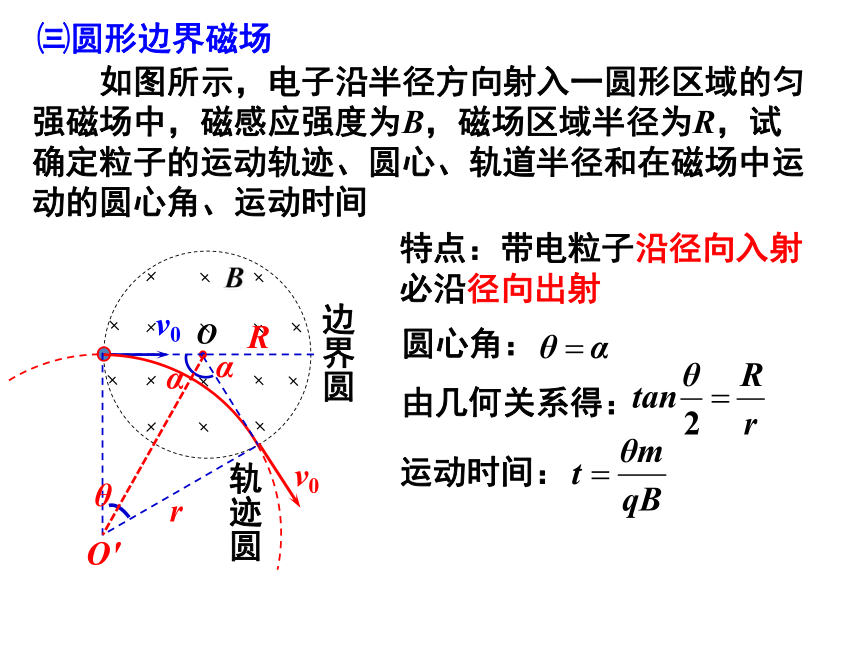
如图所示,电子沿半径方向射入一圆形区域的匀强磁场中,磁感应强度为B,磁场区域半径为R,试确定粒子的运动轨迹、圆心、轨道半径和在磁场中运动的圆心角、运动时间
轨迹圆
O′
α
θ
α
㈢圆形边界磁场
特点:带电粒子沿径向入射必沿径向出射
由几何关系得:
圆心角:
运动时间:
R
r
v0
B
v
O
边界圆
带电粒子在匀强磁场中仅受磁场力作用时做匀速圆周运动,因此,带电粒子在圆形匀强磁场中的运动往往涉及粒子轨迹圆与磁场边界圆的两圆相交问题
两种基本情形:
轨迹圆
O′
α
θ
θ+
α
=π
两圆心连线OO′与点C共线。
B
O
边界圆
轨迹圆
B
C
A
O'
θ
㈢圆形边界磁场
B
v
O
边界圆
轨迹圆
O′
α
θ
θ+
α
=
π
θ
(三)圆形边界磁场
【例4】如图虚线所示区域内有方向垂直于纸面的匀强磁场,一束速度大小各不相同的质子正对该区域的圆心O射入这个磁场;结果,这些质子在该磁场中运动的时间有的较长,有的较短,其中运动时间较长的粒子(
)
A.射入时的速度一定较大
B.在该磁场中运动的路程一定
较长
C.在该磁场中偏转的角度一定较大
D.从该磁场中飞出的速度一定较小
C
D
两圆心连线OO′与点C共线。
轨迹圆
B
C
A
O'
(三)圆形边界磁场
【例5】(2013年新课标Ⅰ卷)
如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外,一电荷量为q(q>0)。质量为m的离子沿平行于ab的直径方向射入磁场区域,射入点与ab的距离为R/2,已知离子射出磁场与射入磁场时运动方向间的夹角为60°,则离子的速率为(不计重力)
A.
B.
C.
D.
√
(一)解决此类问题关键是找准临界点,审题应抓住题目中的“恰好”“最大”“最高”“至少”等词语作为突破口,挖掘隐含条件,分析可能的情况,如有必要则画出几个不同半径相应的轨迹图,从而分析出临界条件.寻找临界点的两种有效方法:
1.轨迹圆的缩放:当粒子的入射方向不变而速度大小可变时,粒子做圆周运动的轨迹圆心一定在入射点所受洛伦兹力所表示的射线上,但位置(半径R)不确定,用圆规作出一系列大小不同的轨迹圆,从圆的动态变化中即可发现“临界点”。
2.轨迹圆的旋转:当粒子的入射速度大小确定而方向不确定时,所有不同方向入射的粒子的轨迹圆是一样大的,只是位置绕入射点发生了旋转,从定圆的动态旋转(作图)中,也容易发现“临界点”。
三、带电粒子在有界磁场中运动的临界极值问题
a
d
c
b
θ
B
①速度较小时粒子做部分圆周运动后从原边界飞出;②速度在某一范围内从上侧面边界飞;③速度较大时粒子做部分圆周运动从右侧面边界飞出;④速度更大时粒子做部分圆周运动从下侧面边界飞出。
【例7】如图所示,一足够长的矩形区域abcd内有磁感应强度为B,方向垂直纸面向里的匀强磁场,现从ad边的中点O处,以垂直磁场且跟ad边成30°角的速度方向射入一带电粒子.已知粒子质量为m,带电荷量为q,ad边长为l,不计粒子重力.求:
(1)若要粒子从ab边上射出,则入射速度v0的范围是多少?
(2)粒子在磁场中运动的最长时间为多少?
圆心在过入射点跟速度方向垂直的直线上
【例8】如图8所示,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光板ab,板面与磁场方向平行,在距ab的距离l=16cm处,有一个点状的α放射源S,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比q/m=5.0×107C/kg,现只考虑在图纸平面中运动的α粒子,求ab上被α粒子打中的区域的长度。
解析:α粒子带正电,故在磁场中沿逆时针方向做匀速圆周运动,用R表示轨道半径,有qvB=mv2/R,
由此得??
R=mv/qB,代入数值得R=10cm。
可见,2R>l>R,如图所示,因朝不同方向发射的α粒子的圆轨迹都过S,由此可知,某一圆轨迹在图中N左侧与ab相切,则此切点P1就是α粒子能打中的左侧最远点。
再考虑N的右侧。任何α粒子在运动中离S的距离不可能超过2R,以2R为半径、S为圆心作圆,交ab于N右侧的P2点,此即右侧能打到的最远点。
由图中几何关系得
所求长度为
P1P2=NP1+NP2,
代入数值得
P1P2=20cm。
四、带电粒子在有界磁场中做匀速圆周运动的多解问题
1.带电粒子电性不确定形成多解
6
带电粒子在有界匀强磁场中的运动
B
m,q
v
由洛伦兹力提供向心力:
⑴轨道半径:
⑵运动周期:
⑶动能:
㈠基本规律及物理量
一、带电粒子在匀强磁场中的运动
对于确定磁场,有
,仅由粒子种类决定,与r和v无关
F
O
v0
P
M
v
O
v0
P
M
1、找圆心:
已知入射、出射速度方向:通过作入射点和出射点方向的垂线,两垂线的交点即为圆心
已知入射方向和出射点的位置:作入射方向的垂线以及入射点和出射点连线的中垂线的交点即为圆心
2、求半径:
几何法求半径
公式求半径
二、解决带电粒子在匀强磁场中的运动的基本步骤
运动一周时间:
运动一段圆弧时间:
3、算时间:
θ用弧度表示
图中MN的上侧有垂直于纸面向里匀强磁场,一带正电粒子从平板上的狭缝a处沿不同方向射入磁场,试确定以下三种情况下粒子的运动轨迹、圆心、轨道半径和在磁场中运动的圆心角、运动时间
㈠单边界磁场(直线边界)
三、带电粒子在有界磁场中的运动
轨道半径:
圆心角:
运动时间:
小结:当带电粒子从同一边界入射、出射时,速度与边界夹角相同——具有对称性
三、带电粒子在有界磁场中的运动
轨道半径:
圆心角:
运动时间:
轨道半径:
圆心角:
运动时间:
㈡双边界磁场
⑴已知平行边界间距为d,圆心角为θ:
则有:rsinθ=d,即
⑵已知平行边界的长度为L,宽度为d:
则有:L2+(r-d)2=r2,即
⑶已知平行边界间距为d,入射方向与边界夹角为θ:
则有:r+rcosθ=d,即
如图,电子的质量为m,电量为e,以一定初速度垂直射入磁感应强度为B、宽度为d的双边界匀强磁场,若要求电子不从右边界穿出,则初速度v0应满足什么条件?
d
e
B
v0
㈡双边界磁场的临界情况
v0
rmax
=
d
轨道半径:
粒子速度:
电子刚好不从右边界穿出的临界条件为:
O
r
d
e
B
v0
d
e
B
v0
r+rcos60?
=
d
变化1:若v0向上与边界成60?角,则v0应满足什么条件?
变化2:若v0向下与边界成60?角,则v0应满足什么条件?
r-rcos60?
=
d
㈡双边界磁场的临界情况
60?
轨道半径:
圆心角:
运动时间:
轨道半径:
圆心角:
运动时间:
O
r
B
v0
O
边界圆
如图所示,电子沿半径方向射入一圆形区域的匀强磁场中,磁感应强度为B,磁场区域半径为R,试确定粒子的运动轨迹、圆心、轨道半径和在磁场中运动的圆心角、运动时间
轨迹圆
O′
α
θ
α
㈢圆形边界磁场
特点:带电粒子沿径向入射必沿径向出射
由几何关系得:
圆心角:
运动时间:
R
r
v0
B
v
O
边界圆
带电粒子在匀强磁场中仅受磁场力作用时做匀速圆周运动,因此,带电粒子在圆形匀强磁场中的运动往往涉及粒子轨迹圆与磁场边界圆的两圆相交问题
两种基本情形:
轨迹圆
O′
α
θ
θ+
α
=π
两圆心连线OO′与点C共线。
B
O
边界圆
轨迹圆
B
C
A
O'
θ
㈢圆形边界磁场
B
v
O
边界圆
轨迹圆
O′
α
θ
θ+
α
=
π
θ
(三)圆形边界磁场
【例4】如图虚线所示区域内有方向垂直于纸面的匀强磁场,一束速度大小各不相同的质子正对该区域的圆心O射入这个磁场;结果,这些质子在该磁场中运动的时间有的较长,有的较短,其中运动时间较长的粒子(
)
A.射入时的速度一定较大
B.在该磁场中运动的路程一定
较长
C.在该磁场中偏转的角度一定较大
D.从该磁场中飞出的速度一定较小
C
D
两圆心连线OO′与点C共线。
轨迹圆
B
C
A
O'
(三)圆形边界磁场
【例5】(2013年新课标Ⅰ卷)
如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外,一电荷量为q(q>0)。质量为m的离子沿平行于ab的直径方向射入磁场区域,射入点与ab的距离为R/2,已知离子射出磁场与射入磁场时运动方向间的夹角为60°,则离子的速率为(不计重力)
A.
B.
C.
D.
√
(一)解决此类问题关键是找准临界点,审题应抓住题目中的“恰好”“最大”“最高”“至少”等词语作为突破口,挖掘隐含条件,分析可能的情况,如有必要则画出几个不同半径相应的轨迹图,从而分析出临界条件.寻找临界点的两种有效方法:
1.轨迹圆的缩放:当粒子的入射方向不变而速度大小可变时,粒子做圆周运动的轨迹圆心一定在入射点所受洛伦兹力所表示的射线上,但位置(半径R)不确定,用圆规作出一系列大小不同的轨迹圆,从圆的动态变化中即可发现“临界点”。
2.轨迹圆的旋转:当粒子的入射速度大小确定而方向不确定时,所有不同方向入射的粒子的轨迹圆是一样大的,只是位置绕入射点发生了旋转,从定圆的动态旋转(作图)中,也容易发现“临界点”。
三、带电粒子在有界磁场中运动的临界极值问题
a
d
c
b
θ
B
①速度较小时粒子做部分圆周运动后从原边界飞出;②速度在某一范围内从上侧面边界飞;③速度较大时粒子做部分圆周运动从右侧面边界飞出;④速度更大时粒子做部分圆周运动从下侧面边界飞出。
【例7】如图所示,一足够长的矩形区域abcd内有磁感应强度为B,方向垂直纸面向里的匀强磁场,现从ad边的中点O处,以垂直磁场且跟ad边成30°角的速度方向射入一带电粒子.已知粒子质量为m,带电荷量为q,ad边长为l,不计粒子重力.求:
(1)若要粒子从ab边上射出,则入射速度v0的范围是多少?
(2)粒子在磁场中运动的最长时间为多少?
圆心在过入射点跟速度方向垂直的直线上
【例8】如图8所示,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T,磁场内有一块平面感光板ab,板面与磁场方向平行,在距ab的距离l=16cm处,有一个点状的α放射源S,它向各个方向发射α粒子,α粒子的速度都是v=3.0×106m/s,已知α粒子的电荷与质量之比q/m=5.0×107C/kg,现只考虑在图纸平面中运动的α粒子,求ab上被α粒子打中的区域的长度。
解析:α粒子带正电,故在磁场中沿逆时针方向做匀速圆周运动,用R表示轨道半径,有qvB=mv2/R,
由此得??
R=mv/qB,代入数值得R=10cm。
可见,2R>l>R,如图所示,因朝不同方向发射的α粒子的圆轨迹都过S,由此可知,某一圆轨迹在图中N左侧与ab相切,则此切点P1就是α粒子能打中的左侧最远点。
再考虑N的右侧。任何α粒子在运动中离S的距离不可能超过2R,以2R为半径、S为圆心作圆,交ab于N右侧的P2点,此即右侧能打到的最远点。
由图中几何关系得
所求长度为
P1P2=NP1+NP2,
代入数值得
P1P2=20cm。
四、带电粒子在有界磁场中做匀速圆周运动的多解问题
1.带电粒子电性不确定形成多解
