5.7生活中的圆周运动 课件 33张PPT
文档属性
| 名称 | 5.7生活中的圆周运动 课件 33张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
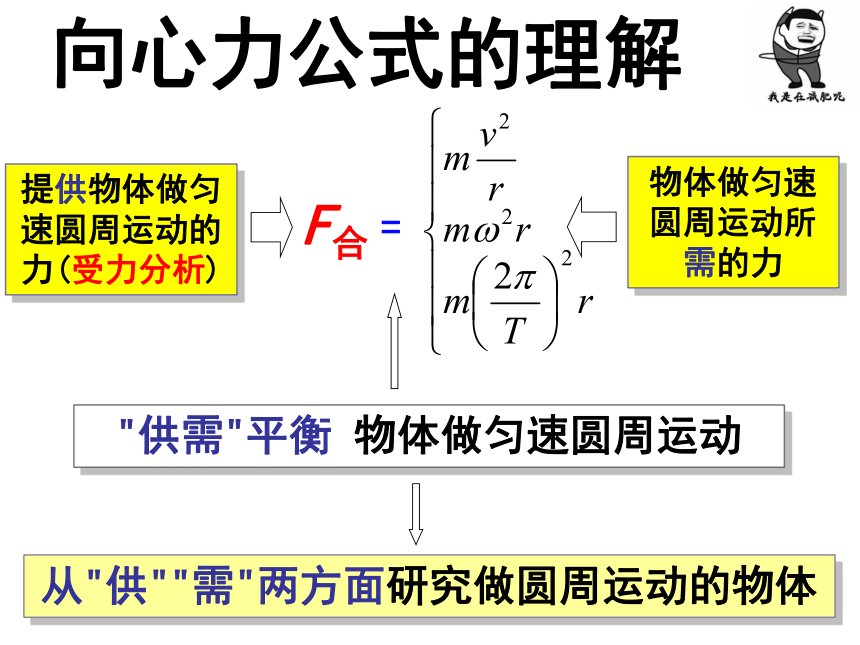
7
生活中的圆周运动
F合
"供需"平衡
物体做匀速圆周运动
提供物体做匀速圆周运动的力(受力分析)
物体做匀速圆周运动所需的力
向心力公式的理解
=
从"供""需"两方面研究做圆周运动的物体
两类圆周运动问题分析
水平面内的圆周运动
竖直面内的圆周运动
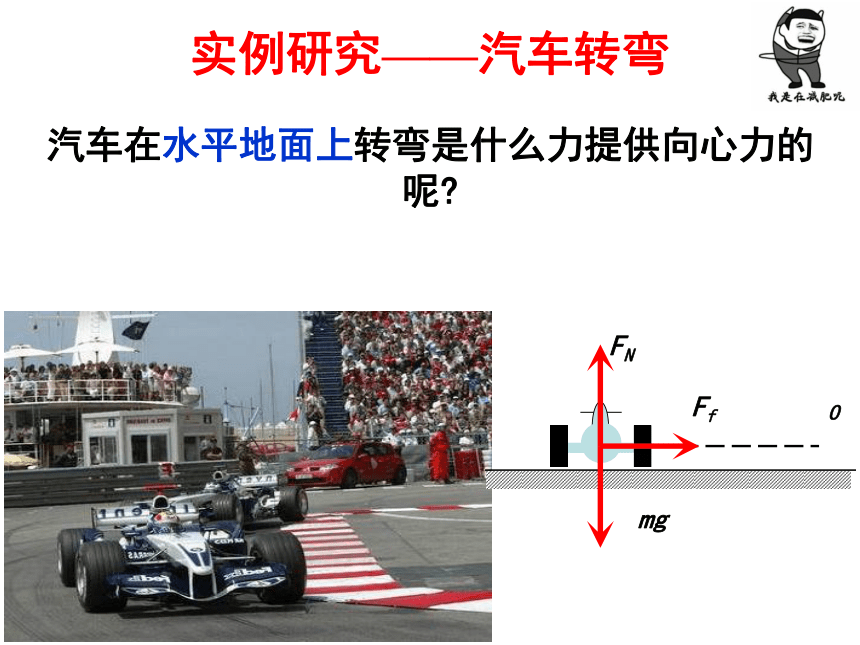
汽车转弯
火车转弯
汽车过桥
汽车在水平地面上转弯是什么力提供向心力的呢?
O
mg
FN
Ff
实例研究——汽车转弯
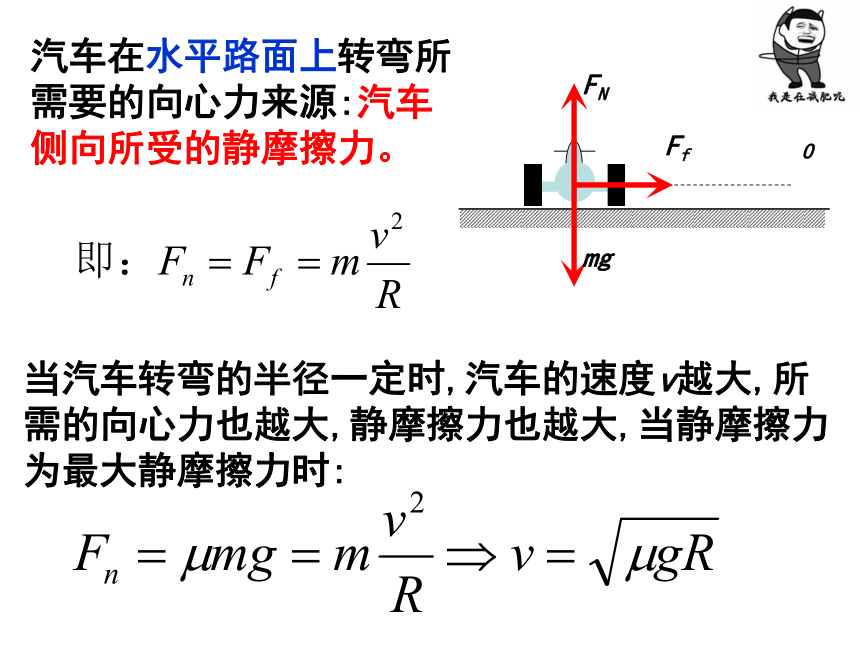
汽车在水平路面上转弯所需要的向心力来源:汽车侧向所受的静摩擦力。
O
mg
FN
Ff
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,当静摩擦力为最大静摩擦力时:
O
mg
FN
Ff
由此可见:汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径;
(2)增加路面的粗糙程度;
(3)增加路面高度差——外高内低;
(4)最重要的一点:司机应该减速慢行!
实例研究——火车转弯
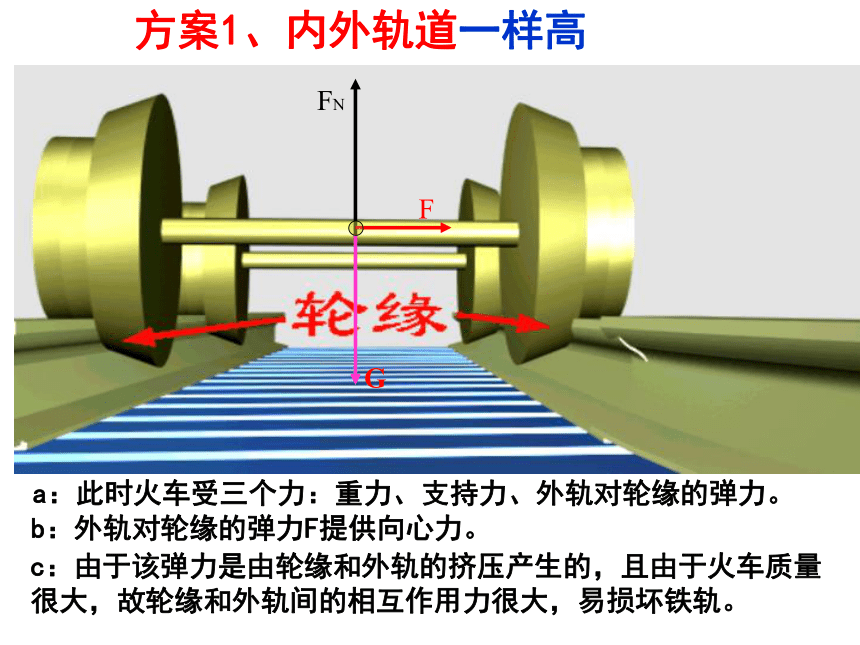
c:由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨。
FN
F
G
a:此时火车受三个力:重力、支持力、外轨对轮缘的弹力。
b:外轨对轮缘的弹力F提供向心力。
方案1、内外轨道一样高
方案2、外轨高内轨低
G
Fn
N
h
L
θ
θ
此为火车转弯时的设计速度
r
如果实际速度太大,
外
内
如果实际速度太小,
轨对轮缘有向外的弹力。
轨对轮缘有向里的弹力;
当把外轨垫高一定高度时:
F弹
F弹
恰好由重力和支持力的合力提供向心力
1、汽车过拱桥(凸形桥)
质量为m
的汽车以恒定的速率v通过半径为r的拱桥,如图所示,求汽车在桥顶时对路面的压力是多大?
实例研究——汽车过桥
汽车在拱桥桥顶:
mg
FN
O
r
供
由牛顿第三定律:
(1)由
可知汽车的速度越大对桥的压力越小。
(2)当
时汽车对桥的压力为零。(临界速度)
(3)当v大于v临界时,汽车将出现飞车现象。
由于加速度a竖直向下,属失重现象。
求
=
=
泸定桥
汽车经过凹形桥:
拓展:质量为m的汽车以恒定的速率v通过半径为r的凹形桥面,如图所示,求汽车在最低点时对桥面的压力是多大?
G
FN
由牛顿第三定律:
F
Ff
由于加速度a的方向竖直向上,属超重现象。
(1)汽车对桥的压力FN?=
FN>
G
(2)汽车的速度越大
汽车对桥的压力越大
供
求
=
=
比较三种桥面受力的情况
FN
=
G
G
FN
G
G
FN
FN
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力为零?这时驾驶员与座椅之间的压力是多少?……
该情景其实已经实现,不过不是在汽车上,而是在航天飞机中.
航天器中的失重现象
航天器中的失重现象
O
因为
mg
–
N
=
mv2
/
R
所以
N
=
mg
-
mv2/R
当
时,
N=0,航天员处于完全失重状态。
汽车在水平地面上转弯时,地面的摩擦力已达到最大,当汽车速率增大为原来的2倍时,则汽车转弯的轨道半径必须( )
A.减小为原来的1/2
B.减小为原来的1/4
C.增大为原来的2倍
D.增大为原来的4倍
铁道转弯处内、外铁轨间设计有高度差,可以使火车顺利转弯,下列说法中正确的是( )
A.主要是为了减少车轮与铁轨间的摩擦
B.主要是为了减少轮缘与铁轨间的挤压
C.内轨应略高于外轨
D.重力和支持力的合力为火车转弯提供了向心力
汽车以恒定的速率通过一圆弧形拱桥,当它位于拱桥顶部时,下列说法正确的是( )
A.汽车处于超重状态
B.汽车对拱桥的压力等于其重力
C.汽车受重力、支持力、牵引力、摩擦力和向心力的作用
D.汽车受到的重力和支持力的合力提供它所需的向心力,方向指向圆弧的圆心
1、定义:做匀速圆周运动的物体,在一定条件下,做逐渐远离圆心的运动,这种运动叫离心运动。
原因:物所需的向心力 随着v的增大而增大,
但提供向心力的合力为静摩擦力
Ff≤Ffmax
当Ffmax
<
时,产生离心现象。
离心运动
o
做匀速圆周运动的物体,由于惯性总有沿切线方向飞去的倾向,在合外力突然消失或者不足以提供圆周运动所需的向心力的情况下,做逐渐远离圆心的离心运动;当合外力大于物体做圆周运动所需的向心力时,物体做离圆心越来越近的向心运动;只有当合外力等于所需的向心力时,物体才可能做匀速圆周运动。
F拉=mω2r
F拉>mω2r
F拉F拉=0
2、合外力与向心力的关系
"供""需"是否平衡决定物体做何种运动
离心抛掷
离心脱水
离心分离
离心甩干
离心运动
3.应用:
4.危害:
离心运动
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需的向心力,离心运动会使它们破裂,酿成事故。
汽车转弯为什么要减速?
讨论
物做近心运动
绳和内轨模型
mg
FN
v
轨道提供支持力,绳子提供拉力。
竖直面内的圆周运动:“绳”模型
竖直面内的圆周运动:“绳”模型
r
o
mg
N
例.杂技节目“水流星”:一根细绳系着盛水子,演员抡起绳子,杯子就做圆周运动,甚至杯子运动到竖直面内的最高点,已经杯口朝下,水也不会从里洒出.试分析保证这一节目成功的条件是什么?
竖直面内的圆周运动:“绳”模型
v
杆和双轨模型
能过最高点的临界条件:
当速度v
>
时,
杆对小球是拉力;
当速度v
<
时,
杆对小球是支持力;
当速度v
=
时,
杆对小球无作用力。
mg
FN
讨论:
FN=0
杆既可以提供拉力,也可以提供支持力。
FN
FN
竖直面内的圆周运动:“杆”模型
竖直面内的圆周运动:“杆”模型
例:如图所示,一质量为m的小球,用长为L的轻杆固定住,使其在竖直面内做圆周运动。(1)小球做什么运动?
(2)若小球通过最高点时,小球恰好不受杆的作用力,则小球在最高点的速度是多少?
(3)小球能在竖直平面内作圆周运动,必须满足的条件是什么?
mg
O
N
(1)变速圆周运动
“轻绳”模型
“轻杆”模型
常见
类型
过最高点的
临界条件
静止时没有支撑力
静止时有支撑力
“绳”与“杆”两种模型比较
绳
杆
圆管
模型图
m的受力情况
最高点A的速度
重力、
绳的拉力
A
O
m
B
L
重力、杆的拉力或支持力
A
O
m
B
R
重力、外管壁的支持力或内管壁的支持力
竖直平面内的变速圆周运动
A
O
m
B
L
练习:用钢管做成半径为R=0.5m的光滑圆环(管径远小于R)竖直放置,一小球(可看作质点,直径略小于管径)质量为m=0.2kg在环内做圆周运动,求:小球通过最高点A时,下列两种情况下球对管壁的作用力。
取g=10m/s2
A的速率为1.0m/s
A的速率为4.0m/s
解:
A
O
m
先求出杆的弹力为0的速率v0
mg=mv02/l
v02=gl=5
v0=2.25
m/s
(1)
v1=1m/s<
v0
球应受到内壁向上的支持力N1,受力如图示:
FN1
mg
得:
FN1
=1.6
N
(2)
v2=4m/s
>
v0
球应受到外壁向下的支持力N2
如图所示:
A
O
m
FN2
mg
得
FN2
=4.4
N
由牛顿第三定律,球对管壁的作用力分别为:(1)对内壁1.6N向下的压力;(2)对外壁4.4N向上的压力。
练习:如图所示,质量为M的电动机始终静止于地面,其飞轮上固定一质量为m的物体,物体距轮轴为r,为使电动机不至于离开地面,其飞轮转动的角速度ω应如何?
r
M
m
ω
解:当小物体转到最高点时,对底座,受到重力Mg和物体对底座的拉力T,为使电动机不至于离开地面,必须
T≤Mg;对物体,受到重力mg和底座对物体的拉力T。
M
ω
Mg
T
m
mg
T
由圆周运动规律有:mg+T
=
mω2r
即
mω2r≤(M+m)g
7
生活中的圆周运动
F合
"供需"平衡
物体做匀速圆周运动
提供物体做匀速圆周运动的力(受力分析)
物体做匀速圆周运动所需的力
向心力公式的理解
=
从"供""需"两方面研究做圆周运动的物体
两类圆周运动问题分析
水平面内的圆周运动
竖直面内的圆周运动
汽车转弯
火车转弯
汽车过桥
汽车在水平地面上转弯是什么力提供向心力的呢?
O
mg
FN
Ff
实例研究——汽车转弯
汽车在水平路面上转弯所需要的向心力来源:汽车侧向所受的静摩擦力。
O
mg
FN
Ff
当汽车转弯的半径一定时,汽车的速度v越大,所需的向心力也越大,静摩擦力也越大,当静摩擦力为最大静摩擦力时:
O
mg
FN
Ff
由此可见:汽车转弯时,存在一个安全通过的最大速度,如果超过了这个速度,汽车将发生侧滑现象。
改进措施:
(1)增大转弯半径;
(2)增加路面的粗糙程度;
(3)增加路面高度差——外高内低;
(4)最重要的一点:司机应该减速慢行!
实例研究——火车转弯
c:由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨。
FN
F
G
a:此时火车受三个力:重力、支持力、外轨对轮缘的弹力。
b:外轨对轮缘的弹力F提供向心力。
方案1、内外轨道一样高
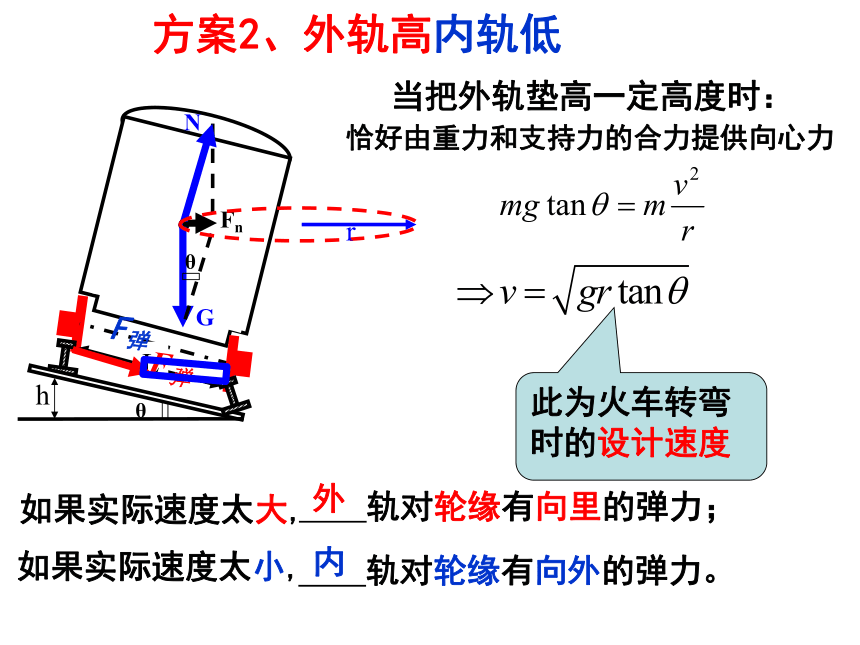
方案2、外轨高内轨低
G
Fn
N
h
L
θ
θ
此为火车转弯时的设计速度
r
如果实际速度太大,
外
内
如果实际速度太小,
轨对轮缘有向外的弹力。
轨对轮缘有向里的弹力;
当把外轨垫高一定高度时:
F弹
F弹
恰好由重力和支持力的合力提供向心力
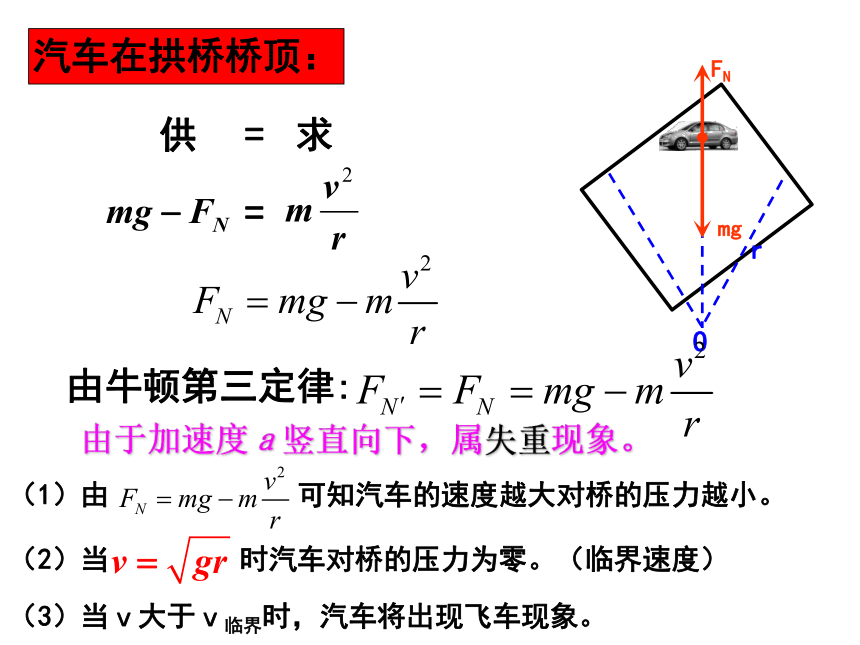
1、汽车过拱桥(凸形桥)
质量为m
的汽车以恒定的速率v通过半径为r的拱桥,如图所示,求汽车在桥顶时对路面的压力是多大?
实例研究——汽车过桥
汽车在拱桥桥顶:
mg
FN
O
r
供
由牛顿第三定律:
(1)由
可知汽车的速度越大对桥的压力越小。
(2)当
时汽车对桥的压力为零。(临界速度)
(3)当v大于v临界时,汽车将出现飞车现象。
由于加速度a竖直向下,属失重现象。
求
=
=
泸定桥
汽车经过凹形桥:
拓展:质量为m的汽车以恒定的速率v通过半径为r的凹形桥面,如图所示,求汽车在最低点时对桥面的压力是多大?
G
FN
由牛顿第三定律:
F
Ff
由于加速度a的方向竖直向上,属超重现象。
(1)汽车对桥的压力FN?=
FN>
G
(2)汽车的速度越大
汽车对桥的压力越大
供
求
=
=
比较三种桥面受力的情况
FN
=
G
G
FN
G
G
FN
FN
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力为零?这时驾驶员与座椅之间的压力是多少?……
该情景其实已经实现,不过不是在汽车上,而是在航天飞机中.
航天器中的失重现象
航天器中的失重现象
O
因为
mg
–
N
=
mv2
/
R
所以
N
=
mg
-
mv2/R
当
时,
N=0,航天员处于完全失重状态。
汽车在水平地面上转弯时,地面的摩擦力已达到最大,当汽车速率增大为原来的2倍时,则汽车转弯的轨道半径必须( )
A.减小为原来的1/2
B.减小为原来的1/4
C.增大为原来的2倍
D.增大为原来的4倍
铁道转弯处内、外铁轨间设计有高度差,可以使火车顺利转弯,下列说法中正确的是( )
A.主要是为了减少车轮与铁轨间的摩擦
B.主要是为了减少轮缘与铁轨间的挤压
C.内轨应略高于外轨
D.重力和支持力的合力为火车转弯提供了向心力
汽车以恒定的速率通过一圆弧形拱桥,当它位于拱桥顶部时,下列说法正确的是( )
A.汽车处于超重状态
B.汽车对拱桥的压力等于其重力
C.汽车受重力、支持力、牵引力、摩擦力和向心力的作用
D.汽车受到的重力和支持力的合力提供它所需的向心力,方向指向圆弧的圆心
1、定义:做匀速圆周运动的物体,在一定条件下,做逐渐远离圆心的运动,这种运动叫离心运动。
原因:物所需的向心力 随着v的增大而增大,
但提供向心力的合力为静摩擦力
Ff≤Ffmax
当Ffmax
<
时,产生离心现象。
离心运动
o
做匀速圆周运动的物体,由于惯性总有沿切线方向飞去的倾向,在合外力突然消失或者不足以提供圆周运动所需的向心力的情况下,做逐渐远离圆心的离心运动;当合外力大于物体做圆周运动所需的向心力时,物体做离圆心越来越近的向心运动;只有当合外力等于所需的向心力时,物体才可能做匀速圆周运动。
F拉=mω2r
F拉>mω2r
F拉
2、合外力与向心力的关系
"供""需"是否平衡决定物体做何种运动
离心抛掷
离心脱水
离心分离
离心甩干
离心运动
3.应用:
4.危害:
离心运动
高速转动的砂轮、飞轮等,都不得超过允许的最大转速。转速过高时,砂轮、飞轮内部分子间的相互作用力不足以提供所需的向心力,离心运动会使它们破裂,酿成事故。
汽车转弯为什么要减速?
讨论
物做近心运动
绳和内轨模型
mg
FN
v
轨道提供支持力,绳子提供拉力。
竖直面内的圆周运动:“绳”模型
竖直面内的圆周运动:“绳”模型
r
o
mg
N
例.杂技节目“水流星”:一根细绳系着盛水子,演员抡起绳子,杯子就做圆周运动,甚至杯子运动到竖直面内的最高点,已经杯口朝下,水也不会从里洒出.试分析保证这一节目成功的条件是什么?
竖直面内的圆周运动:“绳”模型
v
杆和双轨模型
能过最高点的临界条件:
当速度v
>
时,
杆对小球是拉力;
当速度v
<
时,
杆对小球是支持力;
当速度v
=
时,
杆对小球无作用力。
mg
FN
讨论:
FN=0
杆既可以提供拉力,也可以提供支持力。
FN
FN
竖直面内的圆周运动:“杆”模型
竖直面内的圆周运动:“杆”模型
例:如图所示,一质量为m的小球,用长为L的轻杆固定住,使其在竖直面内做圆周运动。(1)小球做什么运动?
(2)若小球通过最高点时,小球恰好不受杆的作用力,则小球在最高点的速度是多少?
(3)小球能在竖直平面内作圆周运动,必须满足的条件是什么?
mg
O
N
(1)变速圆周运动
“轻绳”模型
“轻杆”模型
常见
类型
过最高点的
临界条件
静止时没有支撑力
静止时有支撑力
“绳”与“杆”两种模型比较
绳
杆
圆管
模型图
m的受力情况
最高点A的速度
重力、
绳的拉力
A
O
m
B
L
重力、杆的拉力或支持力
A
O
m
B
R
重力、外管壁的支持力或内管壁的支持力
竖直平面内的变速圆周运动
A
O
m
B
L
练习:用钢管做成半径为R=0.5m的光滑圆环(管径远小于R)竖直放置,一小球(可看作质点,直径略小于管径)质量为m=0.2kg在环内做圆周运动,求:小球通过最高点A时,下列两种情况下球对管壁的作用力。
取g=10m/s2
A的速率为1.0m/s
A的速率为4.0m/s
解:
A
O
m
先求出杆的弹力为0的速率v0
mg=mv02/l
v02=gl=5
v0=2.25
m/s
(1)
v1=1m/s<
v0
球应受到内壁向上的支持力N1,受力如图示:
FN1
mg
得:
FN1
=1.6
N
(2)
v2=4m/s
>
v0
球应受到外壁向下的支持力N2
如图所示:
A
O
m
FN2
mg
得
FN2
=4.4
N
由牛顿第三定律,球对管壁的作用力分别为:(1)对内壁1.6N向下的压力;(2)对外壁4.4N向上的压力。
练习:如图所示,质量为M的电动机始终静止于地面,其飞轮上固定一质量为m的物体,物体距轮轴为r,为使电动机不至于离开地面,其飞轮转动的角速度ω应如何?
r
M
m
ω
解:当小物体转到最高点时,对底座,受到重力Mg和物体对底座的拉力T,为使电动机不至于离开地面,必须
T≤Mg;对物体,受到重力mg和底座对物体的拉力T。
M
ω
Mg
T
m
mg
T
由圆周运动规律有:mg+T
=
mω2r
即
mω2r≤(M+m)g
