物理选修3-3人教版8.1气体的等温变化(共39张ppt)
文档属性
| 名称 | 物理选修3-3人教版8.1气体的等温变化(共39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
第八章
气体
第一节
气体的等温变化
乒乓球内的气体受热,温度升高,压强增大,
体积变大。
车胎内的气体温度升高,压强增大,体积膨胀。
一
问题的引入
问题1
夏天给自行车车胎打气,应注意什么?为什么?
问题2
有什么简便的方法将瘪了的乒乓球恢复原状?这样做的原因?
问题3
以上实例说明描述气体的那几个状态参量存在一定的关系?
1、描述气体的三个状态参量
压强(
p
)
体积(V)
温度(
T
)
(力学性质)
(几何性质)
(热学性质)
2
、控制变量法
二、等温变化(
m不变;T不变)
猜想:
温度不变时,气体的压强和体积之间有什么关系?
一定质量的气体,在温度不变的条件下其压强与体积变化时的关系。我们把这种变化叫做等温变化。
三、实验探究
注射器下端的开口有橡胶套,它和柱塞一起把一段空气柱封闭在玻璃管中。这段空气柱是我们研究的对象,实验过程中它的质量不会变化;
实验中如果空气柱体积的变化不太快,它的温度大致等于环境温度,也不会有明显的变化。
我们的研究对象是什么?
怎样保证气体质量不变?
怎样保证实验过程温度不变?
实验需要测量的物理量?
注射器内一定质量的气体.
压强、体积
变化过程十分缓慢
容器透热
环境恒温
柱塞上涂上润滑油
三、实验探究
实验数据的处理
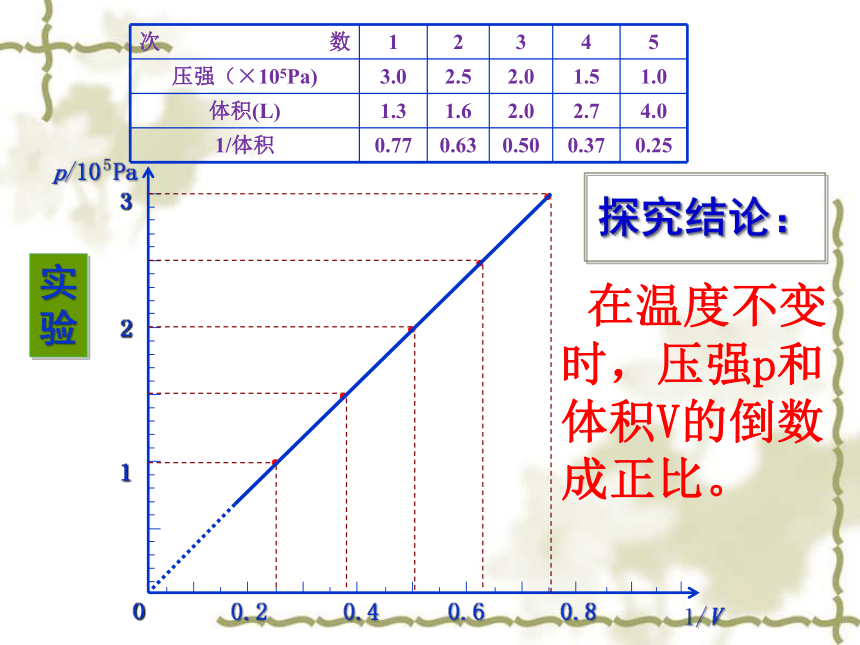
实验
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
p/10
Pa
5
1/V
1
2
3
0
0.2
0.4
0.6
0.8
实验
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
1/体积
0.77
0.63
0.50
0.37
0.25
探究结论:
在温度不变时,压强p和体积V的倒数成正比。
p/10
Pa
5
V
1
2
3
0
1
2
3
4
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
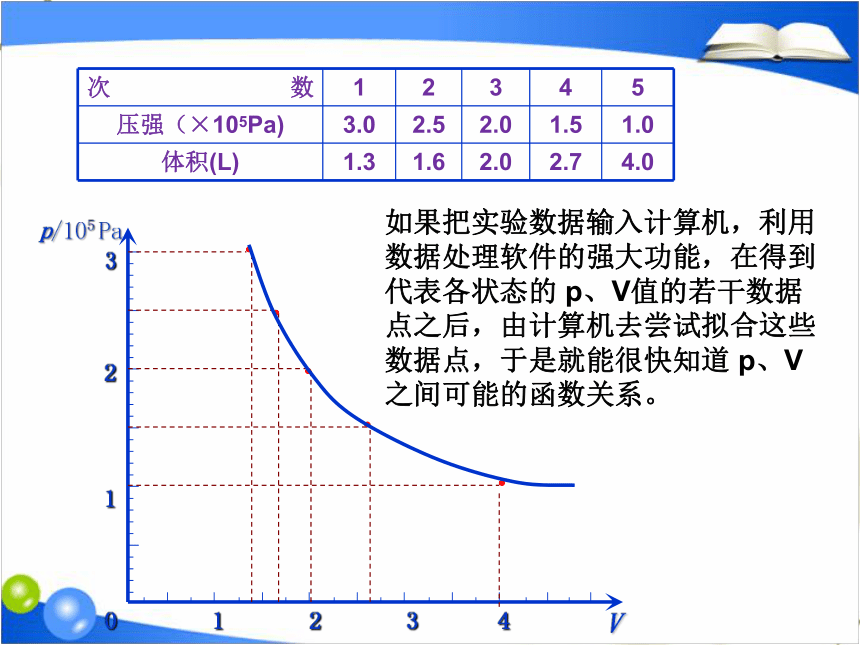
如果把实验数据输入计算机,利用数据处理软件的强大功能,在得到代表各状态的
p、V值的若干数据点之后,由计算机去尝试拟合这些数据点,于是就能很快知道
p、V之间可能的函数关系。
一定质量的某种气体,在温度不变的情
况下,压强P跟体积V成反比
四、玻意耳定律
1、内容:
2、表达式:
研究对象:一定质量的气体
适用条件:温度保持不变化
适用范围:温度不太低,压强不太大
玻意耳—马略特
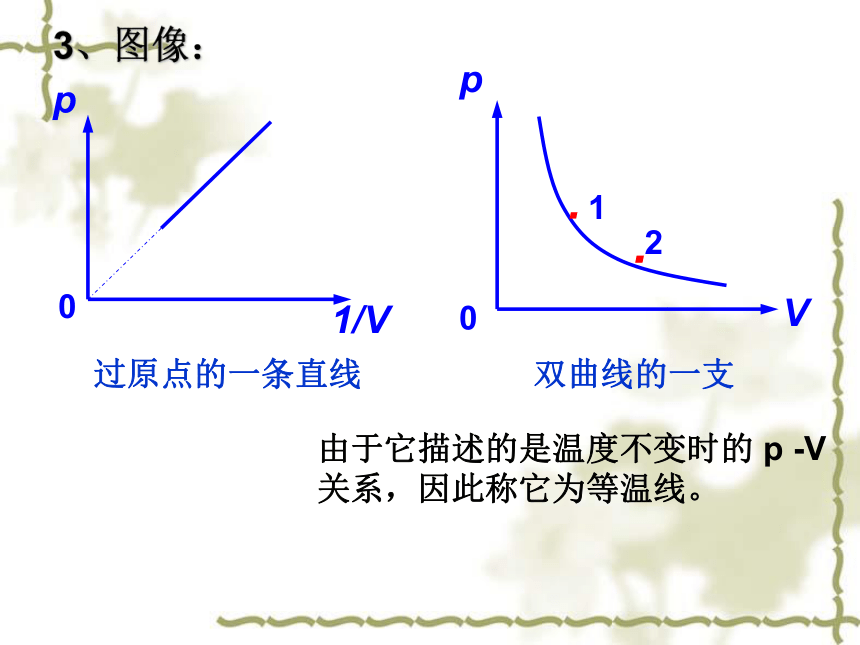
3、图像:
p
1/V
0
过原点的一条直线
V
p
·
0
1
·
2
双曲线的一支
由于它描述的是温度不变时的
p
-V关系,因此称它为等温线。
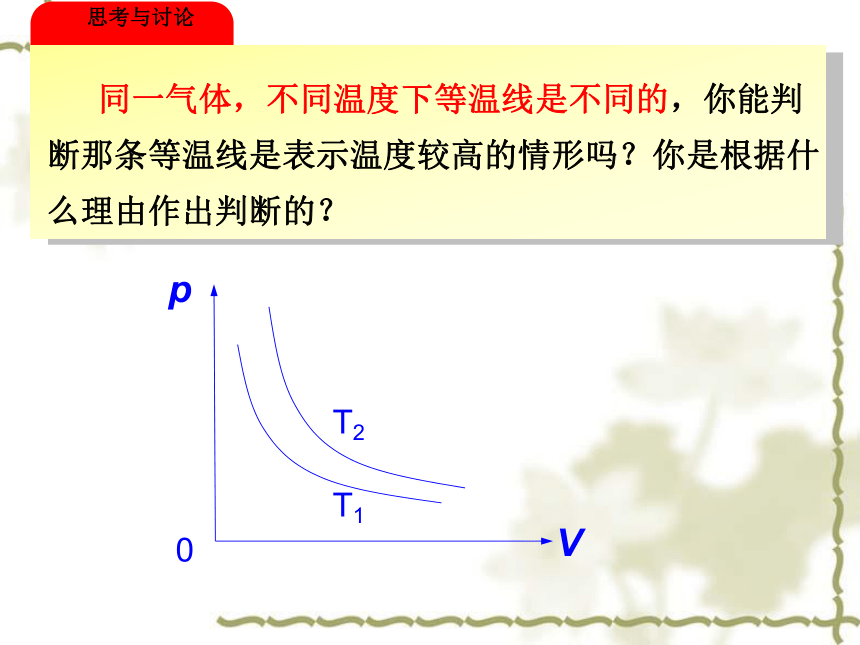
思考与讨论
同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
V
p
T1
T2
0
1.
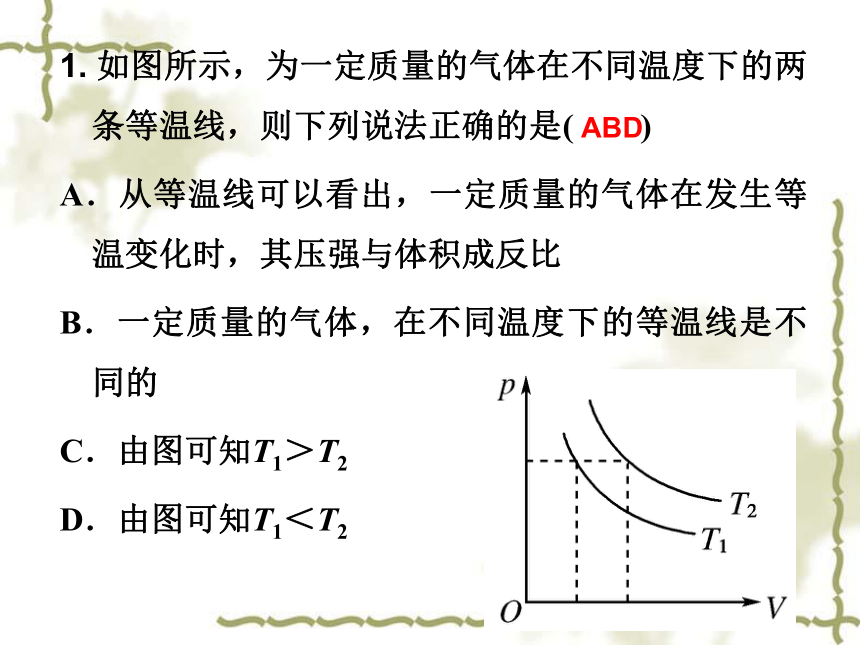
如图所示,为一定质量的气体在不同温度下的两条等温线,则下列说法正确的是( )
A.从等温线可以看出,一定质量的气体在发生等温变化时,其压强与体积成反比
B.一定质量的气体,在不同温度下的等温线是不同的
C.由图可知T1>T2
D.由图可知T1<T2
ABD
2.一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。
答案:
1.25×10
5Pa
利用玻意耳定律解题的基本思路
(1)明确研究对象;
(2)分析过程特点,判断为等温过程;
(3)列出初、末状态的p、V值;
(4)根据p1V1=p2V2列式求解;
(5)讨论结果。
3.汽车轮胎的容积是2.5×10-2m3,轮胎原有1.0×105Pa的空气.向轮胎内缓慢打气,直至压强增加到8.0×105Pa为止,若此过程中温度不变,应向轮胎里打进多大体积1.0×105Pa的空气?
一个篮球的容积是2.5L,用打气筒给这个足球打气,每打一次都把体积为125mL、压强与大气压强相同的空气打进去,如果足球在打气前就已是球形,内部空气压强与大气压相同,那么打了20次以后,足球内部空气的压强是大气压的多少倍?
就篮球而言,外面的气体打到球里,似乎是变质量问题,但是若我们把“球里和球外的气体”作为研究对象,那么质量就不变了。
解:设大气压强为p0,选取球内原来的气体和20次打进的气体的整体为研究对象,
初态:
P1=
P0
V1=(2.5+20×0.125)L,
末态:
P2=?
V2=2.5L
根据玻意耳定律:
???P1V1=P2V2???????????????可解得:P2=2P0??????????????
你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
h
1
h
下列各图装置均处于静止状态。设大气压强为P0,用水银封闭一定量的气体在玻璃管中,求封闭气体的压强P
P
=ρgh
P
=?
cmHg(柱)
P—帕
h—米
P
=P0+ρgh
P
=P0-
ρgh
②
当压强单位取帕斯卡(帕)时
当压强单位取cmHg时
P
=P0+h
P
=P0-
h
一、平衡态下液体封闭气体压强的计算
h
③
P
=P0
1atm
=1.0×105
Pa
=
76cmHg
h
④
h
⑤
h
⑥
连通器原理:同种液体在同一水平面上的压强相等
P
=P0+ρgh
P
=P0-
ρgh
P
=P0-
ρgh
2.
水银气压计中混入了一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768
mm
高的水银柱产生的压强时,这个水银气压计的读数只有
750
mm,此时管中的水银面到管顶的距离为
80
mm。当这个气压计的读数为740
mm水银柱时,实际的大气压相当于多高水银柱产生的压强?设温度保持不变。
二、平衡态下活塞、气缸密闭气体压强的计算
求用活塞封闭在静止容器内的气体压强,应对活塞进行受力分析。然后根据平衡条件求解。
S
m
⑧
m
S
⑦
练习:
气体对面的压力与面垂直:
F=PS
G
P0S
PS
PS
=
P0S+mg
G
PS
P0S′
N
S′
PS
=mg
+P0S'cosθ
PS
=
mg+P0S
M
m
S
⑨
M
m
S
⑩
以活塞为研究对象
以气缸为研究对象
mg+PS
=
P0S
Mg+PS
=
P0S
例2、如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住了一定质量的空气,而活塞与缸套间无摩擦,活塞面积为S,大气压强为P0,则下列说法正确的是(
)
A、内外空气对缸套的总作用力方向向上,大小为Mg
B、内外空气对缸套的总作用力方向向下,大小为mg
C、气缸内空气压强为P0-Mg/S
D、气缸内空气压强为P0+mg/S
AC
1.产生原因――碰撞
大量的气体对器壁的频繁撞击,产生一个均匀的,持续的压力(举例:雨伞),这个压力就产生了压强。
2.说明:压强与深度无关,在各处都相
等,向各个方向都有压强
3.单位:Pa
容器内气体压强
1
Pa=1
N/m2
求封闭气体的压强:
例1
方法总结:取研究对象
受力分析
列平衡式
求出气体压强
其实,生活中许多现象都表明,气体的压强,体积,温度三个状态量之间一定存在某种关系?究竟是什么关系呢?我们怎么来研究?
研究的方法-----控制变量法
本节课我们就来研究控制一定质量的某种气体,温度不变的情况下,压强与体积的变化关系。我们称之为等温变化
玻意耳定律:
一定质量的某种气体在温度不变的情况下,压强跟体积成反比.即pV=C(常量)或
p1V1=p2V2。
(1)成立条件:质量一定,温度不变,且压强不太大,温度不太低。
(2)pV=C。其中常量C?与气体的质量、温度有关。
p
V
0
气体等温变化的p-v图像
t1
t2
压强
(×105Pa)
0.3
0.6
0.9
1.2
1.5
体积
(h0×S)
16
8
5.3
4
3.2
图像:
o
p
P
O
V
(1)一定质量的某种气体在等温变化过程中压强p跟体积V的反比关系,在p-V
直角坐标系中表示出来的图线叫等温线。
等温线
P
O
V
(3)等温线的物理意义:图线上的一点表示气体的一个确定的状态。同一条等温线上各状态的温度相同,p与V
的乘积相同。不同温度下的等温线,离原点越远,温度越高。
(2)一定质量的气体等温线的p-V图是双曲线的一支。
一定质量气体的体积是5ml时,压强为1000Pa。当气体的体积减小3mL时,压强为多大?
前提是打气过程中温度保持不变,实际大气过程中,气体的温度升高
课后练习一:
某容器的容积是5L。里面所装的气体压强为1×106
Pa,温度不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?
课后变式1
课后练习二:
课后变式2
如图所示
水银柱的长度为19cm
大气压为1×10^5pa
相当于76cm高的水银柱产生的压强,玻璃管是粗细均匀的
玻璃管开口向上竖直放置时
被封闭的气柱长15cm
当开口竖直向下放置时水银没有溢出管口被封闭的气柱长度为多少?
容器内装有10×105Pa的气体5kg,
当放出一部分气体后,
容器内的气体压强减小到2×105Pa,
求容器中剩余气体的质量.
(设温度不变)
某种气体在状态A时的压强为2×105Pa体积为1m3,温度为200K。
(1)它经等温过程由状态A变为状态B,体积变为2m3。求状态B的压强。
(2)若经等容过程由状态B变为状态C,温度变为300K,求状态C的压强。
谢
谢
大
家
!
第八章
气体
第一节
气体的等温变化
乒乓球内的气体受热,温度升高,压强增大,
体积变大。
车胎内的气体温度升高,压强增大,体积膨胀。
一
问题的引入
问题1
夏天给自行车车胎打气,应注意什么?为什么?
问题2
有什么简便的方法将瘪了的乒乓球恢复原状?这样做的原因?
问题3
以上实例说明描述气体的那几个状态参量存在一定的关系?
1、描述气体的三个状态参量
压强(
p
)
体积(V)
温度(
T
)
(力学性质)
(几何性质)
(热学性质)
2
、控制变量法
二、等温变化(
m不变;T不变)
猜想:
温度不变时,气体的压强和体积之间有什么关系?
一定质量的气体,在温度不变的条件下其压强与体积变化时的关系。我们把这种变化叫做等温变化。
三、实验探究
注射器下端的开口有橡胶套,它和柱塞一起把一段空气柱封闭在玻璃管中。这段空气柱是我们研究的对象,实验过程中它的质量不会变化;
实验中如果空气柱体积的变化不太快,它的温度大致等于环境温度,也不会有明显的变化。
我们的研究对象是什么?
怎样保证气体质量不变?
怎样保证实验过程温度不变?
实验需要测量的物理量?
注射器内一定质量的气体.
压强、体积
变化过程十分缓慢
容器透热
环境恒温
柱塞上涂上润滑油
三、实验探究
实验数据的处理
实验
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
p/10
Pa
5
1/V
1
2
3
0
0.2
0.4
0.6
0.8
实验
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
1/体积
0.77
0.63
0.50
0.37
0.25
探究结论:
在温度不变时,压强p和体积V的倒数成正比。
p/10
Pa
5
V
1
2
3
0
1
2
3
4
次数
1
2
3
4
5
压强(×105Pa)
3.0
2.5
2.0
1.5
1.0
体积(L)
1.3
1.6
2.0
2.7
4.0
如果把实验数据输入计算机,利用数据处理软件的强大功能,在得到代表各状态的
p、V值的若干数据点之后,由计算机去尝试拟合这些数据点,于是就能很快知道
p、V之间可能的函数关系。
一定质量的某种气体,在温度不变的情
况下,压强P跟体积V成反比
四、玻意耳定律
1、内容:
2、表达式:
研究对象:一定质量的气体
适用条件:温度保持不变化
适用范围:温度不太低,压强不太大
玻意耳—马略特
3、图像:
p
1/V
0
过原点的一条直线
V
p
·
0
1
·
2
双曲线的一支
由于它描述的是温度不变时的
p
-V关系,因此称它为等温线。
思考与讨论
同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
V
p
T1
T2
0
1.
如图所示,为一定质量的气体在不同温度下的两条等温线,则下列说法正确的是( )
A.从等温线可以看出,一定质量的气体在发生等温变化时,其压强与体积成反比
B.一定质量的气体,在不同温度下的等温线是不同的
C.由图可知T1>T2
D.由图可知T1<T2
ABD
2.一定质量气体的体积是20L时,压强为1×105Pa。当气体的体积减小到16L时,压强为多大?设气体的温度保持不变。
答案:
1.25×10
5Pa
利用玻意耳定律解题的基本思路
(1)明确研究对象;
(2)分析过程特点,判断为等温过程;
(3)列出初、末状态的p、V值;
(4)根据p1V1=p2V2列式求解;
(5)讨论结果。
3.汽车轮胎的容积是2.5×10-2m3,轮胎原有1.0×105Pa的空气.向轮胎内缓慢打气,直至压强增加到8.0×105Pa为止,若此过程中温度不变,应向轮胎里打进多大体积1.0×105Pa的空气?
一个篮球的容积是2.5L,用打气筒给这个足球打气,每打一次都把体积为125mL、压强与大气压强相同的空气打进去,如果足球在打气前就已是球形,内部空气压强与大气压相同,那么打了20次以后,足球内部空气的压强是大气压的多少倍?
就篮球而言,外面的气体打到球里,似乎是变质量问题,但是若我们把“球里和球外的气体”作为研究对象,那么质量就不变了。
解:设大气压强为p0,选取球内原来的气体和20次打进的气体的整体为研究对象,
初态:
P1=
P0
V1=(2.5+20×0.125)L,
末态:
P2=?
V2=2.5L
根据玻意耳定律:
???P1V1=P2V2???????????????可解得:P2=2P0??????????????
你在得出结论时考虑到了什么前提?实际打气时的情况能够满足你的前提吗?
h
1
h
下列各图装置均处于静止状态。设大气压强为P0,用水银封闭一定量的气体在玻璃管中,求封闭气体的压强P
P
=ρgh
P
=?
cmHg(柱)
P—帕
h—米
P
=P0+ρgh
P
=P0-
ρgh
②
当压强单位取帕斯卡(帕)时
当压强单位取cmHg时
P
=P0+h
P
=P0-
h
一、平衡态下液体封闭气体压强的计算
h
③
P
=P0
1atm
=1.0×105
Pa
=
76cmHg
h
④
h
⑤
h
⑥
连通器原理:同种液体在同一水平面上的压强相等
P
=P0+ρgh
P
=P0-
ρgh
P
=P0-
ρgh
2.
水银气压计中混入了一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768
mm
高的水银柱产生的压强时,这个水银气压计的读数只有
750
mm,此时管中的水银面到管顶的距离为
80
mm。当这个气压计的读数为740
mm水银柱时,实际的大气压相当于多高水银柱产生的压强?设温度保持不变。
二、平衡态下活塞、气缸密闭气体压强的计算
求用活塞封闭在静止容器内的气体压强,应对活塞进行受力分析。然后根据平衡条件求解。
S
m
⑧
m
S
⑦
练习:
气体对面的压力与面垂直:
F=PS
G
P0S
PS
PS
=
P0S+mg
G
PS
P0S′
N
S′
PS
=mg
+P0S'cosθ
PS
=
mg+P0S
M
m
S
⑨
M
m
S
⑩
以活塞为研究对象
以气缸为研究对象
mg+PS
=
P0S
Mg+PS
=
P0S
例2、如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住了一定质量的空气,而活塞与缸套间无摩擦,活塞面积为S,大气压强为P0,则下列说法正确的是(
)
A、内外空气对缸套的总作用力方向向上,大小为Mg
B、内外空气对缸套的总作用力方向向下,大小为mg
C、气缸内空气压强为P0-Mg/S
D、气缸内空气压强为P0+mg/S
AC
1.产生原因――碰撞
大量的气体对器壁的频繁撞击,产生一个均匀的,持续的压力(举例:雨伞),这个压力就产生了压强。
2.说明:压强与深度无关,在各处都相
等,向各个方向都有压强
3.单位:Pa
容器内气体压强
1
Pa=1
N/m2
求封闭气体的压强:
例1
方法总结:取研究对象
受力分析
列平衡式
求出气体压强
其实,生活中许多现象都表明,气体的压强,体积,温度三个状态量之间一定存在某种关系?究竟是什么关系呢?我们怎么来研究?
研究的方法-----控制变量法
本节课我们就来研究控制一定质量的某种气体,温度不变的情况下,压强与体积的变化关系。我们称之为等温变化
玻意耳定律:
一定质量的某种气体在温度不变的情况下,压强跟体积成反比.即pV=C(常量)或
p1V1=p2V2。
(1)成立条件:质量一定,温度不变,且压强不太大,温度不太低。
(2)pV=C。其中常量C?与气体的质量、温度有关。
p
V
0
气体等温变化的p-v图像
t1
t2
压强
(×105Pa)
0.3
0.6
0.9
1.2
1.5
体积
(h0×S)
16
8
5.3
4
3.2
图像:
o
p
P
O
V
(1)一定质量的某种气体在等温变化过程中压强p跟体积V的反比关系,在p-V
直角坐标系中表示出来的图线叫等温线。
等温线
P
O
V
(3)等温线的物理意义:图线上的一点表示气体的一个确定的状态。同一条等温线上各状态的温度相同,p与V
的乘积相同。不同温度下的等温线,离原点越远,温度越高。
(2)一定质量的气体等温线的p-V图是双曲线的一支。
一定质量气体的体积是5ml时,压强为1000Pa。当气体的体积减小3mL时,压强为多大?
前提是打气过程中温度保持不变,实际大气过程中,气体的温度升高
课后练习一:
某容器的容积是5L。里面所装的气体压强为1×106
Pa,温度不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?
课后变式1
课后练习二:
课后变式2
如图所示
水银柱的长度为19cm
大气压为1×10^5pa
相当于76cm高的水银柱产生的压强,玻璃管是粗细均匀的
玻璃管开口向上竖直放置时
被封闭的气柱长15cm
当开口竖直向下放置时水银没有溢出管口被封闭的气柱长度为多少?
容器内装有10×105Pa的气体5kg,
当放出一部分气体后,
容器内的气体压强减小到2×105Pa,
求容器中剩余气体的质量.
(设温度不变)
某种气体在状态A时的压强为2×105Pa体积为1m3,温度为200K。
(1)它经等温过程由状态A变为状态B,体积变为2m3。求状态B的压强。
(2)若经等容过程由状态B变为状态C,温度变为300K,求状态C的压强。
谢
谢
大
家
!
