2020-2021学年人教版八年级数学下册第十八章平行四边形重难点专项提升训练(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册第十八章平行四边形重难点专项提升训练(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 174.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-13 00:00:00 | ||
图片预览



文档简介
平行四边形重难点专项提升训练
一.选择题
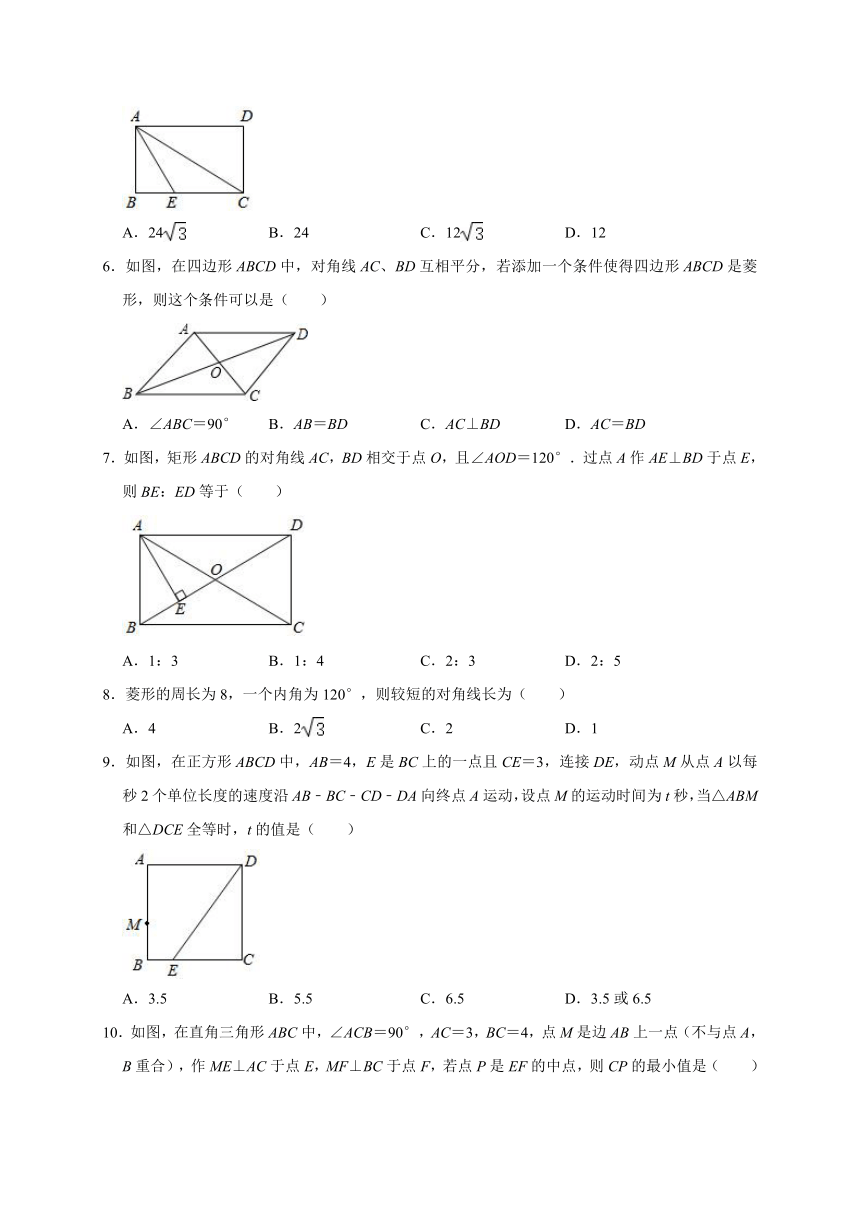
1.如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.65° C.100° D.130°
2.如图,在平行四边形ABCD中,N是CD的中点,AB=2BC,BN=m,AN=n,则CD的长为( )
A.+n B.m+ C. D.
3.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥AD,AO=CO
C.AB=AD,BC=CD D.AB∥CD,AD=BC
4.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
A.AD=3 B.AD=4 C.AD=5 D.AD=6
5.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
6.如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
7.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
8.菱形的周长为8,一个内角为120°,则较短的对角线长为( )
A.4 B.2 C.2 D.1
9.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
二.填空题
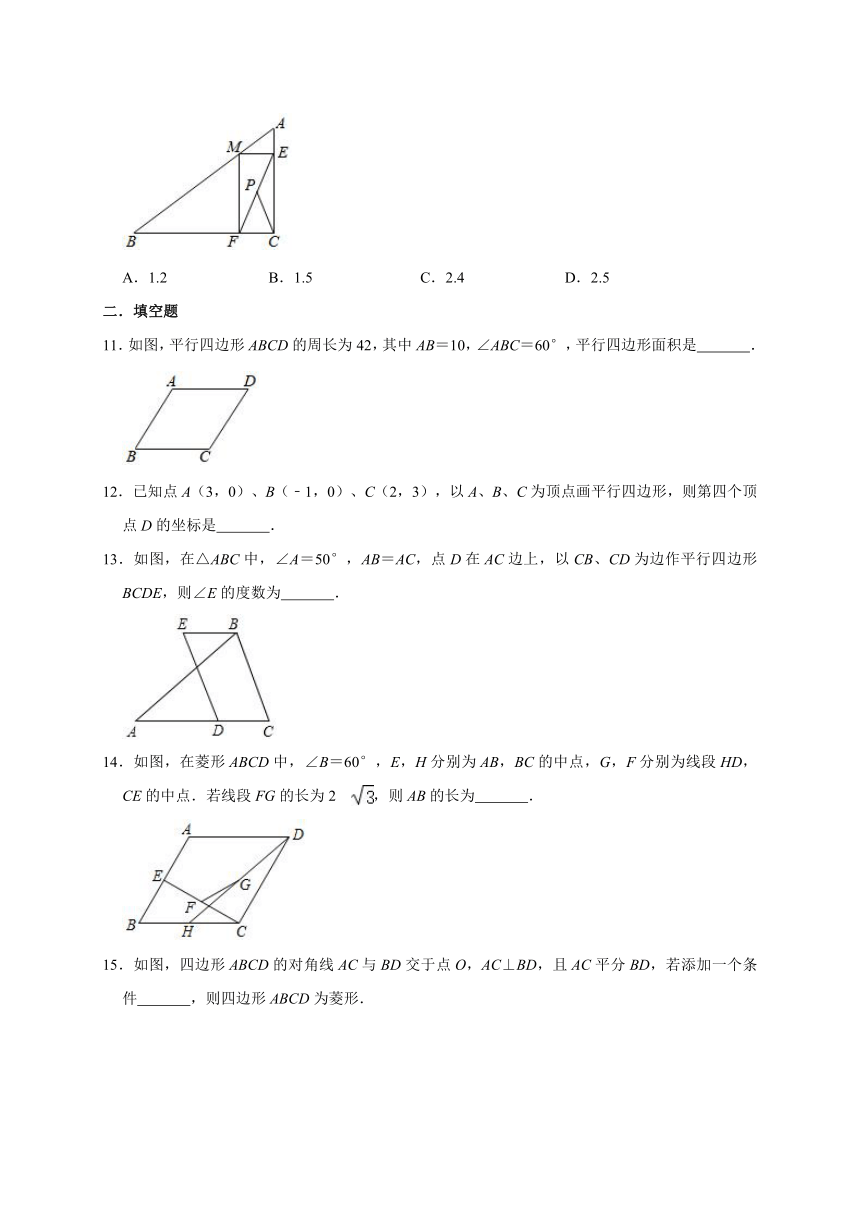
11.如图,平行四边形ABCD的周长为42,其中AB=10,∠ABC=60°,平行四边形面积是 .
12.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是 .
13.如图,在△ABC中,∠A=50°,AB=AC,点D在AC边上,以CB、CD为边作平行四边形BCDE,则∠E的度数为 .
14.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为 .
15.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
三.解答题
16.已知:如图,在?ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
17.如图所示,平行四边形ABCD,对角线BD平分∠ABC;
(1)求证:四边形ABCD为菱形;
(2)已知AE⊥BC于E,若CE=2BE=4,求BD.
18.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.
19.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且直线AB与DC之间的距离为4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,求AP的长度.
20.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:∠DAC=∠DCA;
(2)求证:四边形ABCD是菱形;
(3)若AB=,BD=2,求OE的长.
参考答案
一.选择题
1.解:在平行四边形ABCD中,∠B=∠D,AD∥BC,
∵∠B+∠D=100°,
∴∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故选:D.
2.解:∵N为CD中点,
∴CN=DN=CD=AB=BC=AD,
∴∠DAN=∠DNA,∠CBN=∠CNB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∴∠C=2∠DNA,∠D=2∠CNB,
∴∠DNA+∠CNB=(∠C+∠D)=90°,
∴∠ANB=180°﹣(∠DNA+∠CNB)=90°
即△NAB为直角三角形,
∵BN=m,AN=n,
∴CD=AB==.
故选:D.
3.解:能判定四边形ABCD是平行四边形的是∠A=∠C,∠B=∠D,理由如下:
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故选:A.
4.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD=10,∠C=∠D=90°,
∵M、N、E分别是PA、PB、AB的中点,
∴ME、NE是△ABP的中位线,
∴ME∥BP,NE∥AP,
∴四边形PMEN是平行四边形,
当∠APB=90°时,四边形PMEN是矩形,
设DP=x,CP=10﹣x,
由勾股定理得:AP2=AD2+x2,BP2=BC2+(10﹣x)2,AP2+BP2=AB2,
∴AD2+x2+AD2+(10﹣x)2=102,
AD2+x2﹣10x=0,
①当AD=3时,x2﹣10x+9=0,
x=1或x=9,符合题意;
②当AD=4时,x2﹣10x+16=0,
x=2或x=8,符合题意;
③当AD=5时,x2﹣10x+25=0,
x=5,符合题意;
④当AD=6时,x2﹣10x+36=0,无解;
故选:D.
5.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
6.解:添加一个条件为AC⊥BD,理由如下:
∵四边形ABCD中,对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴平行四边形ABCD是菱形.
故选:C.
7.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
8.解:如图,在菱形ABCD中,∠BAD=120°,
则∠B+∠BAD=180°,
∴∠B=60°,
∵菱形ABCD的周长为8,
∴AB=BC=CD=DA=2,
∴△ABC为等边三角形,
∴AC=AB=2,
故选:C.
9.解:如图,当点M在BC上时,
∵△ABM′和△DCE全等,
∴BM=CE,
由题意得:BM′=2t﹣4=3,
所以t=3.5(秒);
当点M在AD上时,
∵△ABM″和△CDE全等,
∴AM″=CE,
由题意得:AM″=16﹣2t=3,
解得t=6.5(秒).
所以,当t的值为3.5秒或6.5秒时.△ABM和△DCE全等.
故选:D.
10.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
二.填空题
11.解:如图,过点A作AE⊥BC于点E,
∵AB=10,∠ABC=60°,
∴BE=AB=5,
∴AE=BE=5,
平行四边形ABCD的周长为42,
∴AB+BC=21,
∴BC=21﹣10=11,
∴平行四边形面积是BC?AE=11×5=55.
故答案为:55.
12.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
13.解:在△ABC中,∠A=50°,AB=AC,
∴∠C=(180°﹣50°)÷2=65°,
∵四边形BCDE是平行四边形,
∴∠E=∠C=65°.
故答案为:65°.
14.解:如图,连接CG并延长,交AD于点M,连接EM,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,
∴∠A=120°,∠MGD=∠CGH,
∵点G为HD的中点,
∴HG=DG,
∵∠MGD=∠CGH,
∴△MGD≌△CGH(ASA),
∴MG=CG,MD=CH=BC=AD,
∴点G为MC的中点,点M为AD的中点,
∵F,G分别为CE和CM的中点,
∴FG是△CEM的中位线,
∴FG=EM,
∴EM=2FG=4,
∵E,M分别为AB和AD的中点,
∴AE=AM,
∵∠A=120°,
∴EM=AE=4,
∴AE=4,
∴AB=2AE=8.
故答案为:8.
15.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
三.解答题
16.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:连接AC,如图所示:
∵CE=2BE=4,
∴BE=2,
∴BC=BE+CE=6,
由(1)得:四边形ABCD是菱形,
∴AC⊥BD,AB=BC=6,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AE===4,
∴AC===4,
∵菱形ABCD的面积=AC×BD=BC×AE,
∴BD===4.
18.(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D是AB边的中点,
∴CD=AB=DA,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠ACB=90°,D是AB边的中点,
∴CD=AB=BD,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BDC=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
在Rt△CDF中,DF=CDsin60°=6×=3.
19.解:在平行四边形ABCD中,AB=CD,
∵BD=CD,
∴BD=BA,
又∵AM⊥BD,DN⊥AB,
∴DN=AM=4,
又∵∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,
∴∠P=∠PAM,
∴△APM是等腰直角三角形,
∴AP=AM=8.
20.(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,由勾股定理得:OA===2,
∴OE=OA=2.
一.选择题
1.如图,在平行四边形ABCD中,∠B+∠D=100°,则∠A等于( )
A.50° B.65° C.100° D.130°
2.如图,在平行四边形ABCD中,N是CD的中点,AB=2BC,BN=m,AN=n,则CD的长为( )
A.+n B.m+ C. D.
3.下列条件中能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D B.AB∥AD,AO=CO
C.AB=AD,BC=CD D.AB∥CD,AD=BC
4.如图,在矩形ABCD中,AB=10,P是CD边上一点,M、N、E分别是PA、PB、AB的中点,以下四种情况,哪一种四边形PMEN不可能为矩形( )
A.AD=3 B.AD=4 C.AD=5 D.AD=6
5.如图,矩形ABCD中,点E在BC上,且AE平分∠BAC,AE=CE,BE=2,则矩形ABCD的面积为( )
A.24 B.24 C.12 D.12
6.如图,在四边形ABCD中,对角线AC、BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是( )
A.∠ABC=90° B.AB=BD C.AC⊥BD D.AC=BD
7.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
8.菱形的周长为8,一个内角为120°,则较短的对角线长为( )
A.4 B.2 C.2 D.1
9.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
10.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
二.填空题
11.如图,平行四边形ABCD的周长为42,其中AB=10,∠ABC=60°,平行四边形面积是 .
12.已知点A(3,0)、B(﹣1,0)、C(2,3),以A、B、C为顶点画平行四边形,则第四个顶点D的坐标是 .
13.如图,在△ABC中,∠A=50°,AB=AC,点D在AC边上,以CB、CD为边作平行四边形BCDE,则∠E的度数为 .
14.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为 .
15.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
三.解答题
16.已知:如图,在?ABCD中,点E、F分别在AD、BC上,EF与BD相交于点O,AE=CF.求证:BD、EF互相平分.
17.如图所示,平行四边形ABCD,对角线BD平分∠ABC;
(1)求证:四边形ABCD为菱形;
(2)已知AE⊥BC于E,若CE=2BE=4,求BD.
18.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.
19.如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且直线AB与DC之间的距离为4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,求AP的长度.
20.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:∠DAC=∠DCA;
(2)求证:四边形ABCD是菱形;
(3)若AB=,BD=2,求OE的长.
参考答案
一.选择题
1.解:在平行四边形ABCD中,∠B=∠D,AD∥BC,
∵∠B+∠D=100°,
∴∠B=50°,
∴∠A=180°﹣∠B=180°﹣50°=130°.
故选:D.
2.解:∵N为CD中点,
∴CN=DN=CD=AB=BC=AD,
∴∠DAN=∠DNA,∠CBN=∠CNB,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠C+∠D=180°,
∴∠C=2∠DNA,∠D=2∠CNB,
∴∠DNA+∠CNB=(∠C+∠D)=90°,
∴∠ANB=180°﹣(∠DNA+∠CNB)=90°
即△NAB为直角三角形,
∵BN=m,AN=n,
∴CD=AB==.
故选:D.
3.解:能判定四边形ABCD是平行四边形的是∠A=∠C,∠B=∠D,理由如下:
∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形,
故选:A.
4.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD=10,∠C=∠D=90°,
∵M、N、E分别是PA、PB、AB的中点,
∴ME、NE是△ABP的中位线,
∴ME∥BP,NE∥AP,
∴四边形PMEN是平行四边形,
当∠APB=90°时,四边形PMEN是矩形,
设DP=x,CP=10﹣x,
由勾股定理得:AP2=AD2+x2,BP2=BC2+(10﹣x)2,AP2+BP2=AB2,
∴AD2+x2+AD2+(10﹣x)2=102,
AD2+x2﹣10x=0,
①当AD=3时,x2﹣10x+9=0,
x=1或x=9,符合题意;
②当AD=4时,x2﹣10x+16=0,
x=2或x=8,符合题意;
③当AD=5时,x2﹣10x+25=0,
x=5,符合题意;
④当AD=6时,x2﹣10x+36=0,无解;
故选:D.
5.解:∵四边形ABCD是矩形,
∴∠B=90°,
∴∠BAC+∠BCA=90°,
∵AE平分∠BAC,AE=CE,
∴∠BAE=∠EAC=∠ECA,
∴∠BAE+∠EAC+∠ECA=90°,
∴∠BAE=∠EAC=∠ECA=30°,
∴AE=CE=2BE=4,AB=2,
∴BC=BE+CE=6,
∴矩形ABCD面积=AB×BC=2×6=12;
故选:C.
6.解:添加一个条件为AC⊥BD,理由如下:
∵四边形ABCD中,对角线AC、BD互相平分,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴平行四边形ABCD是菱形.
故选:C.
7.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
8.解:如图,在菱形ABCD中,∠BAD=120°,
则∠B+∠BAD=180°,
∴∠B=60°,
∵菱形ABCD的周长为8,
∴AB=BC=CD=DA=2,
∴△ABC为等边三角形,
∴AC=AB=2,
故选:C.
9.解:如图,当点M在BC上时,
∵△ABM′和△DCE全等,
∴BM=CE,
由题意得:BM′=2t﹣4=3,
所以t=3.5(秒);
当点M在AD上时,
∵△ABM″和△CDE全等,
∴AM″=CE,
由题意得:AM″=16﹣2t=3,
解得t=6.5(秒).
所以,当t的值为3.5秒或6.5秒时.△ABM和△DCE全等.
故选:D.
10.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
二.填空题
11.解:如图,过点A作AE⊥BC于点E,
∵AB=10,∠ABC=60°,
∴BE=AB=5,
∴AE=BE=5,
平行四边形ABCD的周长为42,
∴AB+BC=21,
∴BC=21﹣10=11,
∴平行四边形面积是BC?AE=11×5=55.
故答案为:55.
12.解:如图,
以BC为对角线,将AB向上平移3个单位,再向左平移1个单位,B点对应的位置为(﹣2,3)就是第四个顶点D1;
以AB为对角线,将BC向下平移3个单位,再向右平移1个单位,B点对应的位置为(0,﹣3)就是第四个顶点D2′;
以AC为对角线,将AB向上平移3个单位,再向右平移4个单位,C点对应的位置为(7,3)就是第四个顶点D3;
∴第四个顶点D的坐标为:(﹣2,3)或(0,﹣3)或(7,3),
故答案为:(﹣2,3)或(0,﹣3)或(7,3).
13.解:在△ABC中,∠A=50°,AB=AC,
∴∠C=(180°﹣50°)÷2=65°,
∵四边形BCDE是平行四边形,
∴∠E=∠C=65°.
故答案为:65°.
14.解:如图,连接CG并延长,交AD于点M,连接EM,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,
∴∠A=120°,∠MGD=∠CGH,
∵点G为HD的中点,
∴HG=DG,
∵∠MGD=∠CGH,
∴△MGD≌△CGH(ASA),
∴MG=CG,MD=CH=BC=AD,
∴点G为MC的中点,点M为AD的中点,
∵F,G分别为CE和CM的中点,
∴FG是△CEM的中位线,
∴FG=EM,
∴EM=2FG=4,
∵E,M分别为AB和AD的中点,
∴AE=AM,
∵∠A=120°,
∴EM=AE=4,
∴AE=4,
∴AB=2AE=8.
故答案为:8.
15.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
三.解答题
16.证明:连接BE、DF,如图所示:
∵四边形ABCD为平行四边形,
∴AD=BC,AD∥BC,
又∵AE=CF,
∴DE=BF,
∴四边形EBFD为平行四边形,
∴BD、EF互相平分.
17.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD,
∴平行四边形ABCD是菱形;
(2)解:连接AC,如图所示:
∵CE=2BE=4,
∴BE=2,
∴BC=BE+CE=6,
由(1)得:四边形ABCD是菱形,
∴AC⊥BD,AB=BC=6,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴AE===4,
∴AC===4,
∵菱形ABCD的面积=AC×BD=BC×AE,
∴BD===4.
18.(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
∵∠ACB=90°,D是AB边的中点,
∴CD=AB=DA,
∴四边形ADCE为菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠ACB=90°,D是AB边的中点,
∴CD=AB=BD,
∵∠B=60°,
∴△BCD是等边三角形,
∴∠BDC=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
在Rt△CDF中,DF=CDsin60°=6×=3.
19.解:在平行四边形ABCD中,AB=CD,
∵BD=CD,
∴BD=BA,
又∵AM⊥BD,DN⊥AB,
∴DN=AM=4,
又∵∠ABD=∠MAP+∠PAB,∠ABD=∠P+∠BAP,
∴∠P=∠PAM,
∴△APM是等腰直角三角形,
∴AP=AM=8.
20.(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC平分∠BAD,
∴∠OAB=∠DAC,
∴∠DAC=∠DCA;
(2)证明:∵∠DAC=∠DCA,AB=AD,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
(3)解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,由勾股定理得:OA===2,
∴OE=OA=2.
