5.2平行线及其判定-2020-2021学年人教版七年级数学下册专题复习提升训练试卷(Word版含答案)
文档属性
| 名称 | 5.2平行线及其判定-2020-2021学年人教版七年级数学下册专题复习提升训练试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 552.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-14 15:07:01 | ||
图片预览



文档简介
专题复习提升训练卷5.2平行线及其判定-20-21人教版七年级数学下册
一、选择题
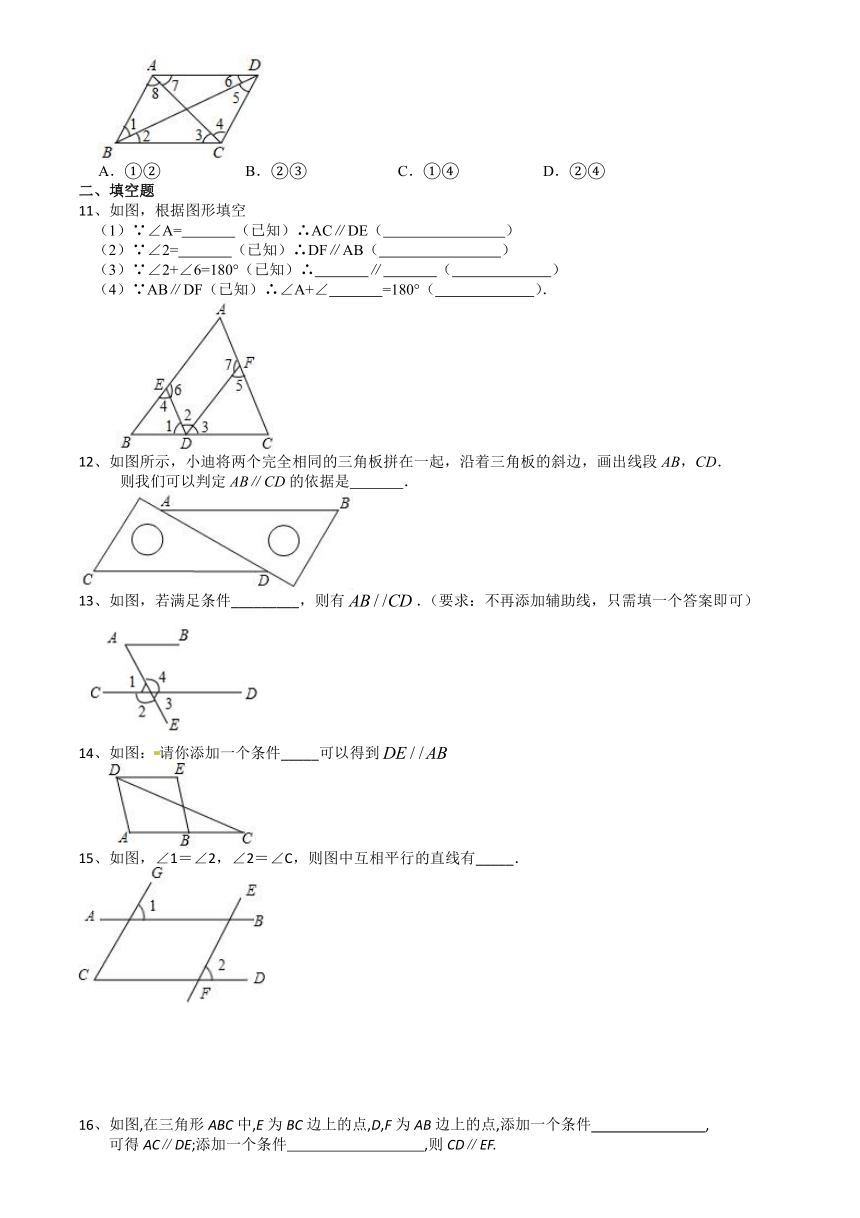
1、木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.以上结论都不正确
(2) (3)
2、如图,下列条件中不能判定AB∥CD的是( )
A.∠1+∠4=180° B.∠2=∠6 C.∠5+∠6=180° D.∠3=∠5
3、如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
4、如图,能判断AB∥CD的条件是( )
A.∠1=∠4 B.∠3=∠2 C.∠3=∠1 D.∠3=∠4
(5) (6)
5、如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4; (4)∠B=∠5.
A.1 B.2 C.3 D.4
6、如图所示,下列推理不正确的是( )
A.若∠1=∠B,则BC∥DE B.若∠2=∠ADE,则AD∥CE
C.若∠A+∠ADC=180°,则AB∥CD D.若∠B+∠BCD=180°,则BC∥DE
7、已知:如图,∠1=110°,∠2=70°,求证:a∥b.下面为嘉琪同学的证明过程:
解:∵∠1=110°,∠3=∠1(①), ∴∠3=110°,
又∵∠2=70°,∴∠2+∠3=180°, ∴a∥b(②).
其中①②为解题依据,则下列有关描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
(7) (8) (9)
8、一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,
则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
9、如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,
⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
10、如图,下列条件:①∠1=∠5;②∠2=∠6;⑧∠3=∠7;④∠4=∠8.其中能判定AB∥CD的是( )
A.①② B.②③ C.①④ D.②④
二、填空题
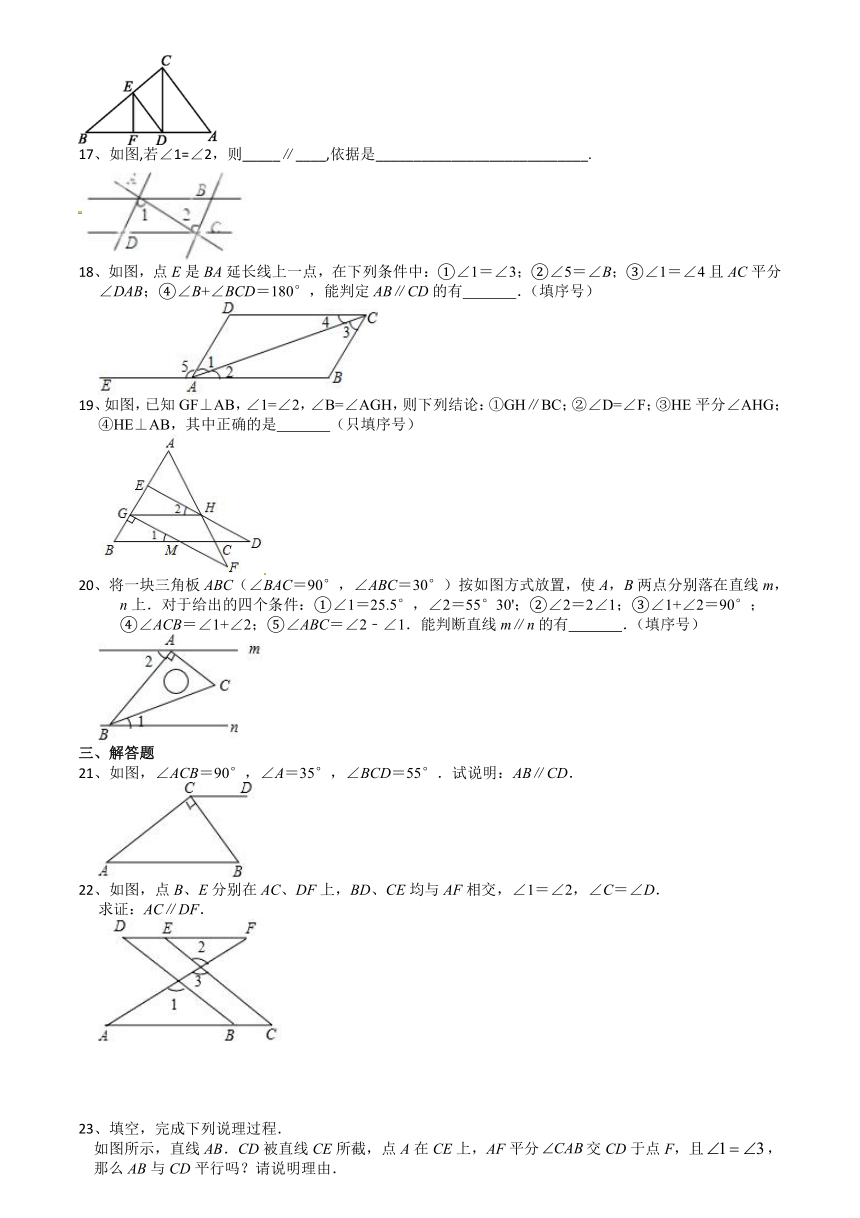
11、如图,根据图形填空
(1)∵∠A= (已知)∴AC∥DE( )
(2)∵∠2= (已知)∴DF∥AB( )
(3)∵∠2+∠6=180°(已知)∴ ∥ ( )
(4)∵AB∥DF(已知)∴∠A+∠ =180°( ).
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB,CD.
则我们可以判定AB∥CD的依据是 .
13、如图,若满足条件_________,则有.(要求:不再添加辅助线,只需填一个答案即可)
14、如图:请你添加一个条件_____可以得到
15、如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有_____.
16、如图,在三角形ABC中,E为BC边上的点,D,F为AB边上的点,添加一个条件 ,
可得AC∥DE;添加一个条件 ,则CD∥EF.?
17、如图,若∠1=∠2,则_____∥____,依据是____________________________.
18、如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
19、如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的是 (只填序号)
20、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,
n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
三、解答题
21、如图,∠ACB=90°,∠A=35°,∠BCD=55°.试说明:AB∥CD.
22、如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
23、填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________ ).
24、已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
25、已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
26、请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°. 求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________ (______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________ (______________________)
∴AB∥CD.( )
专题复习提升训练卷5.2平行线及其判定-20-21人教版七年级数学下册(答案)
一、选择题
1、木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.以上结论都不正确
解:木工师傅用图中的角尺画平行线,他依据的数学道理是同位角相等,两直线平行,
故选:A.
2、如图,下列条件中不能判定AB∥CD的是( )
A.∠1+∠4=180° B.∠2=∠6 C.∠5+∠6=180° D.∠3=∠5
【解答】解:A、∵∠1+∠4=180°,∠5+∠4=180°,∴∠1=∠5,∴AB∥CD,不符合题意;
B、∵∠2=∠4,∠2=∠6,∴∠4=∠6,∴AB∥CD,不符合题意
C、∵∠5+∠4=180°,∠5+∠6=180°,∴∠4=∠6,∴AB∥CD,不符合题意
D、对顶角相等,不能判定AB∥CD,符合题意.
故选:D.
3、如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
【解答】解:A、当∠ABD=∠FEC,无法判定AB∥EF,故选项错误;
B、当∠ABC=∠FEC时,AB∥EF,故选项正确;
C、当∠DBC=∠FEB时,无法判定AB∥EF,故选项错误;
D、当∠DBC=∠FEC时,BD∥EF,故选项错误.
故选:B.
4、如图,能判断AB∥CD的条件是( B )
A.∠1=∠4 B.∠3=∠2 C.∠3=∠1 D.∠3=∠4
5、如图,下列能判定AB∥CD的条件有( C )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4; (4)∠B=∠5.
A.1 B.2 C.3 D.4
6、如图所示,下列推理不正确的是( )
A.若∠1=∠B,则BC∥DE B.若∠2=∠ADE,则AD∥CE
C.若∠A+∠ADC=180°,则AB∥CD D.若∠B+∠BCD=180°,则BC∥DE
【解答】解:A、若∠1=∠B,则BC∥DE,不符合题意;
B、若∠2=∠ADE,则AD∥CE,不符合题意;
C、若∠A+∠ADC=180°,则AB∥CD,不符合题意;
D、若∠B+∠BCD=180°,则AB∥CD,符合题意.
故选:D.
7、已知:如图,∠1=110°,∠2=70°,求证:a∥b.下面为嘉琪同学的证明过程:
解:∵∠1=110°,∠3=∠1(①), ∴∠3=110°,
又∵∠2=70°,∴∠2+∠3=180°, ∴a∥b(②).
其中①②为解题依据,则下列有关描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
【解答】解:∵∠1=110°,∠3=∠1(对顶角相等),
∴∠3=110°,
又∵∠2=70°,
∴∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故选:C.
8、一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,
则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135°
C.30°和45° D.以上都有可能
解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故选:B.
9、如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,
⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
10、如图,下列条件:①∠1=∠5;②∠2=∠6;⑧∠3=∠7;④∠4=∠8.其中能判定AB∥CD的是( )
A.①② B.②③ C.①④ D.②④
解:①∵∠1=∠5,
∴AB∥CD,能判定AB∥CD;
②∵∠2=∠6,
∴AD∥BC,不能判定AB∥CD;
③∵∠3=∠7;
∴AD∥BC,不能判定AB∥CD;
④∵∠4=∠8,
∴AB∥CD,能判定AB∥CD.
故选:C.
二、填空题
11、如图,根据图形填空
(1)∵∠A= (已知)∴AC∥DE( )
(2)∵∠2= (已知)∴DF∥AB( )
(3)∵∠2+∠6=180°(已知)∴ ∥ ( )
(4)∵AB∥DF(已知)∴∠A+∠ =180°( ).
【解答】(1)∠4;同位角相等,两直线平行;(2)∠4;内错角相等,两直线平行;
(3)AB,DF,同旁内角互补,两直线平行;(4)7;两直线平行,同旁内角互补
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB,CD.
则我们可以判定AB∥CD的依据是 .
【解答】解:由题意:∠BAD=∠ADC=30°,
∴AB∥CD(内错角相等两直线平行),
故答案为内错角相等两直线平行.
13、如图,若满足条件_________,则有.(要求:不再添加辅助线,只需填一个答案即可)
答案:∠A=∠3(答案不唯一).
14、如图:请你添加一个条件_____可以得到
答案:答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,
都可以得到DE∥AB
15、如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有_____.
答案:EF∥CG,AB∥CD
16、如图,在三角形ABC中,E为BC边上的点,D,F为AB边上的点,添加一个条件 ,
可得AC∥DE;添加一个条件 ,则CD∥EF.?
本题两个空的答案均不唯一,如∠A=∠EDB ∠BFE=∠BDC
17、如图,若∠1=∠2,则_____∥____,依据是____________________________.
答案:AD BC 内错角相等,两直线平行
18、如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD (同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
19、如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的是 ①④ (只填序号)
20、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,
n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
三、解答题
21、如图,∠ACB=90°,∠A=35°,∠BCD=55°.试说明:AB∥CD.
【解答】解:∵∠ACB=90°,∠A=35°,
∴∠B=55°,
∵∠BCD=55°,
∴∠B=∠BCD,
∴CD∥AB.
22、如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
23、填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________ ).
解答:∵AF平分,
∴2(角平分线定义).
∵,
∴3(等量代换).
∴(内错角相等,两直线平行).
故答案为:2;角平分线定义;3;内错角相等,两直线平行.
24、已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
【解答】证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等),
∵∠1+∠2=180°(已知),
∴∠CGD+∠2=180°(等量代换),
∴AE∥FD(同旁内角互补,两直线平行),
∴∠A=∠BFD(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴∠BFD=∠D(等量代换),
∴AB∥CD(内错角相等,两直线平行).
25、已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
解答:证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
26、请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°. 求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________ (______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________ (______________________)
∴AB∥CD.( )
【解答】证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (角平分线的定义).
∵AE平分∠BAC (已知),
∴∠BAC=2∠β(角的平分线的定义).
∴∠ACD+∠BAC=2∠α+2∠β(等式性质).
即∠ACD+∠BAC=2(∠α+∠β).
∵∠α+∠β=90° (已知),
∴∠ACD+∠BAC=180° (等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:角平分线的定义,2∠β,等式性质,180°,等量代换,同旁内角互补,两直线平行
一、选择题
1、木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.以上结论都不正确
(2) (3)
2、如图,下列条件中不能判定AB∥CD的是( )
A.∠1+∠4=180° B.∠2=∠6 C.∠5+∠6=180° D.∠3=∠5
3、如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
4、如图,能判断AB∥CD的条件是( )
A.∠1=∠4 B.∠3=∠2 C.∠3=∠1 D.∠3=∠4
(5) (6)
5、如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4; (4)∠B=∠5.
A.1 B.2 C.3 D.4
6、如图所示,下列推理不正确的是( )
A.若∠1=∠B,则BC∥DE B.若∠2=∠ADE,则AD∥CE
C.若∠A+∠ADC=180°,则AB∥CD D.若∠B+∠BCD=180°,则BC∥DE
7、已知:如图,∠1=110°,∠2=70°,求证:a∥b.下面为嘉琪同学的证明过程:
解:∵∠1=110°,∠3=∠1(①), ∴∠3=110°,
又∵∠2=70°,∴∠2+∠3=180°, ∴a∥b(②).
其中①②为解题依据,则下列有关描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
(7) (8) (9)
8、一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,
则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135° C.30°和45° D.以上都有可能
9、如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,
⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
10、如图,下列条件:①∠1=∠5;②∠2=∠6;⑧∠3=∠7;④∠4=∠8.其中能判定AB∥CD的是( )
A.①② B.②③ C.①④ D.②④
二、填空题
11、如图,根据图形填空
(1)∵∠A= (已知)∴AC∥DE( )
(2)∵∠2= (已知)∴DF∥AB( )
(3)∵∠2+∠6=180°(已知)∴ ∥ ( )
(4)∵AB∥DF(已知)∴∠A+∠ =180°( ).
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB,CD.
则我们可以判定AB∥CD的依据是 .
13、如图,若满足条件_________,则有.(要求:不再添加辅助线,只需填一个答案即可)
14、如图:请你添加一个条件_____可以得到
15、如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有_____.
16、如图,在三角形ABC中,E为BC边上的点,D,F为AB边上的点,添加一个条件 ,
可得AC∥DE;添加一个条件 ,则CD∥EF.?
17、如图,若∠1=∠2,则_____∥____,依据是____________________________.
18、如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
19、如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的是 (只填序号)
20、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,
n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
三、解答题
21、如图,∠ACB=90°,∠A=35°,∠BCD=55°.试说明:AB∥CD.
22、如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
23、填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________ ).
24、已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
25、已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
26、请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°. 求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________ (______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________ (______________________)
∴AB∥CD.( )
专题复习提升训练卷5.2平行线及其判定-20-21人教版七年级数学下册(答案)
一、选择题
1、木工师傅用图中的角尺画平行线,他依据的数学道理是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.以上结论都不正确
解:木工师傅用图中的角尺画平行线,他依据的数学道理是同位角相等,两直线平行,
故选:A.
2、如图,下列条件中不能判定AB∥CD的是( )
A.∠1+∠4=180° B.∠2=∠6 C.∠5+∠6=180° D.∠3=∠5
【解答】解:A、∵∠1+∠4=180°,∠5+∠4=180°,∴∠1=∠5,∴AB∥CD,不符合题意;
B、∵∠2=∠4,∠2=∠6,∴∠4=∠6,∴AB∥CD,不符合题意
C、∵∠5+∠4=180°,∠5+∠6=180°,∴∠4=∠6,∴AB∥CD,不符合题意
D、对顶角相等,不能判定AB∥CD,符合题意.
故选:D.
3、如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC B.∠ABC=∠FEC C.∠DBC=∠FEB D.∠DBC=∠FEC
【解答】解:A、当∠ABD=∠FEC,无法判定AB∥EF,故选项错误;
B、当∠ABC=∠FEC时,AB∥EF,故选项正确;
C、当∠DBC=∠FEB时,无法判定AB∥EF,故选项错误;
D、当∠DBC=∠FEC时,BD∥EF,故选项错误.
故选:B.
4、如图,能判断AB∥CD的条件是( B )
A.∠1=∠4 B.∠3=∠2 C.∠3=∠1 D.∠3=∠4
5、如图,下列能判定AB∥CD的条件有( C )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4; (4)∠B=∠5.
A.1 B.2 C.3 D.4
6、如图所示,下列推理不正确的是( )
A.若∠1=∠B,则BC∥DE B.若∠2=∠ADE,则AD∥CE
C.若∠A+∠ADC=180°,则AB∥CD D.若∠B+∠BCD=180°,则BC∥DE
【解答】解:A、若∠1=∠B,则BC∥DE,不符合题意;
B、若∠2=∠ADE,则AD∥CE,不符合题意;
C、若∠A+∠ADC=180°,则AB∥CD,不符合题意;
D、若∠B+∠BCD=180°,则AB∥CD,符合题意.
故选:D.
7、已知:如图,∠1=110°,∠2=70°,求证:a∥b.下面为嘉琪同学的证明过程:
解:∵∠1=110°,∠3=∠1(①), ∴∠3=110°,
又∵∠2=70°,∴∠2+∠3=180°, ∴a∥b(②).
其中①②为解题依据,则下列有关描述正确的是( )
A.①代表内错角相等 B.②代表同位角相等,两直线平行
C.①代表对顶角相等 D.②代表同旁内角相等,两直线平行
【解答】解:∵∠1=110°,∠3=∠1(对顶角相等),
∴∠3=110°,
又∵∠2=70°,
∴∠2+∠3=180°,
∴a∥b(同旁内角互补,两直线平行).
故选:C.
8、一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,
则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为( )
A.60°和135° B.45°、60°、105°和135°
C.30°和45° D.以上都有可能
解:如图,
当AC∥DE时,∠BAD=∠DAE=45°;
当BC∥AD时,∠DAB=∠B=60°;
当BC∥AE时,∵∠EAB=∠B=60°,
∴∠BAD=∠DAE+∠EAB=45°+60°=105°;
当AB∥DE时,∵∠E=∠EAB=90°,
∴∠BAD=∠DAE+∠EAB=45°+90°=135°.
故选:B.
9、如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,
⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个 B.4个 C.5个 D.6个
解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
10、如图,下列条件:①∠1=∠5;②∠2=∠6;⑧∠3=∠7;④∠4=∠8.其中能判定AB∥CD的是( )
A.①② B.②③ C.①④ D.②④
解:①∵∠1=∠5,
∴AB∥CD,能判定AB∥CD;
②∵∠2=∠6,
∴AD∥BC,不能判定AB∥CD;
③∵∠3=∠7;
∴AD∥BC,不能判定AB∥CD;
④∵∠4=∠8,
∴AB∥CD,能判定AB∥CD.
故选:C.
二、填空题
11、如图,根据图形填空
(1)∵∠A= (已知)∴AC∥DE( )
(2)∵∠2= (已知)∴DF∥AB( )
(3)∵∠2+∠6=180°(已知)∴ ∥ ( )
(4)∵AB∥DF(已知)∴∠A+∠ =180°( ).
【解答】(1)∠4;同位角相等,两直线平行;(2)∠4;内错角相等,两直线平行;
(3)AB,DF,同旁内角互补,两直线平行;(4)7;两直线平行,同旁内角互补
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段AB,CD.
则我们可以判定AB∥CD的依据是 .
【解答】解:由题意:∠BAD=∠ADC=30°,
∴AB∥CD(内错角相等两直线平行),
故答案为内错角相等两直线平行.
13、如图,若满足条件_________,则有.(要求:不再添加辅助线,只需填一个答案即可)
答案:∠A=∠3(答案不唯一).
14、如图:请你添加一个条件_____可以得到
答案:答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,
都可以得到DE∥AB
15、如图,∠1=∠2,∠2=∠C,则图中互相平行的直线有_____.
答案:EF∥CG,AB∥CD
16、如图,在三角形ABC中,E为BC边上的点,D,F为AB边上的点,添加一个条件 ,
可得AC∥DE;添加一个条件 ,则CD∥EF.?
本题两个空的答案均不唯一,如∠A=∠EDB ∠BFE=∠BDC
17、如图,若∠1=∠2,则_____∥____,依据是____________________________.
答案:AD BC 内错角相等,两直线平行
18、如图,点E是BA延长线上一点,在下列条件中:①∠1=∠3;②∠5=∠B;③∠1=∠4且AC平分∠DAB;④∠B+∠BCD=180°,能判定AB∥CD的有 .(填序号)
解:①中,∵∠1=∠3,∴AD∥BC(内错角相等,两直线平行),不合题意;
②中,∵∠5=∠B,∴AD∥BC(同位角相等,两直线平行),不合题意;
③中,∵∠1=∠4且AC平分∠DAB,∴∠2=∠4,∴AB∥CD,故此选项符合题意;
④中,∠B+∠BCD=180°,∴AB∥CD (同旁内角互补,两直线平行),故此选项符合题意;
故答案为:③④.
19、如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的是 ①④ (只填序号)
20、将一块三角板ABC(∠BAC=90°,∠ABC=30°)按如图方式放置,使A,B两点分别落在直线m,
n上.对于给出的四个条件:①∠1=25.5°,∠2=55°30';②∠2=2∠1;③∠1+∠2=90°;
④∠ACB=∠1+∠2;⑤∠ABC=∠2﹣∠1.能判断直线m∥n的有 .(填序号)
解:①∵∠1=25.5°+∠ABC=55.5°=∠2=55°30',所以,m∥n;
②没有指明∠1的度数,当∠1≠30°,∠2≠∠1+30°,不能判断直线m∥n,故∠2=2∠1,不能判断直线m∥n;
③∠1+∠2=90°,不能判断直线m∥n;
④∠ACB=∠1+∠2,不能判断直线m∥n;
⑤∠ABC=∠2﹣∠1,判断直线m∥n;
故答案为:①⑤
三、解答题
21、如图,∠ACB=90°,∠A=35°,∠BCD=55°.试说明:AB∥CD.
【解答】解:∵∠ACB=90°,∠A=35°,
∴∠B=55°,
∵∠BCD=55°,
∴∠B=∠BCD,
∴CD∥AB.
22、如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D.
求证:AC∥DF.
证明:∵∠2=∠3,∠1=∠2,
∴∠1=∠3,
∴BD∥CE,
∴∠C=∠ABD;
又∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
23、填空,完成下列说理过程.
如图所示,直线AB.CD被直线CE所截,点A在CE上,AF平分交CD于点F,且,那么AB与CD平行吗?请说明理由.
解:∵AF平分,
∴________(_______________).
∵,∴__________(等量代换).
∴(________________ ).
解答:∵AF平分,
∴2(角平分线定义).
∵,
∴3(等量代换).
∴(内错角相等,两直线平行).
故答案为:2;角平分线定义;3;内错角相等,两直线平行.
24、已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
【解答】证明:∵∠1与∠CGD是对顶角,
∴∠1=∠CGD(对顶角相等),
∵∠1+∠2=180°(已知),
∴∠CGD+∠2=180°(等量代换),
∴AE∥FD(同旁内角互补,两直线平行),
∴∠A=∠BFD(两直线平行,同位角相等),
又∵∠A=∠D(已知),
∴∠BFD=∠D(等量代换),
∴AB∥CD(内错角相等,两直线平行).
25、已知,如图,∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,且∠1=∠3.求证:AB∥DC,请根据条件进行推理,得出结论,并在括号内注明理由.
证明:
∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.( )
∵∠ABC=∠ADC,( )
∴∠ =∠ (等量代换)
∵∠1=∠3( )
∴∠2=∠ .( )
∴ ∥ .( )
解答:证明:∵BF,DE分别平分∠ABC与∠ADC,(已知)
∴∠1=∠ABC,∠2=∠ADC.(角平分线的定义)
∵∠ABC=∠ADC,(已知)
∴∠1=∠2,(等量代换)
∵∠1=∠3,(已知)
∴∠2=∠3.(等量代换)
∴AB∥DC.(内错角相等,两直线平行)
故答案为:角平分线的定义;已知;1,2;已知;3,等量代换;AB,DC,内错角相等,两直线平行.
26、请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°. 求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________ (______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________ (______________________)
∴AB∥CD.( )
【解答】证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α (角平分线的定义).
∵AE平分∠BAC (已知),
∴∠BAC=2∠β(角的平分线的定义).
∴∠ACD+∠BAC=2∠α+2∠β(等式性质).
即∠ACD+∠BAC=2(∠α+∠β).
∵∠α+∠β=90° (已知),
∴∠ACD+∠BAC=180° (等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:角平分线的定义,2∠β,等式性质,180°,等量代换,同旁内角互补,两直线平行
